Աստիճան (հանրահաշիվ)
 Անվան այլ կիրառումների համար տե՛ս՝ Աստիճան (այլ կիրառումներ)
Անվան այլ կիրառումների համար տե՛ս՝ Աստիճան (այլ կիրառումներ)

Աստիճան, մաթեմատիկական գործողություն, գրվում է , որտեղ b թիվը հիմքն է իսկ n-ը՝ աստիճանացույցը կամ ցուցիչը։ Երբ n-ը դրական ամբողջ թիվ է, աստիճան բարձրացնելը համապատասխանում է հիմքի կրկնվող (n անգամ) բազմապատկմանը, այսինքն՝ թիվը հավասար է b հիմքի n արտադրյալին.
- ։
Ցուցիչը սովորաբար գրվում է հիմքի աջ վերտողում։ Այդ դեպքում արտահայտությունը կարդում են «b-ն բարձրացրած n աստիճանի» կամ «b-ի n աստիճան»։
Կամայական m և n դրական ամբողջ թվերի համար ճիշտ է նույնությունը։ Այս հատկությունը ոչ բնական ամբողջ ցուցիչների վրա տարածելու համար -ը սահմանում են 1 և -ը, որտեղ n-ը դրական ամբողջ թիվ է իսկ b-ն՝ զրոյից տարբեր կամայական թիվ, որպես ։ Մասնավորապես՝ հավասար է ։
Աստիճանի սահմանումը կարելի է ընդլայնել կամայական իրական կամ կոմպլեքս ցուցչի համար։ Ամբողջ ցուցիչով աստիճանը կարելի է սահմանել տարբեր հանրահաշվական կառույցների, այդ թվում մատրիցների համար։
Աստիճանը լայնորեն կիրառվում է տարբեր ոլորտներում, այդ թվում՝ տնտեսագիտություն, կենսաբանություն, քիմիա, ֆիզիկա և ինֆորմատիկա, այնպիսի կիրառություններով ինչպիսիք են՝ բարդ շահատոկոս, բնակչության աճ, քիմիական կինետիկա, ալիքների վարք և ծածկագիտություն։
Նշանակման պատմություն[խմբագրել | խմբագրել կոդը]
Հետևելով Հիպոկրատ Քիոսացուն[1]՝ հույն մաթեմատիկոս Էվկլիդեսը աստիճան եզրը օգտագործում էր հատվածի քառակուսու համար[2]։ Արքիմեդեսը բացահայտել և ապացուցել է ցուցիչների կանոնը, որը անհրաժեշտ է 10-ի աստիճանների հետ աշխատելու համար։ Պարսիկ մաթեմատիկոս Ալ-Խորեզմին 9-րդ դարում mal եզրը օգտագործում էր քառակուսու համար, իսկ kahb-ը՝ խորանարդի, ինչի պատճառով հետագայի (սկած 15-րդ դարից) իսլամական մաթեմատիկոսները դրանք համապատասխանաբար նշանակում էին m և k[3] տառերով։
16-րդ դարում Յոսթ Բուրգին ցուցիչների համար օգտագործում էր հռոմեական թվերը[4]։
17-րդ դարի սկզբին Ռենե Դեկարտն իր Երկրաչափություն աշխատության առաջին գրքում ներմուծել է աստիճանի ժամանակակից նշանակումը[5]։
Որոշ մաթեմատիկոսներ (օրինակ՝ Իսահակ Նյուտոնը) աստիճան օգտագործել են միայն երկուսից մեծ ցուցիչների համար՝ նախընտրելով թվի քառակուսին կրկնվող արտադրյալի տեսքով գրել։ Այսինքն, բազմանդամները նրանք գրում էին տեսքով։
1748 թվականին Լեոնարդ Էյլերը գրում է. «Պատկերացրեք աստիճանները, որտեղ ցուցիչը փոփոխական է։ Պարզ է, որ այս տեսակի մեծությունները հանրահաշվական ֆունկցիաներ չեն, քանի որ սրանցում ցուցիչը պետք է հաստատուն լինի»[6]։ Այսպիսով, Էյլերը ներկայացրեց տրանսցենդենտ ֆունկցիաները՝ հիմք դնելով բնական լոգարիթմի՝ որպես ցուցչային ֆունկցիայի հակադարձ ֆունկցիա ներմուծմանը (f(x) = ex)։
Ամբողջ ցուցիչներ[խմբագրել | խմբագրել կոդը]
Ամբողջ ցուցիչով աստիճանը կարելի է սահմանել տարրական թվաբանական գործողություններով։
Դրական ցուցիչ[խմբագրել | խմբագրել կոդը]
Դրական ամբողջ ցուցիչով աստիճանը կարելի է խիստ սահմանել միայն հետևյալ նախնական պայմանով[7]՝
և անդրադարձ առնչությամբ
- ։
Բազմապատկման զուգորդականությունից հետևում է, որ կամայական դրական ամբողջ m և n թվերի համար՝
- ։
Զրո ցուցիչ[խմբագրել | խմբագրել կոդը]
Զրոյից տարբեր կամայական թվի 0 աստիճանը հավասար է 1-ի[8].
- ։
Այս հատկության մեկնաբանություններից մեկը դատարկ արտադրյալն է։
00 արտահայտության արժեքի ընտրությունը կամ որևէ արժեք տալու հարցը կարող է կախված լինել համատեքստից
Բացասական ցուցիչ[խմբագրել | խմբագրել կոդը]
Հետևյալ նույնությունը ճիշտ է կամայական ամբողջ n և զրոյից տարբեր b թվերի համար՝
- ։
Զրոյի բացասական աստիճանը սահմանված չէ, բայց որոշ դեպքերում այն մեկնաբանվում է որպես անվերջություն (∞)։
Որպեսզի այս նույնությունը ստացվի բացասական թվերի համար ևս, զրոյից տարբեր b և դրական n թվի համար վերոհիշյալ անդրադարձ առնչությունը պետք է ձևափոխել հետևյալ կերպ՝
- ։
Ապա այս առնչությունը պետք է սահմանել ճիշտ բոլոր ամբողջ n և զրոյից տարբեր b թվերի համար, ինչից հետևում է, որ
Առհասարակ, զրոյից տարբեր կամայական b և ոչ բացասական ամբողջ n թվերի համար կունենանք՝
- ։
Նույնություններ և հատկություններ[խմբագրել | խմբագրել կոդը]
Հետևյալ նույնությունները ճիշտ են բոլոր ամբողջ ցուցիչների համար, եթե հիմքը տարբեր է զրոյից.
Ի տարբերություն գումարման և բազմապատկման՝
- Աստիճանը կոմուտատիվ չէ։ Օրինակ՝ ,
- Աստիճանը զուգորդական չէ։ Օրինակ՝ , բայց ։ Փակագծերի բացակայության դեպքում վերտողի նշանակման գործողության կարգը վերևից ներքև է (կամ «աջ» զուգորդական), ոչ թե ներքևից վերև[9][10][11][12] (կամ «ձախ» զուգորդական)։ Այսինքն,
որը, ընդհանուր առմամբ, տարբեր է
- -ից։
Գումարի աստիճան[խմբագրել | խմբագրել կոդը]
Գումարի աստիճանը սովորաբար կարելի է հաշվել Նյուտոնի երկանդամի միջոցով,
Սակայն, այս բանաձևը ճիշտ է միայն, երբ գումարելիները պատկանում են կոմուտատիվ հանրահաշվական կառույցի կամ առնվազն ։ Այլապես, օրինակ երբ -ն և -ն նույն չափի քառակուսի մատրիցներ են, այս բանաձևը չի կարող կիրառվել։ Սրանից հետևում է, որ հաշվողական հանրահաշվում ամբողջ ցուցիչների հետ կապ ունեցող շատ ալգորիթմներ պետք է փոփոխվեն, եթե հիմերը կոմուտատիվ չեն։ Հաշվողական հանրահաշվի որոշ ընդհանուր համակարգեր ոչ կոմուտատիվ հիմքով աստիճանի համար կիրառում են այլ նշանակում (հաճախ ^-ի փոխարեն ^^), որը կոչվում է ոչ կոմուտատիվ աստիճան։
Կոմբինատոր մեկնաբանում[խմբագրել | խմբագրել կոդը]
Ոչ բացասական ամբողջ n և m թվերի դեպքում արժեքը համապատասխանում է m տարր ունեցող բազմությունից դեպի n տարր ունեցող բազմություն գնացող ֆունկցիաների քանակին։ Նման ֆունկցիաները կարելի է ներկայացնել որպես m-շարաններ (կորտեժ) n տարր ունեցող բազմությունից (կամ m տառ ունեցող բառեր n տառ ունեցող այբուբենից)։ Հետևյալ աղյուսակում տրված է m և n թվերի որոշակի արժեքների օրինակներ.
nm Բոլոր m-շարանները {1, ..., n} բազմության տարրերից ոչինչ
Մասնավոր հիմքեր[խմբագրել | խմբագրել կոդը]
10-ի աստիճան[խմբագրել | խմբագրել կոդը]
Տասնորդական հաշվման համակարգերում 10-ի ամբողջ ցուցիչով աստիճանները գրվում են որպես 1, որին հետևում է կամ նախորդում է զրոներ՝ կախված ցուցչի նշանից և չափից։ Օրինակ՝ 103 = 1000 և 10−4 = 0.0001։
10 հիմքով աստիճանները օգտագործվում են գիտական նշանակման մեջ՝ չափազանց մեծ կամ չափազանց փոքր թվերը նշանակելու համար։ Օրինակ՝ (Լույսի արագությունը վակուումում), որը մոտարկվում է -ի։
Տասնորդական նախածանցները, որոնք նույնպես օգտագործվում են չափազանց փոքր կամ չափազանց մեծ թվերը նշանակելու համար, հիմնված են 10 հիմքով աստիճանների վրա։ Օրինակ՝ կիլոն նշանակում է 103 = 1000, հետևաբար մեկ կիլոմետրը հավասար է 1000 մետրի։
2-ի աստիճան[խմբագրել | խմբագրել կոդը]
Երկու հիմքով առաջին մի քանի բացասական աստիճանները լայնորեն կիրառվում են և ունեն հատուկ անուններ, օրինակ՝ կես և քառորդ։
Բազմությունների տեսությունում n տարր ունեցող բազմության բոլոր ենթաբազմությունների քանակը հավասար է 2n-ի։
Երկու հիմքով և ամբողջ ցուցիչով աստիճանները կարևոր նշանակություն ունեն ինֆորմատիկայում։ n-բիթ երկուական ամբողջ թվի բոլոր հնարավոր արժեքները հավասար է 2n. օրինակ՝ բայթը ընդունում է 28 = 256 տարբեր արժեք։ Հաշվարկման երկուական համակարգում կամայական թիվ արտահայտվում է 2-ի աստիճանների տեսքով, որը նշանակելու համար սովորաբար օգտագործվում է 0 և 1 թվերի հաջորդականություն և բինար կետ. կետից աջ գտնվող 1-երը դիտարկվում են որպես երկուսի բացասական աստիճան (ցուցիչը համընկնում է կետից հետո 1-ի դիրքի հետ), իսկ կետից ձախ գտնվող 1-երը՝ որպես երկուսի դրական աստիճան (ցուցիչը համընկնում է մեկի դիրքի հետ, որտեղ հաշվարկը սկսվում է զրոյից։ Թիվը հավասար է այս աստիճանների գումարին։ Օրինակ՝ 1101.101 թիվը հավասար է
1-ի աստիճան[խմբագրել | խմբագրել կոդը]
Մեկ հիմքով կամայական աստիճան հավասար է մեկի. 1n = 1։
0-ի աստիճան[խմբագրել | խմբագրել կոդը]
Դրական n ցուցիչի դեպքում (n > 0) զրոյի n աստիճանը հավասար է զրոյի. 0n = 0։
Բացասական n ցուցիչի դեպքում (n > 0) զրոյի n աստիճանը 0n որոշված չէ, քանի որ այն պետք է հավասար լինի -ի՝ ըստ սահմանման։
00 արտահայտությունը կամ սահմանվում է որպես 1, կամ չի սահմանվում (տե՛ս զրոյի զրո աստիճան)։
-1-ի աստիճան[խմբագրել | խմբագրել կոդը]
Զույգ n թվի դեպքում (−1)n = 1։
Կենտ n թվի դեպքում (−1)n = 1։
Այս հանգամանքը −1 թվի աստիճանները օգտակար է դարձնում նշանափոխ հաջորդականությունների նշանակման համար։
Մեծ ցուցիչներ[խմբագրել | խմբագրել կոդը]
Մեկից մեծ թվի աստիճանների հաջորդականության սահմանը տարամետ է, այլ կերպ ասած՝ հաջորդականությունն աճում է առանց սահման.
- , երբ , եթե ։
Սա կարելի է կարդալ որպես «b թվի n աստիճանը ձգտում է +∞-ի, երբ n-ը ձգտում է անվերջության, եթե b-ն մեծ է մեկից»։
Բացարձակ արժեքով մեկից փոքր թվի աստիճանը ձգտում է զրոյի, երբ ցուցիչը ձգտում է անվերջության.
- , երբ , եթե ։
Մեկի կամայական աստիճան հավասար է մեկի.
- կամայական n թվի համար, եթե ։
–1-ի աստիճանները փոխվում են 1 և –1 թվերի միջև, երբ n-ը փոխվում է կենտ և զույգ թվերի միջև, հետևաբար սահմանը գոյություն չունի, երբ n-ը ձգտում է անվերջության։
Եթե , -ը փոխվում է ավելի ու ավելի մեծ դրական և բացասական թվերի միջև, երբ n-ը փոխվում է կենտ և զույգ թվերի միջև (ձգտվելով անվերջության), հետևաբար այս սահմանը նույնպես գոյություն չունի։
Եթե հիմքը ձգտում է մեկի, իսկ ցուցիչը՝ անվերջության, վերևում նշված պայմանները միշտ չէ, որ գործում են։ Օրինակ՝
- , երբ ։
Այլ սահմանների, մասնավորապես անորոշ տեսք ունեցող սահմանների մասին ավելի ավելի մանրամասն նկարագրությունը #Աստիճանների սահմաններ բաժնում։
Աստիճանային ֆունկցիաներ[խմբագրել | խմբագրել կոդը]
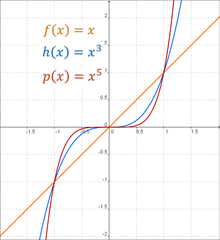

տեսքի իրական ֆունկցիաները, որտեղ , կոչվում են աստիճանային ֆունկցիաներ։ Եթե -ը ամբողջ թիվ է և , գոյություն ունեն երկու հիմնական ընտանիքներ. զույգ և կենտ -երի համար։ Ընդհանուր առմամբ, եթե և -ը զույգ է, ֆունկցիան կձգտի դրական անվերջության, երբ -ը ձգտի դրական կամ բացասական անվերջության։ Զույգ աստիճանային ֆունկցիաների գրաֆիկն ունի ֆունկցիայի գրաֆիկին նման տեսք[13]։ Նման համաչափություն ունեցող () ֆունկցիաները կոչվում են զույգ ֆունկցիաներ։
Կենտ ցուցիչի դեպքում ֆունկցիայի ասիմպտոտ վարքը փոխվում է կախված -ի նշանից։ Եթե , ֆունկցիան կձգտի դրական անվերջության, երբ -ը ձգտի դրական անվերջության, բայց երբ -ը ձգտում է բացասական անվերջության՝ ֆունկցիան ձգտում է բացասական անվերջության։ Կենտ աստիճանային ֆունկցիաների գրաֆիկն ունի ֆունկցիայի գրաֆիկին նման տեսք։ Նման համաչափություն () ունեցող ֆունկցիաները կոչվում են կենտ ֆունկցիաներ։
Երկու դեպքում էլ տեղի ունի հակառակ ասիմտոտ վարքը, երբ [13]։
Աստիճանների ցանկ[խմբագրել | խմբագրել կոդը]
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1,024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2,187 | 6,561 | 19,683 | 59,049 |
| 4 | 16 | 64 | 256 | 1,024 | 4,096 | 16,384 | 65,536 | 262,144 | 1,048,576 |
| 5 | 25 | 125 | 625 | 3,125 | 15,625 | 78,125 | 390,625 | 1,953,125 | 9,765,625 |
| 6 | 36 | 216 | 1,296 | 7,776 | 46,656 | 279,936 | 1,679,616 | 10,077,696 | 60,466,176 |
| 7 | 49 | 343 | 2,401 | 16,807 | 117,649 | 823,543 | 5,764,801 | 40,353,607 | 282,475,249 |
| 8 | 64 | 512 | 4,096 | 32,768 | 262,144 | 2,097,152 | 16,777,216 | 134,217,728 | 1,073,741,824 |
| 9 | 81 | 729 | 6,561 | 59,049 | 531,441 | 4,782,969 | 43,046,721 | 387,420,489 | 3,486,784,401 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | 1,000,000 | 10,000,000 | 100,000,000 | 1,000,000,000 | 10,000,000,000 |
Ռացիոնալ ցուցիչ[խմբագրել | խմբագրել կոդը]

Տրված b թվի n-րդ աստիճանի արմատը այն թիվն է, որը բավարարում է պայմանին։
Եթե b-ն դրական իրական թիվ է իսկ n-ը՝ դրական ամբողջ թիվ, արտահայտությունն ունի ճիշտ մեկ լուծում։
Այս լուծումը կոչվում է գլխավոր n-րդ արմատ b թվից։ Այն նշանակվում է -ով, որտեղ √ -ը կոչվում է արմատի նշան, գլխավոր արմատը նաև նշանակում են -ով։ Օրինակ՝ և ։
Այն փաստը, որ -ը լուծում է -ի համար կարելի է ապացուցել հետևյալ կերպ՝
Եթե n-ը զույգ է և b-ն՝ դրական, ուրեմն արտահայտությունն ունի երկու իրական լուծում, որոնք b-ի դրական և բացասական n-րդ արմատներն են, այսինքն՝ և ։
Եթե n-ը զույգ է և b-ն՝ բացասական, հավասարումը իրական լուծում չունի։
Եթե n-ը կենտ է, ուրեմն արտահայտությունն ունի ճիշտ մեկ լուծում, որը դրական է, եթե b-ն դրական է () և բացասական է, եթե b-ն բացասական է ()։
Դրական իրական b թիվը ռացիոնալ u/v աստիճան բարձրացնելով, որտեղ u-ն ամբողջ թիվ է իսկ v-ն՝ դրական ամբողջ թիվ, և միայն գլխավոր արմատները դիտարկելով ստացվում է՝
- ։
Բացասական իրական b թիվը ռացիոնալ u/v բարձրացնելիս, որտեղ u/v-ը չկրճատվող կոտորակ է, արդյունքում ստացվում է դրական իրական թիվ, եթե u-ն զույգ է (զույգ u-ից հետևում է, որ v-ն կենտ է, քանի որ u/v-ը չկրճատվող կոտորակ է ըստ սահմանման), որովհետև -ը դրական է, իսկ եթե u և v թվերը կենտ են, արդյունքում ստացվում է բացասական իրական թիվ, որովհետև -ն բացասական է։ Զույգ v (հետևաբար՝ կենտ u-ի) հնարավոր չէ դիտարկել այս ձևով, քանի որ գոյություն չունի իրական x թիվ, որը բավարարում է պայմանին։ Այս դեպքում -ի արժեքը նկարագրվում է կեղծ միավորով։
Այսպիսով, ունենք և ։ Չորս թիվը ունի երկու 3/2-րդ աստիճան. 8 և −8, սակայն, ընդունված է նշանակմամբ հասկանալ գլխավոր արմատը, հետևաբար՝ ։ u/v-րդ աստիճանը նաև կոչվում է v/u-րդ արմատ, իսկ զույգ v-ի դեպքում գլխավոր արմատ եզրը նաև վերաբերում է դրական արդյունքին։
Այս նշանային անորոշությունը պետք է հաշվի առնել աստիճանների նույնությունները կիրառելիս։ Օրինակ՝
- ,
որը ակնհայտորեն սխալ է։ Խնդիրը սկսվում է առաջին հավասարությունից՝ անորոշ իրավիճակում ստանդարտ նշանակում ներմուծելով (զույգ արմատ պահանջել) և պարզապես հիմնվելով միայն մեկ՝ ընդունված կամ գլխավոր մեկնաբանման վրա։ Նույն խնդիրբ առաջանում է անտեղի արմատի նշանը օգտագործելիս.
փոխարենը պետք է լինի՝
- ։
Նման խնդիրներ առաջանում են նաև կոմպլեքս թվերի դեպքում, ինչն ավելի մանրամասն նկարագրված է #Աստիճանային և լոգարիթմական նույնությունների ձախողում բաժնում։
Իրական ցուցիչ[խմբագրել | խմբագրել կոդը]
Դրական իրական թվերի իրական աստիճանը կարելի է սահմանել կամ իրական թվերի ռացիոնալ աստիճանի սահմանման ընդլայնմամբ, կամ այնպես, ինչպես նկարագրված է «Լոգարիթմներով աստիճան» բաժնում։ Արդյունքում միշտ ստացվում է դրական ամբողջ թիվ և պահպանվում են դրական իրական հիմքով և ամբողջ ցուցիչով աստիճանների նույնությունները և հատկությունները։
Մյուս կողմից, բացասական իրական թվի իրական աստիճան կայուն կերպով սահմանելը շատ ավելի դժվար է, քանի որ այն կարող է լինել ոչ իրական և ունենալ մեկից ավելի արժեքներ։ Հնարավոր է ընտրել այս արժեքներից մեկը՝ գլխավոր արժեքը, բայց գոյություն չունի գլխավոր արժեքի այնպիսի ընտրություն, որի դեպքում տեղի ունի հետևյալ առնչությունը (տես #Աստիճանային և լոգարիթմական նույնությունների ձախողում)՝
Հետևաբար՝ ոչ դրական իրական հիմքով աստիճանը հիմնականում դիտարկվում է որպես բազմարժեք ֆունկցիա։
Ռացիոնալ ցուցիչների սահմաններ[խմբագրել | խմբագրել կոդը]

Քանի որ կամայական իռացիոնալ թիվ կարելի է ներկայացնել ռացիոնալ թվերի հաջորդականության սահմանի տեսքով, դրական իրական b թվի կամայական իրական x աստիճանը կարելի է սահմանել անընդհատությամբ և հետևյալ կանոնով[14]՝
- ,
որտեղ r-ը մոտենում է x-ին՝ ընդունելով միայն ռացիոնալ արժեքներ։ Սահմանը գոյություն ունի միայն դրական b թվերի համար։ Այստեղ օգտագործվել է սահմանի (ε, δ) սահմանումը. այսինքն, ցույց է տրվել, որ տրված կամայական δ ճշգրտության դեպքում հնարավոր է ընտրել x-ի այնպիսի ε շրջակայք, որպեսզի այդ շրջակայքի բոլոր ռացիոնալ աստիճանները -ից տարբերվեն ամենաշատը տրված ճշգրտության չափ։
Օրինակ՝ եթե , կարելի է օգտագործել թվի ներկայացումը (հիմնվելով ռացիոնալ աստիճանների խիստ մոնոտոնության վրա)՝ ռացիոնալ թվերով սահմանափակված միջակայքեր գտնելու համար
- , , , , , , …
Սահմանափակված միջակայքերը զուգամիտում են ճիշտ մեկ իրական թվի, որը նշանակվում է -ով։ Նմանապես կարելի է ստանալ կամայական դրական իրական b թվի կամայական իռացիոնալ աստիճան։ Հետևաբար, ֆունկցիան սահմանված է բոլոր իրական x թվերի համար։
Ցուցչային ֆունկցիա[խմբագրել | խմբագրել կոդը]
Մաթեմատիկական հաստատուն e թիվը մոտավորապես հավասար է 2.718 և բնական լոգարիթմի հիմքն է։ Չնայած e թվի աստիճանը կարելի է դիտարկել այնպես, ինչպես կամայական իրական թվի աստիճանը, այն ունի բազմաթիվ օգտակար հատկություններ։ Այս հատկությունները թույլ են տալիս e-ի աստիճանները բնականորեն ընդլայնել այլ տեսակի աստիճանների վրա, ինչպես օրինակ՝ կոմպլեքս թվերը կամ մատրիցները։
Որպես հետևանք, արտահայտությամբ սովորաբար նշանակում են աստիճանի ընդհանրացված սահմանումը՝ ցուցչային ֆունկցիան (exp(x)), որը հնարավոր է սահմանել բազմաթիվ ձևերով, օրինակ՝
Այլ հատկություններից բացի, exp-ը նաև բավարարում է ցուցչային նույնությանը՝
- ։
Ցուցչային ֆունկցիան սահմանված է բոլոր ամբողջ, ռացիոնալ, իրական և կոմպլեքս թվերի համար։ Իրականում, ցուցչային մատրիցը սահմանված է քառակուսային մատրիցների համար (այս դեպքում ցուցչային նույնությանը ճիշտ է, երբ x-ը և y-ը կոմուտատիվ են) և օգտակար է գծային դիֆերենցիալ հավասարումների համակարգել լուծելու համար։
Քանի որ և -ը բավարարում է ցուցչային նույնությանը, հետևաբար -ը համընկնում է ամբողջ x-երի համար -ի սահմանմանը (կրկնվող բազմապատկում), ինչպես նաև այն, որ ռացիոնալ աստիճանները նշանակում են (դրական) արմատներ։ Այսպիսով, -ը համընկնում է նախորդ բաժնում իրական թվերի համար -ի սահմանմանը՝ ըստ անընդհատության։
Լոգարիթմներով աստիճան[խմբագրել | խմբագրել կոդը]
արտահայտությունը ցուցչային ֆունկցիա սահմանելու դեպքում -ը (կամայական դրական իրական b թվի դեպքում) կարելի է սահմանել -ի միջոցով։ Մասնավորապես, ln(x) բանական լոգարիթմը ցուցչային ֆունկցիայի հակադարձ ֆունկցիան է։ Այն սահմանված է դրական թվերի համար և բավարարում է հետևյալ պայմանին՝
- ։
Որպեսզի արտահայտությունը պահպանի ցուցիչների և լոգարիթմի կանոնները, այն կամայական իրական թվի համար պետք է բավարարի հետևյալ պայմանին՝
- ։
Սա կարող է օգտագործվել որպես իրական թվերի աստիճանի այլընտրանքային սահմանում, այն համապատասխանում է վերևում ռացիոնալ ցուցիչներով և անընդհանտությամբ տրված սահմանմանը։ Աստիճանի լոգարիթմներով սահմանում ավելի տարածված է կոմպլեքս թվերի համատեքստում։
Բացասական հիմքով իրական ցուցիչ[խմբագրել | խմբագրել կոդը]
Դրական իրական թվի աստիճանը միշտ դրական իրական թիվ է։ Չնայած հավասարումն ունի երկու լուծում՝ 2 և -2։ արտահայտության գլխավոր արժեքը 2–ն է, բայց -2-ը նույնպես թույլատրելի քառակուսի արմատ։ Եթե իրական թվերի աստիճանի սահմանումը ընդլայնվի բացասական արժեքների համար, ապա արդյունքը լավ վարք չի ունենա։
Լոգարիթմի կամ ռացիոնալ ցուցիչի մեթոդների միջոցով հնարավոր չէ արտահայտությունը սահմանել որպես իրական թիվ՝ բացասական իրական թվի և կամայական իրական թվի համար։ Քանի որ արտահայտությունը դրական է կամայական իրական թվի համար, ապա արտահայտությունն իրական թիվ չէ, երբ ։
Ռացինալ ցուցիչի մեթոդը չի կարող օգտագործվել բացասական արժեքների համար, քանի որ այն հիմնվում է անընդհատության վրա։ Կամայական թվի համար ֆունկցիան ունի ճիշտ մեկ[14] ընդլայնում ռացիոնալ թվերից դեպի իրական թվեր։ Բայց երբ , ֆունկցիան նույնիսկ անընդհատ չէ ռացիոնալ թվերի բազմության վրա։
Օրինակ՝ դիտարկենք դեպքը։ Կամայական բնական կենտ թվի դեպքում -1-ի n-րդ արմատը -1 է։ Այսպիսով, եթե -ը կենտ դրական ամբողջ թիվ է, ապա , եթե -ը զույգ է՝ ։ Հետևաբար, պայմանին բավարարող ռացիոնալ թվերի բազմությունը խիտ է ռացիոնալ թվերում, ինչպես նաև այն թվերի բազմությունը, որոնց համար տեղի ունի նույնությունը։ Սա նշանակում է, որ ֆունկցիան անընդհատ չէ կամայական ռացիոնալ թվի համար, որտեղ սահմանված է։
Մյուս կողմից, բացասական թվի կամայական կոմպլեքս աստիճան հնարավոր է սահմանել՝ ընտրելով -ի կոմպլեքս լոգարիթմ։
Իռացիոնալ ցուցիչ[խմբագրել | խմբագրել կոդը]
Եթե -ն դրական իրական հանրահաշվական թիվ է, իսկ -ը՝ ռացիոնալ, ապացուցված է, որ -ը հանրահաշվական թիվ է։ Այս պնդումը ճիշտ է նաև կամայական հանրահաշվական թվի դեպքում, միայն այն տարբերությամբ, որ -ը կարող է ընդունել մի քանի արժեք (վերջավոր թվով), որոնք բոլորը հանրահաշվական են։ Գելֆոնդ-Շնայդերի թեորեմը որոշ տեղեկություններ է տալիս իռացիոնալ -ի դեպքում -ի մասին, մասնավորապես՝
| Եթե -ն 0-ից և 1-ից տարբեր հանրահաշվական թիվ է և -ը իռացիոնալ հանրահաշվական թիվ է, ուրեմն արտահայտության բոլոր արժեքները (գոյություն ունեն անթիվ բազմությամբ արժեքներ) տրանսցենդենտ թվեր են (այսինքն՝ հանրահաշվական չեն)։ |
Կոմպլեքս ցուցիչ և դրական իրական հիմք[խմբագրել | խմբագրել կոդը]
Եթե -ն դրական իրական թիվ է իսկ -ը՝ կամայական կոմպլեքս թիվ, ուրեմն աստիճանը սահմանվում է հետևյալ կերպ՝
որտեղ -ը հավասարման միակ իրական լուծումն է, իսկ թվի կոմպլեքս աստիճանը սահմանված է ցուցչային ֆունկցիայով, որը կոմպլեքս փոփոխականով այն միակ ֆունկցիան է, որի ածանցյալը հավասար է իրեն և կետում ընդունում է 1 արժեքը։
Քանի որ -ը միշտ չէ, որ իրական թիվ է, տիպի արտահայտությունները չեն սահմանվում նախորդ սահմանմամբ։ Այն պետք է ներկայացվի կոմպլեքս թվերի աստիճանների կանոնների միջոցով, և եթե -ը իրական չէ կամ -ը ամբողջ չէ, այն ընդհանուր առմամբ հավասար չէ -ի։
Ցուցչային ֆունկցիան ունի բազմաթիվ սահմանումներ, բայց բոլորն էլ հաջողությամբ տարածվում են կոմպլեքս թվերի վրա և բավարարում են ցուցչային հատկությանը։ Կամայական կոմպլեքս և թվերի համար ցուցչային ֆունկցիան բավարարում է պայմանին։ Մասնավորապես, կամայական կոմպլեքս թվի համար
Արտահայտության երկրորդ արտադրյալը՝ -ը, կարելի է ներկայացնել Էյլերի բանաձևի միջոցով՝
- ։
Հետևաբար, կամայական կոմպլեքս թվի համար
- ։
Պյութագորասի եռանկյունաչափական նույնության հետևանքով արտահայտության բացարձակ արժեքը 1 է։ Հետևաբար, իրական արտադրյալը -ի բացարձակ արժեքն է իսկ ցուցիչի կեղծ մասը արտահայտում է կոմպլեքս թվի արգումենտը (աստիճանը)։
Շարքերով սահմանում[խմբագրել | խմբագրել կոդը]
Քանի որ ցուցչային ֆունկցիան հավասար է իր ածանցյալին և բավարարում է պայմանին, հետևաբար ֆունկցայի Թեյլորի շարքը կունենա հետևյալ տեսքը՝
- ։
Այս անվերջ շարքը, որը հաճախ ընդունվում է որպես կամայական կոմպլեքս ցուցիչի համար ֆունկցիայի սահմանում, բացարձակ զուգամիտում է կամայական կոմպլեքս թվի համար։
Եթե -ը ունի միայն կեղծ մաս, այսինքն՝ կամայական իրական -ի համար, շարքը վերածվում է հետևյալին՝
- ,
որը (բացարձակ զուգամիտության պատճառով) կարելի է վերադասավորել և ստանալ
- ։
Այս արտահայտության իրական և կոմպլեքս մասերը համապատասխանում են սինուսի և կոսինուսի Թեյլորի շարքերին (զրո կենտրոնով), որից հետևում է Էյլերի բանաձևը.
- ։
Սահմանով սահմանում[խմբագրել | խմբագրել կոդը]

Ցուցչային ֆունկցիան կարելի է նաև սահմանել որպես -ի սահման, երբ -ը ձգտում է անվերջության։ Այս սահմանման մեջ n-րդ աստիճանը ներկայացնելով որպես բևեռային տեսքով կրկնվող բազմապատկում՝ հնարավոր է վիզուալ ցույց տալ Էյլերի բանաձևը։ Կամայական կոմպլեքս թիվ կարելի է ներկայացնել բևեռային տեսքով, որտեղ -ը թվի բացարձակ արժեքն է, -ն՝ արգումենտը։ Երկու կոմպլեքս և թվերի արտադրյալը հավասար է -ի։
Կոմպլեքս հարթությունուն դիտարկենք այն ուղղանկյուն եռանկյունը, որի գագաթները 0, 1 և թվերն են։ -ի մեծ արժեքների դեպքում եռանկյունը գրեթե սեկտոր է՝ 1 շառավղով և ռադիան կենտրոնական անկյամբ։ -ը այդ դեպքում կարելի է մոտարկել բևեռային տեսքն ունեցող թվով։ Այսպիսով, երբ -ը ձգտում է անվերջության, -ը ձգտում է -ի՝ միավոր շրջանագծի այն կետրին, որի և դրական իրական առանցքի անկյունը կազմում է ռադիան։ Այս կետի Դեկարտյան կոորդինատներն են՝ , հետևաբար՝, որը Էյլերի բանաձևն է։
Պարբերականություն[խմբագրել | խմբագրել կոդը]
հավասարման լուծումները -ի ամբողջ արտադրյալներ են.
Հետևաբար, եթե -ն այնպիսի կոմպլեքս թիվ է, որ , ուրեմն -ին բավարարող կամայական կարելի է ստանալ -ից (-ին -ին բազմապատիկ որևէ թիվ գումարելով).
Այլ կերպ ասած, կամայական ամբողջ -ի համար կոմպլեքս ցուցիչային ֆունկցիան պարբերությամբ պարբերական ֆունկցիա է։
Օրինակներ[խմբագրել | խմբագրել կոդը]
Կոմպլեք թվերի աստիճան[խմբագրել | խմբագրել կոդը]
Զրոյից տարբեր կոմպլեքս թվերի ամբողջ ցուցիչով աստիճանները սահմանվում են կրկնվող բազմապատկման կամ բաժանման միջոցով։ Եթե -ը կեղծ միավորն է իսկ -ը՝ ամբողջ թիվ, ուրեմն արտահայտությունը հավասար է կամ ` կախված նրանից, թե -ը կոնգուրենտ է 0, 1, 2 կամ 3 թվերին (մոդ 4-ում)։ Այս պատճառով -ի ամբողջ աստիճանները օգտագործվում են 4 պարբերությաբ հաջորդականություններ նշանակելու համար։
Դրական իրական թվերի կոմպլեքս աստիճանները սահմանվում են ֆունկցիայի միջոցով՝ ինչպես նկարգրված է նախորդ «Կոմպլեքս ցուցիչ և դրական իրական հիմք» բաժնում։ Սրանք անընդհատ ֆունկցիաներ են։
Այս ֆունկցիաները կոմպլեքս թվի կամայական աստիճանի համար ընդհանրացնելիս առաջանում են որոշակի դժվարություններ. ֆունկցիաները ստացվում են կամ խզվող, կամ բազմարժեք են լինում։ Այս տարբերակներից ոչ մեկը բավարարող չէ։
Կոմպլեքս թվի ռացինոալ աստիճանը պետք է հանրահաշվական հավասարման լուծում լինի։ Հետևաբար, այն միշտ ունի վերջավոր թվով արժեքներ։ Օրինակ՝ -ը պետք է լինի հավասարման լուծում։ Բայց, եթե -ն լուծում է, ուրեմն լուծում է նաև -ն, քանի որ ։ Միակ, բայց ինչ-որ առումով կամայական լուծում, որը կոչում են գլխավոր արժեք, կարելի է ընտրել օգտվելով ինչ-որ ընդհանուր կանոնից։
Կոմպլեքս աստիճանները և լոգարիթմները ավելի բնականորեն մեկնաբանվում են որպես Ռիմանյան մակերևույթի վրա միարժեքանի ֆունկցիաներ։ Միարժեքանի ֆունկցիաները սահմանվում են ատլաս ընտրելով։ Արժեքը ունի խզում ճյուղավորման կտրվածքում։ Հնարավոր բազմաթիվ արժեքներից մեկն ընտրելով որպես հիմնական արժեք՝ ստացվում է ընդհատ ֆունկցիա և աստիճանների ծանոթ կանոնները կարող են սխալների հանգեցնել։
Կամայական կոմպլեքս թվի ոչ ռացիոնալ աստիճան ունի անթիվ բազմությամբ արժեքներ՝ կոմպլեքս լոգարիթմի բազմարժեքանիության պատճառով։ Սրանցից որպես գլխավոր արժեք ընտրվում է այն արժեքը, որի դեպքում դրական իրական և զրոյական կեղծ մասով կոմպլեքս թվերի աստիճանների արժեքները համընկնում են վերևի կանոնով սահմանված իրական հիմքով աստիճանների արժեքին։
Իրական թվի կոմպլեքս աստիճան բարձրացնելու գործողությունը ֆորմալ առումով տարբերվում է կոմպլեքս թիվի կոմպլեքս աստիճան բարձրացնելու գործողությունից։ Սակայն, դրական իրական թվերի դեպքում գլխավոր արժեքը նույնն է։
Բացասական իրական թվերի աստիճանները միշտ չէ, որ սահմանված են, իսկ սահմանված լինելու դեպքում խզվող են։ Ընդ որում, դրանք սահմանված են միայն այն դեպքում, երբ ցուցիչը ռացիոնալ թիվ է, որի հայտարարը կենտ ամբողջ թիվ է։
Կոմպլեքս ցուցիչ և կոմպլեք հիմք-կոպլեքսը այստեղ սխալ է գրված,խնդրում եմ ուշադիր լինել։[խմբագրել | խմբագրել կոդը]
Տրված և կոմպլեքս թվերի համար նշանակումը բազմիմաստ է այնպես, ինչպես արտահայտությունը։
-ին արժեք վերագրելու համար սկզբում ընտրում են -ի լոգարիթմի համար արժեք՝ : Այս ընտրությունը կարող է լինել գլխավոր արժեքը` (եթե այլ պայման տրված չէ) կամ կարող է լինել -ի այլ արժեք։ Օգտագործելով այս արժեքը և ցուցչային ֆունկցիան կարելի է սահմանել՝
- ,
քանի որ սա համընկնում է նախկին սահմանմանը, երբ -ն դրական իրական թիվ էր և օգտագործվում էր -ի (իրական) գլխավոր արժեքը։
Եթե -ը ամբողջ թիվ է, ուրեմն արտահայտության արժեքը կախված չէ -ի ընտրությունից և համընկնում է ամբողջ ցուցիչով աստիճանների նախկին սահմանմանը։
Եթե -ը տեսքի (չկրճատվող) ռացիոնալ թիվ է և , ուրեմն -ի հաշվելի քանակությամբ անվերջ արժեքները արտահայտության համար տալիս են արժեք։ Այս արժեքները հավասարման կոմպլեքս լուծումներն են։
Եթե -ը իռացիոնալ թիվ է, ուրեմն -ի հաշվելի քանակությամբ անվերջ արժեքները արտահայտության համար տալիս են անվերջ քանակությամբ իրարից տարբեր արժեքներ։
Կոմպլեքս աստիճանը հաշվելու համար օգտվում են դրա բևեռային տեսքից՝ ինչպես նկարագրված է նախորդ բաժնում։
Նման կառուցում օգտագործվում է նաև քվատերնիոնների համար։
Միավորի կոմպլեքս արմատներ[խմբագրել | խմբագրել կոդը]

Դրական ամբողջ թվերի համար պայմանին բավարարող կոմպլեքս թիվը կոչվում է միավորի n աստիճանի արմատ։ Երկրաչափորեն միավորի n աստիճանի արմատները կոմպլեքս հարթությունում գտնվում են միավոր շրջանագծին ներգծված այն n չափանի կանոնավոր բազմանկյան վրա, որի գագթներից մեկը գտնվում է 1 իրական թվի վրա։
Եթե , բայց պայմանին բավարարող բոլոր բնական թվերի համար , ուրեմն -ն կոչվում է միավորի n աստիճանի պարզունակ արմատ։ Բացասական մեկը միավորի միակ երկրորդ աստիճանի պարզունակ արմատն է։ Միավորի 4-րդ աստիճանի պարզունակ արմատներն են և ։
թիվը միավորի n աստիճանի ամենափոքր դրական արգումենտով պարզունակ արմատն է։ Այն երբեմն կոչվում է միավորի n աստիճանի գլխավոր արմատ, բայց այս եզրը համընդհանուր տարածում չունի և պետք չէ այն շփոթել -ի գլխավոր արժեքի հետ, որը հավասար է 1-ի[15]։
Միավորի n աստիճանի արմատները տրվում են հետևյալ կերպ՝
որտեղ ։
Կամայական կոմպլեքս թվի արմատներ[խմբագրել | խմբագրել կոդը]
Չնայած ընդհանուր կոմպլեքս լոգարիթմի համար կան անթիվ բազմությամբ արժեքներ, արտահայտությունը ունի վերջավոր արժեքներ, երբ , որտեղ -ը դրական ամբողջ թիվ է։ Սրանք թվի -րդ աստիճանի արմատներն են՝ հավասարման լուծումները։ Իրական արմատների նման 2-րդ աստիճանի արմատը կոչվում է քառակուսի արմատ, իսկ -րդ աստիճանի արմատը՝ խորանարդ արմատ։
Սովորաբար -ով նշանակում են արմատի գլխավոր արժեքը, որը ընդունում են -րդ աստիճանի այն արմատը, որի արգումենտը բացարձակ արժեքով ամենափոքրն է։ Երբ -ի կեղծ մասը զրո է իսկ իրական մասը դրական, այս սահմանումը համապատասխանում է իրական թվերի համար -ի ընդունված սահմանմանը։ Մյուս կողմից, երբ -ը կենտ ամբողջ թիվ է իսկ -ն՝ բացասական իրական թիվ, -ի արժեքը կախված է համատեքստից։
կոմպլեքս թվի -րդ աստիճանի արմատների բազմությունը կարելի է ստանալ գլխավոր արժեքը միավորից n-րդ աստիճանի արմատներով բազմապատկելով։ Օրինակ, 16-ի չորս արմատներն են՝ և , քանի որ 16-ի գլխավոր 4-րդ արմատը 2 է իսկ միավորի 4-րդ աստիճանի արմատները՝ և ։
Կոմպլեքս աստիճանի հաշվում[խմբագրել | խմբագրել կոդը]
Կոմպլեքս աստիճանները հաճախ ավելի հեշտ է հաշվել օգտվելով կոմպլեքս թվերի բևեռային ներկայացումից։ Կամայական կոմպլեքս թիվ հնարավոր է ներկայացնել բևեռային տեսքով հետևյալ կերպ՝
որտեղ -ը ոչ բացասական իրական թիվ է, իսկ -ն՝ -ի իրական արգումենտն է։ Բևեռային տեսքը ունի պարզ երկրաչափական մեկնաբանություն․ եթե կոմպլեքս թիվը ներկայացվի որպես կոմպլեքս հարթության կետ, որի Դեկարտյան կոորդինատը է, ապա -ը նույն կետի կոորդինատն է բևեռային կոորդինատներով։ Այսինքն, -ը «շառավիղն» է (), իսկ -ն՝ ակնյունը ()։ Բևեռային կոորդինատը միարժեք չէ, քանի որ -ին կարելի է գումարել -ի կամայական ամբողջ բազմապատիկ և ստանալ նույն կետը։ -ի յուրաքանչյուր ընտրություն տալիս է աստիճանի հավանական տարբեր արժեք։ Կոնկրետ արժեք ընտրելու համար կիրառվում է ճյուղավորման կտրվածք։ Գլխավոր արժեքը (ամենատարածված ճյուղավորման կտրվածքը) համապատասխանում է միջակայքից ընտրված -ի հետ։ Դրական իրական մաս և զրոյական կոմպլեքս մաս ունեցող կոմպլեքս թվերի դեպքում գլխավոր արժեքը համընկնում է իրական թվերի աստիճանի համապատասխան արժեքին։
կոմպլեքս աստիճանը հաշվելու համար նախ պետք է թիվը ներկայացնել բևեռային տեսքով՝
- ։
Հետո՝
հետևաբար՝
- ։
Եթե -ը ներկայացվում է տեսքով, ապա -ի բանաձևը կարելի է ավելի հստակորեն ներկայացնել հետևյալ տեսքով՝
- ։
Վերջնական բանաձևը հնարավորություն է տալիս կոմպլեքս աստիճանները հեշտությամբ հաշվել հիմքի բևեռային և ցուցիչի Դեկարտյան վերլուծումից։
Հետևյալ օրինակները օգտագործում են գլխավոր արժեքը՝ այն ճյուղային կտրվածքը, որի արդյունքում ։ թիվը հաշվելու համար նախ պետք է -ը ներկայացնել բևեռային և Դեկարտյան տեսքով՝
Հետևաբար նախորդ բանաձևի մեջ տեղադրելով և , կստացվի
- ։
Նմանապես -ի արժեքը գտնելու համար պետք է հաշվել -ի բևեռային տեսքը․
և տեղադրել ստացված բանաձևի մեջ
- ։
Կոմպլեքս աստիճանի արժեքը կախված է ընտրված ճյուղավորումից։ Օրինակ, եթե թիվը հաշվելու համար օգտագործվի բևեռային տեսքը, ապա արդյունքը կստացվի , մինչդեռ գլխավոր արժեքով ստացվել էր ։ արտահայտության բոլոր հնարավոր արժեքների բազմությունը տրվում է այսպես[16]՝
Այսպիսով, արտահայտությունն ունի անթիվ բազմության հնարավոր արժեքներ՝ յուրաքանչյուր ամբողջ թվի համար մեկ արժեք։ Այդ բոլոր արժեքները ունեն զրոյական կոմպլեքս մաս, հետևաբար կարելի է ասել, որ արտահայտությունը ունի անթիվ բազմությամբ ընդունելի իրական արժեքներ։
Աստիճանային և լոգարիթմական նույնությունների ձախողում[խմբագրել | խմբագրել կոդը]
Դրական իրական թվերի համար աշխատող որոշ աստիճանային և լոգարիթմական նույնություններ չեն աշխատում կոմպլեքս թվերի համար՝ անկախ նրանից, թե ինչպես է սահմանվում կոմպլեքս լոգարիթմը կամ կոմպլեքս աստիճանը որպես միարժեքանի ֆունկցիա։ Օրինակ՝
- նույնությունը ճիշտ է կամայական դրական իրական և իրական թվերի համար։ Բայց կոմպլեքս լոգարիթմի հիմնականում ճյուղի դեպքում ունենք՝
Անկախ նրանից թե լոգարիթմի որ ճղուղն է օգտագործվում, նույնության նմանատիպ ձախողում տեղի է ունենում։ Միայն այս արդյունքից ելնելով լավագույն դեպքում կարելի է պնդել, որ
Այս նույնությունը չի գործում նույնիսկ եթե լոգարիթմը դիտարկվի որպես բազմարժեք ֆունկցիա։ -ի արժեքները հանդիսանում են -ի հնարավոր արժեքների ենթաբազմություն։ -ի գլխավոր արժեքը նշանակելով և ենթադրելով, որ թվերը կամայական ամբողջ թիվ են, երկու կողմերի հնարավոր արժեքներն են՝
- և նույնությունները տեղի ունեն, երբ թվերը բնական իրական, իսկ -ը՝ իրական թվեր են։ Բայց հիմնական ճյուղերով հաշվարկները ցույց են տալիս, որ
և
Մյուս կողմից, երբ -ը ամբողջ թիվ է, նույնությունները տեղի ունեն բոլոր ոչզրոյական կոմպլեքս թվերի համար։
Եթե աստիճան բարձրացնելը համարենք բազմարժեք ֆունկցիա, ապա արտահայտության հնարավոր արժեքներն են ։ Նույնությունը գործում է, բայց չի կարելի ասել թե ։ - նույնությունը ճիշտ է կամայական իրական թվերի համար, բայց ենթադրությունը թե այն ճիշտ է կոմպլեքս թվերի համար, հանգեցնում է հետևյալ պարադոքսին, որը բացահայտել է Թոմաս Քլաուսենը 1827 թվականին[17]։
Կամայական ամբողջ թվի համար ունենք․
- (երկու կողմերը աստիճան բարձրացնելով)
- (ըստ նույնության)
- (ըստ նույնության)
- (բաժանելով -ի)
- ։
Ընդհանրացումներ[խմբագրել | խմբագրել կոդը]
Մոնոիդներ[խմբագրել | խմբագրել կոդը]
Ամբողջ ցուցիչով աստիճան բարձրացնելու գործողությունը կարելի է սահմանել կամայական բազմապատկական մոնոիդում[18]։ Մոնոիդը հանրահաշվական կառույց է՝ կազմված բազմությունից և դրա անդամների վրա սահմանված զուգորդական «բազմապատկման» գործողությամբ և ունի բազմապատկական նույնություն, որը նշանակում են 1-ով։ Աստիճան բարձրացնելու գործողությունը տրվում է հետևյալ ինդուկտիվ սահմանմամբ՝
- կամայական համար,
- կամայական և ոչ բացասական ամբողջ թվի համար,
- Եթե -ը բացասական է, ապա -ը սահմանված է միայն[19] այն դեպքում, երբ -ը ունի հակադարձ -ում։
Մոնոիդների մեջ են մտնում մաթեմատիկայի շատ կառույցներ, այդ թվում՝ խմբեր և օղակներ, որի ավելի մասնակի օրինակներից են մատրիցային օղակները և դաշտերը։
Մատրիցներ և գծային օպերատորներ[խմբագրել | խմբագրել կոդը]
Եթե -ն քառակուսի մատրից է, ապա -ն ինքն իր հետ անգամ բազմապատկման արդյունքը կոչվում է -ի աստիճան։ Ըստ սահմանման՝ -ը հավասար է միավոր մատրիցի[20], իսկ եթե -ն հակադարձելի է, ապա ։
Մատրիցների աստիճանները հաճախ կիրառվում են դիսկրետ դինամիկական համակարգերում, որտեղ մատրիցը արտահայտում է որոշակի համակարգի վիճակի վեկտորից համակարգի մեկ այլ՝ , վիճակին անցումը[21]։ Սա Մարկովի շղթայի ընդունված մեկնաբանությունն է։ Նմանապես, -ը համակարգի վիճակն է երկու քայլ հետո, ավելի ընդհանուր՝ -ը համակարգի վիճակն է քայլ հետո։ Այս դեպքում մատրիցը համակարգի ներկա վիճակից քայլ հետո եկող վիճակի անցման մատրիցն է։ Այսպիսով, մատրիցի աստիճան հաշվելը համարժեք է դինամիկական համակարգի էվոլյուցիայի լուծմանը։ Շատ դեպքերում մատրիցի աստիճանը հնարավոր է արագ հաշվել սեփական արժեքների և սեփական վեկտորների միջոցով։
Աստիճան բարձրացնելու գործողությունը կարելի է սահմանել ոչ միայն մատրիցների, այլև ավելի ընդհանուր գծային օպերատորների վրա։ Օրինակ՝ մաթեմատիկական անալիզի ածանցյալ օպերատորը, որը ֆունկցիայի վրա ազդող գծային օպերատոր է, ինչի արդյունքը՝ -ը, մեկ այլ ֆունկցիա է։ Ածանցման գործողության -րդ աստիճանը կարելի է սահմանել որպես ֆունկցիայի -րդ ածանցյալ․
- ։
Այս օրինակներում խոսվում է գծային օպերատորների դիսկրետ ցուցիչով աստիճանի մասին, բայց որոշ դեպքերում ցանկալի է նման օպերատորների վրա սահմանել նաև անընդհատ ցուցիչով աստիճանի հասկացությունը։ Սա կիսախմբերի մաթեմատիկական տեսության սկիզբն է[22]։ Ինչպես մատրիցի դիսկրետ ցուցիչով աստիճանի ստացումը լուծում է դիսկրետ դինամիկական համակարգերը, այնպես էլ մատրիցի անընդհատ ցուցիչով աստիճանի ստացումը լուծում է անընդհատ դինամիկայով համակարգերը։ Այս մեթոդներով լուծվում են Շրյոդինգերի հավասարումը, ալիքային հավասարումը և ժամանակից կախված այլ մասնակի դիֆերենցիալ հավասարումներ։ Ածանցյալի օպերատորը ոչ ամբողջ ցուցիչով աստիճան բարձրացնելը կոչվում է կոտորակային ածանցյալ, որը կոտորակային ինտեգրալի հետ միասին կոտորակային հաշվի հիմնական օպերատորներից է։
Վերջավոր դաշտեր[խմբագրել | խմբագրել կոդը]
Դաշտերը աբստրակտ կառույցներ են, որոնցում բազմապատկման, գումարման, հանման և բաժանման գործողությունները լավ սահմանված են և բավարարում են այդ գործողությունների ծանոթ հատկություններին։ Դաշտերի օրինակ են իրական թվերը, ռացիոնալ թվերը և կոմպլեքս թվերը։ Այս դաշտերը անվերջ բազմություններ են, սակայն գոյություն ունեն դաշտեր, որոնք ունեն վերջավոր տարրեր։ Օրինակ՝ երկու տարրից բաղկացած դաշտը, որտեղ գումարումը սահմանված է և ձևով, իսկ բազմապատկումը՝ և ։
Վերջավոր դաշտերում աստիճան բարձրացնելու գործողությունը կիրառվում է հանրային բանալու գաղտնագրությունում։ Օրինակ՝ Դիֆֆի-Հելլմանի բանալու փոխանակումն օգտագործում է այն փաստը, որ վերջավոր դաշտերում աստիճան բարձրացնելը հաշվելու առումով ավելի հեշտ է, մինչդեռ դիսկրետ լոգարիթմը (աստիճան բարձրացնելու հակադարձը) հաշվելու առումով դժվար է։
Կամայական վերջավոր դաշտում գոյություն ունի միակ պարզ թիվ, այնպես որ -ին պատկանող կամայական թվի համար , այսինքն՝ թիվը անգամ ինքն իրեն գումարելու դեպքում ստացվում է զրո։ Օրինակ՝ դաշտի դեպքում թիվը ունի այդ հատկությունը։ Այս պարզ թիվը կոչվում է դաշտի բնութագրող։ Ենթադրենք -ը բնութագրող թվով դաշտ է և դիտարկենք ֆունկցիան, որը -ի յուրաքանչյուր տարր բարձրացնում է աստիճան։ Սա կոչվում է դաշտի Ֆրոբենիուսի ավտոմատիզմ։ Այն դաշտի ավտոմորֆիզմ է առաջին կուրսեցու երազանք նույնության՝ -ի պատճառով։
Աբստրակտ հանրահաշիվ[խմբագրել | խմբագրել կոդը]
Աբստրակտ հանրահաշվում ամբողջ ցուցիչով աստիճանը կարելի է սահմանել բավական ընդհանուր կառույցների համար։
Եթե -ը բազմություն է, որի վրա սահմանված է աստիճանի ասոցիատիվությամբ բինար օպերատոր, ապա արտահայտությունը սահմանված է բազմության կամայական տարրի և զրոյից տարբեր կամայական բնական թվի համար հետևյալ կերպ՝
Այս դեպքում կունենանք հետևյալ հատկությունները՝
Եթե օպերատորը ունի երկկողմանի միավոր տարր 1, ապա արտահայտությունը կամայական -ի համար հավասար է 1-ի՝ ըստ սահմանման․[փա՞ստ]
Եթե բինար օպերատորը ունի երկկողմանի հակադարձ և ասոցիատիվ է, ապա խմբոիդը (մագման) խումբ է։ -ի հակադարձը նշանակում են -ով և այն դրա համար գործում են ցուցիչների բոլոր հայտնի կանոնները․
Եթե բազմապատկման գործողությունը կոմուտատիվ է (օրինակ՝ Աբելյան խմբերում), ապա ճիշտ է հետևյալ նույնությունը՝
- ։
Եթե բինար գործողությունը գրվում է գումարի տեսքով, ինչպես սովորաբար արվում է Աբելյան խմբերում, ապա «աստիճան բարձրացնելը կրկնվող բազմապատկում է» արտահայտությունը կարելի է վերաձևակերպել որպես «բազմապատկումը կրկնվող գումարում է»։ Այսպիսով, վերևում նշված աստիճանի յուրաքանչյուր օրենք ունի իր անալոգը բազմապատկման օրենքներում։
Երբ բազմության վրա սահմնաված են մի քանի աստիճանի ասոցիատիվությամբ բինար օպերատորներ, հաճախ կրկնվող օպերատորը նշելու համար վերտողային մասում ցուցիչից բացի նշում են նաև գործողության սիմվոլը։ Այսպիսով, -ը նույնն է ինչ կամ -ը նույնն է ինչ , որտեղ -ը համապատասխան բինար օպերատորների սիմվոլներն են։
Վերտողային նշանակումը նաև օգտագործվում է (հատկապես խմբերի տեսությունում) համալուծումը նշելու համար։ Այսինքն՝ , որտեղ -ն և -ը որոշոկի խմբի տարրեր են։ Չնայած համալուծումը ենթարկվում է աստիճանի որոշ օրենքներին, այն չի կարող ինչ-որ կերպով համարվել կրկնվող բազմապատկում։
Բազմությունների տեսություն[խմբագրել | խմբագրել կոդը]
Եթե -ը բնական թիվ է և -ն կամայական բազմություն, ապա արտահայտությամբ հաճախ նշանակում են բազմության տարրերի n չափանի շարանների (կորտեժ) բազմությունը։ Սա համարժեք է նրան, եթե -ով նշանակվի բազմությունից գնացող ֆունկցիաների բազմությունը․ շարանը համապատասխանում է այն ֆունկցիային, որը -ն արտապատկերում է -ին։
անվերջ կարդինալ թվի և բազմության համար նշանակումը կիրառվում է չափանի բազմությունից դեպի տանող ֆունկցիաների բազմությունը նշանակելու համար։ Սա հաճախ նշանակվում է κA ձևով՝ կարդինալ աստիճանից, որը սահմանվում է ներքևում, տարբերելու համար։
Այս ընդհանրացված աստիճանները կարելի է նաև սահմանել բազմությունների վրա արվող գործողությունների կամ հավելյալ կառույցներով բազմությունների համար։ Օրինակ՝ գծային հանրահաշվում իմաստ ունի ըստ կամայական ինդեքսների բազմությամբ ինդեքսավորել վեկտորական տարածությունների ուղիղ գումարները։ Այսինքն, կարող ենք խոսել
արտահայտության մասին, որտեղ -ը վեկտորական տարածություն է։
Եթե կամայական ինդեքսի համար , ապա արդյունքում ստացված ուղիղ գումարը կարելի է գրել կամ պարզապես (հասկանալով, որ խոսքն ուղիղ գումարի մասին է) տեսքով։ Այս դեպքում ևս կարելի է բազմությունը փոխարինել կարդինալ թվով՝ ստանալու համար, չնայած, առանց հզորությամբ բազմություն ընտրելու սա սահմանված է մինչև իզոմորֆություն։ Եթե -ն վերցնենք իրական թվերի դաշտը և -ը որևէ բնական թիվ, ապա կստանանք գծային հանարահշվում ամենահաճախ ուսումնասիրվող վեկտորական տարածությունը՝ -ը։
Եթե աստիճանի հիմքը բազմություն է, ապա աստիճան բարձրացնելու գործողությունը նույն Դեկարտյան արտադրյալն է, եթե այլ նշում չկա։ Քանի որ Դեկարտյան արտադրյալի արդյունքը n-շարաններ են, որոնք հնարավոր է ներկայացնել համապատասխան հզորությամբ բազմության վրա սահմանված ֆունկցիայով, հետևաբար -ը նույն է ինչ -ից տանող բոլոր ֆունկցիաների բազմությունը․
- ։
Սա համապատասխանում է կարդինալ թվերի աստիճանին այն իմաստով, որ , որտեղ -ը -ի հզորությունն է։ Երբ «2»-ը սահմանվում է որպես , ունենում ենք , որտեղ -ը (սովորաբար նշանակվում է -ով) բազմության բոլոր ենթաբազմությունների բազմությունն է․ բազմության կամայական ենթաբազմությանը միակորեն համապատասխանում է -ի վրա սահմանված ֆունկցիա, որը արժեքների դեպքում հավասար է 1-ի, այլապես՝ 0-ի։
Կատեգորիաների տեսություն[խմբագրել | խմբագրել կոդը]
Դեկարտյան փակ կատեգորիայում աստիճան բարձրացնելու գործողությունը կարող է օգտագործվել կամայական օբյեկտ այլ օբյեկտի աստիճան բարձրացնելու համար։ Սա ընդհանրացնում է բազմությունների կատեգորիայում Դեկարտյան արտադրյալը։ Եթե Դեկարտյան փակ կատեգորիայում 0-ն սկզբնական օբյեկտն է, ապա 00 ցուցչային օբյեկտը իզոմորֆ է կամայական 1 տերմինալ օբյեկտի։
Կարդինալ և օրդինալ թվերի աստիճան[խմբագրել | խմբագրել կոդը]
Բազմությունների տեսությունում գոյություն ունեն աստիճան բարձրացնելու գործողություններ կարդինալ և օրդինալ թվերի համար։
Եթե -ն և -ն կարդինալ թվեր են, ապա արտահայտությունը ներկայացնում է բոլոր այն ֆունկցիաների բազմության հզորությունը, որոնք սահմանված են հզորությամբ կամայական բազմության վրա և որոնց արժեքների բազմությունը ունի հզորություն[23]։ Եթե -ն և -ն վերջավոր են, ապա սա համապատասխանում է սովորական աստիճան բարձրացնելու գործողությանը։ Օրինակ՝ 2 տարր ունեցող բազմության անդամներից 3 չափանի շարանների բազմության հզորությունը է։ Կարդինալ թվաբանությունում արտահայտությունը միշտ 1-ի է հավասար (նույնիսկ եթե -ն զրո է կամ անվերջ կարդինալ)։
Կարդինալ թվերի աստիճանը տարբեր է օրդինալ թվերի աստիճանից, որը սահմանվում է տրանսֆինիտ ինդուկցիայի և սահմանի միջոցով։
Կրկնվող աստիճան բարձրացում[խմբագրել | խմբագրել կոդը]
Ինչպես բնական թվերի աստիճան բարձրացնելը մոտիվացված է կրկնվող բազմապատկմամբ, նմանապես հնարավոր է սահմանել գործողություն ըստ կրկնվող աստիճան բարձրացնելու․ այս գործողությունը հաճախ կոչվում է հիպեր-4 կամ տետրացիա։ Կրկնվող տետրացիայի գործողությամբ սահմանվում է մեկ այլ գործողություն, և այդպես շարունակ (տես՝ հիպերգործողություն)։ Գործողությունների այս հաջորդականությունը ներկայացվում է Ակերմանի ֆունկցիայի և Կնուտի վերսլաքային նշանակմամբ։ Ինչպես աստիճան բարձրացնելը աճում է ավելի արագ, քան բազմապատկումը, որն էլ իր հերթին աճում է ավելի արագ, քան գումարը, այդպես էլ տետրացիան աճում է ավելի արագ, քան աստիճան բարձրացնելը։ Այսպես, կետում գումարման, բազմապատկման, աստիճան բարձրացման և տետրացիա ֆունկցիաների արժեքները համապատասխանաբար հավասար են և ()-ի։
Աստիճանների սահմաններ[խմբագրել | խմբագրել կոդը]
Զրոյի զրո աստիճան () տեսքի սահմանները անորոշ են։ Այս օրինակներում սահմանը գոյություն ունի, բայց կարող է ունենալ տարբեր արժեքներ, ինչը ցույց է տալիս, որ երկու փոփոխականով ֆունկցիան սահման չունի կետում։
Այլ կետերում սահմանի գոյությունը ստուգելու համար ենթարդենք, որ սահմանված է բազմությունում։ Այս դեպքում -ն կարելի է համարել (բոլոր զույգերի բազմությունը, որտեղ -ը պատկանում են ընդլայնված թվային ուղղին) բազմության ենթաբազմություն, որը կպարունակի այն կետերը, որոնցում ֆունկցիան սահման ունի։
Ընդ որում, -ը -ի բոլոր կուտակման կետերում սահման ունի՝ բացառությամբ և կետերի[24]։ Հետևաբար, սա հնարավորություն է տալիս աստիճանը սահմանել ըստ անընդհատության, երբ ` բացառությամբ և -ի, որոնք մնում են անորոշ ձևեր։
Ըստ այս սահմանման՝
- և , երբ ,
- և , երբ ,
- և , երբ
- և , երբ ։
Այս աստիճանները ստացվել են -ի դրական արժեքների համար -ի սահմանը հաշվելու արդյունքում։ Այս մեթոդով չի սահմանվում -ը, երբ , քանի որ այդ դեպքում կետերը -ի կուտակման կետ չեն։
Մյուս կողմից, երբ -ը ամբողջ թիվ է, արժեքը արդեն իմաստ ունի -ի կամայական՝ այդ թվում բացասական արժեքների դեպքում։ Սա կարող է բացասական -երի համար վերևում սահմանված արտահայտությունը խնդրահարույց դարձնել կենտ -երի համար, քանի որ այս դեպքում , երբ -ը ձգտում է 0-ի դրական արժեքներով (աջից), բայց ոչ բացասական արժեքներով ձգտելու դեպքում (ձախից)։
Արդյունավետ հաշվում ամբողջ ցուցիչով[խմբագրել | խմբագրել կոդը]
Կրկնվող բազմապատկումների միջոցով -ը հաշվելու համար անհրաժեշտ է բազմապատկման գործողություն, սակայն այս արտահայտությունը կարելի է հաշվել ավելի արդյունավետ՝ ինչպես ցուցադրված է հետևյալ օրինակում։ արտահայտությունը հաշվելու համար կարելի է նկատել, որ ։ Այնուհետև հաշվել հետևյալ հերթականությամբ․
- :
Գործողությունների այս հաջորդականությունը պահանջում է միայն 8 բազմապատկման գործողություն (վերջին քայլում անհրաժեշտ է 2 բազմապատկում)՝ 99-ի փոխարեն։
Ընդհանուր առմամաբ արտահայտությունը հաշվելու համար անհրաժեշտ բազմապատկման գործողությունների քանակը կարելի է կրճատել մինչև Θ(log n)` աստիճան բարձրացնելու արագ ալգորիթմի կամ (ավելի ընդհանուր) գումարման շղթայով աստիճան բարձրացնելու ալգորիթմի միջոցով։ արտահայտությունը հաշվելու համար անհրաժեշտ նվազագույն բազմապատկման գործողությունների քանակը գտնելը դժվար խնդիր է, որի համար հայտնի արդյունավետ ալգորիթմ չկա (տես ենթաբազմության գումարի խնդիր), բայց գոյություն ունեն բազմաթիվ արդյունավետ էվրիստիկական ալգորիթմներ[25]։
Ֆունկցիաների անունների համար աստիճանային նշանակում[խմբագրել | խմբագրել կոդը]
Ֆունկցիայի անվան կամ սինվոլի վերտողում թիվ գրելը սովորաբար վերաբերում է ֆունկցիայի կոմպոզիցիային, ոչ թե կրկնվող բազմապատկմանը[26][27][28]։ Այսպիսով, սովորաբար նշանակում է [29], մասնավորապես՝ -ով սովորաբար նշանակում են -ի հակադարձ ֆունկցիան։ Այս նշանակումը ներմուծվել է Հանս Հայնրիխ Բյուրմանի[27][28] և Ջոն Ֆրեդերիկ Ուիլյամ Հերշելի[26][27][28] կողմից։ Իտերատիվ ֆունկցիաները կարևոր դեր ունեն ֆրակտալների և դինամիկ համակարգերի հետազոտությունում։ ֆունկցիոնալ քառակուսի արմատը գտնելու խնդիրը առաջին անգամ ուսումնասիրել է Չարլզ Բեբիջը։
Ֆունկցիայի կոմպոզիցիան և աստիճանը իրարից տարբերելու համար հաճախ աստիճան բարձրացնելու դեպքում ֆունկցիայի ցուցիչը գրում են փոփոխականի փակագծից հետո։ Այսինքն՝ -ը նշանակում է իսկ -ը՝ ։
Պատմական պատճառներով և հաշվի առնելով այն, որ փակագծերի բացթողման պատճառով անորոշություն է ստեղծվում՝ որոշակի եռանկյունաչափական և հիպերբոլական ֆունկցիաների անվան վերտողում գրվող թվերը հատուկ իմաստ ունեն․ ֆունկցիայի անվան վերտողում գրվող դրական ցուցիչը նշանակում է արդյունքը այդ աստիճան բարձրացնել[10][28][30][31][32][33][34][35][36], իսկ ցուցիչը շարունակում է նշանակել հակադարձ ֆունկցիան[28]։ Այսինքն՝ -ը պարզապես -ի կարճ գրելաձևն է[10][37][38][39][40][41][42][43], իսկ -ը սինուս ֆունկցիայի հակադարձն է՝ -ը։ Նման սովորույթ կա նաև լոգարիթմների գրառման ժամանակ[28], որտեղ -ը հաճախ նշանակում է ոչ թե [28]։
Երկիմաստությունից խուսափելու համար որոշ մաթեմատիկոսներ ֆունկցիայի կոմպոզիցիան նշանակում են -ով՝ ֆունկցիայի n-րդ իտերացիան նշանակելով, այսինքն՝ ։ Նույն խնդրի պատճառով Բենջամին Պիրցը օգտագործում էր նշանակումը[28][44], իսկ Ալֆրեդ Պրինգսհայմը և Ժյուլ Մոլքը առաջարկել են nf(x) նշանակումը[28][45][Ն 1]։
Ծրագրավորման լեզուներում[խմբագրել | խմբագրել կոդը]
Ծրագրավորման լեզուները սովորաբար աստիճանի գործողությունը ներկայացնում են միջածանցային օպերատորով կամ ֆունկցիայի տեսքով․
x ↑ y: Algol, Commodore BASIC, TRS-80 Level II/III BASIC[46][47]։x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (և իր ածանցյալ լեզուները), TI-BASIC, bc (ամբողջ ցուցիչների համար), Haskell (ոչ բացասական ցուցիչների համար), Lua և համակարգչային հանրահաշվական համակարգերի մեծ մասը։^սինվոլը նաև կիրառվում է որպես XOR POSIX Shell թվաբանական արտահայտություններում, AWK, C, C++, C#, D, Go, Java, JavaScript, Perl, PHP, Python, Ruby և Tcl լեզուներում, անուղղակիություն Pascal լեզվում և սինվոլային տողերի (string) միացում OCaml և Standard ML լեզուներում։x ^^ y: Haskell (կոտորակային հիմքի և ամբողջ ցուցիչի համար), D։x ** y: Ada, Z shell, Korn shell, Bash, Կոբոլ, CoffeeScript, Ֆորտրան, FoxPro, Gnuplot, Groovy, ՋավաՍկրիպտ, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, TCL, ABAP, Mercury, Haskell (սահող կետով ցուցիչների համար), Turing, VHDL.pown x y: F# (ամբողջ հիմքի և ամբողջ ցուցիչի համար).x⋆y: APL.
Շատ ծրագրավորման լեզուներ աստիճանի համար հատուկ նշանակում չունեն, բայց ունեն ֆունկցիա համապատասխան գրադարանում․
pow(x, y): C, C++.Math.Pow(x, y): C#.math:pow(X, Y): Erlang.Math.pow(x, y): Ջավա.[Math]::Pow(x, y): PowerShell.
Որոշ ցուցիչների համար գոյություն ունեն արտահայտությունը հաշվելու ավելի արագ եղանակներ։ Այս ցուցիչներից են՝ փոքր դրական կամ բացասական ամբողջ թվերը (-ը ավելի հեշտ է հաշվել, քան -ն, -ը ավելի հեշտ է, քան -ը) և քառակուսի արամատը (sqrt(x)-ը ավելի հեշտ է, քան -ը, cbrt(x) ավելի հեշտ է, քան -ը)։
Ոչ բոլոր ծրագրավորման լեզուներն են ենթարկվում գործողությունների կատարման նույն հերթականությանը․ չնայած Wolfram language-ը, Գուգլ որոնողական համակարգը և այլ լեզուներ գործողությունը կատարում են աջից ձախ (a^b^c-ը համարժեք է a^(b^c)-ի), շատ համակարգչային ծրագրեր (Microsoft Excel կամ Matlab) գործողությունները կատարում են ձախից աջ (a^b^c-ը համարժեք է (a^b)^c-ի)։
Նշումներ[խմբագրել | խմբագրել կոդը]
- ↑ Ֆունկցիայի համադրության նշանակման համար օգտագործվող Ալֆրեդ Պրինգսհայմի և Ժյուլ Մոլքի (1907) nf(x) նշանակումը պետք չէ շփոթել Ռուդոլֆ ֆոն Բիտեր Ռակերի (1982) nx նշանակման հետ, որը տետրացիան նշանակելու համար ներմուծվել է Հանս Մաուրերի (1901) և Ռուբեն Լուի Գուդշտեյնի կողմից։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Ball, Walter William Rouse (1888). A Short Account of the History of Mathematics (անգլերեն). Macmillan. էջ 36.
- ↑ O'Connor, John J.; Robertson, Edmund F., «Etymology of some common mathematical terms», MacTutor History of Mathematics archive, University of St Andrews.
- ↑ O'Connor, John J.; Robertson, Edmund F., «Abu'l Hasan ibn Ali al Qalasadi», MacTutor History of Mathematics archive, University of St Andrews.
- ↑ Cajori, Florian, 1859-1930. ([2007]). A history of mathematical notations,. New York, NY: Cosimo Classics. էջ 344. ISBN 978-1-60206-684-7. OCLC 707100737. Արխիվացված օրիգինալից 2021 թ․ ապրիլի 19-ին. Վերցված է 2020 թ․ օգոստոսի 5-ին.
{{cite book}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) CS1 սպաս․ թվային անուններ: authors list (link) - ↑ René Descartes, Discourse de la Méthode ... (Leiden, (Netherlands): Jan Maire, 1637), appended book: La Géométrie, book one, page 299. Արխիվացված 2017-10-08 Wayback Machine From page 299: " ... Et aa, ou a2, pour multiplier a par soy mesme; Et a3, pour le multiplier encore une fois par a, & ainsi a l'infini ; ... " ( ... and aa, or a2, in order to multiply a by itself; and a3, in order to multiply it once more by a, and thus to infinity ; ... )
- ↑ Euler, Leonhard (1748). Introductio in analysin infinitorum (Latin). Lausannae: M. M. Bousquet. էջ 75. OCLC 2684102.
{{cite book}}: CS1 սպաս․ չճանաչված լեզու (link) - ↑ Hodge, Jonathan K.; Schlicker, Steven; Sundstrom, Ted (2013 թ․ դեկտեմբերի 21). Abstract Algebra: An Inquiry Based Approach (անգլերեն). CRC Press. էջ 94. ISBN 978-1-4665-6706-1.
- ↑ Achatz, Thomas; Anderson, John G.; McKenzie, Kathleen (2005). Technical Shop Mathematics (անգլերեն) (3rd ed.). Industrial Press Inc. էջ 101. ISBN 978-0-8311-3086-2.
- ↑ Robinson, Raphael Mitchel (1958 թ․ հոկտեմբեր) [1958-04-07]. «A report on primes of the form k · 2n + 1 and on factors of Fermat numbers» (PDF). Proceedings of the American Mathematical Society (անգլերեն). Կալիֆոռնիայի համալսարան. 9 (5): 673–681 [677]. doi:10.1090/s0002-9939-1958-0096614-7. Արխիվացված (PDF) օրիգինալից 2020 թ․ հունիսի 28-ին. Վերցված է 2020 թ․ հունիսի 28-ին.
- ↑ 10,0 10,1 10,2 Bronstein, Ilja Nikolaevič; Semendjajew, Konstantin Adolfovič (1987) [1945]. «2.4.1.1. Definition arithmetischer Ausdrücke» [Definition of arithmetic expressions]. Written at Լայպցիգ. In Grosche, Günter; Ziegler, Viktor; Ziegler, Dorothea (eds.). Taschenbuch der Mathematik [Pocketbook of mathematics] (գերմաներեն). Vol. 1. Translated by Ziegler, Viktor. Weiß, Jürgen (23 ed.). Thun, Switzerland / Frankfurt am Main, Germany: Verlag Harri Deutsch (and B. G. Teubner Verlagsgesellschaft, Leipzig). էջեր 115–120, 802. ISBN 3-87144-492-8. «Regel 7: Ist F(A) Teilzeichenreihe eines arithmetischen Ausdrucks oder einer seiner Abkürzungen und F eine Funktionenkonstante und A eine Zahlenvariable oder Zahlenkonstante, so darf F A dafür geschrieben werden. [Darüber hinaus ist noch die Abkürzung Fn(A) für (F(A))n üblich. Dabei kann F sowohl Funktionenkonstante als auch Funktionenvariable sein.]»
- ↑ Olver, Frank W. J.; Lozier, Daniel W.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010). NIST Handbook of Mathematical Functions (անգլերեն). National Institute of Standards and Technology (NIST), U.S. Department of Commerce, Cambridge University Press. ISBN 978-0-521-19225-5. MR 2723248.[1] Արխիվացված 2013-07-03 archive.today
- ↑ Zeidler, Eberhard; Schwarz, Hans Rudolf; Hackbusch, Wolfgang; Luderer, Bernd; Blath, Jochen; Schied, Alexander; Dempe, Stephan; Wanka, Gert; Hromkovič, Juraj; Gottwald, Siegfried (2013) [2012]. Zeidler, Eberhard [in գերմաներեն] (ed.). Springer-Handbuch der Mathematik I (գերմաներեն). Vol. I (1 ed.). Berlin / Heidelberg, Germany: Springer Spektrum, Springer Fachmedien Wiesbaden. էջ 590. doi:10.1007/978-3-658-00285-5. ISBN 978-3-658-00284-8. 3-658-00284-0. (xii+635 pages)
- ↑ 13,0 13,1 Anton, Howard; Bivens, Irl; Davis, Stephen (2009 թ․ փետրվարի 14). Calculus Early Transcendentals 9th Edition Combined with Student Solutions Manual SV/MV 9th Edition and WileyPLUS Set (անգլերեն) (9th ed.). John Wiley & Sons, Incorporated. էջ 28. ISBN 978-0-470-50825-1. Արխիվացված օրիգինալից 2024 թ․ մարտի 15-ին. Վերցված է 2020 թ․ օգոստոսի 5-ին.
- ↑ 14,0 14,1 Denlinger, Charles (2011 թ․ հունվարի 28). Elements of Real Analysis (անգլերեն). Jones & Bartlett Learning. էջեր 278–283. ISBN 978-0-7637-7947-4. Արխիվացված օրիգինալից 2024 թ․ մարտի 15-ին. Վերցված է 2020 թ․ օգոստոսի 5-ին.
- ↑ Այս սահմանումը կարելի է գտնել հետևյալ գրքերում՝
- Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2001). Introduction to Algorithms (անգլերեն) (2 ed.). MIT Press. ISBN 978-0-262-03293-3. «Introduction to Algorithms» գրքի վերաբերյալ օնլայն նյութեր Արխիվացված 2007-09-30 Wayback Machine
- Paul Cull; Mary Flahive; Robby Robson (2005). Difference Equations: From Rabbits to Chaos (անգլերեն) (Undergraduate Texts in Mathematics ed.). Springer. ISBN 978-0-387-23234-8. Սահմանված է 351 էջում
- "Principal root of unity Արխիվացված 2020-08-05 Wayback Machine", MathWorld.
- ↑ Complex number to a complex power may be real Արխիվացված 2020-07-31 Wayback Machine at Cut The Knot gives some references to ii.
- ↑ Steiner J, Clausen T, Abel NH (1827). «Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen» [Problems and propositions, the former to solve, the later to prove]. Journal für die reine und angewandte Mathematik. 2: 286–287.(չաշխատող հղում)
- ↑ Nicolas Bourbaki (1970). Algèbre. Springer., I.2
- ↑ David M. Bloom (1979). Linear Algebra and Geometry. էջ 45. ISBN 978-0-521-29324-2.
- ↑ Chapter 1, Elementary Linear Algebra, 8E, Howard Anton
- ↑ Strang, Gilbert (1988), Linear algebra and its applications (3rd ed.), Brooks-Cole, Chapter 5.
- ↑ E Hille, R S Phillips: Functional Analysis and Semi-Groups. American Mathematical Society, 1975.
- ↑ Nicolas Bourbaki, Elements of Mathematics, Theory of Sets, Springer-Verlag, 2004, III.§3.5.
- ↑ Nicolas Bourbaki, Topologie générale, V.4.2.
- ↑ Gordon, D. M. (1998). «A Survey of Fast Exponentiation Methods» (PDF). Journal of Algorithms. 27: 129–146. CiteSeerX 10.1.1.17.7076. doi:10.1006/jagm.1997.0913. Արխիվացված է օրիգինալից (PDF) 2017 թ․ օգոստոսի 9-ին. Վերցված է 2020 թ․ օգոստոսի 2-ին.
- ↑ 26,0 26,1 Herschel, John Frederick William (1813) [1812-11-12]. «On a Remarkable Application of Cotes's Theorem». Philosophical Transactions of the Royal Society of London. Լոնդոն: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall. 103 (Part 1): 8–26 [10]. JSTOR 107384.
- ↑ 27,0 27,1 27,2 Herschel, John Frederick William (1820). «Part III. Section I. Examples of the Direct Method of Differences». A Collection of Examples of the Applications of the Calculus of Finite Differences (անգլերեն). Քեմբրիջ: Printed by J. Smith, sold by J. Deighton & sons. էջեր 1–13 [5–6]. Արխիվացված օրիգինալից 2020 թ․ օգոստոսի 4-ին. Վերցված է 2020 թ․ օգոստոսի 4-ին. [2] (NB. Այստեղ Հերշելը հղում է անում իր 1813 թվականի աշխատությանը և նշում է Հանս Հայնրիխ Բյուրմանի հին աշխատությունը։)
- ↑ 28,0 28,1 28,2 28,3 28,4 28,5 28,6 28,7 28,8 Cajori, Florian (1952) [March 1929]. «§472. The power of a logarithm / §473. Iterated logarithms / §533. John Herschel's notation for inverse functions / §535. Persistence of rival notations for inverse functions / §537. Powers of trigonometric functions». A History of Mathematical Notations (անգլերեն). Vol. 2 (3rd corrected printing of 1929 issue, 2nd ed.). Չիկագո: Open court publishing company. էջեր 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. 1-60206-714-7. Վերցված է 2016 թ․ հունվարի 18-ին. «[…] §473. Iterated logarithms […] We note here the symbolism used by Pringsheim and Molk in their joint Encyclopédie article: "2logb a = logb (logb a), …, k+1logb a = logb (klogb a)."[a] […] §533. John Herschel's notation for inverse functions, sin−1 x, tan−1 x, etc., was published by him in the Philosophical Transactions of London, for the year 1813. He says (p. 10): "This notation cos.−1 e must not be understood to signify 1/cos. e, but what is usually written thus, arc (cos.=e)." He admits that some authors use cos.m A for (cos. A)m, but he justifies his own notation by pointing out that since d2 x, Δ3 x, Σ2 x mean dd x, ΔΔΔ x, ΣΣ x, we ought to write sin.2 x for sin. sin. x, log.3 x for log. log. log. x. Just as we write d−n V=∫n V, we may write similarly sin.−1 x=arc (sin.=x), log.−1 x.=cx. Some years later Herschel explained that in 1813 he used fn(x), f−n(x), sin.−1 x, etc., "as he then supposed for the first time. The work of a German Analyst, Burmann, has, however, within these few months come to his knowledge, in which the same is explained at a considerably earlier date. He[Burmann], however, does not seem to have noticed the convenience of applying this idea to the inverse functions tan−1, etc., nor does he appear at all aware of the inverse calculus of functions to which it gives rise." Herschel adds, "The symmetry of this notation and above all the new and most extensive views it opens of the nature of analytical operations seem to authorize its universal adoption."[b] […] §535. Persistence of rival notations for inverse function.— […] The use of Herschel's notation underwent a slight change in Benjamin Peirce's books, to remove the chief objection to them; Peirce wrote: "cos[−1] x," "log[−1] x."[c] […] §537. Powers of trigonometric functions.—Three principal notations have been used to denote, say, the square of sin x, namely, (sin x)2, sin x2, sin2 x. The prevailing notation at present is sin2 x, though the first is least likely to be misinterpreted. In the case of sin2 x two interpretations suggest themselves; first, sin x · sin x; second,[d] sin (sin x). As functions of the last type do not ordinarily present themselves, the danger of misinterpretation is very much less than in case of log2 x, where log x · log x and log (log x) are of frequent occurrence in analysis. In his Introductio in analysin (1748), Euler[e] writes (cos. z)n, but in an article of 1754 he adopts sin ψ3 for (sin ψ)3 […] The parentheses as in (sin x)n were preferred by Karsten,[f] Carl Scherffer,[g] Paulli Frisii,[h] Abel (in some passages),[i] Ohm.[j] It passed into disuse during the nineteenth century. […] The designation sin x2 for (sin x)2 is found in the writings of Langrange, Johann Friedrich Lorenz, Lacroix, Gerhard Vieth, Stolz; it was recommended by Gauss. The notation sinn x for (sin x)n has been widely used and is now the prevailing one. It is found, for example, in Cagnoli,[k] DeMorgan,[l] Serret,[m] Todhunter,[n] Hobson,[o] Luis Octavio de Toledo,[p] Rothe.[q] […]» (xviii+367+1 pages including 1 addenda page) (NB. ISBN and link for reprint of 2nd edition by Cosimo, Inc., New York, USA, 2013.)
- ↑ Peano, Giuseppe (1903). Formulaire mathématique (ֆրանսերեն). Vol. IV. էջ 229.
- ↑ Cagnoli, Antonio (1786). Traité de Trigonométrie (ֆրանսերեն). Փարիզ: trad. par Chompré. էջ 20.
- ↑ De Morgan, Augustus (1849). Trigonometry and Double Algebra (անգլերեն). Լոնդոն. էջ 35.
- ↑ Serret, Joseph Alfred (1857). Traité de Trigonométrie (ֆրանսերեն) (2nd ed.). Փարիզ. էջ 12.
{{cite book}}: CS1 սպաս․ location missing publisher (link) - ↑ Todhunter, Isaac (1876). Plane Trigonometry (անգլերեն) (6th ed.). Լոնդոն. էջ 19.
{{cite book}}: CS1 սպաս․ location missing publisher (link) - ↑ Hobson, Ernest William (1911). Treatise on Plane Trigonometry (անգլերեն). Քեմբրիջ. էջ 19.
{{cite book}}: CS1 սպաս․ location missing publisher (link) - ↑ de Toledo, Luis Octavio (1917). Tradado de Trigonometria (իսպաներեն) (3rd ed.). Մադրիդ. էջ 64.
{{cite book}}: CS1 սպաս․ location missing publisher (link) - ↑ Rothe, Hermann (1921). Vorlesungen über höhere Mathematik (գերմաներեն). Վիեննա. էջ 261.
{{cite book}}: CS1 սպաս․ location missing publisher (link) - ↑ Euler, Leonhard (1748). Introductio in analysin infinitorum (լատիներեն). Vol. I. Լոզան: Marc-Michel Bousquet. էջեր 69, 98–99. Արխիվացված օրիգինալից 2023 թ․ մարտի 26-ին. Վերցված է 2020 թ․ օգոստոսի 5-ին. «Primum ergo considerandæ sunt quantitates exponentiales, seu Potestates, quarum Exponens ipse est quantitas variabilis. Perspicuum enim est hujusmodi quantitates ad Functiones algebraicas referri non posse, cum in his Exponentes non nisi constantes locum habeant.»
- ↑ Karsten, Wenceslaus Johann Gustav (1760). «Sectio XIII. De sectionibus angulorum et arcuum circularium». Mathesis theoretica Elementaris Atque Sublimior (լատիներեն). Ռոստոկ. էջ 511. Արխիվացված օրիգինալից 2021 թ․ ապրիլի 14-ին. Վերցված է 2020 թ․ օգոստոսի 4-ին. [3] Արխիվացված 2024-03-15 Wayback Machine
- ↑ Scherffer, Karl "Carolo" (1772). Institutionum analyticarum, pars secunda (լատիներեն). Վիեննա. էջ 144.
- ↑ Frisius (Frisii), Paulli (1782). Operum tomus primus (լատիներեն). Միլանո. էջ 303.
- ↑ Abel, Niels Henrik (1826). Journal für die reine und angewandte Mathematik (գերմաներեն). Բեռլին: August Leopold Crelle. I: 318–337;
{{cite journal}}: Missing or empty|title=(օգնություն) Abel, Niels Henrik (1827). Journal für die reine und angewandte Mathematik (գերմաներեն). Բեռլին: August Leopold Crelle. II: 26.{{cite journal}}: Missing or empty|title=(օգնություն) - ↑ Ohm, Martin (1829). System der Mathematik (գերմաներեն). Բեռլին. էջ 21. Part 3.
- ↑ Stibitz, George Robert; Larrivee, Jules A. (1957). Written at Անդրհիլ, Վերմոնտ. Mathematics and Computers (անգլերեն) (1 ed.). New York, USA / Toronto, Canada / London, UK: McGraw-Hill Book Company, Inc. էջ 169. LCCN 56-10331. (10+228 pages) (NB. Stibitz uses parentheses even in conjunction with trigonometric functions (like
(cos u)n) to avoid the ambiguity of thecosn unotation.) - ↑ Peirce, Benjamin (1852). Curves, Functions and Forces. Vol. I (new ed.). Բոստոն. էջ 203.
{{cite book}}: CS1 սպաս․ location missing publisher (link) - ↑ Pringsheim, Alfred; Molk, Jules (1907). Encyclopédie des sciences mathématiques pures et appliquées (ֆրանսերեն). Vol. I. էջ 195. Part I.
- ↑ Daneliuk, Timothy "Tim" A. (1982 թ․ օգոստոսի 9). «BASCOM - A BASIC compiler for TRS-80 I and II». InfoWorld. Software Reviews. Vol. 4, no. 31. Popular Computing, Inc. էջեր 41–42. Արխիվացված օրիգինալից 2020 թ․ փետրվարի 7-ին. Վերցված է 2020 թ․ փետրվարի 6-ին. «[…] If […] squaring is accomplished with TRS-80 BASIC's exponentiation (up-arrow) function, interpreter run time is 22 minutes 20 seconds, and compiled run time is 20 minutes 3 seconds. […]»
- ↑ «80 Contents». [80 Micro. 1001001, Inc. (45): 5. 1983 թ․ հոկտեմբեր. ISSN 0744-7868. Վերցված է 2020 թ․ փետրվարի 6-ին. «[…] The left bracket, [, replaces the up arrow used by RadioShack to indicate exponentiation on our printouts. When entering programs published in 80 Micro, you should make this change. […]» (NB. At code point 5Bh the TRS-80 character set has an up-arrow symbol "↑" in place of the ASCII left square bracket "[".)
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- «Բնական, ամբողջ և ռացիոնալ ցուցիչով աստիճան». mathnet.am. Վերցված է 2020 թ․ օգոստոսի 5-ին.
- «Մաթեմատիկա - Բնական ցուցիչով աստիճան». mathematics.am. Վերցված է 2020 թ․ օգոստոսի 5-ին., «Մաթեմատիկա - Աստիճանների բազմապատկումն ու բաժանումը». mathematics.am. Վերցված է 2020 թ․ օգոստոսի 5-ին.
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Աստիճան (հանրահաշիվ)» հոդվածին։ |
| ||||||
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի՝ 2020 թվականի 34-րդ շաբաթվա հոդված։ |
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 1, էջ 576)։ |

















![{\displaystyle {\begin{aligned}b^{0}&={\frac {b^{1}}{b}}=1,\\[3pt]b^{-1}&={\frac {b^{0}}{b}}={\frac {1}{b}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bed9de7b71c691c02f3c564384b12b7f682b5ba)


















































![{\displaystyle {\sqrt[{n}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a67075d2bf5949cd4927199b5ad24ee5d609b0)


![{\displaystyle 8^{1/3}={\sqrt[{3}]{8}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b98cc55d2011bf14ee68a5dfa848acba56cd11cd)





![{\displaystyle b^{\frac {u}{v}}=\left(b^{u}\right)^{\frac {1}{v}}={\sqrt[{v}]{b^{u}}}=\left(b^{\frac {1}{v}}\right)^{u}=\left({\sqrt[{v}]{b}}\right)^{u}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45e28cd344e3159d9f589601e68c6fd70fbe088d)









![{\displaystyle \left((-27)^{\frac {2}{3}}\right)^{\frac {3}{2}}={\sqrt {\left({\sqrt[{3}]{(-27)^{2}}}\right)^{3}}}={\sqrt {(-27)^{2}}}\neq -27}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7f4851c8fa70d183af2318007aed1fc1b379c86)
![{\displaystyle \left((-27)^{\frac {2}{3}}\right)^{\frac {3}{2}}=-{\sqrt {\left({\sqrt[{3}]{(-27)^{2}}}\right)^{3}}}=-{\sqrt {(-27)^{2}}}=-27}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9187340cbab3b7346e51a8b355a86c9a484d0dc9)







![{\displaystyle \left[b^{3},b^{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b5b00f7c93478b648fad3b5e3a6d4ae95f0cfb)
![{\displaystyle \left[b^{3.1},b^{3.2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81d4ad37b8a358c44af362b20baf8ba0810d867d)
![{\displaystyle \left[b^{3.14},b^{3.15}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42f6a21e3ae69576ed0997cc6857132b6de30f49)
![{\displaystyle \left[b^{3.141},b^{3.142}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10d55e590c2eef9cb6ce6aa156205c1139ac53c)
![{\displaystyle \left[b^{3.1415},b^{3.1416}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1140854a1f092dc1b4278fbf89e0baa178d0de4c)
![{\displaystyle \left[b^{3.14159},b^{3.14160}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5523df755c8e4ba0cceef84249c7e46e515dd5b5)








































































































![{\displaystyle {\sqrt[{n}]{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4953be5818fb650e16bd17b34af12e048950763a)
















![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)




![{\displaystyle (r^{c}e^{-d\theta })e^{i(d\ln(r)+c\theta )}=(r^{c}e^{-d\theta }){\big [}\cos {\big (}d\ln(r)+c\theta {\big )}+i\sin {\big (}d\ln(r)+c\theta {\big )}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274faaadca6b53c7a730f9783399c62413d2561c)
![{\displaystyle \theta \in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2742d923047f035ec3e8db8259485fda0629104b)




![{\displaystyle i^{i}=\left(1^{0}e^{-{\frac {1}{2}}\pi }\right)e^{i\left[1\cdot \ln(1)+0\cdot {\frac {1}{2}}\pi \right]}=e^{-{\frac {1}{2}}\pi }\approx 0.2079}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3039c472b0184a2f922cea31154f50026e2f041a)



![{\displaystyle (-2)^{3+4i}=(2^{3}e^{-4\pi })e^{i[4\ln(2)+3\pi ]}\approx (2.602-1.006i)\cdot 10^{-5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12664eac9b2e608c7b12c382b52daf8601d407d0)





![{\displaystyle i\pi =\log(-1)=\log \left[(-i)^{2}\right]\neq 2\log(-i)=2\left(-{\frac {i\pi }{2}}\right)=-i\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97f1c11016b556f60b416daa274f436bf70591f)





















































































































![{\displaystyle {\bar {\mathbb {R} }}=[-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39b9e613828cad5aff5748050d721c89cb1a3e53)
















































![{\displaystyle f^{[n]}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/161ebcd2965da8730384acffbcd46b7756469ac9)





