Մաթեմատիկական սոփեստություն

Մաթեմատիկական սոփեստություն (հուն․՝ σόφισμα՝ հնարք, խորամանկ հնարանք, գլուխկոտրուկ բառից^[1]), մաթեմատիկական սխալ պնդում՝ ստացված դատողության միջոցով, որը կարծես թե ճիշտ է, բայց իրականում պարունակում է այս կամ այն սխալը^[2]։ Սխալների պատճառները կարող են տարբեր լինել՝ մաթեմատիկայում արգելված գործողությունների օգտագործումը (օրինակ՝ բաժանում զրոյի վրա), մաթեմատիկական օրենքների ոչ ճիշտ օգտագործումը կամ դրանց կիրառելիության գոտուց դուրս օգտագործելը, տրամաբանական սխալները և այլն։

Մաթեմատիկական սոփեստությունը սոփեստության մասնավոր դեպքն է։ Տվյալ հոդվածում հետագայում խոսք է գնում միայն մաթեմատիկական սոփեստության մասին, որը կարճ անվանվել է սոփեստություն։ Սոփեստությունները չպետք է շփոթել գիտական պարադոքսների հետ (օրինակ՝ Զենոնի ապորիաների, ծննդյան օրերի պարադոքսի կամ Բանախ-Տարսկիի պարադոքսի հետ), որոնք սխալ չեն պարունակում և հաճախ ունենում են գիտական զգալի արժեք^[2]։

Սոփեստությունների վերլուծությունը, դրանցում սխալների որոնումը ծայրաստիճան արժեքավոր են մաթեմատիկայի դասավանդման ընթացքում, դրանք օգնում են աշակերտներին ու ուսանողներին ձևավորել մաթեմատիկական և տրամաբանական օրենքների հստակ պատկերացում, ինչպես նաև նախազգուշացնում են այս օրենքների կիրառման հնարավոր տիպային սխալները^[2]^[3]։

Պատմություն[խմբագրել | խմբագրել կոդը]

Պրոկլ Դիադոխոսը (մեր թվարկության 5-րդ դար) Էվկլիդեսի «Սկզբունքների» վերաբերյալ իր մեկնաբանություններում հայտնել է, որ Էվկլիդեսը դեռևս մեր թվարկությունից առաջ 3-րդ դարում երկրաչափություն ուսումնասիրողների համար կազմել է մաթեմատիկական սոփեստությունների ժողովածու, որն անվանել է «Պսևդարիա»։ Այն մեր օրեր չի հասել։ Սոփեստության նպատակը, ըստ Պրոկլի, սովորողներին դատողություններում սխալներ հայտնաբերել և հետագայում դրանցից խուսափել սովորեցնելն է^[3]։

Հետագայում՝ մինչև այժմ, գիտական գրականությունը, ինչպես նաև հետաքրքրաշարժ մաթեմատիկայի ժողովածուները, հաճախ ներառում են «գտնել սխալը» պահանջով սոփեստություններ, որոնց հիման վրա պարզաբանվում են մաթեմատիկական կանոնները և ստուգվում ընթերցողի գիտելիքները։

Սոփեստությունների դասակարգում[խմբագրել | խմբագրել կոդը]

Գոյություն ունի սոփեստությունների խմբավորման մի քանի տարբերակ. որոշ հեղինակներ դրանք խմբավորում են ըստ մաթեմատիկական թեմատիկայի տեսակի, մյուսները՝ ըստ դատողության մեջ թույլ տրված սխալի տիպի, իսկ երրորդները երկու մոտեցումները զուգակցում են այս կամ այն ձևով։

Ռուս մանկավարժ Վ. Ի. Օբրեիմովն առաջարկել է սոփեստությունները բաժանել ըստ սխալ արդյունքի տեսակի^[4].

անհավասարների հավասարություն,
հավասարների անհավասարություն,
ավեկի քիչը գերազանցում է ավելի շատին,
երկրաչափական անհամապատասխանություններ,
երևակայականն իրական է (սխալներ կոմպլեքս թվերի վերաբերյալ դատողություններում),
անլուծելի հավասարումներ։

Այս դասակարգումը քննադատվել է այն բանի համար, որ նույն սխալի վերաբերյալ նյութը միավորում է մաթեմատիկայի տարբեր բաժիններ, ինչը մեթոդաբանորեն սխալ է, և, ավելին, դասակարգման հատկանիշները բավարար չեն^[5]։

Գերմանացի մաթեմատիկոս Հերման Շուբերտը դիտարկել է սոփեստությունների չորս տեսակ («Մաթեմատիկական ժամանց և խաղեր», 1897)^[5].

բաժանում զրոյի վրա,
քառակուսի արմատի երկիմաստություն,
սխալներ երկրաչափական կառուցումներում,
անսահմանության հետ սխալ աշխատանք։

Տարրական մաթեմատիկա[խմբագրել | խմբագրել կոդը]

Հանրահաշիվ[խմբագրել | խմբագրել կոդը]

Բաժանում զրոյի վրա[խմբագրել | խմբագրել կոդը]

Սոփեստություն։ Դիցուք $a$ -ն և $b$ -ն կամայական թվեր են։ Նրանց տարբերությունը նշանակենք $c$ , տառով, այսինքն՝ $a-b=c$ : Այդ հավասարության երկու մասը բազմապատկենք $(a-b)$ -ով, կստանանք՝ $(a-b)^{2}=c(a-b)$ : Բացենք փակագծերը. $a^{2}-2ab+b^{2}=ca-cb$ : Հավասարության անդամները խմբավորենք հետևյալ կերպ. $a^{2}-ab-ac=ab-b^{2}-bc,$ կամ՝

a(a-b-c)=b(a-b-c):

Երկու մասը կրճատենք $(a-b-c)$ -ով, կստանանք. $a=b$ , այսինքն՝ բոլոր թվերը հավասար են։

Սխալի պատճառ. քանի որ $a-b=c$ , մենք իրավունք չունենք կրճատել $(a-b-c)$ -ով, որովհետև այդ արտահայտությունը հավասար է զրոյի, իսկ 0-ով կրճատել (այսինքն՝ բաժանել զրոյի վրա) չի կարելի^[6]։

Զրոյի վրա բաժանումը հանրահաշվական ամենատարածված սխալներից է, ընդ որում՝ այդ բաժանումը կարող է լինել քողարկված, օրինակ՝ կրճատումն ընդհանուր արտադրիչով։ Օրինակ՝ $9x^{2}=x$ հավասարումը $x$ -ով կրճատելիս մենք կորցնում ենք $x=0$ արմատը։ Մեկ այլ հավասարման սոփեստություն.

{\sqrt {x-5}}\cdot x=4{\sqrt {x-5}}

:

Կրճատելով $({\sqrt {x-5}})$ -ով՝ մենք ոչ միայն կորցնում ենք հավասարման միակ արմատը՝ $x=5$ , այլև միաժամանակ ստանում ենք $x=4$ ավելորդ արմատը, որը չի պատկանում անհայտի թույլատրելի արժեքների բազմությանը, քանի որ արմատատակ արտահայտությունը $x=4$ դեպքում դառնում է բացասական^[7]։

Անհավասարություններ[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ Դիցուք $a$ -ն և $b$ -ն կամայական դրական թվեր են, ընդ որում՝ $a>b$ : Անհավասարության երկու մասերը բազմապատկենք $b$ -ով և երկու մասից հանենք $a^{2}$ , կստանանք՝ $ab-a^{2}>b^{2}-a^{2}$ : Վերլուծենք արտադրիչների՝

a(b-a)>(b+a)(b-a)

Կրճատենք $(b-a)$ -ով (ենթադրելով, որ այն հավասար չէ զրոյի), կստանանք $a>b+a$ անհավասարությունը։ Երկու մասից հանենք $a$ , կստանանք $0>b$ : Այսինքն՝ ցանկացած դրական $b$ թիվ միաժամանակ բացասական է։

Սխալի պատճառ. անհավասարության երկու մասերը կարելի է կրճատել ընդհանուր արտադրիչով, բայց եթե արտադրիչը բացասական է, ապա անհավասարության նշանը փոխվում է հակառակ նշանով։ Այստեղ հենց այդ դեպքն է, քանի որ $b-a<0$ : Կրճատումից հետո ստանում ենք $a<b+a$ , սխալն վերացված է^[8]։

Արմատի հանում[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ $1-3+{\frac {9}{4}}=4-6+{\frac {9}{4}}$ ճիշտ հավասարությունը կարելի է գրել $\left(1-{\frac {3}{2}}\right)^{2}=\left(2-{\frac {3}{2}}\right)^{2}$ տեսքով։ Քառակուսի արմատ հանելով՝ ստանում ենք $1-{\frac {3}{2}}=2-{\frac {3}{2}}$ , որից՝ $1=2$ :

Սխալի պատճառ. մեծությունների արմատների հավասարությունից հետևում է այդ մեծությունների հավասարությունը միայն այն դեպքում, եթե նրանք ունեն նույն նշանը։ արմատի ճիշտ հանումը տալիս է բացարձակ արժեքով արդյունք. $\left|1-{\frac {3}{2}}\right|=\left|2-{\frac {3}{2}}\right|$ , և այդ դեպքում սխալ չի առաջանում^[9]։

Սոփեստություն 2։ Թիվն աստիճան կարելի է բարձրացնել ոչ միայն ամբողջ, այլև կոտորակային ցուցիչով. $a^{m/n}=({\sqrt[{n}]{a}})^{m}$ : Դիտարկենք սոփեստություն, որն ապացուցում է, որ $-1=1$ :

-1=(-1)^{2\ \cdot \ {\frac {1}{2}}}=\left({(-1)^{2}}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}={\color {blue}{\sqrt {\color {black}1}}}=1

Սխալի պատճառ. կոտորակային ցուցիչով աստիճան կարելի է բարձրացնել միայն ոչ բացասական թվերը^[10]։

Սոփեստություն 3։ Պետք է զգուշություն ցուցաբերել եռանկյունաչափական ֆունկցիաները կոտորակային ցուցիչով աստիճան բարձրացնելիս։ Թվում է՝ ակնհայտ է, որ $(\cos ^{2}x)^{3/2}=\cos ^{3}x$ , սակայն $x=\pi$ դեպքում ստանում ենք սխալ հավասարություն՝ $1^{3/2}=-1$ : Քանի որ թվի քառակուսու արմատը հավասար է թվի բացարձակ արժեքին, հետևաբար ճիշտ գրությունը հետևյալն է^[11]՝ $(\cos ^{2}x)^{3/2}=|\cos x|^{3}$ :

Խնդրի սխալ պայմաններ[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ Լուծենք հետևյալ հավասարումը. $3{\sqrt {x}}+x+2=0$ :

3{\sqrt {x}}=-(x+2);\quad 9x=x^{2}+4x+4;\quad x^{2}-5x+4=0

x_{1}=4;\quad x_{2}=1

Ստուգում. առաջին արմատը տեղադրելով հավասարման մեջ՝ կստացվի $12=0$ հավասարությունը, երկրորդ արմատը տեղադրելով՝ $6=0$ հավասարությունը։

Սխալի պատճառ. տրված հավասարումը լուծում չունի։ Դա երևում է այն բանից, ձախ մասը մեծ կամ հավասար է զրոյից $(x\geqslant 0$ , քանի որ այն արմատի տակ է)։ Քառակուսի բարձրացնելիս ի հայտ են գալիս երկու լրացուցիչ արմատներ, բայց ստուգումը դրանք ժխտում է^[12]։

Սոփեստություն 2։ Լուծենք հետևյալ հավասարումը՝ $x^{2}-ax=-{\frac {1}{3}}a^{2}$ , որտեղ $a$ -ն կամայական իրական թիվ է։

Երկու մասերը բազմապատկենք $(-3a)$ -ով, այնուհետև ավելացնենք $x^{3}-a^{3}$ , հավասարումը կստանա $(x-a)^{3}=x^{3}$ տեսքը։ Խորանարդ աստիճանի արմատ հանելով՝ կստացվի $x-a=x$ հավասարումը, այդտեղից էլ՝ $a=0$ , այսինքն՝ բոլոր թվերը հավասար են զրոյի։

Սխալի պատճառ. անհայտ $x$ -ն ընդունում ենք որպես իրական թիվ, սակայն տրված հավասարումը չունի իրական արմատներ (բացառությամբ հենց $a=0$ դեպքը), որովհետև նրա տարբերիչը՝ $D=-a^{2}/3\leqslant 0$ : Իսկ եթե հավասարումը դիտարկենք կոմպլեքս թվերի համակարգում, ապա բոլոր դատողությունները մինչև խորանարդ աստիճանի արմատ հանելը ճիշտ են, բայց կոմպլեքս խորանարդ ասիճանի արմատն ունի երեք արժեք, այդ պատճառով խորանարդ աստիճանի արմատների հավասարությունից չի հետևում, որ այդ մեծությունները նույնպես հավասար են^[13]։

Երկրաչափություն[խմբագրել | խմբագրել կոդը]

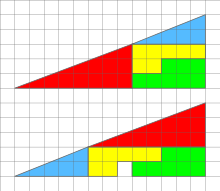
Սոփեստություն 1։ Եռանկյունին կտրում ենք չորս մասի, ինչպես ցույց է տրված նկարի վերևի մասում, իսկ այնուհետև այդ մասերից կառուցում ենք նույն մեծությամբ նոր եռանկյուն, ինչպես ցույց է տրված նկարի ներքի մասում։ Մասերի տեղափոխության արդյունքում ընդհանուր մակերեսը փոխվում է մեկ վանդակով։

Սխալի պատճառ. ուղիղը, որը կարծես եռանկյան ներքնաձիգն է, իրականում բեկյալ է, այսինքն՝ տվյալ պատկերը ոչ թե եռանկյուն է, այլ քառանկյուն։ Դա հեշտ է եզրակացնել այն այն փաստից, որ կարմիր եռանկյան էջերի հարաբերությունը 3:8 է, իսկ կապույտ եռանկյունինը՝ 2:5, ինչ մի փոքր ավելի մեծ է։ Նշանակում է, որ վերևի պատկերում բեկյալը մի փոքր գոգավոր է, ներքևում՝ մի փոքր ուռուցիկ, և մակերեսների տարբերությունն էլ տալիս է հենց «ավելորդ» վանդակը^[14]։

Սոփեստություն 2։ Հիմնվենք հետևյալ հայտանիշի վրա. երկու եռանկյուններ հավասար են, եթե հավասար են նրանց երկու կողմերն ու անկյուններից մեկը։ ABC и ABC' եռանկյուններն ունեն երկու հավասար կողմ ( $b=b'$ ) և անկյուն $\beta$ -ն, նշանակում է, որ դրանք հավասար են, ինչը հակասում է կառուցմանը։

Սխալի պատճառ. եռանկյունների հավասարության անուշադիր, և, հետևաբար, սխալ ձևակերպված հայտանիշի ճիշտ տարբերակն է. «երկու եռանկյուններ հավասար են, եթե հավասար են նրանց երկու կողմերն ու նրանցով կազմած անկյունը»։ Փաստորեն, այս սոփեստությունը կարելի է դիտարկել որպես սխալ հայտանիշի համոզիչ հերքում^[15]։

Սոփեստություն 3. «բոլոր եռանկյունները հավասարասրուն են» (հաճախ վերագրվում է Լուիս Քերոլին^[16])^[17]: Դիտարկենք ABC կամայական եռանկյունը (տե՛ս նկարը)։ Անկյուն A-ի կիսորդը և BC կողմին նրա միջնակետում տարված ուղղահայացը հատվում են ինչ-որ O կետում։ O կետից տանենք OR (AB կողմին) և OQ (AC կողմին) ուղղահայացները, ինչպես նաև O-ն միացնենք B և C գագաթներին։

RAO և QAO ուղղանկյուն եռանկյունները հավասար են, քանի որ ունեն ընդհանուր կողմ (AO) և մեկ հավասար անկյուն (∠RAO=∠QAO): Հավասար են նաև ROB և QOC ուղղանկյուն եռանկյունները, քանի որ հավասար են նրանց երկու կողմերը՝ BO=OC և RO=OQ: Այդ դեպքում՝ AR=AQ, RB=QC, իսկ AB=AR+RB=AQ+QC=AC, այսինքն՝ եռանկյունը հավասարասրուն է։

Սխալի պատճառ. միտումնավոր աղավաղված հայտանիշ։ Եթե այն կատարենք ուշադիր, ապա O-ն կլինի ոչ թե եռանկյան ներսում, այլ՝ դրսում։ Ավելին, R և Q կետերից մեկը գտնվում է եռանկյան կողմի վրա, մյուսը՝ մյուս կողմի շարունակության վրա. եթե $AB>AC$ , ապա R կետը եռանկյան ներսում է, Q-ն՝ դրսում, հակառակ դեպքում հակառակը։ Առաջին դեպքում $AB=AR+RB;AC=AQ-QC$ . գումարածի փոխարեն հանած, համանման ձևով վերլուծվում է երկրորդ դեպքը^[18]։

Եռանկյունաչափություն[խմբագրել | խմբագրել կոդը]

Սոփեստություն։ Դիտարկենք հայտնի եռանկյունաչափական ֆունկցիաները. $\sin(\pi -\alpha )=\sin \alpha$ : Ցանկացած եռանկյան մեջ եռանկյան անկյունների գումարը 180° է կամ $\alpha +\beta +\gamma =\pi$ , այդ պատճառով $\sin(\pi -(\alpha +\beta ))$ մի դեպքում հավասար է $\sin(\alpha +\beta )$ նույնությանը, մյուս կողմից՝ $\sin \gamma$ -ի։ Հետևաբար անկյունները նույնպես հավասար են. $\alpha +\beta =\gamma$ : Այդ հավասարությունը հանելով $\alpha +\beta +\gamma =\pi$ նույնությունից, կստանանք $2\gamma =\pi$ կամ $\gamma =\pi /2$ : Եզրակացություն. ցանկացած եռանկյուն ուղղանկյուն է։

Սխալի պատճառ. $\sin(\alpha +\beta )=\sin \gamma$ հավասարությունը գործում է բոլոր ցանկացած եռանկունու համար, սակայն դրանից չի հետևում անկյունների հավասարությունը. դա ցույց է տալիս նաև $\sin(\pi -\alpha )=\sin \alpha$ բանաձևը։ Ցանկացած երկու անկյուն, որոնք միմյանց լրացնում են մինչև $\pi$ , ունեն նույն սինուսը^[19]։

Ապացույց ինդուկցիայով[խմբագրել | խմբագրել կոդը]

Սոփեստություն։ Ապացուցենք, որ բոլոր ձիերը նույն գույնի են։ Ապացուցումը կատարում ենք ինդուկցիայով $N$ թվով ձիերի համար։ Եթե $N=1$ , պնդումն անշան է։ Ենթադրենք $N$ ձիերից կազմված բոլոր երամակների ձիերը նույն գույնի են, ապացուցենք $N+1$ ձիերից կազմված երամակի համար։ Հանենք մեկ ձին, մնացած բոլոր ձիերը նույն գույնի են ըստ ինդուկցիայի ենթադրության։ Ձին վերադարձնենք երամակ և հեռացնենք մեկ այլ ձի։ Այդ ժամանակ էլ նախորդ անգամ հանված ձին կլինի նույն գույնի։

Սխալի պատճառ. ապացույցի երկրորդ մասը չի գործում $N=2$ դեպքում (ձիուն հեռացնելու հնարքն այդ դեպքում ոչինչ չի ապացուցում)^[20]։

Այս սրամիտ սոփեստությունն ունի մի հետաքրքիր տարատեսակ. ապացույցը պնդում է, որ բոլոր ամբողջ թվերը հավասար են։ Ինդուկցիայի մեթոդով ապացուցենք բնական թվերի $N$ երկարությամբ հատվածի համար՝ $1,2,3,\dots ,N$ : $N=1$ դեպքում հատվածում կա մեկ թիվ, և պնդումը ճշմարիտ է։ Ենթադրենք պնդումը ճիշտ է առաջին $N$ թվերի համար, ապացուցենք $(N+1)$ -ի համար։ Վերցնենք երկու կամայական այնպիսի թիվ, որ $1\leqslant a,b\leqslant N+1$ : Ինդուկցիայի ենթադրության համաձայն՝ $a-1=b-1$ , բայց այդ դեպքում նաև $a=b$ , ինչը և պետք է ապացուցվեր։ Սխալն այստեղ երկրորդի նման է. 2 երկարությամբ հատվածի համար $a=1,b=2$ , $a-1$ նշանակումը դուրս է գալիս ինդուկցիայի ենթադրության սահմաններից՝ խախտելով ապացույցի տրամաբանությունը^[21]։

Բարձրագույն մաթեմատիկա[խմբագրել | խմբագրել կոդը]

Կոմպլեքս թվեր[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ Կեղծ միավորը սահմանվում է որպես ${\sqrt {-1}}$ , այնպես, որ $i^{2}=-1$ : Սակայն $i^{2}={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)\cdot (-1)}}={\sqrt {1}}=1$ : Ստացվում է, որ $1=-1$ :

Սխալի պատճառ. Կոմպլեքս թվերի համակարգում արմատների հետ պետք է զգուշությամբ վարվել։ Արմատը սահմանվում է միայն իրական դրական թվերի համար, իսկ բացասական թվերի կոմպլեքս քառակուսի արմատները երկարժեք են։ Այդ պատճառով ${\sqrt {1}}=1$ հավասարությունը պետք է փոխարինվի ${\sqrt {1}}=\pm 1$ հավասարությունով, և այդ դեպքում սխալ չի առաջանա^[22]։

Սոփեստություն 2։ $e^{2\pi i}=1$ հայտնի նույնությունը բարձրացնենք $i$ աստիճան։ Ձախ մասում կստացվի $e^{-2\pi }$ , աջ մասում՝ հավանաբար 1։ Արդյունքում՝ $e^{-2\pi }=1$ , որը, ինչպես հեշտությամբ կստուգվի, սխալ է։

Սխալի պատճառ. կոմպլեքս աստիճան բարձրացնելը տալիս է բազմարժեք արդյունք, այդ պատճառով $\left(a^{b}\right)^{c}=a^{bc}$ կանոնն այստեղ կիրառելի չէ։ Պետք է օգտագործել ընդհանուր սահմանումը։

Ֆունկցիաների սահմաններ[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ Գտնենք ${\frac {ax+y}{x+ay}}$ արտահայտության սահմանը, երբ $x,y\to \infty$ : Եթե սկզբում դիտարկենք $x\to \infty$ , ապա սահմանը հավասար է $a$ (անկախ $y$ -ի արժեքից), իսկ եթե սկսենք $y$ -ից, ապա սահմանը հավասար է $1/a$ : Ստացվում է, որ յուրաքանչյուր թիվ հավասար է իր հակադարձին։

Սխալի պատճառ. սխալը միայն վերջնական հետևության մեջ է։ Մասնակի սահմանների հերթականության փոփոխությունը կարող է փոխել արդյունքը^[23]։

Գործողություններ անվերջ թվային շարքերի հետ[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ Դիտարկենք թվային շարքը $\ln 2$ բնական լոգարիթմի համար, որն ստացվում է Մերկատորի շարքից $x=1\colon$ դեպքում. $\ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-{\frac {1}{6}}\dots$ Խմբավորենք նույն նշանն ունեցող անդամները.

\ln 2=\left(1+{\frac {1}{3}}+{\frac {1}{5}}\dots \right)-\left({\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}\dots \right)=\left(1+{\frac {1}{3}}+{\frac {1}{5}}\dots \right)+\left({\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}\dots \right)-2\left({\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}\dots \right)

Միավորելով առաջին երկու փակագծերը և 2 արտադրիչը տանելով երրորդ փակագծի մեջ՝ ստանում ենք երկու հավասար մեծությունների տարբերություն, այսինքն՝ զրո, չնայած $\ln 2$ հավասար չէ զրոյի։

\ln 2=\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}\dots \right)-\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}\dots \right)=0

Սխալի պատճառը. թվային շարքի անդամների ոչ բոլոր խմբավորումներն են թույլատրելի. այն ճիշտ է միայն բացարձակ զուգամետ շարքի համար։ Մասնավորապես, տրված զուգամետ թվային շարքի ներկայացումը երկու տարամետ շարքերի տարբերության ձևով ճիշտ չէ։ $1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\dots$ շարքը կոչվում է «հարմոնիկ», և այն տարամիտվում է, չնայած տարբերվում է տրվածից միայն անդամների նշաննեով^[24]։

Ինտեգրալ[խմբագրել | խմբագրել կոդը]

Անորոշ ինտեգրալ[խմբագրել | խմբագրել կոդը]

Սոփեստություն։ Գտնենք հետևյալ երկու նույնությունների ինտեգրալները.

{\frac {d}{dx}}\sin ^{2}x=2\sin x\cos x;\quad {\frac {d}{dx}}\cos ^{2}x=-2\sin x\cos x

:

Արդյունքները.

\int {\sin x\cos xdx}={\frac {1}{2}}\sin ^{2}x;\quad \int {\sin x\cos xdx}=-{\frac {1}{2}}\cos ^{2}x

Առաջին հավասարությունից հանելով երկրորդը՝ կստանանք.

\sin ^{2}x+\cos ^{2}x=0

,

այնինչ աջ մասը պետք է լիներ 1։

Սխալի պատճառ. անորոշ ինտեգրալի նշանակումների մեջ մոռացել ենք ներառել ինտեգրման հաստատունները^[25].

\int {\sin x\cos xdx}={\frac {1}{2}}\sin ^{2}x+C_{1};\quad \int {\sin x\cos xdx}=-{\frac {1}{2}}\cos ^{2}x+C_{2}

Որոշյալ ինտեգրալ[խմբագրել | խմբագրել կոդը]

Սոփեստություն 1։ Նյուտոն-Լեյբնիզ բանաձևով գտնենք դրական ֆունկցիայի ինտեգրալը.

\int \limits _{-1}^{1}{\frac {dx}{x^{2}}}=-{\frac {1}{x}}{\bigg |}_{-1}^{1}=-1-1=-2

:

Դրական ֆունկցիայի ինտեգրալն ստացվեց բացասական («Դալամբերի պարադոքս», 1768 թվական)^[26]։

Սխալի պատճառ. ինտեգրված ֆունկցիան խզվում է 0 կետում (և սահմանափակ չէ), այդ պատճառով Նյուտոն-Լեյբնիզ բանաձևը նրա նկատմամբ կիրառելի չէ։

Սոփեստություն 2։ Դրական ֆունկցիայի ինտեգրալը որոշենք փոփոխականի փոխարինման մեթոդով.

I=\int \limits _{-1}^{1}x^{2}dx

Ներմուծենք նոր փոփոխական՝ $y=x^{2};dy=xdx$ ; $x$ -ի համար ինտեգրման $[-1;1]$ հատվածը $y$ -ի համար տեղափոխվում է $[1;1]$ հատված։

I=\int \limits _{1}^{1}{\sqrt {y}}dy=0

: Ճիշտ պատասխանն է՝

I={\frac {2}{3}}

:

Սխալի պատճառ. փոփոխականը փոխարինելիս հին և նոր փոփոխականները պետք է գտնվեն փոխմիարժեք համապատասխանության մեջ, այլապես $x=x(y)$ հակադարձ ֆունկցիան որոշված չէ^[27], սոփեստության մեջ այդ կանոնը խախտված է։

Այլ սոփեստություններ[խմբագրել | խմբագրել կոդը]

Սխալ դատողության մի քանի լրացուցիչ օրինակներ, որոնք աշխույժ քննարկում են առաջացրել գիտական համայնքում.

Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]

↑ Софизм // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — С. 1241. — 1600 с.
↑ ^2,0 ^2,1 ^2,2 Мадера А. Г., Мадера Д. А., 2003, էջ 3—4
↑ ^3,0 ^3,1 Брадис и др., 1959, էջ 7—11
↑ Обреимов, 1889
↑ ^5,0 ^5,1 Брадис и др., 1959, էջ 11—14
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 9
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 65—66
↑ Брадис и др., 1959, էջ 89—90
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 6
↑ Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М.: Мнемозина, 2003. — С. 253—255. — 376 с.
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 16
↑ Брадис и др., 1959, էջ 58
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 7—8, 66—67
↑ «Curry Triangle Paradox». Վերցված է 2019 թ․ օգոստոսի 31-ին.
↑ Երկու կողմերով և նրանցով կազմած անկյան միջոցով եռանկյուն կառուցելու խնդրի վերլուծությունը տես Եռանկյունների լուծում հոդվածում կամ հետևյալ ուղեցույցում. Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978. — С. 294.
↑ Իրականում սոփեստությունն առաջին անգամ հրատարակվել է հետևյալ գրքում՝ Ball W. W. R. Mathematical Recreations and Essays (1892 год), որտեղից էլ այն վերցրել է Քերոլը։
↑ Robin Wilson (2008), Lewis Carroll in Numberland, Penguin Books, էջեր 169–170, ISBN 978-0-14-101610-8
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 21—23, 81—82
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 45—46, 66—67
↑ Пойа, Д. Математика и правдоподобные рассуждения. — Изд. 2-е, исправленное. — М.: Наука, 1975. — С. 140.
↑ Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — С. 274. — 216 с. — ISBN 978-5-397-02435-8
↑ Брадис и др., 1959, էջ 81—82
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 17, 76
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 15, 73—75
↑ Мадера А. Г., Мадера Д. А., 2003, էջ 39, 94
↑ Марков С. Н. Курс истории математики: Учебное пособие. — Иркутск: Издательство Иркутского университета, 1995. — С. 167. — 248 с. — ISBN 5-7430-0496-X
↑ Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. — М.: Высшая школа, 1972. — 640 с.

Գրականություն[խմբագրել | խմբագրել կոդը]

Брадис В. М. Минковский В. Л., Харчева А. К. Ошибки в математических рассуждениях. — 2-е изд. — М.: Учпедгиз, 1959. — 177 с.
- 3-е издание: М.: Просвещение, 1967. — 191 с.
Гарднер, Мартин Геометрические заблуждения (глава 6) // Крестики-нолики. — М.: Мир, 1988. — 325 с. — ISBN 5-03-001234-6
Гарднер, Мартин Математические софизмы (глава 13) // Математические головоломки и развлечения. — М.: Мир, 1971. — 511 с.
Мадера А. Г., Мадера Д. А. Математические софизмы. Правдоподобные рассуждения, приводящие к ошибочным утверждениям. / Книга для учащихся 7—11 классов. — М.: Просвещение, 2003. — 112 с. — ISBN 5-09-010795-5
Обреимов В. И. Математические софизмы. — 2-е изд. — Спб.: Ф. Павленков, 1889. — 79 с.
Перельман Я. И. Дважды два — пять! (Математические софизмы).. — Л.: ДЗН, 1839. — 16 с.
Фурре, Эмиль. Геометрическiе головоломки и паралогизмы. — Одесса: Mathesis, 1912. — 52 с.

Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]

«Մաթեմատիկական սոփեստություններ». Mathemlib — մաթեմատիկական գրադարան. Վերցված է 2019 թ․ օգոստոսի 27-ին.

[1] Софизм // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — С. 1241. — 1600 с.

[MM3-2] 2,0 ^2,1 ^2,2 Мадера А. Г., Мадера Д. А., 2003, էջ 3—4

[Брадис_и_др.—1959——7—11-3] 3,0 ^3,1 Брадис и др., 1959, էջ 7—11

[Обреимов—1889——-4] Обреимов, 1889

[BRA11-5] 5,0 ^5,1 Брадис и др., 1959, էջ 11—14

[Мадера_А._Г.,_Мадера_Д._А.—2003——9-6] Мадера А. Г., Мадера Д. А., 2003, էջ 9

[Мадера_А._Г.,_Мадера_Д._А.—2003——65—66-7] Мадера А. Г., Мадера Д. А., 2003, էջ 65—66

[Брадис_и_др.—1959——89—90-8] Брадис и др., 1959, էջ 89—90

[Мадера_А._Г.,_Мадера_Д._А.—2003——6-9] Мадера А. Г., Мадера Д. А., 2003, էջ 6

[10] Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М.: Мнемозина, 2003. — С. 253—255. — 376 с.

[Мадера_А._Г.,_Мадера_Д._А.—2003——16-11] Мадера А. Г., Мадера Д. А., 2003, էջ 16

[Брадис_и_др.—1959——58-12] Брадис и др., 1959, էջ 58

[Мадера_А._Г.,_Мадера_Д._А.—2003——7—8,_66—67-13] Мадера А. Г., Мадера Д. А., 2003, էջ 7—8, 66—67

[14] «Curry Triangle Paradox». Վերցված է 2019 թ․ օգոստոսի 31-ին.

[15] Երկու կողմերով և նրանցով կազմած անկյան միջոցով եռանկյուն կառուցելու խնդրի վերլուծությունը տես Եռանկյունների լուծում հոդվածում կամ հետևյալ ուղեցույցում. Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978. — С. 294.

[16] Իրականում սոփեստությունն առաջին անգամ հրատարակվել է հետևյալ գրքում՝ Ball W. W. R. Mathematical Recreations and Essays (1892 год), որտեղից էլ այն վերցրել է Քերոլը։

[17] Robin Wilson (2008), Lewis Carroll in Numberland, Penguin Books, էջեր 169–170, ISBN 978-0-14-101610-8

[Мадера_А._Г.,_Мадера_Д._А.—2003——21—23,_81—82-18] Мадера А. Г., Мадера Д. А., 2003, էջ 21—23, 81—82

[Мадера_А._Г.,_Мадера_Д._А.—2003——45—46,_66—67-19] Мадера А. Г., Мадера Д. А., 2003, էջ 45—46, 66—67

[20] Пойа, Д. Математика и правдоподобные рассуждения. — Изд. 2-е, исправленное. — М.: Наука, 1975. — С. 140.

[21] Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — С. 274. — 216 с. — ISBN 978-5-397-02435-8

[Брадис_и_др.—1959——81—82-22] Брадис и др., 1959, էջ 81—82

[Мадера_А._Г.,_Мадера_Д._А.—2003——17,_76-23] Мадера А. Г., Мадера Д. А., 2003, էջ 17, 76

[Мадера_А._Г.,_Мадера_Д._А.—2003——15,_73—75-24] Мадера А. Г., Мадера Д. А., 2003, էջ 15, 73—75

[Мадера_А._Г.,_Мадера_Д._А.—2003——39,_94-25] Мадера А. Г., Мадера Д. А., 2003, էջ 39, 94

[26] Марков С. Н. Курс истории математики: Учебное пособие. — Иркутск: Издательство Иркутского университета, 1995. — С. 167. — 248 с. — ISBN 5-7430-0496-X

[27] Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. — М.: Высшая школа, 1972. — 640 с.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]