Մաթեմատիկայի պատմություն

Մաթեմատիկայի պատմության մեջ ավանդաբար առանձնացվում են մաթեմատիկական գիտելիքների զարգացման մի քանի փուլեր.
- Երկրաչափական պատկերների և թվերի՝ որպես իրական օբյեկտների ու բազմությունների միատարր օբյեկտի հասկացության ձևավորում։ Ձևավորվեցին չափ և հաշիվ հասկացությունները, որոնք թույլ տվեցին համեմատել տարբեր թվեր, երկարություններ, մակերեսներ և ծավալներ։
- Հանրահաշվական գործողությունների հայտնաբերում։ Հանրահաշվական գործողությունների հատկությունների, պարզ պատկերների և մարմինների մակերեսների և ծավալների հաշվման եղանակների մասին գիտելիքների կուտակում էմպիրիկ եղանակով (դիտարկման մեթոդով)։ Այս ուղղությամբ ավելի մեծ տեղեկատվություն էր տրվում շումեր–բաբելոնյան, չինացի և հնդիկ մաթեմատիկոսները։
- Հին Հունաստանում մաթեմատիկական դեդուկցիայի մեթոդի ձևավորում, որը ցույց տվեց, թե ինչպես ստանալ նոր մաթեմատիկական ճշմարտություններ, արդեն գոյություն ունեցող ճշմարտությունների հիման վրա։ Հին հունական մաթեմատիկայի գլխավոր ձեռքբերումը Էվկլիդեսի «Սկզբունքներ» աշխատությունն էր։
- Իսլամի մաթեմատիկոսները ոչ միայն պահպանեցին անտիկ ձեռքբերումները, այլև իրականացրեցին դրանց սինթեզը հնդիկ մաթեմատիկոսների բացահայտումների հետ, որոնք բավական մեծ առաջընթաց ունեին թվերի տեսության ոլորտում։
- 16-18-րդ դարեում ծնվում և բավական մեծ առաջընթաց է ապրում եվրոպական մաթեմատիկական գիտությունը։ Այս փուլում նրա կոնցեպտուալ հիմքը համարվում էր այն, որ մաթեմատիկական մոդելները հանդիսանում են Տիեզերքի յուրահատուկ կմախք[2], այդ պատճառով մաթեմատիկական մոդելների նոր հատկությունների ձևավորումը հնարավորություն է տալիս բացահայտել իրական աշխարհի նորանոր հատկություններ։ Ձևավորվեց ֆունկցիայի գաղափարը։ Բոլոր բնական գիտությունները սկսեցին վերակառուցվել նոր հայտնաբերված մաթեմատիկական մոդելների հիմնքի վրա, որը բերեց նրանց արագ զարգացմանը[3]։
- 19-20-րդ դդ. պարզ դարձավ, որ մաթեմատիկայի և իրական աշխարհի փոխհարաբերությունները այքան էլ պարզ չէին, ինչպես թվում էր։ Ձևավորվեցին մաթեմատիկական մի շարք ուղղություններ[4]։
Մաթեմատիկայի էվոլյուցիայի վերլուծությունը, բացի պատմական մեծ հետաքրքրություն ներկայացնելուց, մեծ նշանակություն ունի մաթեմատիկայի մեթոդաբանության և փիլիսոփայության զարգացման գործում։ Մաթեմատիկական պատմության իմացությունը շատ հաճախ նպաստում է մաթեմատիկայի կոնկրետ ճյուղերի զարգացմանը, օրինակ՝ հին չինական մնացորդների մասին թեորեմի կամ վարժության հիման վրա ձևավորվեց մի ամբողջական բաժին՝ թվերի տեսությունը։
Հանրահաշվի և երկրաչափության ծագումը[խմբագրել | խմբագրել կոդը]
Մաթեմատիկան մարդկային գիտությունների համակարգում մի բաժին է, որն զբաղվում է այնպիսի հասկացությունների ուսումնասիրությամբ, ինչպիսիսք են կառուցվածքը, քանակը, հարաբերությունը և այլն։ Մաթեմատիկայի զարգացումը սկսվեց գծերի, մակերևույթների հաշվման ու չափման արվեստների գործնական ձևավորմամբ։
Բնական թվերի մասին գաղափարը ձևավորվել է աստիճանաբար և բարդացել նախնադարյան մարդու՝ թվային աբստրակցիան նրա կոնկրետ պատկերացումներից տարբերել չկարողանալու պատճառով։ Դրա հետևանքով հաշիվը երկար ժամանակ մնում էր միայն տեսական հիմքի վրա՝ հաշվելու համար օգտագործվում էին իրենց մատները, քարերը և այլն։
Մեծ քանակություններով հաշվման տարածմամբ ձևավորվեց միտք՝ հաշվել ոչ միայն միավորներով, այլև այսպես ասած միավորների փաթեթներով՝ օրինակ 10 օբյեկտով։ Այդ գաղափարը միանգամից արտացոլվեց լեզվի մեջ, իսկ հետո գրավոր ձևով։ Հաշվման արդյունքն հիշելու համար օգտագործում էին թելիկներ և այլ իրեր։ Գրելու արվեստի զարգացման հետ մեկտեղ սկսեցին օգտագործել նաև տառեր կամ հատուկ նշաններ՝ մեծ թվերի կրճատ պատկերման համար։
Երկուսից մինչև տասը թվերի անվանումները և 100 թվի անվանումը հնդեվրոպական լեզուներում նման են։ Դա ասում է այն մասին, որ վերացական թվի գաղափարը ձևավորվել է շատ վաղուց, մինչև այդ լեզուների առանձնացումը։ Հաշվիչ գործիքների ստեղծմանը զուգընթաց ժողովուրդների մեծ մասի մոտ 10 թիվը կարևոր տեղ է գրավում, ուստի պարզ է, որ մատների վրա հաշվելը լայն կիրառություն է ունեցել։
Այստեղից է տարածվել բոլորին հայտնի տասը հիմնային համակարգի գաղափարը։ Երբ վերացական թվի գաղափարը վերջնականապես հաստատվեց, հաջորդ քայլը դարձավ գործողություննայդ թվերի հետ։
Բնական թիվը՝ դա միատարր՝ կայուն և անբաժանելի առարկաների վերջավոր բազմության իդեալիզացիան է։ Հաշվի համար անհրաժեշտ է ունենալ այնպիսի կարևոր իրադարձությունների մաթեմատիկական մոդելներ, ինչպիսիք են մի քանի բազմությունների միավորումը կամ մի բազմության առանձնացումը մի քանի բազմությունների։ Այդպես ձևավորվեցին գումարման և հանման գործողությունները։
Բնական թվերի բազմապատկումը ձևավորվեց որպեսփաթեթային բազմապատկում։ Գործողությունների հատկաությունները և դևանց կապը բացահայտվում էր աստիճանաբար։
Մյուս կարևոր գործողություն է հանդիսանում բաժանումը մի քանի մասի, ժամանակի ընթացքում այն վերածվեց 4-րդ հանրահաշվական գործողության-բաժանում։ Բաժանել 10 մասի դժվար է, այդ պատճառով տասնորդական կոտորակները, որոնք հարմար են բարդ հաշվումների ժամանակ, հանդես եկան համեմատաբար ավելի ուշ։ Առաջին կոտորակները հիմնականում որպես հայտարար ունեին 2, 3, 4, 8, 12 թվերը։ Օրինակ հռոմեացիների մոտ ստանդարտ կոտորակ էր համարվում ունցիան 1/12 -ը։
Մոտավորապես նույն ժամանակահատվածում, ինչպես, որ տառերը, մարդը վերացարկում էր հարթաչափական և տարածաչափական մարմիններ։ Նրանք հիմնականում կրում էին իրենց նման իրական պատկերների անվանումները։ Օրինակ՝ հին հույների մոտ «ռոմբոս»-ը նշանակում է սեղան, «սֆերա»-ն գնդակ։
Չափման տեսությունը ձևավորվել է բավական ուշ և պարունակում էր շատ սխալներ՝ բնութագրիչ օրինակ է պատկերների մակերեսների հավասարությունից պարագծերի հավասարության գաղափարը և հակառակը։ Դա զարմանալի չէ, որպես չափման միավոր վերցված է չափիչ թելը, ուստի պարագծի հաշվումը բավական պարզ գործընթաց էր, իսկ մակերեսի հաշվման համար հարմար սարքեր չկային։ Չափումները ծառայում էին որպես կարևորագույն կոտորակային թվերի և դրանց տեսության զարգացման աղբյուր։
Հին Արևելք[խմբագրել | խմբագրել կոդը]
Մաթեմատիկան Հին Եգիպտոսում[խմբագրել | խմբագրել կոդը]
Հին եգիպտական մաթեմատիկական տեքստերը վերաբերվում են մ.թ.ա. 2-րդ հազարամյակի սկզբին։ Մաթեմատիկան այն ժամանակ օգտագործվում են աստղագիտության մեջ ծովագնացության, երկրաբանության տների շինարարության, ռազմական կառույցների ամրացման մեջ։ Դրամական հաշվարկներ, ինչպես նաև հենց դրամներ Եգիպտոսում չկար։ Եգիպտացիները գրում էին պապիրուսի վրա, որը շատ ցածր որակ ուներ, այդ պատճառով Եգիպտոսի մաթեմատիկայի մասին բավականաչափ քիչ տեղեկություն կա, քան Հունաստանի և Բաբելոնի մաթեմատիկայի մասին։ Հավանաբար, այն ավելի լավ էր զարգացած, քան կարելի է պատկերացնել։
Պահպանված հիմնական աղբյուրները՝ Ախմեսի պապիրուսն է, որը պարունակում էր 84 մաթեմատիկական խնդիր, և Գոլինշևայի մոսկովյան պապիրուսը՝ 25 խնդիր։
Ախմեսի պապիրուսի բոլոր վարժությունները ունեն կիրառական նշանակությունև կապված են շինարարության հետ։ Խնդիրները խմբավորված են ոչ թե ըստ մեթոդի, այլ ըստ թեմայի։ Դրանք վարժություններ են, որոնք վերաբերվում են եռանկյան, քառանկյան, շրջանագծի մակերեսների հաշվումը, ամբողջ թվերի հետ բազմաթիվ գործողությունների իրականացման, մեկ փոփոխական պարունակող առաջին և երկրորդ աստիճանի հավասարումների լուծման հետ։
Ընդհանրապես բացակայում են բոլոր տեսակի ապացույցները կամ բացատրությունները։ Փնտրվող արդյունքը կամ միանգամից է ներկայացվում, կամ բերվում է դրա բացահայտման կարճ ալգորիթմ։ Այսպիսի շարադրումը առկա է հին արևելքի բոլոր երկրների գիտության մեջ, և կարելի է գալ այն համոզման, որ, այն ժամանակներում օգտագործվել է ինդուկտիվ դատողությունների և մտահանգման մեթոդը, որը ոչ մի ընդհանուր տեսություն չի առաջադրում։
Այնուամենայնիվ, պապիրուսում կա վկայությունների մի ամբողջ շարք այն մասին, որ Հին Եգիպտոսում մաթեմատիկան այն ժամանակներում ունի կամ ունեցել է տեսական բնութագիր։ Եգպտացի մաթեմատիկոսները կարողացել են թիվը աստիճան բարձրացնել, թվից արմատ հանել, լուծել հավասարումներ, ծանոթ էին թվաբանական և երկրաչափական պրոգրեսիաներին։ Եգիպտոսում հայտնի են եղել եռանկյան, քառանկյան, սեղանի մակերեսները։
Մաթեմատիկան Հին Չիաստանում[խմբագրել | խմբագրել կոդը]
Թվերը Հին Չինաստանում գրվում էին հատուկ հիերոգլիֆներով, որոնք հայտնվել էին մ.թ.ա. 2-րդ հազարամյակում և նրանց վերջնական տեսքը կազմվել է մ.թ.ա. 3-րդ հազարամյակում։ Այս հիերոգլիֆներն օգտագործվում են նաև ներկայում։ Թվերի գրառման եղանակը Չինաստանում հիրավի ունեցել է մուլտիպլիկատիվ բնույթ։ Օրինակ 1946 թվի գրառումը, հիերոգլիֆների փոխարեն օգտագործելով հռոմեական թվերը կարելի է ներկայացնել 1М9С4Х6։ Սակայն գործնականում, հաշվարկները կատարվում էին հաշվիչ գրատախտակի վրա, որտեղ թվերի գրառումն ուներ այլ ձև։ Գումարումն իրականացվում էր հատուկ հաշվիչ գրատախտակի վրա суаньпань։ Զրոն սկզբում նշանակում էր դատարկ տեղ, հատուկ հիերոգլիֆը հայտնվել է մ.թ. 12-րդ դարում։ Բազմապատկման աղյուսակն հիշելու համար գույություն ուներ հատուկ երգ, որը աշակերտները պետք է սովորեին անգիր։
Հին Չինաստանի մաթեմատիկայի զարգացման ավեիլ ցայտուն օրինակ է «Մաթեմատիկան 9 գրքերում»։ Չինացիներին շատ բան էր հայտնի, այդ թվում՝ հանրահաշվի ամբողջ հիմքը, կոտորակների հետ գործողությունները, բացասական թվերը, հիմնական պատկերների մակերեսները և ծավալները, Պյութագորասի թեորեմը և պյութագորյան եռյակների ընտրության ալգորիթմը, քառակուսային հավասարումների լուծման եղանակները։ Մշակվել էր մեթոդ կամայական թվով հավասարումների համակարգի լուծման համար, որը Գաուսի մեթոդի տիպիկ օրինակն է։
Մաթեմատիկան Հին Հունաստանում[խմբագրել | խմբագրել կոդը]


Մաթեմատիկան այդ բառի ժամանակակից ընկալմամբ ձևավորվել է Հունաստանում։ Էլադայի ժամանակներում գոյություն ունեցող երկրներում մաթեմատիկան օգտագործվում է չափման, հաշվումների համար, կամ կախարդական արարողությունների իրականացման համար։ Մաթեմատիկական տեսություն գոյություն չի ունեցել։
Հույները հետևյալ կերպ են մտածել.
- Պյութագորյան դպրոցը առաջ քաշեց թեզիս «Թվերը տիրում են աշխարհին»։ Կամ ինչպես ձևակերպել են նույն այդ միտքը 2 հազար տարի հետո «Բնությունը խոսում է մեզ հետ մաթեմատիկայի լեզվով». Գալիլեյ։ Դա նշանակում էր, որ մաթեմատիկական ճշմարտությունները իրականում կապված են իրական աշխարհի գոյության հետ։
- Այդպիսի ճշմարտությունների բացահայտման համար պյութագորյան դպրոցի ներկայացուցիչները մշակեցին ավարտուն մեթոդաբանություն։ Սկզբում նրանք կազմել են պարզ, հայտնի մաթեմատիկական ճշմարտություններ՝ աքսիոմներ, պոստուլատներ։ Ապա տրամաբանական դատողությունների հիման վրա այդ ճշմարտություններից դուս են բերվում նոր պնդումներ, որոնք նույնպես պետք է լինեին ճշմարիտ։ Այսպես հայտնվեց դեդուկտիվ մաթեմատիկան։
Հույն մաթեմատիկոսների 2 ձեռքբերում ունեցել են հատկապես մեծ նշանակություն.
- Նրանք կառուցեցին մաթեմատիկան որպես ամբողջական գիտություն, սեփական մեթոդաբանությամբ, որոնք հիմնված են հստակ տրամաբանական օրենքների վրա։
- Նրանք բարձրաձայնեցին, որ բնության օրենքները հասանելի են մարդկային մտածողությանը, և մաթեմատիկական մոդելները այդ երևույթների հասկանալու հիմնական միջոցներ են։ Այս երկու հարաբերություններով հին հունական մաթեմատիկան բավական մոտ է ժամանակակից մաթեմատիկային։
Հնդկաստան[խմբագրել | խմբագրել կոդը]

ՀՀնդկական համարակալումը (թվեր գրելու եղանակ) ի սկզբանե հիասքանչ էր։ Սանսկրիտը թվերն անվանելու միջոցներ ուներ մինչև ։ Թվերի համար առաջին անգամ կիրառվել է սիրո-փյունիկյան համակարգը, իսկ մ․թ․ա․ VI դարից սկսած «բրահմի» ուղղագրությամբ՝՝ 1-9 թվերի համար առանձին նշաններով։ Որոշ փոփոխություններ կրեելով՝ այս նշանները դարձել են ժամանակակից թվեր, որոնք մենք անվանում ենք արաբական, իսկ իրենք՝ արաբները՝ հնդկական։

Մ․ թ․ 500 թվականներին մեզ ամհայտ հնդիկ հանճարեղ մաթեմատիկոս հորինել է թվերի գրության նոր համակարգ՝ տասնորդական դիրքային համակարգը։ Պարզվեց որ թվաբանական գործողություններն այստեղ կատարելը անչափ ավելի հեշտ է, քան հնում՝ ոչ ճկուն տառային ծածկագրերով, ինչպես հույները, կամ սեքսեսիմալ, ինչպես բաբելոնացիները։ Հետագայում հնդիկները օգտագործեցին դիրքային գրառման համար հարմարեցված հաշվման տախտակներ։ Բոլոր թվաբանական գործողությունների համար նրանք մշակեցին ամբողջական ալգորիթմներ , ներառյալ քառակուսի և խորանարդ արմատներ դուրս բերելը։
Հնդիկ ականավոր մաթեմատիկոս և աստղագետ Արյաբհաթայի աշխատանքները թվագրվում են 5-6-րդ դարերով։ Նրա «Արյաբհաթիամ» աշխատության մեջ կան հաշվողական խնդիրների բազմաթիվ լուծումներ։ Մեկ այլ հայտնի հնդիկ մաթեմատիկոս և աստղագետ՝ Բրահմագուպտան, աշխատել է 7-րդ դարում։ Բրահմագուպտայից սկսած հնդիկ մաթեմատիկոսներն ազատ առնչվում են բացասական թվերի հետ՝ դրանք դիտարկելով որպես պարտք։
Միջնադարյան հնդիկ մաթեմատիկոսները մեծագույն հաջողությունների են հասել թվերի տեսության և թվային մեթոդների բնագավառում։ Հնդիկները շատ են առաջադիմել հանրահաշվում. նրանց սիմվոլիկան Դիոֆանտոսի սիմվոլիկայից ավելի հարուստ է, թեև ինչ-որ չափով ծանրաբեռնված է (բառերով ծանրաբեռնված)։ Երկրաչափությունը հնդիկներին ավելի քիչ է հետաքրքրել։Թեորեմների ապացույցները բաղկացած էին գծագրից և «նայեք» բառից։ Նրանք, ամենայն հավանականությամբ, հույներից ժառանգել են մակերեսների և ծավալների, ինչպես նաև եռանկյունաչափության բանաձևերը։
Իսլամական երկրներ[խմբագրել | խմբագրել կոդը]

Արեւելքի մաթեմատիկան, ի տարբերություն հունականի, միշտ էլ ավելի գործնական բնույթ է կրել։Համապատասխանաբար,ավելի մեծ ն7անակություն ունեին հաշվողական և չափման ասպեկտները։ Մաթեմատիկայի կիրառման հիմնական ոլորտներն էին առևտուրը, շինարարությունը, աշխարհագրությունը, աստղագիտությունը և աստղագուշակությունը, մեխանիկան, օպտիկան։
9-րդ դարում ապրել է ալ-Խորեզմին, զրադաշտական քահանայի որդին։ Ուսումնասիրելով հնդկական և հունական գիտելիքները, ալ-Խորեզմին գրել է «Հնդկական հաշվի մասին» գիրքը, այն նպաստել է դիրքային համակարգի հանրայնացմանը ողջ խալիֆայությունում, ընդհուպ մինչև Իսպանիա։ XII դարում այս գիրքը թարգմանվել է լատիներեն, որի հեղինակից է գալիս է «ալգորիթմ» բառը (առաջին անգամ մոտ իմաստով օգտագործել է Լայբնիցը)։ Ալ-Խվարեզմիի մեկ այլ աշխատություն՝ «Համառոտ գիրք Ալ-Ջաբրի և Ալ-Մուկաբալայի հաշվարկի մասին», մեծ ազդեցություն է թողել եվրոպական գիտության վրա և ստեղծել է մեկ այլ ժամանակակից տերմին՝ «հանրահաշիվ»։
Իսլամ մաթեմատիկոսները մեծ ուշադրություն են դարձրել ոչ միայն հանրահաշվին, այլև երկրաչափությանը և եռանկյունաչափությանը (հիմնականում աստղագիտական կիրառությունների համար)։ Նասիր ադ-Դին աթ-Տուսին (13-րդ դար) և Ալ-Քաշին (15-րդ դար) այս ոլորտներում ակնառու աշխատություններ են տպագրել։
Ընդհանուր առմամբ, կարելի է ասել, որ իսլամի երկրների մաթեմատիկոսներին մի շարք դեպքերում հաջողվել է հնդկական կիսաէմպիրիկ մշակումները բարձրացնել տեսական մակարդակի և դրանով իսկ ընդլայնել դրանց հզորությունը։ Թեեւ գործը շատ դեպքերում սահմանափակվում էր այս այդքանով։ Շատ մաթեմատիկոսներ դասական մեթոդների վարպետ էին, սակայն նոր արդյունքներ քիչ ստացվեցին։
Ռուսաստան[խմբագրել | խմբագրել կոդը]
1136 թվականին Նովգորոդի վանական Կիրիկը գրել է մաթեմատիկական ժ աստղագիտական աշխատություն՝ աշխարհի ստեղծման ամսաթվի մանրամասն հաշվարկով[5]։ Ի հավելումն ժամանակագրական հաշվարկների, Կիրիկը բերեց երկրաչափական պրոգրեսիայի օրինակ, որն առաջանում է օրը ավելի փոքր կոտորակների բաժանելուց. Կիրիկը կանգ առավ մեկ միլիոնի վրա՝ հայտարարելով, որ «այլևս չի լինում»։
1701 թվականին կայսերական հրամանագրով Սուխարևյան աշտարակում ստեղծվեց «մաթեմատիկական և նավիգացիոն դպրոց», որտեղ դասավանդում էր Մագնիթսկին։ Պետրոս I-ի հանձնարարությամբ նա գրեց (եկեղեցական սլավոներեն) թվաբանության հայտնի դասագիրք (1703), իսկ ավելի ուշ հրապարակեց նավիգացիոն և լոգարիթմական աղյուսակներ։ Մագնիտսկու դասագիրքը այն ժամանակվա համար բացառիկ հիմնավոր և բովանդակալից էր։ Նա Հեղինակը խնամքով ընտրել էր այն ժամանակ եղած դասագրքերում եղած ամենալավը, նյութը ներկայացրել էր պարզ՝ բազմաթիվ օրինակներով ու բացատրություններով։
Ռուսական գիտության զարգացման հզոր խթան հանդիսացան Միխայիլ Սպերանսկու ձեռնարկած բարեփոխումները։ 19-րդ դարի սկզբին ստեղծվեց Ռուսական կայսրության հանրային կրթության նախարարություն, կազմավորվեցին ուսումնական կենտրոններ, բոլոր խոշոր քաղաքներում բացվեցին գիմնազիաներ։ Ընդ որում մաթեմատիկայի դասընթացի բովանդակությունը բավականին ծավալուն էր՝ հանրահաշիվ, եռանկյունաչափություն, ֆիզիկայի կիրառումներ և այլն։
19-րդ դարում արդեն ռուսական երիտասարդ մաթեմատիկան տվել է համաշխարային մասշտաբի գիտնականներ։
Առաջինը Միխայիլ Վասիլևիչ Օստրոգրադսկին էր։ Ինչպես իրենից առաջ ռուս մաթեմատիկոսներից շատերը, նա առավելապես մշակել է մաթանալիզի կիրառական խնդիրներ։ Նրա աշխատանքներում ուսումնասիրվում է ջերմության տարածումը, ալիքային հավասարումը, առաձգականության տեսությունը և էլեկտրամագնիսականությունը։ Նա նաև ուսումնասիրել է թվերի տեսությունը։ Կարևոր կիրառական աշխատանք է կատարել համաշխարհային հինգ ակադեմիաների ակադեմիկոս Վիկտոր Յակովլևիչ Բունյակովսկին, ով չափազանց բազմակողմանի մաթեմատիկոս էր, գյուտարար, թվերի տեսության և հավանականությունների տեսության ճանաչված հեղինակություն, «Հավանականության մաթեմատիկական տեսության հիմունքներ» հիմնարար աշխատության հեղինակ։

19-րդ դարի առաջին կեսին Ռուսաստանում մաթեմատիկայի հիմնարար հարցերով զբաղվել է միայն Նիկոլայ Իվանովիչ Լոբաչևսկու կողմից, ով դեմ դուրս եկավ Էվկլիդյան տարածության դոգմային։ Նա կառուցեց Լոբաչևսկու երկրաչափությունը և խորապես ուսումնասիրեց դրա անսովոր հատկությունները։ Լոբաչևսկին այնքան առաջ էր իր ժամանակից, որ նա ըստ արժանիքների գնահատվեց մահից շատ տարիներ անց։
Ընդհանուր բնույթի մի քանի կարևոր հայտնագործություններ են արվել Սոֆյա Կովալևսկայայի կողմից։ Նա աշխարհում և պատմության մեջ առաջին կինն էր, ով դարձավ մաթեմատիկայի պրոֆեսոր։ 1874 թվականին Գյոթինգենի համալսարանում պաշտպանել է «Դիֆերենցիալ հավասարումների տեսության մասին» թեզը և ստացել փիլիսոփայության դոկտորի կոչում։ 1889 թվականին Սոֆյա Կովալևսկայան մեծ մրցանակ ստացավ Փարիզի ակադեմիայից՝ ծանր ասիմետրիկ հոլի պտտման վերաբերյալ իր հետազոտության համար[6]։
19-րդ դարի երկրորդ կեսին ռուսական մաթեմատիկան հրապարակեց բավականին հիմնարար արդյունքներ։ Պաֆնուտի Չեբիշև բազմաթիվ հայտնագործություններ է արել մաթեմատիկայի տարբեր ոլորտներում՝ թվերի տեսություն, հավանականությունների տեսություն, ֆունկցիաների մոտարկման տեսություն։.Անդրեյ Մարկովը հայտնի է հավանականությունների տեսության իր առաջին կարգի աշխատանքով, բայց նա նաև ակնառու արդյունքներ է ստացել այլ ոլորտներում՝ թվերի տեսություն և մաթեմատիկական անալիզ։ 19-րդ դարի վերջում ձևավորվեցին երկու ակտիվ հայրենական մաթեմատիկական դպրոցներ՝ Մոսկվան և Սանկտ Պետերբուրգը։
Արևելյան Եվրոպա[խմբագրել | խմբագրել կոդը]
Միջնադար, IV—XV դարեր[խմբագրել | խմբագրել կոդը]

5-րդ դարում եկավ Արևմտյան Հռոմեական կայսրության վերջը, և Արևմտյան Եվրոպայի տարածքը երկար ժամանակ վերածվեց անդադար մարտերի դաշտի ՝ նվաճողների և ավազակների (հուներ, գոթեր, հունգարներ, արաբներ, նորմաններ և այլն) հետ։ Գիտության զարգացումը կանգ էր առել. Մաթեմատիկայի անհրաժեշտությունը սահմանափակվում էր թվաբանությամբ և եկեղեցական տոների օրացույցի հաշվարկով, իսկ թվաբանությունը ուսումնասիրվում էր ըստ Նիկոմաղոս Գերազացու հին դասագրքի՝ Բոետիուսի լատիներեն կրճատ թարգմանությամբ։
Մի քանի բարձր կրթված մարդկանցից կարելի է առանձնացնել իռլանդացի Բեդա Պատվելիին (նա աշխատել է օրացույցի, Զատիկի, ժամանակագրության, մատների վրա հաշվելու տեսության վրա) և վանական Հերբերտին, 999 թվականից՝ Սիլվեստր II պապին՝ գիտությունների հովանավոր; նրան է վերագրվում աստղագիտության և մաթեմատիկայի վերաբերյալ մի քանի աշխատությունների հեղինակ։ Ժամանցային մաթեմատիկական խնդիրների հանրաճանաչ ժողովածուն հրատարակվել է անգլո-սաքսոն բանաստեղծ և գիտնական Ալքուինի կողմից
Եվրոպական մշակույթի կայունացումն ու վերականգնումը սկսվել է 11-րդ դարում։ Հիմնադրվում են առաջին համալսարանները (Սալեռնո, Բոլոնիա)։ Մաթեմատիկայի դասավանդումը ընդլայնվում է. ավանդական քառյակը ներառում էր թվաբանություն, երկրաչափություն, աստղագիտություն և երաժշտություն։

Եվրոպացի գիտնականների առաջին ծանոթությունը հնագույն հայտնագործությունների հետ տեղի է ունեցել Իսպանիայում։ XII դարում այնտեղ թարգմանվել են հանճարեղ հույների և նրանց իսլամ ուսանողների հիմնական գործերը (հունարենից և արաբերենից լատիներեն)։ XIV դարից գիտական փոխանակման հիմնական վայրը դառնում է Բյուզանդիան։ Հատկապես մեծ եռանդով թարգմանվեցինԷ և հրատարակվեցին Էվկլիդեսի «Սկզբունքներ»-ը, այնուհետ աստիճանաբար դրանք ծավալվեցին տեղի երկրաչափների մեկնաբանություններով։ Բյուզանդիայի հետ-անտիկ պատմության միակ համեմատաբար խոշոր մաթեմատիկոսը Մաքսիմ Պլանուդն էր՝ Դիոֆանտի մեկնաբանը և տասնորդական համակարգի տարածողը։
12-րդ դարի վերջին մի քանի վանական դպրոցների բազայի վրա ստեղծվեց Փարիզի համալսարանը, որտեղ սովորում էին հազարավոր ուսանողներ ողջ Եվրոպայից։ Գրեթե միաժամանակ Բրիտանիայում հիմնվեցին Օքսֆորդը և Քեմբրիջը։ Գիտության նկատմամբ հետաքրքրությունն աճում էր, և դրա դրսևորումներից մեկը թվային համակարգի փոփոխությունն էր։ Երկար ժամանակ Եվրոպայում օգտագործվում էին հռոմեական թվերը։ XII—XIII դարերում Եվրոպայում տպագրվել են տասնորդական դիրքային համակարգի առաջին նկարագրությունները (նախ Ալ-Խվարեզմիի թարգմանությունները, ապա օգտագործման ձեռնարկները), այնուհետ սկսվել է դրա կիրառումը։ XIV դարից հնդ-արաբական թվանշանները սկսում են դուրս մղել հռոմեական թվանշաններին, նույնիսկ տապանաքարերի վրա։ Միայն աստղագիտության մեջ երկար ժամանակ օգտագործվել է վեաթսունական բաբելոնական թվաբանությունը։

XIII դարի միջնադարյան Եվրոպայի առաջին խոշոր մաթեմատիկոսը եղել է Լեոնարդո Պիզանսկին, ով հայտնի էր Ֆիբոնաչի մականունով։ Նրա հիմնական աշխատությունը՝ «Աբակոսի գիրքը» (1202, երկրորդ վերամշակված հրատարակություն - 1228)։ Լեոնարդոն աբակա անվանել է թվաբանական հաշվարկները։ Ֆիբոնաչին արաբական թարգմանություններից քաջատեղյակ էր հին մաթեմատիկոսների ձեռքբերումներին և դրանց զգալի մասը համակարգեց իր գրքում։ Նրա ներկայացումը իր ամբողջականությամբ և խորությամբ անհամեմատ բարձր էր բոլոր հին և իսլամական նախատիպերից և երկար ժամանակ անգերազանցելի էր։ Այս գիրքը հսկայական ազդեցություն ունեցավ Եվրոպայում մաթեմատիկական գիտելիքների, հնդկական թվերի և տասնորդական համակարգի տարածման վրա։
Ջորդան Նեմորարիուսի «Թվաբանություն» և «Տված թվերի մասին» գրքերում երևում են սիմվոլիկ հանրահաշվի սաղմերը՝ դեռևս երկրաչափությունից չանջատված[7]։
Միևնույն ժամանակ, Ռոբերտ Գրոսետեստը և Ռոջեր Բեկոնը առաջարկեցին ստեղծել փորձարարական գիտություն, որը կկարողանա նկարագրել բնական երևույթները մաթեմատիկական լեզվով[8]։
XIV դարում համալսարաններ են հիմնվում գրեթե բոլոր խոշոր քաղաքներում (Պրահա, Կրակով, Վիեննա, Հայդելբերգ, Լայպցիգ, Բազել և այլն)։
Օքսֆորդի Մերթոն քոլեջի փիլիսոփաները, ովքեր ապրել են 14-րդ դարում և Օքսֆորդի հաշվիչների խմիբ մաս են կազմել, մշակել են հատկությունների ուժեղացման և թուլացման տրամաբանական-մաթեմատիկական ուսմունք։ Նույն ուսմունքի մեկ այլ տարբերակ մշակվել է Սորբոնում Նիկոլաս Օրեմի կողմից։ Կախվածությունը ներկայացրեց գրաֆիկի տեսքով ուսումնասիրեց շարքերի զուգամիտությունը[9]։ Հանրահաշվական աշխատություններում նա դիտարկել է կոտորակային ցուցիչներ։
15-րդ դարի ականավոր գերմանացի մաթեմատիկոս և աստղագետ Յոհան Մյուլլերը լայնորեն հայտնի դարձավ Regiomontanus անունով, որը իր հայրենի քաղաքի Քյոնիգսբերգի անվան լատինացված տարբերակն է[C 1]։ Նա հրատարակեց հատուկ եռանկյունաչափությանը նվիրված առաջին աշխատությունը Եվրոպայում։ Արաբական աղբյուրների համեմատ՝ նորություն քիչ կար, սակայն ներկայացված էր համակարգված և ամբողջական։
Լուկա Պաչոլին, 15-րդ դարի մեծագույն հանրահաշվագետ, Լեոնարդո դա Վինչիի ընկերը, տվել է հանրահաշվական սիմվոլիզմի հստակ (թեև ոչ այնքան հարմար) ուրվագիծը։
XVI դար[խմբագրել | խմբագրել կոդը]
XVI դարը դարը շրջադարձային էր եվրոպական մաթեմատիկայի համար։ Լիովին յուրացնելով իր նախորդների նվաճումները՝ այն մի քանի հզոր ցատկերով շատ առաջ մղվեց[10]։
Առաջին խոշոր ձեռքբերումը երրորդ և չորրորդ աստիճանի հավասարումների լուծման ընդհանուր մեթոդի հայտնաբերումն էր է։ Իտալացի մաթեմատիկոսներ դել Ֆերրոն, Տարտալյան և Ֆերարին լուծեցին մի խնդիր, որից գլուխ չէին հանում աշխարհի լավագույն մաթեմատիկոսները, մի քանի դար շարունակ[11]։ Միաժամանակ պարզվել է, որ լուծումները երբեմն բացասական թվեր են։ Եվրոպացի մաթեմատիկոսներն այս արմատներն անվանեցին «երևակայական թվեր» և մշակեցին դրանց հետ գործողություններ կատարելու կանոններ։ Այս կերպ մաթեմակիայում հայտնվեցին կոմպլեքս թվերը։
1585 թվականին ֆլամանդացի Սիմոն Սթևինը հրատարակում է «Տասներորդ» գիրքը տասնորդական կոտորակներով գործողության կանոնների մասին, որից հետո տասնորդական համակարգը վերջնական հաղթանակ է տանում կոտորակային թվերի ոլորտում։ Կոտորակներ գրելիս ստորակետի օգտագործումը առաջին անգամ հանդիպել է 1592 թվականին։ Սթևինը նաև հայտարարեց ռացիոնալ և իռացիոնալ թվերի, ինչպես նաև (որոշ վերապահումներով) բացասական թվերի կատարյալ իրավահավասարությունը[12]։
Դեպի նոր մաթեմատիկա կարևորագույն քայլ է կատարել ֆրանսիացի Ֆրանսուա Վիետը։ 1591 թվականին հրատարակված իր «Վերլուծական արվեստի ներածություն» գրքում նա վերջնականապես ձևակերպեց թվաբանության սիմվոլների մետալեզուն՝ հանրահաշիվը[13]։ Հանրահաշվի ի հայտ գալով ստեղծվեց խորը և ընդհանուր հետազոտություններ կատարելու հնարավորություն։ Այս գրքում Վիետը ցույց տվեց նոր մեթոդի հզորությունը՝ դուրս բերելով Վիետայի հայտնի բանաձևերը։ Վիետի սիմվոլիկան դեռևս արդի սիմվոլիկան չէր, այն հետագայում առաջարկեց Դեկարտը[14]։
Միևնույն ժամանակ, մաթեմատիկայի հեղինակությունը մեծանում էր, և շատ գործնական խնդիրներ են ի հայտ են գալիս՝ հրետանու, նավիգացիայի, շինարարության, արդյունաբերության, հիդրոտեխնիկայի, աստղագիտության, քարտեզագրության, օպտիկայի և այլն ոլորտներում։ Ի տարբերություն հնագույն ժամանակների, Վերածննդի գիտնականները նման առաջադրանքներից չէին խուսափում։ Փաստացի, մաքուր տեսական մաթեմատիկոսներ չկային։ 16-17-րդ դարերում համալսարանական գիտության դերն ընկնում է, ի հայտ են գալիս բազմաթիվ ոչ պրոֆեսիոնալ գիտնականներ․ Սթևին - ռազմական ինժեներ, Վիետ և Ֆերմա - իրավաբաններ, Դեզարտ և Ռեն - ճարտարապետներ, Լայբնից - պաշտոնյա, Նեպեր, Դեկարտ, Պասկալ - ճարտարապետներ, Նեպեր, Դեկարտ, Պասկալ - - մասնավոր անձինք[15]։
XVII դար[խմբագրել | խմբագրել կոդը]
XVII դարում մաթեմատիկայի բուռն զարգացումը շարունակվեց, և դարավերջին գիտության դեմքը արմատապես փոխվեց։

XVII դարի առաջին մեծ հայտնագործությունը լոգարիթմների գյուտն էր։ 1614 թվականին շոտլանդացի սիրող մաթեմատիկոս Ջոն Նապիերը «Լոգարիթմների զարմանալի աղյուսակի նկարագրությունը» (lat. Mirifici Logarithmorum Canonis Descriptio) վերնագրով լատիներենով շարադրություն հրատարակեց Այն պարունակում էր լոգարիթմների և դրանց հատկությունների համառոտ նկարագրությունը, ինչպես նաև սինուսների, կոսինուսների և տանգեսների լոգարիթմների 8 նիշանոց աղյուսակներ՝ 1' քայլով։ Նեփյերի առաջարկած լոգարիթմ տերմինը հաստատվեց գիտության մեջ Նեփյերը լոգարիթմների տեսությունը նկարագրել է իր մյուս «Լոգարիթմների զարմանալի աղյուսակի կառուցում» (լատ. Mirifici Logarithmorum Canonis Constructio) գրքում, որը 1619 թվականի նհետմահու հրատարակվել է նրա որդու՝ Ռոբերտի կողմից։ Բարդ հաշվարկները բազմիցս պարզեցվել են, և մաթեմատիկան ստացել է նոր, կիրառությունների լայն շրջանակով, ոչ դասական ֆունկցիա։
Ռենե Դեկարտը իր «Երկրաչափություն» (1637) տրակտատում ուղղել է հնագույն մաթեմատիկոսների ռազմավարական սխալը և վերականգնել թվի հանրահաշվական ըմբռնումը (երկրաչափականի փոխարեն)[16]։ Ավելին, նա երկրաչափական պնդումները հանրահաշվականի ձևափոխելու միջոց առաջարկեց(օգտագործելով կոորդինատային համակարգ), որից հետո ուսումնասիրությունները, գործողությունները դրանց պարզեցվում են։ Այս կերպ է սկիզբ առել անալիտիկ երկրաչափությունը։ Դեկարտը բազմաթիվ օրինակներ դիտարկեց, որոնք ցույց տվեցին նոր մեթոդի մեծ հզորությունը և հնագույն մաթեմատիկոսներին անհայտ շատ արդյունքներ ստացավ։ Հատկապես ուշագրավ է նրա մշակած մաթեմատիկական սիմվոլիկան, որը մոտ է ժամանակակիցին։
Դեկարտի վերլուծական մեթոդը անմիջապես ընդունվեց Վալլիսի, Ֆերմայի և շատ այլ նշանավոր մաթեմատիկոսների կողմից[17]։
Պիեռ Ֆերման, Հյուգենսը և Յակոբ Բեռնուլին ստեղծեցին մաթեմատիկայի նոր ճյուղ՝ հավանականության տեսությունը, որին մեծ ապագա էր վիճակված։ Յակոբ Բեռնուլին ձևակերպեց մեծ թվերի օրենքի առաջին տարբերակը[29][18]։ Եվ, վերջապես, հայտնվեց ոչ շատ պարզ, բայց խորը գաղափար՝ կամայական հարթ կորերի վերլուծություն՝ դրանք քայքայելով ուղիղ գծերի անսահման փոքր հատվածների։

Եվ, վերջապես, հայտնվեց ոչ շատ հստակ, բայց խորը գաղափար՝ կամայական հարթ կորերի վերլուծություն՝ դրանք տրոհելով անսահման փոքր հատվածների։ Այս գաղափարի առաջին իրականացումը անբաժանելիների, ընդհանուր առմամբ ոչ կատարյալ, մեթոդն էր (Կեպլեր[19], Կավալիերի[20], Ֆերմա[21]), և արդեն նրա օգնությամբ բազմաթիվ նոր բացահայտումներ արվեցին։ 17-րդ դարի վերջին անբաժանելիների գաղափարը զգալիորեն ընդլայնվեց Նյուտոնի[22] և Լայբնիցի[23] կողմից և հայտնվեց բացառիկ հզոր հետազոտական գործիք՝ մաթեմատիկական անալիզը։ Այս մաթեմատիկական ուղղությունը դարձավ հիմնականը հաջորդ՝ XVIII դարում
Բացասական թվերի տեսությունը դեռևս կայացման փուլում էր։ Օրինակ, բուռն քննարկվում էր տարօրինակ համամասնությունը —որտեղ ձախից առաջին անդամը մեծ է երկրորդից, իսկ աջից՝ հակառակը, ստացվում է, որ մեծը հավասար է փոքրին («Առնոյի պարադոքս»)[24]։
Կոմպլեքս թվերը համարվում էին մտացածին, դրանց հետ վարվելու կանոնները վերջնականապես չէին մշակվել։ Ավելին, պարզ չէր, թե արդյոք բոլոր «կեղծ թվերը» կարելի է ներկայացնել «a + bi» տեսքով, թե, ասենք, որոշակի արմատ հանելիս կարող են հայտնվել այլ տարբերակներ, որոնք չեն կարող կրճատվել այս ձևի վրա ( նույնիսկ Լայբնիցն էր այդպես կարծում)։ Միայն 18-րդ դարում Դ'Ալամբերը և Էյլերը հաստատեցին, որ կոմպլեքս թվերը փակ են բոլոր գործողությունների նկատմամբ, ներառյալ ցանկացած աստիճանի արմատ հանելը։
Во второй половине XVII դարի երկրորդ կեսին հայտնվեցին գիտական պարբերականներ, որոնք դեռևս մասնագիտացված չէին գիտությունների ճյուղերի մեջ։ Սկիզբը դրեցին Լոնդոնն ու Փարիզը, սակայն հատկապես կարևոր դեր է խաղացել Acta Eruditorum (1682, Լայպցիգ, լատիներենով)։ 1699 թվականից Ֆրանսիայի գիտությունների Ակադեմիան հրատարակում է իր գրառումները (Հուշերը)։ Այս ամսագրերը հազվադեպ էին տպագրվում, և նամակագրությունը գիտնականների միջև շարունակում էր մնալ տեղեկատվության տարածման անփոխարինելի միջոց։
XVIII դար[խմբագրել | խմբագրել կոդը]
XVIII դարը մաթեմատիկայում կարելի է համառոտ բնութագրել որպես մաթանալիզի դար, որը դարձավ մաթեմատիկոսների ջանքերի կիրառման հիմնական առարկան։ Բնական գիտությունների բուռն զարգացմանը նպաստելուն զուգահեռ մաթանալիզը իր հերթին առաջադիմեց՝ դրանցից ստանալով ավելի ու ավելի բարդ առաջադրանքներ։ Այս գաղափարների համատեղմամբ ծնվեց մաթեմատիկական ֆիզիկան։
Նոր մոտեցման հաղթական հաջողությունների ճնշման ներքոԱ, անվերջ փոքրերի մեթոդի քննադատությունը, որի պատճառը դրա վատ հիմնավորումն էր տեղի տվեց։ Ի շնորհիվ Նյուտոնի գիտության մեջ իշխում էր մեխանիկան, մնացած բոլոր փոխազդեցությունները համարվում էին մեխանիկական գործընթացների հետևանքներ։ Մաթանալիզի և մեխանիկայի զարգացումը տեղի էր ունենում սերտ միահյուսմամբ։ Այս միավորումն առաջինն իրականացրեց Էյլերը, ով հանեց արխայիկ կոնստրուկցիաները Նյուտոնյան մեխանիկայից հեռացրեց արխայիկ կոնստրուկցիաները և դինամիկայի տակ անալիտիկ հիմք դրեց(1736 թ.)։ Այդ պահից ի վեր մեխանիկան դարձավ մաթանալիզի կիրառական ճյուղ։ Գործընթացն ավարտեց Լագրանժը, ում «Անալիտիկ մեխանիկան»[25] ցուցադրաբար ոչ մի գծագիր չի պարունակում։ Միաժամանակ մաթանալիզը հանրահաշվականացավ և վերջնականապես (սկսած Էյլերից) առանձնացավ երկրաչափությունից ու մեխանիկայից։
Բնության ճանաչման հիմնական մեթոդը դառնում է դիֆերենցիալ հավասարումների կազմումն ու լուծումը։ Կետի դինամիկայից հետո հերթը հասավ կոշտ մարմնի, ապա հեղուկի և գազի դինամիկային։ Այս ոլորտում առաջընթացին մեծապես նպաստեց լարի շուրջ վեճը, որին մասնակցում էին Եվրոպայի առաջատար մաթեմատիկոսները։
Նյուտոնի ձգողականության տեսությունը լուսնի շարժումը նկարագրելում ի սկզբանե դժվարությունների հանդիպեց, սակայն Կլարաուտի, Էյլերի և Լապլասի աշխատանքը[26] հստակ ցույց տվեց, որ երկնային մեխանիկայի մեջ Նյուտոնյանից բացի այլ լրացուցիչ ուժեր չկան։
Մաթանալիզը տարածվում է կոմպլեքս թվերի վրա։ Ֆունկցիաների մեծ մասի անալիտիկ շարունակությունը խնդիրներ չէր առաջացնում, և ստանդարտ ֆունկցիաների միջև անսպասելի կապեր են հայտնաբերվել (Էյլերի ֆորմուլա)[27]։ Դժվարություններ ծագեցին կոմպլեքս լոգարիթմի դեպքում, բայց Էյլերը հաջողությամբ դրանք հաղթահարեց։ Ներմուծվեցին կոնֆորմ արտապատկերումները, առաջ քաշվեց անալիտիկ շարունակության եզակիության հիպոթեզը։ Կոմպլեքս ֆունկցիաները նույնիսկ իրենց կիրառումը գտան կիրառական գիտություններում՝ հիդրոդինամիկա, տատանումների տեսություն (Դալամբեր, Էյլեր)։
Շատ առաջադիմեցին ինտեգրման տեսությունն ու տեխնիկան։ Լայն կիրառություն են ստանում բազմակի ինտեգրալները (Էյլեր, Լագրանժ), ընդ որում ոչ միայն դեկարտյան կոորդինատներում։ Հայտնվում են նաև մակերևույթային ինտեգրալներ (Լագրանժ, Գաուս)։ Ուժգին զարգանում է դիֆերենցիալ հավասարումների տեսությունը՝ ինչպես սովորական և այնպես և մասնակի։ Մաթեմատիկոսները բացառիկ հնարամտություն են ցուցաբերում մասնակի դիֆերենցիալ հավասարումներ լուծելիս՝ յուրաքանչյուր խնդրի լուծման համար, նոր մեթոդները հորինելով։ Ձևակերպվեց սահմանային արժեքի խնդրի հասկացությունը, և ի հայտ եկան դրա լուծման առաջին մեթոդները։
XVIII դարի վերջում սկիզբ է առել պոտենցիալի ընդհանուր տեսությունը (Լագրանժ, Լապլաս, Լեժանդր). Ձգողականության համար պոտենցիալը ներմուծել է Լագրանժը (1773, տերմինն առաջարկել է Գրինը 1828 թվականին)։ Շուտով Լապլասը պոտենցիալի և Լապլասի հավասարման միջև կապ հայտնաբերեց և ներկայացրեց օրթոգոնալ գնդային ֆունկցիաների կարևոր դաս։
Ի հայտ են գալիս շատ խոստումնալից վարիացիոն հաշիվը և ֆիզիկայի վարիացիոն սկզբունքները (Էյլեր, Լագրանժ)։

XVIII դարում մաթեմատիկոսների առաջատարը Էյլերն էր, ում բացառիկ տաղանդը իր հետքը թողեց դարի բոլոր հիմնական մաթեմատիկական նվաճումների վրա[28]։ Հենց նա էր, ով մաթանալիզը դարձրեց կատարյալ հետազոտական գործիք։ Էյլերը զգալիորեն հարստացրեց ֆունկցիաների տեսականին, մշակեց ինտեգրման տեխնիկան և փաստացի առաջ տարավ մաթեմատիկայի գրեթե բոլոր ճյուղերը։ Պիեռ Լուի դը Մոպերտյուի հետ զուգահեռ, նա ձևակերպեց նվազագույն գործողության սկզբունքը՝ որպես բնության ամենաբարձր և համընդհանուր օրենք։ Наряду с Թվերի տեսության մեջ կեղծ թվերը վերջնականապես օրինականացվում են, թեև դրանց ամբողջական տեսությունը դեռ չէր ստեղծվել։ Հանրահաշվի հիմնական թեորեմն ապացուցված է (դեռևս ոչ լիովին խիստ)։ Էյլերը մշակեց ամբողջ թվերի բաժանելիության տեսությունը և համեմատությունների (մնացորդների) տեսությունը, որն ավարտվին հասցրեց Գաուսը։ Էյլերը և Լագրանժը հրատարակեցին շղթայական կոտորակների ընդհանուր տեսությունը, և դրա օգնությամբ նրանք լուծեցին դեոֆանտյան անալիզի բազմաթիվ խնդիրներ։ Էյլերը նաև պարզել է, որ մաթանալիզի մեթոդները կարող են կիրառվել թվերի տեսության մի շարք խնդիրների դեպքում։
Սրընթաց զարգանում էր գծային հանրահաշիվը։ Գծային համակարգերի ընդհանուր լուծման առաջին մանրամասն նկարագրությունը 1750 թվականին տվել է Գաբրիել Կրամերը։ Ժամանակակից սիմվոլիկային մոտ, որոշիչների խորը վերլուծություն է արել Ալեքսանդր Թեոֆիլուս Վանդերմոնդը (1735—1796)։ 1772 թվականին Լապլասը տվել է որոշիչի տրոհումը մինորների։ Դետերմինանտների տեսությունը շատ արագ կիրառություն գտավ աստղագիտության և մեխանիկայի մեջ (աշխարհիկ հավասարում), հանրահաշվական համակարգերի լուծման, ձևերի ուսումնասիրության և այլնի մեջ։
Հանրահաշվում նոր գաղափարներ են հասունանում, որոնք արդեն 19-րդ դարում իրենց գագաթնակետին են հասնում Գալուայի տեսության և վերացական կառուցվածքների տեսքով։ Հինգ և ավելի բարձր աստիճանի հավասարումների ուսումնասիրության ժամանակ Լագրանժը մոտենում է Գալուայի տեսությանը (1770), պարզելով, որ «հավասարումների իսկական մետաֆիզիկան, դա տեղափոխումների տեսությունն է»։ Երկրաչափության մեջ հայտնվում են նոր բաժիններ՝ կորերի և մակերեսների դիֆերենցիալ երկրաչափություն, գծագրական երկրաչափություն (Մոնժ), պրոյեկտիվ երկրաչափություն (Լազար Կառնո)։

Հավանականության տեսությունը դադարում է էկզոտիկ լինել և ապացուցում է իր օգտակարությունը մարդկային գործունեության ամենաանսպասելի ոլորտներում։ Մուավրը և Դանիել Բեռնուլին հայտնաբերում են նորմալ բաշխումը։ Ի հայտ են գալիս հավանական սխալի տեսությունը և գիտական վիճակագրությունը։ Հավանականությունների տեսության զարգացման դասական փուլն ավարտվեց Լապլասի աշխատություններով[29]։ Այնուամենայնիվ, դրա կիրառությունները ֆիզիկայում գրեթե բացակայում էին (չհաշված սխալների տեսությունը)։ Մաթեմատիկական հետազոտությունների կենտրոններ են դառնում Գիտությունների ակադեմիաները՝ հիմնականում պետական։ Բուհերի կարևորությունը ցածր էր (բացառությամբ այն երկրների, որտեղ դեռ ակադեմիաներ չկային), դեռևս բացակայում էին ֆիզիկայի և մաթեմատիկայի բաժինները։ Առաջնակարգ դեր էր խաղում Փարիզի ակադեմիան։ Անգլիական դպրոցը Նյուտոնից հետո առանձնանում է և գիտական մակարդակը մի դարով ետ գցում։ XVIII դարի Անգլիայի նշանավոր մաթեմատիկոսների թիվը փոքր էր. դը Մոյրը (ֆրանսիացի հուգենոտ էմիգրանտ), Կոտսը, Թեյլորը, ՄաքԼորինը, Ստիռլինգը։ Մաթեմատիկոսները դառնում են պրոֆեսիոնալներ, սիրող մաթեմատիկոսները գրեթե անհետանում են ասպարեզից։
XVIII դարի վերջում մասնագիտացված մաթեմատիկական ամսագրեր ի հայտ եկան, մեծացավ հետաքրքրությունը գիտության պատմության նկատմամբ։ Լույս է տեսնում Մոնթուկլայի «Մաթեմատիկայի պատմություն» երկհատորյակը (հետմահու վերահրատարակվել և ընդլայնվել է մինչև 4 հատոր)։ Ընդլայնվում է գիտահանրամատչելի գրականության հրատարակչությունը։
XIX դար[խմբագրել | խմբագրել կոդը]
Բնական գիտություններում մաթեմատիկայի կիրառման անհերքելի արդյունավետությունը գիտնականներին դրդեց մտածել, որ մաթեմատիկան, այսպես ասած, ներկառուցված է տիեզերքի մեջ, նրա իդեալական հիմքն է։ Այլ կերպ ասած, մաթեմատիկական գիտելիքը իրական աշխարհի իմացության մաս է կազմում։ XVII—XVIII դարերի շատ գիտնականներ դրանում չէին էլ կասկածում։ Սակայն XIX դարում մաթեմատիկայի էվոլյուցիոն զարգացումը խաթարվեց, և այդ, անսասան թվացող թեզը, կասկածի տակ առնվեց։

- Երկրաչափության, հանրահաշվի, մաթանալիզի մեջ ի հայտ են գալիս ոչ սովորական հատկություններով բազմաթիվ ոչ ստանդարտ կառուցվածքներ՝ ոչ էվկլիդեսյան և բազմաչափ երկրաչափություններ, քվատերնիոններ, վերջավոր դաշտեր, ոչ կոմուտատիվ գործողություններ, խմբեր և այլն։
- Ավելի հաճախ մաթեմատիկական հետազոտության առարկա են դառնում ոչ թվային օբյեկտները՝ պատահարներ, պրեդիկատներ, բազմություններ, աբստրակտ կառուցվածքներ, վեկտորներ, տենզորներ, մատրիցաներ, ֆունկցիաներ, բազմագծային ձևեր և այլն։
- Ի հայտ է գալիս մաթեմատիկական տրամաբանությունը և մեծ զարգացում է ապրում, ինչը մաթեմատիկայի հիմքերը դրա հետ կապելու գայթակղություն է առաջացնում։
- Գեորգ Կանտորը մաթեմատիկայի մեջ ներմուծում է չափազանց վերացական բազմությունների տեսություն, և միևնույն ժամանակ կամայական մասշտաբի իրական անսահմանության հասկացությունը։ Դարավերջին, երբ մաթեմատիկայի հիմքը փորձում էին հիմնավորել բազմությունների տեսության հիման վրա, բացահայտվեցին հակասություններ, որոնք ստիպեցին մտածել բարդ հարցերի շուրջ՝ ի՞նչ են նշանակում «գոյություն» և «ճշմարտություն» մաթեմատիկայում։
Ընդհանուր առմամբ, XIX դարում մաթեմատիկայի դերն ու հեղինակությունը գիտության և տնտեսագիտության մեջ նկատելիորեն աճեց, և համապատասխանաբար աճեց նաև դրա պետական աջակցությունը։ Մաթեմատիկան կրկին դառնում է մեծամասամբ համալսարանական գիտություն։ Ստեղծվում են առաջին մաթեմատիկական ընկերությունները՝ լոնդոնյան, ամերիկյան, ֆրանսիական, մոսկովյան, ինչպես նաև ընկերություններ Պալերմոյում և Էդինբուրգում։
Համառոտ դիտարկենք մաթեմատիկայի հիմնական ճյուղերի զարգացումը 19-րդ դարում։
Երկրաչափություն[խմբագրել | խմբագրել կոդը]
Եթե XVIII դարը մաթանալիզի դար էր, ապա XIX դարը առավելապես դարձավ երկրաչափության դար[30]։ Արագ զարգանում էին XVIII դարի վերջում ստեղծված գծագրական երկրաչափությունը (Մոնժ[31], Լամբերտ) և վերածնված պրոյեկտիվ երկրաչափությունը (Մոնժ, Պոնսելե, Լազար Կառնո)։ Ի հայտ են գալիս նոր բաժիններ՝ Վեկտորական հաշիվ, Լոբաչևսկու երկրաչափություն, Ռիմանի երկրաչափություն, հոմոմորֆ խմբերի տեսություն։ Տեղի է ունենում երկրաչափության ինտենսիվ հանրահաշվականացում, այնտեղ են թափանցում խմբերի տեսության մեթոդները, ծնվում է հանրահաշվական երկրաչափությունը։ Դարավերջին ստեղծվեց «որակական երկրաչափություն»՝ տոպոլոգիա։

Գաուսի չափազանց բովանդակալից «Ընդհանուր հետազոտություններ կոր մակերևույթների վերաբերյալ» (1822)[32] աշխատության հրապարակումից հետո, դիֆերենցիալ երկրաչափությունը հզոր խթան ստացավ։ Աշխատությունում առաջին անգամ հստակ սահմանված էր մետրիկան (առաջին քառակուսի ձևը) և դրա հետ կապված մակերևույթի ներքին երկրաչափությունը։ Հետազոտությունը շարունակեց փարիզյան դպրոցը։ 1847 թվականին Ֆրենեն և Սերետը հրապարակեցին Ֆրենեի հայտնի բանաձևերը կորի դիֆերենցիալ հատկանիշների համար[33]։
Մեծագույն ձեռքբերումը վեկտորի և վեկտորական դաշտի ներմուծումն էր։ Սկզբում վեկտորները առաջ բերեց Ու.Համիլտոնը՝ կապված իր Քվատերնիոնների հետ (որպես դրանց եռաչափ երևակայական մաս)։ Համիլտոնը արդեն իսկ կային սկալյար և վեկտորական արտադրյալները։ Ավելին, նա ներմուծեց դիֆերենցիալ օպերատորը՝ («նաբլա») և վեկտորային անալիզի շատ այլ հասկացություններ, այդ թվում վեկտոր ֆունկցիայի սահմանումը և տենզորային արտադրյալը։
Մաքսվելի առաջին աշխատություններում օգտագործած վեկտորական սիմվոլիկայի կոմպակտությունն ու ինվարիանտությունը հետաքրքրեց ֆիզիկոսներին և շուտով հրատարակվեցին Գիբսի «Վեկտորական անալիզի տարրերը» (1880-ականներ), ավելի ուշ Հևիսայդը (1903) վեկտորական հաշիվը բերեց ժամանակակից տեսքին։
Պրոյեկտիվ երկրաչափությունը, մեկուկես դար մոռացությունից հետո, կրկին ուշադրության արժանացավ, նախ Մոնժի, ապա նրա ուսանողներ Պոնսլեի և Լազար Կարնոյի կողմից։ Կարնոն ձևակերպեց «շարունակականության սկզբունքը», որը թույլ է տալիս անմիջապես սկզբնական պատկերի որոշ հատկությունները անմիջապես տարածել շարունակական փոխակերպմամբ դրանից ստացված պատկերներին (1801-1806) Որոշ ժամանակ անց Պոնսելեն հստակ սահմանեց պրոյեկտիվ երկրաչափությունը՝ որպես պատկերների պրոյեկտիվ հատկությունների գիտություն և տվեց դրա սիստեմատիկ նկարագրությունը (1815 թ.)։
1820-ական թվականների վերջից Գերմանիայում ձևավորվում է պրոյեկտիվ երկրաչափերի դպրոց (Մյոբիուս, Պլյուկեր, Հեսսեն, Շտայներ և ուրիշներ)։ Անգլիայում մի շարք աշխատություններ հրատարակեց Քելին։ Ընդ որում, սկսեցին կիրառվել անալիտիկ մեթոդներ, հատկապես Մոբիուսի կողմից միատարր պրոյեկտիվ կոորդինատների հայտնաբերումից հետո։ Ֆրանսիայում Պոնսլեի աշխատանքները շարունակեց Միշել Շալը։
Մաթեմատիկայի զարգացման վրա մեծ ազդեցություն ունեցավ «Երկրաչափության հիմքում ընկած հիպոթեզների մասին» Ռիմանի հայտնի ելույթը (1854)[34]։

XIX դարի վերջում վերջապես ընդհանուր ուշադրությունը գրավեց Լոբաչևսկու երկրաչափությունը։ Փաստը, որ նույնիսկ դասական երկրաչափությունն ունի այլընտրանք, հսկայական ազդեցություն ունեցավ ողջ գիտական աշխարհի վրա։ Այն նաև խթանեց մաթեմատիկայի և ֆիզիկայի բազմաթիվ հաստատված կարծրատիպերի վերագնահատումը։
Երկրաչափության զարգացման համար շրջադարձային էր նաև 1872 թվականը, երբ Ֆելիքս Քլայնը ներկայացրեց իր «Էրլանգեն ծրագիրը»։ Նա երկրաչափության ճյուղերը դասակարգել է ըստ օգտագործվող ձևափոխումնռրի խմբի՝ պտույտներ, աֆինային, պրոյեկտիվ, ընդհանուր շարունակական և այլն։ Երկրաչափության յուրաքանչյուր ճյուղ ուսումնասիրում է ձևափոխությունների համապատասխան խմբի ինվարիանտները։ Քլայնը նաև դիտարկել է իզոմորֆիզմի (կառուցվածքային նույնության) հասկացությունը, որը նա անվանել է «տեղափոխություն»։ Այսպիսով, ուրվագծվեց երկրաչափության հանրահաշվականացման մի նոր փուլ՝ երկրորդը՝ Դեկարտից հետո։
1872—1875 թվականներին Կամիլ Ժորդանը անալիտիկ երկրաչափության՝ n-չափ տարածության (կորեր և մակերեսներ), մի շարք հոդվածներ հրապարակեց, իսկ դարավերջում նա առաջարկեց ընդհանուր չափումների տեսությունը։

Դարավերջին ծնվեց տոպոլոգիան՝ սկզբում analysis situs անվան տակ։ Տոպոլոգիական մեթոդներն փաստացի օգտագործվել են Էյլերի, Գաուսի, Ռիմանի, Ջորդանի և այլոց մի շարք աշխատություններում։ Ֆելիքս Քլայնը նոր գիտության թեման բավականին հստակ նկարագրում է իր «Էրլանգեն ծրագրում»։ Կոմբինատոր տոպոլոգիան վերջնականապես ձևավորվեց Պուանկարեի (1895-1902) աշխատություններում։
Մաթեմատիկական անալիզ[խմբագրել | խմբագրել կոդը]
XIX դարում մաթանալիզը արագ, խաղաղ էվոլյուցիոն ճանապարհով։

Ամենաէական փոփոխությունը անալիզի հիմքը ստեղծելն էր (Կոշի, այնուհետ Վեյերշտրաս)։ Կոշիի[35] շնորհիվ փաստացի անվերջ փոքրի միստիկական հասկացությունն անհետացավ մաթեմատիկայից (չնայած այն դեռևս օգտագործվում է ֆիզիկայում)։Տարամիտող շարքերի հետ կասկածելի գործողությունները նույնպես գիտությունից դուրս մղվեցին։ Կոշին մաթանալիզ հիմքը կառուցեց նյուտոնյան ըմբռնմանը մոտ՝ սահմանների տեսության հիման վրա։ Նրա մոտեցումը ընդունվեց և մաթանալիզը դարձավ ավելի քիչ հանրահաշվական, բայց ավելի հուսալի։ Այնուամենայնիվ, մինչ Վայերշտրասի ճշգրտումները շատ նախապաշարմունքներ դեռևս պահպանվում էին. օրինակ, Կոշին կարծում էր, որ անընդհատ ֆունկցիան միշտ ածանցելի է, իսկ անընդհատ ֆունկցիաների գումարը անընդհատ է։
Ամենալայն զարգացում է ստացել կոմպլեքս փոփոխականի անալիտիկ ֆունկցիաների տեսությունը, որի վրա աշխատել են Լապլասը, Կոշին, Աբելը, Լուիվիլը, Յակոբին, Վայերշտրասը և ուրիշներ։ Զգալիորեն ընդլայնվել է կոմպլեքս ֆունկցիաների դասը։ Հիմնական ջանքերն ուղղված էին Աբելյան ֆունկցիաների տեսությանը, որը սակայն, միայն նպաստեց 20-րդ դարում անալիտիկ գործիքների հարստացմանը և ավելի ընդհանուր տեսությունների ստեղծմանը։
Բազմաթիվ կիրառական խնդիրներ գործնականում խթանեցին դիֆերենցիալ հավասարումների տեսությունը։ Մանրակրկիտ ուսումնասիրվել են մաթեմատիկական ֆիզիկայի հիմնական հավասարումները, ապացուցվել են լուծումների գոյության թեորեմները, ստեղծվել է դիֆերենցիալ հավասարումների բարձրակարգ տեսություն (Պուանկարե)։ դարավերջում տեղի է ունեցել անալիզի որոշակի երկրաչափականացում՝ առաջացել է վեկտորային անալիզ, տենզորային անալիզ, ուսումնասիրվել են անսահման ֆունկցիաների տարածություններ (տես Բանախի տարածություն, Հիլբերտյան տարածություն)։
Հանրահաշիվ և թվերի տեսություն[խմբագրել | խմբագրել կոդը]
Էյլերի անալիտիկ մեթոդները օգնեցին լուծել թվերի տեսության բազմաթիվ բարդ խնդիրներ (Գաուս[36], Դիրիխլե և այլոք)։ Գաուսը տվեց հանրահաշվի հիմնարար թեորեմի առաջին անբասիր ապացույցը։ Ժոզեֆ Լուիվիլը ապացուցեց անսահման թվով տրանսցենդենտ թվերի գոյությունը (1844թ., ավելի մանրամասն՝ 1851թ.), տվեց տրանսցենդենտալության բավարար պայմանը և այդպիսի թվերի օրինակներ կառուցեց շարքի գումարի տեսքով։ 1873 թվականին Չարլզ Էրմիտը հրապարակեց Էյլերի e թվի տրանսցենդենտալության ապացույցը, իսկ 1882 թվականին Լինդեմանը նմանատիպ մեթոդ կիրառեց թվի նկատմամբ։

Ուիլյամ Համիլտոնը հայտնաբերեց քվատերնիոնների ոչ կոմուտատիվ աշխարհը։
Առաջ եկավ երկրաչափական թվերի տեսությունը (Մինկովսկի)[37]։
Էվարիստ Գալուան, իր ժամանակից առաջ ընկնելով, ներկայացնում է կամայական աստիճանների հավասարումների լուծման խորը վերլուծություն[38]։։

Գալուայի գաղափարների յուրացման չափին համապատասխան, դարի երկրորդ կեսից աբստրակտ հանրահաշիվը արագ զարգացավ։ Ժոզեֆ Լիուվիլը հրապարակեց Գալուայի աշխատանքը իր մեկնաբանություններով հանդերձ։ 1850-ականներին Քելին ներկայացրեց աբստրակտ խմբի գաղափարըը։ «Խումբ» տերմինը դառնում է ընդհանուր ընդունված և ներթափանցում մաթեմատիկայի գրեթե բոլոր ճյուղեր, իսկ 20-րդ դարում՝նաև ֆիզիկայի և բյուրեղագիտության մեջ։
Ձևավորվում է գծային տարածություն հասկացությունը (Գրոսման և Քելի, 1843-1844)։ 1858 թվականին Քելին հրապարակեց մատրիցների ընդհանուր տեսությունը, սահմանեց գործողություններ դրանց վրա և ներկայացրեց բնորոշ բազմանդամ հասկացությունը։ Մինչև 1870 թվականը գծային հանրահաշվի բոլոր հիմնական թեորեմներն ապացուցված էին։
1871 թվականին Դեդեկինդը ներմուծեց օղակ, մոդուլ և իդեալ հասկացությունները։ Նա և Քրոնեկերը ստեղծեցին բաժանելիության ընդհանուր տեսությունը։
XIX դարի վերջում մաթեմատիկայում հայտնվում են Լի խմբերը։
Հավանականությունների տեսություն[խմբագրել | խմբագրել կոդը]

Առաջին տեղում են սխալների տեսությունը, վիճակագրությունը և ֆիզիկական կիրառությունը։ Դրանով զբաղվել են Գաուսը, Պուասոնը, Կոշին։ Բացահայտվեց նորմալ բաշխման կարևորությունը շատ իրական իրավիճակներում, որպես սահմանային։
Բոլոր զարգացած երկրներում ստեղծվում են վիճակագրական բաժիններ։ Կառլ Փիրսոնի աշխատանքի շնորհիվ ի հայտ է գալիս մաթեմատիկական վիճակագրությունը, հիպոթեզների փորձարկմամբ և պարամետրերի գնահատմամբ։
Այնուամենայնիվ, 19-րդ դարում հավանականությունների տեսության մաթեմատիկական հիմքերը դեռևս չէին ստեղծվել, և Հիլբերտը 20-րդ դարի սկզբին այս ուղղությունը վերագրեց կիրառական ֆիզիկային[39]։
Մաթեմատիկական տրամաբանություն[խմբագրել | խմբագրել կոդը]
Լայբնիցի «Համընդհանուր բնութագրում» նախագծի ձախողումից հետո մեկուկես դար անցավ, մինչև տրամաբանության հանրահաշիվ ստեղծելու նոր փորձ արվեց Նոր փորձը նոր՝ Ճշմարտության բազմություն, հայեցակարգի վրա արվեց հնարավորություն տվեց մաթեմատիկական տրամաբանությունը կառուցելորպես՝ բազմությունների նկատմամբ գործողություններով, դասերի տեսություն։ Առաջատարներն էին բրիտանացի մաթեմատիկոսներ Օգյուստ (Օգոստոս) դե Մորգանը և Ջորջ Բուլը։

«Ձևական տրամաբանություն» (1847) աշխատանքի մեջ Մորգանը նկարագրել է ունիվերսումի հասկացողությունը և տրամաբանական գործողությունների սիմվոլները, թղթին հանձնեց նաև «Մորգանի օրենքները». Ավելի ուշ նա ներմուծեց մաթեմատիկական հարաբերության հասկացողությունը և դրանց նկատմամբ գործողությունները։
Ջորջ Բուլը ինքնուրույն մշակեց տեսության իր սեփական, ավելի հաջող տարբերակը։ 1847-1854 թվականների իր աշխատություններում նա դրել է ժամանակակից մաթեմատիկական տրամաբանության հիմքերը և նկարագրել տրամաբանության հանրահաշիվը (Բուլյան հանրահաշիվ)։ Հայտնվեցին առաջին տրամաբանական հավասարումները, ներդրվեց բաղադրիչ հասկացությունը (տրամաբանական բանաձևի տրոհում)։
Ուիլյամ Սթենլի Ջևոնսը շարունակեց Բուլի համակարգը և նույնիսկ կառուցեց «տրամաբանական մեքենա», որը կարող էր լուծել տրամաբանական խնդիրներ[40]։ 1877 թվականին Էռնեստ Շրյոդերը ձեւակերպեց երկակիության տրամաբանական սկզբունքը։ Այնուհետև Գոտլոբ Ֆրեգեն կառուցեց ասույթների հաշիվ, Չարլզ Պերսը 19-րդ դարի վերջում նկարագրեց հարաբերությունների և առաջարկային ֆունկցիաների ընդհանուր տեսությունը, ինչպես նաև ներմուծեց քվանտորներ։ Սիմվոլիկայի ժամանակակից տարբերակն առաջարկել է Պեանոն։ Դրանից հետո ամեն ինչ պատրաստ էր Հիլբերտի դպրոցում ապացույցների տեսության զարգացման համար։
Մաթեմատիկայի հիմնավորում[խմբագրել | խմբագրել կոդը]
XIX դարի սկզբին միայն էվկլիդեսյան երկրաչափությունն ուներ համեմատաբար խիստ` տրամաբանական (դեդուկտիվ) հիմնավորում, թեև նույնիսկ այն ժամանակ դրա խստությունը իրավամբ համարվում էր անբավարար։ Նոր հասկացությունների հատկությունները (օրինակ՝ կոմպլեքս թվեր, անվերջ փոքրեր և այլն) պարզապես համարվում էին, որ նույնն են, ինչ արդեն հայտնի նմանատիպ հասկացությունների հատկությունները. եթե նման էքստրապոլյացիա անհնար էր, հատկությունները ընտրվում էին էմպիրիկ եղանակով։

Մաթեմատիկայի հիմքի ստեղծումը սկսվեց անալիզիից։ 1821 թվականին հրապարակեց «Հանրահաշվական անալիզը», որտեղ նա գլխավոր գաղափարները հստակ սահմանեց սահման հասկացության հիման վրա։ Այնուամենայնիվ նա մի շարք սխալներ թույլ տվեց, օրինակ, նա առանց ապացուցելու գործողությունների թույլատրելիությունը, անդամ առ անդամ դիֆերենցեց և ինտեգրեց շարքերը։ Անալիզի հիմքը ավարտին հասցրեց Վեյերշտրասը, ով բացահայտեց կարևոր հասկացության՝ հավասարաչափ անընդհատության, դերը։ Միևնույն ժամանակ, Վայերշտրասը (1860-թվեր) և Դեդեկինդը (1870-ականներ) տվեցին իրական թվերի հիմնավորումը։
1837. Ուիլյամ Համիլտոնը կառուցում է կոմպլեքս թվերի մոդել՝ որպես իրականների զույգեր։
1870-ականներին օրինականացվել են ոչ էվկլիդեսյան երկրաչափությունները։ Էվկլիդեսյան տարածության վրա հիմնված նրանց մոդելները ապացուցեցին, որ իրենք նույնքան հակասելի չեն, որքան Էվկլիդեսի երկրաչափությունը։
1879 թվականին Ֆրեգեն հրապարակում է մաթեմատիկական տրամաբանության աքսիոմների համակարգը։
1888 թվականին Դեդեկինդն առաջարկեց բնական թվերի աքսիոմների համակարգի ուրվագիծը։ Մեկ տարի անց Պեանոն առաջարկեց աքսիոմների ամբողջական համակարգ։
1899 թվականին լույս է տեսնում Հիլբերտի Երկրաչափության հիմունքները։
Արդյունքում, դարավերջին գրեթե ողջ մաթեմատիկան կառուցվել է խիստ աքսիոմատիկայի հիման վրա։ Խստորեն ապացուցվել է մաթեմատիկայի հիմնական ճյուղերի (բացառությամբ թվաբանության) անհակասելիությունը (ավելի ճիշտ՝ բերվել է թվաբանության անհակասելիության)։ Հավանականությունների տեսության և բազմությունների տեսության աքսիոմատիկ հիմքը հայտնվեց ավելի ուշ՝ 20-րդ դարում։
Բազմությունների տեսություն և անտինոմիաներ[խմբագրել | խմբագրել կոդը]

1873 թվականին Գեորգ Կանտորը ներմուծեց կամայական թվային բազմության, այնուհետ բազմության՝ մաթեմատիկայում ամենաաբստրակտ, հասկացությունը, ընդհանուր առմամբ։ Փոխադարձ միարժեք արտապատկերումների միջոցով, նա ներմուծեց հավասար հզորության գաղափարը, այնուհետ սահմանեց հզորությունների համեմատությունը՝ փոքր, մեծ և ի վերջո բազմությունները դասակարգեց ըստ հզորության՝ վերջավոր, հաշվելի, կոնտինիում և այլն։
Հզորությունների հիերարխիան Կանտորը դիտարկում էր որպես ամբողջ թվերի հիերարխիայի (կարգի) շարունակություն (տրանսֆինիտ թվեր)։ Այսպիսով, փաստացի անսահմանությունը ներմուծվեց մաթեմատիկա, հասկացություն, որից նախկին մաթեմատիկոսները ամեն կերպ խուսափում
Սկզբում բազմությունների տեսությունը բրեհաճ ընդունվեց շատ մաթեմատիկոսների կողմից։ Այն օգնեց ընդհանրացնել ժորդանյան չափումների տեսությունը, հաջող կիրառվում էր Լեբեգի ինտեգրալների տեսության մեջ և շատերի կողմից դիտարկվում էր որպես ողջ մաթեմատիկայի ապագա աքսիոմատիկայի հիմք։ Սակայն հետադա իրադարձությունները ցույց տվեցին որ սովորական տրամաբանությունը տեղին չէ անսահմանության ուսումնասիրության համար, և ինտուիցիան միշտ չէ, որ օգնում է ճիշտ ընտրություն կատարել։
Առաջին հակասությունը ի հայտ եկավ ամենամեծ հավաքածուն՝ բոլոր բազմությունների բազմությունը (1895) դիտարկելիս։ Այն հեռացվեց մաթեմատիկայից՝ որպես անընդունելի։ Սակայն ի հայտ եկան նաև այլ հակասություններ (անտինոմներ)։

Անրի Պուանկարեն, ով սկզբում ընդունել է բազմությունների տեսությունը և նույնիսկ օգտագործել այն իր հետազոտության մեջ, հետագայում կտրականապես մերժել է այն և անվանել «մաթեմատիկայի լուրջ հիվանդություն»։ Այնուամենայնիվ, մաթեմատիկոսների մեկ այլ խումբ, ներառյալ Բերտրան Ռասելը, Հիլբերտը և Հադամարդը, պաշտպանեցին «կանտորիզմը» [41]։
Իրավիճակը սրեց «ընտրության աքսիոմի» հայտնաբերումը (1904 թ., Զերմելո), որը, պարզվում է, անգիտակցաբար կիրառվել է մաթեմատիկական բազմաթիվ ապացույցներում (օրինակ՝ իրական թվերի տեսության մեջ)։
XX դարի սկզբին հնարավոր եղավ պայմանավորվել բազմությունների տեսության մի տարբերակի շուրջ՝ զերծ նախկինում հայտնաբերված հակասություններից (դասի տեսություն), այնպես որ մաթեմատիկոսների մեծ մասն ընդունեց բազմությունների տեսությունը։ века удалось сՍակայն մաթեմատիկայի նախկին միասնությունն արդեն չկար, որոշ գիտական դպրոցներ մաթեմատիկայի հիմնավորման վերաբերյալ սկսեցին մշակել այլընտրանքային տեսակետներ[42]։
XX դար[խմբագրել | խմբագրել կոդը]
XX դարում մաթեմատիկոս մասնագիտության հեղինակությունը նկատելիորեն բարձրացավ։ Մաթեմատիկան զարգանում էր էքսպոնենցիալ Ստորև բերված են որոշ աառավել լուրջ ձեռքբերումները։
Նոր ուղղություններ[խմբագրել | խմբագրել կոդը]
XX դարում մաթեմատիկայի պատկերը զգալիորեն փոխվեց[43]։
- Էապես ընդլայնվեց ինչպես ինքնին մաթեմատիկան, այնպես էլ դրա կիրառման շրջանակը։Նոր բաժիններ ի հայտ եկան, բաժինների մեջ անսպասելի կապեր բացահայտվեցին (օրինակ, թվերի տեսության և հավանականությունների տեսության միջև[44])։
- Ի հայտ եկան նոր ընդհանրացնող հասկացություններ, մաթեմատիկան բարձրացավ աբստրակցիայի ավելի բարձր մակարդակի, որտեղից ավելի պարզ էր դառնում մաթեմատիկայի որպես գիտության միասնականությունը։ Դրանում առանձնահատուկ դեր խաղաց մաթեմատիկայի բոլոր բաժինների հիմունքների փոխակերպումը բազմությունների տեսության հիմքի վրա։ Երկրաչափությունը արդեն դիտարկում էր ամենաաբստրակտ տարածությունները, հանրահաշիվը թվային մաթեմատիկայից վերացականացավ և ամենանսովոր հատկություններով գործողություններ թույլատրեց։
- Կատարվեց մաթեմատիկայի հիմունքների և մաթեմատիկական տրամաբանության հնարավորությունների խորը վերլուծություն կապված մաթեմատիկական պնդումների ապացույցների հետ։

1900 թվականին, Մաթեմատիկոսների երկրորդ միջազգային կոնգրեսում, Դավիթ Հիլբերտը ներկայացրեց 23 չլուծված մաթեմատիկական խնդիրների ցուցակ։ Այս խնդիրներն ընդգրկում էին մաթեմատիկայի բազմաթիվ ոլորտներ և ձևավորեցին 20-րդ դարի մաթեմատիկոսների ջանքերի կիզակետը։ Ներկայումս այդ խնդիրներից տասը լուծված են, յոթը մասնակի են լուծված, երկուսը դեռևս բաց են։ Մնացած չորսը շատ ընդհանուր են ձևակերպված, ուստի անիմաստ է դրանց լուծման մասին խոսել։
20-րդ դարում առանձնահատուկ զարգացում ստացան մաթեմատիկայի նոր ոլորտները. Դա մեծապես պայմանավորված էր կառավարման տեսության, քվանտային ֆիզիկայի և այլ կիրառական առարկաների կարիքներով։
- Տոպոլոգիա.
- Ֆունկցիոնալ անալիզ.
- Դիսկրետ մաթեմատիկայի զանազան բաժիններ, այդ թվում՝ խաղերի տեսություն, գրաֆների տեսություն, կոդավորման տեսություն.
- Ինֆորմատիկա և Կիբեռնետիկա, Ինֆորմացիայի տեսություն, ալգորիթմների տեսություն.
- Լի խմբեր.
- Համակարգչային մոդելավորում։
- օպտիմիզացիայի տեսություն
- պատահական պրոցեսների տեսություն
- Մաթեմատիկական վիճակագրության մեթոդներ
Մաթեմատիկայի շատ հին ոլորտներ նույնպես արագ զարգացան։
- Հանրահաշվական երկրաչափություն
- Կոմպլեքս անալիզ, հատկապես շատ փոփոխականի ֆունկցիաների համար
- Մաթեմատիկական ֆիզիկա
- Ընդհանուր հանրահաշիվ
- Ռիմանի երկրաչափություն
- Հավանականությունների տեսություն
Մաթեմատիկական տրամաբանությունը և մաթեմատիկայի հիմքերը[խմբագրել | խմբագրել կոդը]
1931 թվականին Կուրտ Գոդելը հրապարակեց իր ոչ լրիվտության թեորեմներից երկուսը, որոնք հաստատեցին մաթեմատիկական տրամաբանության սահմանափակումները։ Սա վերջ դրեց Դավիթ Հիլբերտի ծրագրին` ստեղծել մաթեմատիկայի հիմունքների ամբողջական և ոչ հակասական համակարգ։ Մի փոքր ավելի վաղ՝ 1915-1920 թվականներին Լևենհայմի և Սքոլեմի ուսումնասիրություններում (Լևենհայմ-Սկոլեմի թեորեմ) մեկ այլ հուսահատեցնող փաստ բացահայտվեց. ոչ մի աքսիոմատիկ համակարգ չի կարող լինել կատեգորիկ։ Այլ կերպ ասած, անկախ նրանից, թե որքան ուշադիր ձևակերպված է աքսիոմների համակարգը, միշտ կլինի մի մեկնաբանություն, որը բացարձակապես նման չի նրան, որի համար այս համակարգը ստեղծվել է։ Այս հանգամանքը սասանում է նաև աքսիոմատիկ մոտեցման համընդհանուր լինելու հավատը։
Այնուամենայնիվ, հիմնարար սկզբունքները, պարզաբանելու համար ֆորմալ աքսիոմատիկան ճանաչվել է անհրաժեշտ։ Բացի այդ, աքսիոմատիզացիան օգնում է բացահայտել մաթեմատիկայի տարբեր ճյուղերի միջև ոչ ակնհայտ կապերը և դրանով իսկ նպաստում դրանց միավորմանը[45]։
Հիմնական արդյունքները ստացվել են ալգորիթմների տեսության մեջ։ Ցույց է տրվել, որ թեորեմը կարող է լինել ճիշտ, բայց ալգորիթմորեն անլուծելի (ավելի ճիշտ՝ հնարավոր չէ կառուցել ալգորիթմ, Չերչ, 1936)։
1933 թվականին Անդրեյ Կոլմոգորովը ավարտեց (այժմ համըընդհանուր ճանաչված) հավանականությունների տեսության աքսիոմատիկան։
1963 թվականին Փոլ Կոենը ապացուցեց, որ Կանտորի կոնտինիուումի վարկածն ապացուցելի չէ (բազմությունների տեսության սովորական աքսիոմատիկայում)։
Հանրահաշիվ և թվերի տեսություն[խմբագրել | խմբագրել կոդը]
Դարասկզբին Էմմի Նյոթերը և Վան դեր Վարդենը ավարտեցին ընդհանուր հանրահաշվի հիմունքների կառուցումը որի կառուցվածքային բաղադրիչները (խմբեր, դաշտեր, օղակներ, գծային տարածություններ և այլն) այժմ ներթափանցել են ողջ մաթեմատիկան։ Շուտով խմբերի տեսությունը մեծ հաջողությամբ ներթափանցեց ֆիզիկա և բյուրեղագրություն։

1910-ական թվականներին Ռամանուջանը ձևակերպեց ավելի քան 3000 թեորեմ, ներառյալ թվի բաժանման ֆունկցիայի հատկությունները և դրա ասիմպտոտիկ գնահատումները։ Նա նաև կարևոր արդյունքներ ստացավ գամմա ֆունկցիայի, մոդուլային ձևերի, դիվերգենտ շարքերի, հիպերերկրաչափական շարքերի և պարզ թվերի տեսության ուսումնասիրության մեջ։
1995 թվականին Էնդրյու Ուայլսն ապացուցեց Ֆերմայի վերջին թեորեմը՝ փակելով դարավոր խնդիրը։
Մաթեմատիկական անալիզ և մաթեմատիկական ֆիզիկա[խմբագրել | խմբագրել կոդը]
В начале XX դարի սկզբին Լեբեգը և Բորելը ընդհանրացրին Ժորդանի չափման տեսությունը. որի հիման վրա կառուցվեց Լեբեգի ինտեգրալը։ Հիլբերտի դպրոցում հայտնվեց ֆունկցիոնալ անալիզը, որը շուտով ուղղակի կիրառություն գտավ քվանտային ֆիզիկայում։

1960-ականներին Աբրահամ Ռոբինսոնը հրապարակեց ոչ ստանդարտ անալիզի նկարագրությունը՝ մաթեմատիկական անալիզի հիմնավորման այլընտրանքային մոտեցում, իրական անվերջ փոքրերի հիման վրա։
Ինտենսիվորեն զարգանում է բազմաչափ բազմաձևությունների տեսությունը՝ խթանվելով ֆիզիկայի կարիքներով։
Երկրաչափություն և տոպոլոգիա[խմբագրել | խմբագրել կոդը]
Ընդհանուր տոպոլոգիան սրընթաց զարգանում էր և կիրառություն գտնում մաթեմատիկայի տարբեր ճյուղերում։ Բենուա Մանդելբրոտի (1975) հայտնաբերած ֆրակտալները մասսայական հետաքրքրություն առաջացրին։ (1975)։
1907 թվականին Հերման Մինկովսկին մշակեց հարաբերականության հատուկ տեսության կինեմատիկայի երկրաչափական մոդելը, որը հետագայում Հարաբերականության ընդհանուր տեսության (ՀՀ) համար հիմք հանդիսացավ։ Այս երկու տեսություններն էլ հարթ բազմազանությունների բազմաչափ դիֆերենցիալ երկրաչափության արագ զարգացման խթան հանդիսացան, մասնավորապես՝Ռիմանյան և կեղծ Ռիմանյան։
Դիսկրետ և համակարգչային մաթեմատիկա[խմբագրել | խմբագրել կոդը]
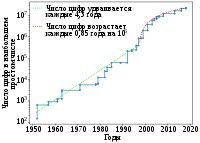
XX դարի վերջում, համակարգիչների ի հայտ գալու հետ կապված, մաթեմատիկական ջանքերի զգալի վերակողմնորոշում տեղի ունեցավ։ Զգալիորեն բարձրացավ այնպիսի բաժինների դերը, ինչպիսիք են թվային մեթոդները, օպտիմիզացիայի տեսությունը, շատ մեծ տվյալների բազաների հետ հաղորդակցությունը, արհեստական ինտելեկտը, աուդիո և վիդեո տվյալների կոդավորումը և այլն։ Նոր գիտություններ ի հայտ եկան՝ կիբեռնետիկա, ինֆորմատիկա, պատկերների ճանաչում, տեսական ծչագչավորում, ավտոմատ թարգմանության տեսություն, համակարգչային մոդելավորում, աուդիո և վիդեո ինֆորմացիայի կոմպակտ կոդավորում և այլն։
Մի շարք հին խնդիրներ լուծվել են համակարգչային ապացույցների միջոցով[46]. Վոլֆգանգ Հաքենը և Քենեթ Ափելը լուծեցին չորս գույների խնդիրը՝ օգտագործելով համակարգիչ (1976 թ.):
XXI դար[խմբագրել | խմբագրել կոդը]

2000 թվականին Կլեյի մաթեմատիկական ինստիտուտը կազմեց մաթեմատիկական յոթ կարևորագույն խնդիրների ցանկը «կարևոր դասական խնդիրներ, որոնց լուծումները երկար տարիներ է ինչ չեն գտնվել»։ 2003 թվականին հազարամյակի խնդիրներից մեկը՝ Պուանկարեի վարկածը, լուծեց Գրիգորի Պերելմանը։
21-րդ դարում մաթեմատիկական ամսագրերի մեծ մասն ունի առցանց տարբերակներ, իսկ որոշ ամսագրեր տպագրվում են միայն ինտերնետում։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ (Boyer 1991, "Euclid of Alexandria" p. 119)
- ↑ Клайн М. Математика. Утрата определённости, 1984, էջ 44—47
- ↑ Wigner E. P. The Unreasonable Effectiveness of Mathematics in the Natural Sciences // Communications on Pure and Applied Mathematics. — 1960. — № 13. — С. 1—14. Архивировано из первоисточника 28 փետրվարի 2011. См. русский перевод в книге Этюды о симметрии. — М.: Мир, 1971. или в УФН за март 1968 Արխիվացված 2012-03-23 Wayback Machine.
- ↑ Молодший В. Н. Очерки по вопросам обоснования математики. — М.: Учпедгиз, 1958. — С. 7.
- ↑ «Естественнонаучные познания древней Руси (XI–XV ВВ.)». www.portal-slovo.ru. Արխիվացված օրիգինալից 2020 թ․ սեպտեմբերի 24-ին. Վերցված է 2019 թ․ մայիսի 19-ին.
- ↑ Софья Ковалевская: первая в мире женщина – профессор математики // www.rosimperija.info. Архивировано из первоисточника 18 Մայիսի 2019.
- ↑ Неморарий. О данных числах / Пер. и прим. С. Н. Шрейдера. Под ред. И. Н. Веселовского // Историко-математические исследования. — 1959. — Т. XII. — С. 559—678.
- ↑ Зубов В. П. Из истории средневековой атомистики // Труды Института истории естествознания. — 1947. — Т. I. — С. 293.
- ↑ Орем Н. Трактат о конфигурации качеств // Историко-математические исследования / Пер. В. П. Зубова. —М., 1958. — В. 11. — С. 601—732.
- ↑ Александров А. Д. Математика, её содержание, методы и значение (в трёх томах). — АН СССР, 1956. — Т. 1. — С. 39—40. — 296 с.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. — М.: Наука, 1982. — (Библ. «Квант», вып. 14).
- ↑ История математики, 1970—1972, Том I, с. 304-305
- ↑ Fr. Viete. Introduction a l’art analytique. Bollettino di bibliografia e storia delle scienze matematiche e phisiche, v. I, 1868.
- ↑ Декарт Р. Геометрия Արխիվացված 2007-11-13 Wayback Machine // Рассуждение о методе, с приложениями / Пер., статьи и комментарии Г. Г. Слюсарева и А. П. Юшкевича. М.— Л.: Изд. Академии наук СССР, 1953.
- ↑ История математики, 1970—1972, Том II, с. 21
- ↑ Юшкевич А. П. Декарт и математика. // Р. Декарт. Геометрия. М.— Л.: 1938. С. 255—294.
- ↑ Декарт Р. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Пер., примечания и статья А. П. Юшкевича. М.— Л.: 1938.
- ↑ Бернулли Я. О законе больших чисел / Пер. Я. В. Успенского. Предисловие А. А. Маркова. М.: Наука, 1986.
- ↑ И. Кеплер. Новая стереометрия винных бочек Արխիվացված 2013-02-08 Wayback Machine / Пер. и предисловие Г. Н. Свешникова. Вступительная статья М. Я. Выгодского. М.— Л.: ГТТИ, 1935. С. 109.
- ↑ Кавальери Б. Геометрия, изложенная новым способом при помощи неделимых непрерывного, с приложением «Опыта IV» о применении неделимых к алгебраическим степеням / Пер., вступительная статья и комментарии С. Я. Лурье. М.— Л.: 1940.
- ↑ Ферма П. Введение в изучение плоских и пространственных мест. О максимуме и минимуме. Выдержки из переписки с Декартом // Р. Декарт. Геометрия. М.—Л.: 1938. С. 137—196.
- ↑ И. Ньютон. Математические работы / Пер., статьи и комментарии Д. Д. Мордухай-Болтовского. М.—Л.: 1937.
- ↑ Лейбниц Г. В. Избранные отрывки из математических сочинений / Составил и перевёл А. П. Юшкевич. — Успехи матем. наук, 1948. Т. III. В. I (23). С. 165—204.
- ↑ Антуан Арно. Новые начала геометрии (ֆր.՝ Nouveaux elements de geometrie), Париж, 1667.
- ↑ Ж. Лагранж. Аналитическая механика, т. I, II Արխիվացված 2008-08-01 Wayback Machine / Пер. В. С. Гохмана, под ред. Л. Г. Лойцянского и А. И. Лурье. М.—Л.: 1950.
- ↑ Лаплас П. С. Изложение системы мира. — Л.: Наука, 1982. 376 с.
- ↑ Л. Эйлер. Введение в анализ бесконечных. Т. I Արխիվացված 2013-05-01 Wayback Machine / Пер. Е. Л. Пацановского, статья А. Шпайзера, ред. И. Б. Погребысского. С. 109.
- ↑ Котек В. В. Леонард Эйлер. М.: Учпедгиз, 1961
- ↑ Лаплас П. Опыт философии теории вероятностей / Пер. A. I. B.; ред. А. К. Власова. М.: 1908.
- ↑ Панов В. Ф. Математика древняя и юная. — Изд. 2-е, исправленное. — М.: МГТУ им. Баумана, 2006. — С. 477. — 648 с. — ISBN 5-7038-2890-2
- ↑ Г. Монж. Начертательная геометрия / Пер. В. Ф. Газе, под редакцией Д. И. Каргипа. М.: 1947.
- ↑ Гаусс К. Ф. Общие исследования о кривых поверхностях Արխիվացված 2014-03-05 Wayback Machine // Основания геометрии. М.: ГИТТЛ, 1956.
- ↑ Стройк Д. Очерк истории дифференциальной геометрии. М.; Л.: Гостехиздат, 1941.
- ↑ Риман Б. Сочинения Արխիվացված 2013-05-01 Wayback Machine М.—Л.: ОГИЗ. ГИТТЛ, 1948.
- ↑ О. Л. Коши. Алгебраический анализ / Пер. Ф. Эвальда, В. Григорьева, А. Ильина. Лейпциг: 1864. С. VI.
- ↑ Гаусс К. Ф. Труды по теории чисел Արխիվացված 2011-09-14 Wayback Machine / Пер. Б. Б. Демьянова, общая ред. И. М. Виноградова, комментарии Б. Н. Делоне. М.: Изд-во АН СССР, 1959.
- ↑ Касселс Дж. Введение в геометрию чисел М.: Мир, 1965.
- ↑ Галуа Э. Сочинения. М.—Л.: ОНТИ, 1936.
- ↑ Проблемы Гильберта Արխիվացված 2013-06-01 Wayback Machine / Под ред. П. С. Александрова. М.: «Наука», 1969. С. 34.
- ↑ Джевонс С. Основы науки. СПб.: 1881.
- ↑ Клайн М. Математика. Утрата определённости, 1984, էջ 228—250
- ↑ Клайн М. Математика. Утрата определённости, 1984, էջ 251—299
- ↑ Александров А. Д. Математика, её содержание, методы и значение (в трёх томах). — АН СССР, 1956. — Т. 1. — С. 59—60. — 296 с.
- ↑ Постников А. Г. Вероятностная теория чисел. — М.: Знание, 1974. — 64 с. — (Новое в жизни, науке).
- ↑ Вейль Г. Полвека математики, 1969, էջ 7-8
- ↑ Грэхем, Рональд. Математика и компьютеры: проблемы и перспективы // Квант. — 2016. — № 3. — С. 2—9.
| ||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||
Քաղվածելու սխալ՝ <ref> tags exist for a group named "C", but no corresponding <references group="C"/> tag was found







