Տարրական հանրահաշիվ
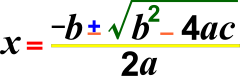
Տարրական հանրահաշիվ, հանրահաշվի հնագույն բաժինը, որն ուսումնասիրում է հանրահաշվական արտահայտություններ և հավասարումներ իրական թվերով։
Հիմնական հասկացություններ[խմբագրել | խմբագրել կոդը]
Հանրահաշվում ընդունված է գրել մաթեմատիկական արտահայտություններ (բանաձևեր) առավել ընդհանուր ձևով, կոնկրետ թվերը փոխարինելով այբբենական տառերի, որի շնորհիվ նմանատիպ խնդիրներ լուծելու համար օգտագործվում են այդ բանաձևերը։ Հանրահաշվի հիմնական պարունակությունը կայանում է կանոնների օգնությամբ բանաձևերի ինքնուրույն ձևափոխությունը, որոնցով անհրաժեշտ է լուծել հավասարումներ, վերլուծել կախվածությունը, օպտիմազացնել ոսումնասիրվող համակարգը և ուրիշ այլ գործնական խնդիրներ[1]։

Բացի տառերից և թվերից, տարրական հանրահաշվի բանաձևերում օգտագործվում են թվաբանական գործողություններ։
Երկու բանաձևերը, միացած իրար հետ հավասարության նշանով, անվանում են հավասարումներ։
Եթե երկու ֆորմուլաների միջև որևէ նշան չի դրված, ապա ընդունվում է որպես բազմապատկում.
Բանաձևի օրինակ. եռանկյան մակերեսը S ներկայացվում է որպես կողմերից մեկով a և a-ին տարված h բարձրությունով.
Ամենապարզ հանրահաշվական արտահայտությունը - դա միանդամն է, բաղկացած թվերից, որոնք բազմապատկված են մեկ կամ ավելի այբբենական տառերին[2].
Միանդամների հանրահաշվական գումարը կոչվում է բազմանդամ։ Արտահայտությունը, որը ունի ձև մի բազմանդամի բաժանումը մյուս բազմանդամին, կոչվում է հանրահաշվական կոտորակ։
Տարրական հանրահաշվի կանոնները[խմբագրել | խմբագրել կոդը]
Արտահայտության արժեքի հաշվումը[խմբագրել | խմբագրել կոդը]
Գործողությունների կատարման հերթականությունը նշվում է փակագծերով։
- Թվի աստիճան բարձրացնելը
- Ֆունկցիայի արժեքի հաշվում
- Բազմապատկում և բաժանում
- Գումարում և հանում
Օրինակ.
Արտահայտության արժեքը հաշվելիս այբբենական տառերի փոխարեն տեղադրում են թվային արտահայտությունները, համապատասխան խնդիրներին։ Բազմաթիվ լուծումների բազմությունը, որոնց տեղադրելու դեպքում արտահայտությունը իմաստ ունի կոչվում է Թույլատրելի Արժեքների Բազմություն ( կրճատ ՝ ԹԱԲ )[3]։
Օրինակ ՝ արտահայտության համար Թույլատրելի Արժեքների Բազմությունը ՝ բոլոր a և b թվերը որոնց դեպքում ։
Գործողությունների հատկությունները[խմբագրել | խմբագրել կոդը]
Գումարելիների տեղափոխությունից գումարը չի փոխվում.
Հանումը գումարումի հակառակ գործողությունն է.
Արտադրիչների տեղափոխությունից արտադրյալը չի փոխվում.
Բաժանումը բազմապատկման հակառակ գործողությունն է։ 0 - ի վրա բաժանում անհնար է։ b - ի վրա բաժանում նույն է, ինչ որ բազմապատկում b - ի հակադարձ թվի վրա.
Թվի աստիճան բարձրացնելը կոմմուտատիվ չէ։ Դրա համար էլ կան երկու հակառակ գործողություններ ՝ թվի աստիճան բարձրացնելը և թվի արմատ հաշվելը։
Ասոցիատիվ հատկությունը գումարման․ Ասոցիատիվ հատկությունը բազմապատկման․
Դիստրիբուտիվ հատկությունը բազմապատկման․
Դիստրիբուտիվ հատկությունը աստիճան բարձրացնելու․
Գումարումը աստիճանի ցուցիչի․
Բազմապատկումը աստիճանի ցուցիչի․
Հավասարումների հատկություններ[խմբագրել | խմբագրել կոդը]
- Եթե a = b և b = c, ուրեմն a = c ( հավասարման տրանզիտիվություն )
- a = a ( ռեֆլեքսություն )
- Եթե a = b, ուրեմն b = a ( սիմմետրիկություն )
Ուրիշ կանոններ[խմբագրել | խմբագրել կոդը]
- Եթե a = b և c = d, ուրեմն a + c = b + d։
- Եթե a = b, ուրեմն a + c = b + c
- Եթե a = b և c = d, ուրեմն ac = bd։
- Եթե a = b, ուրեմն ac = bc
- Եթե a > b և b > c, ուրեմն a > c
- Եթե a > b, ուրեմն a + c > b + c
- Եթե a > b և c > 0, ուրեմն ac > bc
- Եթե a > b և c < 0, ուրեմն ac < bc
Որոշ հանրահաշվական ինքնություններ[խմբագրել | խմբագրել կոդը]
Հավասարման լուծումը[խմբագրել | խմբագրել կոդը]
Հավասարումը - հավասարության տեսակ է․
Հավասարման լուծում - խնդիր է, պետք է գտնել լուծումների այնպիսի բազմություն, որոնց տեղադրելու դեպքում հավասարությունը ճիշտ է։ Լուծումների վրա կարող են դրված լինել հավելյալ պայմաններ։ Հավասարման լուծումը - մեկն է հանրահաշվի գլխավոր խնդիրներից և ընդհանրապես մաթեմատիկայի, պատմական գիտության զարգացման ժամանակահատվածում մշակվել են բազմաթիվ մեթեդներ կամ ալգորիթմներ հավասարումը լուծելու համար։
Պատմական ակնարկ[խմբագրել | խմբագրել կոդը]
Շատ վաղուց է ամրապնդվել հիմնական հատկություններով թվերով և մոտավոր ալգորիթմներով գրելու խորհրդանշական լեզուն։ Ի սկզբանե տառերը խորհրդանիշներ էին որոնցով հավասարման մեջ նշանակված էր անհայտը, որը պետք էր գտնել, ինչպես նաև այլ պայմանների դեպքում գտնել ստույգ թվային արժեքները։ Այն գաղափարը, որ հայտնի գործակիցները օգտակար են ընդհանուր արժեքի համար դժվարությամբ էր ներմուծվում։
Հանրահաշվական համակարգի մասին առաջին դատողությունները պահպանվել են Դիոֆմանտի «Արիֆմետիկա» գրքում։ Համարյա կասկած չկա, որ նա կարող էր օգտվել իր նախորդներից, քանի որ հայտնի չեն ոչ այդպիսի մարդիկ, ոչ էլ նման աշխատություններ, ինչպիսի հնարավորություն ունեին օրինակ Արքիմեդը, Էվկլիդեսը և ուրիշներ։ Անգամ մինչև XV դարը նա հետևորդներ չուներ։ Եվրոպայում Արֆիմետիկայի թարգմանությանը ծանոթացել են միայն XVI դարում, և նրա մեթոդները մեծ նշանակություն ունեցան Ֆերմի և Վիետի վրա։
Թվաբանության հիմնական պրոբլեմը – ռացիոնալ գործակիցներով անորոշ հավասարումների ռացիոնալ լուծումները գտնելն է։ Դիոֆանտի մոտ օգտագործվում է այբբենական սիմվոլներ։ Թվաբանության մեջ Դիոֆանտը օգտագործում է հետևյալ նշանակումները. Անհայտը նա անվանում է թիվ և նշանակում է ξ տառով։ Ամեն-ինչ նա արտահայտում է անհայտով։ Շատ կաննոներ են մեզ հայտնի. Նշանի փոխում հավասարման ուրիշ մաս տեղափոխելով, ընդհանուր անդամներ կրճատելով և ուրիշ։
Միջին դարերում հնդիկ մաթեմատիկները թեթևակիորեն առնչվել են այս թեմաներին, նրանց սիմվոլիկան ավելի հարուստ էր, սակայն ավելի խրթին։
Եվրոպայում լույս տեսած գրքերում ինչպիսիք են Ջորդան Նեմորարի XIII դար «Թվաբանությունը» և «Թվերի տվյալները»,դեռևս տարանջատված չէին հանրահաշիվը և երկրաչափությունը։ Նա ինչպես նաև Ֆիբոնաչին նմանեցնում էին արտահայտությունների հայեցակարգերը, սակայն դեռևս նրանք միացված չէին։ XV դարի հայտնի մաթեմատիկոս Լուկա Պաչոլին ներկայացնում է իր տեսությունը հանրահաշվական սիմվոլիկայի մասին, որը այնքան էլ տարածված և դյուրին չէր։
16-րդ դարի վերջին հանրահաշվական լեզվի մասին իր արմատական բարեփոխումները ներկայացրեց Ֆրանսուա Վիետը, ով մասնագիտությամբ իրավաբան էր, սակայն հոգու խորքում մատեմատիկոս։ Նա հստակ ներկայացրեց վերջնական նպատակը և զարգացման նոր փուլ մտցրեց ընդհանուր թվաբանության տեսությունը։ Վիետը օգտագործեց թվային գործակիցներ տերմինը։ Հաշվի առնելով թվային օրինակները խնդիրները կարելի է լուծել ընդհանուր ձևով։ Վիետը ազատորեն կիրառել է հանրահաշվական բարեփոխումները, փոփոխականների փոփոխությունը և հանրահաշվական տեխնիկան։
Վիետի համակարգը առաջացնում էր համընդհանուր հիացմունք։ Նա հնարավորինս լավ է նկարագրել թվաբանական օրենքների և ալգորիթմների նախկինում ունեցած աներևակայելի ընդհանրության կապերը։ Սակայն Վիետի սիմվոլիկան համահունչ չէր ժամանակին, որը և դժվարություն էր առաջացնում։ Եվ ահա գիտնականներ տարբեր երկրներից սկսեցին բարելավվել այն։ Անգլիացի Թոմաս Հերրիոտը իր գրքում, որը լույս էր տեսել նրա մահից հետո 1831 թվականին շատ ավելի մոտ էր ժամանակակից սիմվոլիկային, որը նշանակում է որ արդեն փոփոխված էին մեծատառ և փոքրատառերը, օգտագործում էր հավասարման նշանը և իր հորինած համեմատության ‘’ <’’ և ‘’ >’’ նշանները։
Հանրահաշվական սիմվոլիկային ժամանակակից տեսք է տվել Ռենե Դիկարտը 17-րդ դարում։ Այս գործընթացի արդյունքը և եզրակացությունը դարձավ Նյուտոնի «Ընդհանուր թվաբանություն» աշխատությունը։ Մնացած մի քանի մանրամասներին ուղղում տվեց Էյլերը։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Элементарная математика, 1976, էջ 70.
- ↑ Элементарная математика, 1976, էջ 73.
- ↑ Элементарная математика, 1976, էջ 71.
| ||||||||||||||||||||||||||||||||||||||||||||||
























