Կատեգորիաների տեսություն

Կատեգորիաների տեսություն, արդի մաթեմատիկայի վերացական բաժիններից. մաթեմատիկական օբյեկտներն ուսումնասիրում է դրանց կառուցվածքի հետ համաձայնեցված արտապատկերումների հետ։ Շնորհիվ իր համահյուսող և միասնականացնող դերի կատեգորիաների տեսությունը բազմությունների տեսության հետ կազմում է արդի մաթեմատիկայի հիմքը։

Կատեգորիաների տեսության ուսումնասիրության առարկան, ընդհանուր առմամբ, կատեգորիաներն ու ֆունկտորներն են։ Կատեգորիայի հասկացությունը կազմվում է երեք մասից.

1. կատեգորիայի օբյեկտների համախմբություն,
2. յուրաքանչյուր $A,B$ օբյեկտների համար տրված $Mor(A,B)$ մորֆիզմների բազմություն (որի տարրերը նշանակվում են $\varphi :A\to B$),
3. մորֆիզմների արտադրյալ կամ համադրություն, որը մորֆիզմների յուրաքանչյուր $\varphi :A\to B$ և $\psi :B\to C$ զույգին համապատասխանեցնում է $\psi _{0}\varphi :A\to C$ մորֆիզմ։

Կատեգորիայի մորֆիզմները և դրանց արտադրյալը պետք է բավարարեն հետևյալ պայմաններին.
ա. ցանկացած $\varphi :A\to B,\psi :B\to C,\chi :C\to D$ մորֆիզմների եռյակի համար՝ $\chi \cdot (\psi \cdot \varphi )=(\chi \cdot \psi )\cdot \varphi$ (արտադրյալի զուգորդականություն),
բ. կամայական $A$ օբյեկտի համար գոյություն ունի այնպիսի $1_{A}:A\to A$ մորֆիզմ, որ ինչպիսիք էլ լինեն $\varphi :A\to B$ և $\psi :C\to A$ մորֆիզմները՝ $\varphi \cdot 1_{A}=\varphi$ և $1_{A}\cdot \psi =\psi$ (միավոր մորֆիզմի գոյություն),
գ. $Mor(A,B)$ և $Mor(C,D)$ բազմությունները չունեն ընդհանուր տարր, եթե $A\neq C$ կամ $B\neq D$։

Կատեգորիաների երկու տարրական օրինակ.

1. օբյեկտներ համարենք հարթության բոլոր եռանկյունների բազմությունը, կամայական $A,B$ եռանկյունների համար $Mor(A,B)$՝ $A$-ն $B$-ին տանող բոլոր հոմոտետիաների բազմությունը, իսկ մորֆիզմների համադրություն՝ հոմոտետիաների արտադրյալը։
2. Օբյեկտներ համարենք հարթության բոլոր շրջանագծերը, $Mor(a,b)$-ն՝ $a$ շրջանագիծը $b$ շրջանագծին տանող հոմոտետիաների բազմությունը, իսկ մորֆիզմների համադրություն՝ հոմոտետիաների արտադրյալը (այս օրինակներում $Mor(A,B)$ և $Mor(C,D)$ բազմությունների հավասար հոմոտետիաները համարվում են տարբեր մորֆիզմներ, եթե $A\neq C$ կամ $B\neq D$։

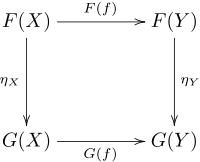
Դիցուք ունենք երկու կատեգորիա՝ Ա և Բ։ Ասում են, որ տրված է $\Phi$ կովարիանտ (կոնտրավարիանտ) ֆունկտոր Ա-ից Բ, եթե Ա-ի յուրաքանչյուր $A$ օբյեկտին համապատասխանեցված է Բ-ի որոշակի $\Phi (A)$ օբյեկտ և Ա-ի յուրաքանչյուր $\varphi :A\to B$ մորֆիզմին՝ Բ-ի $\Phi (\varphi ):\Phi (A)\to \Phi (B)$ [համապատասխանաբար $\Phi (\varphi ):\Phi (B)\to \Phi (A)$] մորֆիզմը, ընդ որում բավարարվում են հետևյալ պայմանները,
ա. մորֆիզմների համադրության պատկերը համընկնում է մորֆիզմների պատկերների համադրության հետ, այսինքն՝ ցանկացած $\varphi :A\to B$ և $\psi :B\to C$ մորֆիզմների համար $\Phi (\psi _{0}\varphi )=\Phi (\psi _{0})\Phi (\varphi )$ [համապատասխանաբար $\Phi (\varphi _{0}\psi )=\Phi (\varphi _{0})\Phi (\psi )$],
բ. յուրաքանչյուր միավոր մորֆիզմի պատկերը միավոր մորֆիզմ է՝ $\Phi (1_{A})=1_{\Phi (A)}$։ Օրինակ, եռանկյանը համապատասխանեցնելով նրան ներգծված շրջանագիծ, իսկ եռանկյունների հոմոտետիային՝ ներգծյալ շրջանագծերի համապատասխան հոմոտետիան, կստանանք ֆունկտոր վերը նշված օրինակների առաջին կատեգորիայից երկրորդի մեջ։

Կատեգորիաների տեսության դերն ու նշանակությունը մաթեմատիկայում որոշվում է նրանով, որ այնպիսի հիմնական մաթեմատիկական հասկացություններ, ինչպիսիք են բազմությունները և նրանց արտապատկերումները, խմբերը և նրանց հոմոմորֆիզմները, տոպոլոգիական տարածություններն ու նրանց հոմոմորֆիզմները են, կազմում են կատեգորիա, ընդ որում կատեգորիաների տեսությունը հնարավորություն է տալիս մասնավոր տիպի կատեգորիաներն ուսումնասիրող գիտությունների սահմաններում ծագած հասկացություններին նայել նոր, ավելի ընդհանուր տեսանկյունից։ Կատեգորիա հասկացությունը սահմանել են Էյլենբերգն ու Մակլեյնը (1945)։ Կատեգորիաների տեսության զարգացումը 50-ական թվականներին գլխավոր առմամբ կապված էր հոմոլոգիաների տեսության և հանրահաշվական տոպոլոգիայի բուռն զարգացման հետ։ Ներկայումս կատեգորիաների տեսությունը մաթեմատիկայի արագ զարգացող ճյուղերից է և հետզհետե վերածվում է ինքնուրույն գիտության։

Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից  (հ․ 5, էջ 288)։