Ֆոտոն
Ֆոտոն (հին հունարեն՝ φῶς` «լույս»), տարրական մասնիկ, էլեկտրամագնիսական ճառագայթման (նեղ իմաստով՝ լույսի) քվանտ։ Ֆոտոնը չունի հանգստի զանգված և կարող է գոյություն ունենալ միայն լույսի արագությամբ շարժվելիս։ Ֆոտոնի էլեկտրական լիցքը նույնպես զրո է։ Ֆոտոնը կարող է գտնվել միայն երկու սպինային վիճակներում՝ շարժման ուղղության վրա ±1 սպինի պրոյեկցիայով (պարույրությամբ)։ Դասական էլեկտրադինամիկայում այս հատկությանը համապատասխանում է էլեկտրամագնիսական ալիքների շրջանային աջ և ձախ բևեռացումը։ Որպես քվանտային մասնիկ՝ ֆոտոնին ներհատուկ է մասնիկ-ալիքային երկվությունը, այսինքն՝ ֆոտոնը ունի և մասնիկին, և դը Բրոյլի ալիքին բնորոշ հատկանիշներ։
Հանգստի զանգվածի զրոյական լինելու փաստը հաշվի առնելով՝ մի շարք հեղինակներ ֆոտոնը համարում են քվազիմասնիկ[7][8]։
Քվազիմասնիկների նման, ֆոտոնն ունի զրոյական հանգստի զանգված, սակայն տարածման համար միջավայրի կարիք չունի, ինչպես մյուս տարրական մասնիկները։
Ֆոտոնը նշանակվում է տառով, այդ պատճառով հաճախ այն անվանում են գամմա-քվանտ (հատկապես բարձր էներգիայով ֆոտոնները)։ Ստանդարտ մոդելի տեսանկյունից ֆոտոնը տրամաչափային բոզոն է։ Վիրտուալ ֆոտոնները[9] էլեկտրամագնիսական ճառագայթումը կրողներն են, ուստի ապահովում են փոխազդեցություն, օրինակ, երկու էլեկտրական լիցքերի միջև[10]։ Ֆոտոնը Տիեզերքում ամենաշատ տարածված մասնիկն է։ Մեկ նուկլոնին ընկնում է շուրջ 20 միլիարդ ֆոտոն[11]։
Պատմություն[խմբագրել | խմբագրել կոդը]
Լույսի ժամանակակից տեսությունը հիմնված է բազմաթիվ գիտնականների աշխատանքի վրա։ Էլեկտրամագնիսական դաշտի ճառագայթման և կլանման քվանտային բնույթը 1900 թ. առաջին անգամ ձևակերպել է Մաքս Պլանկը` ջերմային ճառագայթումը բացատրելու համար։ «Ֆոտոն» տերմինի հեղինակը քիմիկոս Հիլբերտ Լյուիսն է (1926 թ.)[12]: 1905-1917 թթ. Այնշտայնը հրապարակեց գիտափորձերի և Մաքսվելի դասական հավասարումների միջև եղած հակասությունների մասին վկայող մի շարք աշխատանքներ[13][14][15][16], մասնավորապես, ֆոտոէֆեկտի և էլեկտրամագնիսական ճառագայթման հետ ջերմային հավասարակշռության մեջ գտնվող նյութի հատկության մասին։ Փորձեր արվեցին լույսի քվանտային հատկությունը բացատրել կիսադասական մոդելներով, որոնցում լույսը նախկինի պես նկարագրվում էր Մաքսվելի հավասարումներով` առանց հաշվի առնելու քվանտացումը, իսկ լույս առաքող և կլանող մարմիններին վերագրվում էին քվանտային հատկություններ (տե՛ս օրինակ Բորի տեսությունը)։ Չնայած կիսադասական մոդելները իրենց ազդեցությունը թողեցին քվանտային մեխանիկայի զարգացման վրա (ինչի մասին մասնավորապես վկայում է այն, որ որոշ դրույթներ և նույնիսկ հետևություններ բացահայտորեն ընդգրկված են ժամանակակից քվանտային տեսության մեջ)[17], փորձերը հաստատեցին Այնշտայնի ճշմարտացիությունը լույսի քվանտային բնույթի մասին (տե՛ս օրինակ ֆոտոէֆեկտ)։ Պետք է նշել, որ էլեկտրամագնիսական ճառագայթման էներգիայի քվանտացումը բացառություն չէ։ Քվանտային տեսության մեջ բազմաթիվ ֆիզիկական մեծությունների արժեքներ դիսկրետ (քվանտացված) են։ Օրինակ` անկյունային մոմենտը, սպինը, կապված համակարգերի էներգիան։ Ֆոտոնի հասկացության կիրառումը նպաստեց նոր տեսությունների և ֆիզիկական սարքերի ստեղծմանը և խթանեց քվանտային մեխանիկայի փորձարարական և տեսական բազայի զարգացումը։ Օրինակ, հայտնագործվեցին լազերը, մազերը, բացահայտվեց Բոզե-Այնշտայնի կոնդենսացման երևույթը, ձևակերպվեցին դաշտի քվանտային տեսությունը և քվանտային մեխանիկայի հավանակային մեկնաբանությունը։ Տարրական մասնիկների ֆիզիկայի ժամանակակից ստանդարտ մոդելում ֆոտոնի գոյությունը հետևանք է այն բանի, որ տարածություն-ժամանակի ցանկացած կետում ֆիզիկական օրենքները ինվարիանտ են լոկալ տրամաչափային համաչափության նկատմամբ։ Այդ համաչափությամբ են որոշվում ֆոտոնի ներքին հատկությունները, ինչպես օրինակ էլեկտրական լիցքը, զանգվածը, սպինը։ Ֆոտոնի հասկացության կիրառումներից են ֆոտոքիմիան[18], վիդեոտեխնիկան, համակարգչային տոմոգրաֆիան, մեծ թույլատվությամբ միկրոսկոպիան և միջմոլեկուլային հեռավորությունների չափումը։ Ֆոտոնը կիրառվում է նաև որպես քվանտային համակարգչի և տվյալների փոխանցման համար նախատեսված գիտական սարքերի տարր (տե՛ս քվանտային կրիպտոգրաֆիա)։
Անվանումների և նշանակումների պատմությունը[խմբագրել | խմբագրել կոդը]
Սկզբնապես Ալբերտ Այնշտայնը ֆոտոնը կոչեց «Լուսային քվանտ» (գերմ.՝ das Lichtquant)[13]: Ներկայիս անվանումը ֆոտոնը ստացել է քիմիկոս Հիլբերտ Լյուիսի կողմից 1926 թ.[19], որն իր հրապարակած տեսության մեջ ֆոտոնն անվանում է «անստեղծելի և անոչնչացնելի»[20]։ Չնայած Լյուիսի տեսությունը փորձարարական տվյալներին հակասելու պատճառով տարածում չգտավ, բազմաթիվ ֆիզիկոսներ սկսեցին օգտագործել էլեկտրամագնիսական դաշտի քվանտի նոր անվանումը։ Հունարեն ֆոտոն նշանակում է «լույս»։ Ֆիզիկայում ֆոտոնը սովորաբար նշանակվում է հունական այբուբենի «գամմա» տառով՝ : Այս նշանակումը առաջ է եկել 1900 թ. հայտնաբերված գամմա-ճառագայթումից, որը կազմված է բավականին մեծ էներգիա ունեցող ֆոտոններից։ Գամմա-ճառագայթումը՝ իոնացնող ճառագայթման երեք տեսակներից (ալֆա-մասնիկներ, բետա-տրոհում և գամմա-ճառագայթներ) մեկը, հայտնաբերել է Պաուլ Ուլրիխ Վիլլարդը, իսկ դրանց էլեկտրամագնիսական բնույթը 1914 թ. ապացուցել են Էռնեստ Ռեզերֆորդը և Էդուարդ Անդրեյդը։ Քիմիայում և օպտիկական ինժեներիայում ֆոտոնների համար հաճախ կիրառվում է նշանակումը, որտեղ -ը Պլանկի հաստատունն է, -ն ` ֆոտոնի հաճախությունը։
Ֆոտոնի հասկացության զարգացման պատմությունը[խմբագրել | խմբագրել կոդը]

18-րդ դարում մշակված տեսությունների մեծ մասում լույսը դիտարկվում էր որպես մասնիկների հոսք։ Նման տեսություններից մեկը 1021 թ. շարադրել է Իբն ալ Հայսամը իր «Օպտիկայի մասին գրքում», որտեղ գիտնականը լուսային ճառագայթը ներկայացնում է որպես փոքրագույն մասնիկների հոսք։ Այս մասնիկները «չունեն ոչ մի հայտնի հատկություն, բացի էներգիայից»[21]։ Քանի որ նման մոդելները չկարողացան բացատրել այնպիսի երևույթներ, ինչպիսիք են բեկումը, դիֆրակցիան և կրկնակի բեկումը, առաջարկվեց լույսի ալիքային տեսությունը, որի հիմնադիրները դարձան Ռենե Դեկարտը (1963 թ. )[22], Ռոբերտ Հուկը (1665)[23], և Քրիստիան Հյուգենսը (1678 թ.)[24]: Սակայն գերիշխողը լույսի դիսկրետ կազմության վրա հիմնված մոդելներն էին՝ գլխավորապես Իսահակ Նյուտոնի հեղինակության ազդեցության շնորհիվ[25][26]։ XIX դարի սկզբում Թոմաս Յունգը և Օգյուստեն Ֆրենելը իրենց փորձերում ակնառու կերպով ցույց տվեցին լույսի ինտերֆերենցի և դիֆրակցիայի երևույթներ, ինչից հետո մոտ 1850 թ. ալիքային մոդելները սկսեցին լայն ընդունելություն գտնել[27] 1856 թ. Ջեյմս Մաքսվելը իր տեսության[28] շրջանակներում առաջարկեց, որ լույսը էլեկտրամագնիսական ալիք է։ 1888 թ. Հենրիխ Հերցը փորձնականորեն հաստատեց այս հիպոթեզը՝ առաջին անգամ նկատելով ռադիոալիքները [29]:
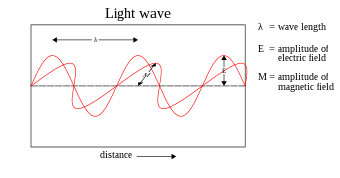
Մաքսվելի ալիքային տեսությունը, սակայն, ի զորու չէ բացատրել լույսի բոլոր հատկությունները։ Այդ տեսության համաձայն, լուսային ալիքի էներգիան պետք է կախված լինի միայն լույսի ինտենսիվությունից, բայց ոչ հաճախությունից։ Իրականում որոշ փորձերի արդյունքներ հակառակը ցույց տվեցին. լույսից ատոմներին հաղորդված էներգիան կախված է միայն լույսի հաճախությունից, այլ ոչ ինտենսիվությունից։ Օրինակ, որոշ քիմիական ռեակցիաներ կարող են սկսվել միայն նյութը այնպիսի լույսով լուսավորելիս, որի հաճախությունը գերազանցում է որոշակի շեմային արժեքը, իսկ այդ արժեքից փոքր հաճախություն ունեցող ճառագայթները, անկախ ինտենսիվությունից, չեն կարող որևէ ռեակցիա հարուցել։ Համանմանորեն, մետաղե թաղանթից էլեկտրոններ կարելի է պոկել միայն այնպիսի լույսով լուսավորելիս, որն ունի որոշակի սահմանից բարձր հաճախություն։ Այդ սահմանը կոչվում է ֆոտոէֆեկտի կարմիր սահման։ Բացարձակ սև մարմնի ճառագայթման հատկությունների հետազոտությունները, որոնք տևեցին գրեթե քառասուն տարի[30], ավարտվեցին Պլանկի հիպոթեզով[31][32]։ Ըստ դրա՝ հաճախությամբ էլեկտրամագնիսական ճառագայթում կլանելիս կամ ճառագայթելիս ցանկացած համակարգի էներգիան փոփոխվում է միայն էներգիայի քվանտին համեմատական մեծությունով, այսինքն՝ ընդհատաբար (դիսկրետ), -ը Պլանկի հաստատունն է։ Ալբերտ Այնշտայնը ցույց տվեց, որ քվանտացման մասին նման պատկերացումը պետք է ընդունել նաև նյութի և էլեկտրամագնիսական ճառագայթման միջև դիտվող ջերմային հավասարակշռությունը բացատրելու համար։ Դրա հիման վրա նա տեսականորեն բացատրեց ֆոտոէլեկտրական երևույթը, ինչի համար 1921 թ. ստացավ ֆիզիկայի Նոբելյան մրցանակը[33]։ Ի հակառակ դրա, Մաքսվելի տեսությունը համարում է, որ էլեկտրամագնիսական ճառագայթումը կարող է ունենալ կամայական էներգիա (այսինքն՝ էներգիան չի քվանտացվում)։ Սկզբնապես բազմաթիվ ֆիզիկոսներ ենթադրում էին, որ էներգիայի քվանտացումը էլեկտրամագնիսական ալիքները կլանող և ճառագայթող նյութի ինչ-որ անհայտ հատկության արդյունքն է։ 1905 թ. Այնշտայնը ենթադրեց, որ էներգիայի քվանտացումը հենց էլեկտրամագնիսական ճառագայթման հատկությունն է[13]։ Բացարձակ սև մարմնի ճառագայթման օրենքից ելնելով՝ Այնշտյանը ցույց տվեց, որ էներգիայի քվանտը պետք է նաև ունենա իմպուլս։ Ֆոտոնի իմպուլսը նկատվեց փորձնական եղանակով[34]։ Իր փորձի համար Արթուր Կոմպտոնը 1927 թ. արժանացավ Նոբելյան մրցանակի ֆիզիկայից։ Մաքսվելի տեսությունը փորձարարական նոր արդյուքների հետ համաձայնեցնելու բազմաթիվ ջանքեր գործադրվեցին։ Ներկայումս ֆիզիկայում Պլանկի գաղափարը և դրա հիման վրա մշակված Այնշտայնի հիպոթեզը էլեկտրամագնիսական ճառագայթման քվանտային բնույթի մասին համարվում են ապացուցված։
Ֆոտոնի ֆիզիկական հատկությունները[խմբագրել | խմբագրել կոդը]

Ֆոտոնը զանգված և լիցք չունեցող մասնիկ է։ Ֆոտոնի սպինը 1 է, սակայն հանգստի զրոյական զանգված ունենալու հետևանքով ավելի հարմար է այս մասնիկը նկարագրել պարույրությամբ՝ մասնիկի սպինի պրոյեկցիայով շարժման ուղղության վրա։ Ֆոտոնը կարող է գտնվել միայն երկու սպինային վիճակներում, որոնց պարույրությունը է։ Դասական էլեկտրադինամիկայում այս հատկությանը համապատասխանում է էլեկտրամագնիսական ալիքի լայնականությունը։ Ֆոտոնի արագությունը հավասար է լույսի արագությանը։ Ուստի, քանի որ գոյություն չունեն այնպիսի հաշվարկման համակարգեր, որոնցում ֆոտոնը գտնվում է դադարի վիճակում, մասնիկի ներքին զույգությունը հայտնաբերված չէ։ արտահայտությունից ֆոտոնին կարելի է վերագրել ռելյատիվիստական զանգված։ Ֆոտոնը չեզոք մասնիկ է, նույնական է իր հակամասնիկին[35], այդ պատճառով նրա լիցքային զույգությունը բացասական է և հավասար է -1։ Ֆոտոնը բոզոն է, մասնակցում է էլեկտրամագնիսական և ձգողական փոխազդեցություններին։ Ինչպես նշվեց, չունի էլեկտրական լիցք, բացի այդ, վակուումում չի տրոհվում՝ կայուն (ստաբիլ) է։ Ֆոտոնը կարող է գտնվել բևեռացման երկու վիճակներից որևէ մեկում և նկարագրվել երեք տարածական պարամետրերով՝ ալիքային վեկտորի բաղադրիչներով, ինչով որոշվում է նրա ալիքի երկարությունը և տարածման ուղղությունը։ Բնական բազմաթիվ պրոցեսներում ֆոտոն է ճառագայթվում։ Օրինակ, արագացումով շարժվող էլեկտրական լիցքի դեպքում, ատոմի կամ միջուկի՝ գրգռված վիճակից ավելի փոքր էներգիայով վիճակի անցնելու դեպքում կամ էլեկտրոն-պոզիտրոն զույգի անիհիլացիայի ժամանակ[36]։ Եթե ֆոտոնի էներգիան հավասար է , ապա իմպուլսը էներգիայի հետ կապված է առնչությամբ, որտեղ -ն լույսի արագությունն է (ֆոտոնի շարժման արագությունը)։ Համեմատության համար նշենք, որ հարաբերականության հատուկ տեսության համաձայն, ոչ զրոյական հանգստի զանգված ունեցող մասնիկի համար զանգվածի և իմպուլսի կապը էներգիայի հետ որոշվում է բանաձևով։ Վակուումում ֆոտոնի էներգիան և իմպուլսը կախված են միայն նրա հաճախությունից (կամ, որ նույնն է, ալիքի երկարությունից).
- ,
- :
Հետևաբար, իմպուլսի մեծությունը՝
- ,
որտեղ-ը Պլանկի հաստատունն է՝ , -ը՝ ալիքային վեկտորը, -ն՝ ալիքային թիվը, -ը՝ անկյունային հաճախությունը։ ալիքային վեկտորը ցույց է տալիս ֆոտոնի շարժման ուղղությունը։ Ֆոտոնի սպինը կախված չէ հաճախությունից։
Մասնիկ-ալիքային երկվությունը և անորոշությունների սկզբունքը[խմբագրել | խմբագրել կոդը]
Ֆոտոնին ներհատուկ է մասնիկ-ալիքային երկվությունը։ Ֆոտոնը էլեկտրամագնիսական ալիքի հատկություններ է դրսևորում դիֆրակցիայի և ինտերֆերենցի երևույթներում՝ այն դեպքում, երբ արգելքների բնութագրական չափերը համեմատական են ֆոտոնի ալիքի երկարությանը։ Օրինակ, կրկնակի ճեղքով անցնող, , հաճախություն ունեցող միայնակ ֆոտոնների հաջորդականությունը էկրանին ստեղծում է ինտերֆերենցային պատկեր, որը կարելի է նկարագրել Մաքսվելի հավասարումներով[37]։ Դրանով հանդերձ, փորձերը ցույց են տալիս, որ ֆոտոնները ամբողջությամբ ճառագայթվում կամ կլանվում են այնպիսի օբյեկտների կողմից, որոնց չափերը շատ անգամ փոքր են ֆոտոնի ալիքի երկարությունից (օրինակ՝ ատոմները) կամ էլ որոշ մոտավորությամբ կարող են նույնիսկ համարվել կետային օբյեկտներ (օրինակ՝ էլեկտրոնները)։ Այսպիսով, ճառագայթման և կլանման պրոցեսներում ֆոտոններն իրենց դրսևորում են որպես կետանման մասնիկներ։ Սակայն այս նկարագրությունը բավարար չէ. ֆոտոնի պատկերացումը որպես կետային մասնիկ, որի հետագիծը հավանակային կերպով որոշում է էլեկտրամագնիսական դաշտը, ժխտվում է կոռելյացիոն փորձերով (տե՛ս նաև Այնշտայն-Պոդոլսկի-Ռոզենի պարադոքսը)։

Քվանտային մեխանիկայի հիմնարար սկզբունքներից է Հայզենբերգի անորոշությունների սկզբունքը, որը թույլ չի տալիս միաժամանակ որոշել մասնիկի տարածական կոորդինատը և իմպուլսը[38]։ Պետք է նշել, որ լիցքավորված, զանգված ունեցող մասնիկի համար անորոշությունների սկզբունքը պահանջում է, որ լույսը քվանտացվի։ Դա կարելի է բացատրել իդեալական միկրոսկոպով անցկացվող հայտնի մտային փորձի օգնությամբ՝ որոշելով էլեկտրոնի կոորդինատը նրա վրա լույս գցելու և ցրված լույսը գրանցելու միջոցով (Հայզենբերգի գամմա-միկրոսկոպ)։ Էլեկտրոնի դիրքը կարելի է որոշել ճշտությամբ, որը հավասար է միկրոսկոպի թույլտվությանը։ Ելնելով դասական օպտիկայի պատկերացումներից՝
որտեղ-ն միկրոսկոպի բացվածքն է։ Այսպիսով, կոորդինատի անորոշությունը ցանկության դեպքում կարելի է փոքրացնել՝փոքրացնելով ընկնող ճառագայթների ալիքի երկարությունը։ Սակայն ցրումից հետո էլեկտրոնը ձեռք է բերում որոշակի լրացուցիչ իմպուլս, որի անորոշությունը հավասար է : Եթե ընկնող ճառագայթումը քվանտացված չլիներ, այս անորոշությունը հնարավոր կլիներ անընդհատ փոքրացնել՝ փոքրացնելով ճառագայթման ինտենսիվությունը։ Ալիքի երկարությունը և ընկնող լույսի ինտենսիվությունը կարելի է փոփոխել միմյանցից անկախ։ Արդյունքում, լույսի քվանտացման բացակայության դեպքում, հնարավոր կլիներ մեծ ճշտությամբ միաժամանակ որոշել էլեկտրոնի դիրքը և իմպուլսը, ինչը հակասում է անորոշությունների սկզբունքին։
Հակառակը, Այնշտայնի բանաձևը ֆոտոնի իմպուլսի համար ամբողջությամբ բավարարում է անորոշությունների սկզբունքի պահանջներին։ Հաշվի առնելով, որ ֆոտոնը ցանկացած ուղղությամբ կարող է ցրվել անկյան սահմաններում, էլեկտրոնին հաղորդված իմպուլսի անորոշությունը հավասար է
- :
Առաջին արտահայտությունը բազմապատկելով երկրորդով՝ կստանանք Հայզենբերգի անորոշությունների սկզբունքը՝ : Այսպիսով, քվանտացված է ամբողջ աշխարհը. եթե նյութը ենթարկվում է քվանտային մեխանիկայի օրենքներին, ապա դաշտը նույնպես պետք է ենթարկվի այդ օրենքներին, և ընդհակառակը[39]։ Նման կերպով անորոշությունների սկզբունքը ֆոտոնների համար արգելում է էլեկտրամագնիսական ալիքի ֆոտոնների թվաքանակի և այդ ֆոտոնների փուլի միաժամանակյա չափումը.
- :
Ե՛վ ֆոտոնները, և՛ հանգստի զանգված ունեցող տարրական մասնիկները իրար մոտ տեղադրված երկու ճեղքերով անցնելիս տալիս են նման ինտերֆերենցային պատկերներ։ Ֆոտոնի համար այս երևույթը կարելի է նկարագրել Մաքսվելի հավասարումների օգնությամբ, մինչդեռ զանգված ունեցող մասնիկների համար օգտագործվում է Շրյոդինգերի բանաձևը։ Կարելի էր ենթադրել, որ Մաքսվելի հավասարումները Շրյոդինգերի հավասարման պարզեցված տարբերակն են ֆոտոնի համար։ Սակայն ֆիզիկոսների մեծ մասը համաձայն չէ դրա հետ[40][41]։ Մի կողմից, այդ հավասարումները մաթեմատիկորեն տարբերվում են միմյանցից. ի տարբերություն Մաքսվելի հավասարումների, որոնք նկարագրվում են կոորդինատային և ժամանակային իրական ֆունկցիաներով, Շրյոդինգերի հավասարումը կոմպլեքս է (դրա լուծումը հանդիսացող դաշտը ընդհանուր դեպքում կոմպլեքս ֆունկցիա է)։ Մյուս կողմից, ալիքային ֆունկցիայի հավանակային բնույթը, որը բացահայտորեն մտնում է Շրյոդինգերի հավասարման մեջ, չի կարող վերաբերվել ֆոտոնին[42]։ Քանի որ ֆոտոնը զանգված չունեցող մասնիկ է, չի կարող տեղայնացվել տարածության մեջ՝ առանց ոչնչանալու։ Ֆոտոնը չի կարող ունենալ կոորդինատային սեփական վիճակ, ուստի Հայզենբերգի անորոշությունների սկզբունքը տեսքով կիրառելի չէ նրա հանդեպ[43]։ Ֆոտոնի համար առաջարկվել են ալիքսյին ֆունկցիայի փոփոխված տարբերակներ[44][45][46][47], սակայն դրանք համընդհանուր տարածում չեն գտել։ Դրա փոխարեն ֆիզիկայում օգտագործվում է քվանտային էլեկտրադինամիկայի երկրորդային քվանտացման տեսությունը, որտեղ ֆոտոնները դիտարկվում են որպես էլեկտրամագնիսական մոդերի քվանտային գրգռումներ։
Ֆոտոնային գազի Բոզե-Այնշտայնի մոդելը[խմբագրել | խմբագրել կոդը]
Ամբողջ թվով սպին ունեցող մասնիկների համակարգի նկատմամբ կիրառվող քվանտային վիճակագրությունը լույսի քվանտների համար 1924 թ. առաջ է քաշել հնդիկ ֆիզիկոս Շատենդրանատ Բոզեն, զարգացրել է Ալբերտ Այնշտայնը բոզե-մասնիկների համար։ Որևէ ծավալում պարփակված էլեկտրամագնիսական ճառագայթումը կարելի է դիտարկել որպես գործնականում գրեթե չփոխազդող ֆոտոններից կազմված իդեալական գազ։ Այդ ֆոտոնային գազը թերմոդինամիկական հավասարակշռության է հասնում խոռոչի պատերի հետ փոխազդելու միջոցով։ Դա տեղի է ունենում այն ժամանակ, երբ պատերը ճառագայթում են այնքան ֆոտոն, որքան կլանում են։ Ընդ որում ծավալի ներսում հաստատվում է մասնիկների հավանականությունների որոշակի բաշխում ըստ էներգիայի։ Բացարձակ սև մարմնի ջերմային ճառագայթումը Բոզեն ստացել է առանց էլեկտրադինամիկայի օգնությանը դիմելու, պարզապես ձևափոխելով փուլային տարածության մեջ ֆոտոնների համակարգի քվանտային վիճակների հաշվարկը [48]: Մասնավորապես նա գտավ, որ այն ֆոտոնների թիվը, որոնց էներգիան պատկանում է -ից միջակայքին, բացարձակ սև խոռոչում հավասար է[49]
- ,
որտեղ-ն խոռոչի ծավալն է, -ը՝ Պլանկի հաստատունը, -ն՝ հավասարակշիռ ֆոտոնային գազի ջերմաստիճանը (հավասար է խոռոչի պատերի ջերմաստիճանին)։
Հավասարակշռության վիճակում բացարձակ սև խոռոչի էլեկտրամագնիսական ճառագայթումը նկարագրվում է նույն ջերմադինամիկական պարամետրերով, ինչ և սովորական գազը` ծավալ, ջերմաստիճան, էներգիա, էնտրոպիա և այլն։ Քանի որ ֆոտոններն օժտված են իմպուլսով, ճառագայթումը ճնշում է գործադրում անոթի պատերի վրա։ Ճնշման և ջերմաստիճանի կապն արտահայտվում է ֆոտոնային գազի վիճակի հավասարումով`
Որտեղ -ն Ստեֆան-Բոլցմանի հաստատունն է։ Այնշտայնը ցույց տվեց, որ այս ձևափոխությունը համարժեք է նրան, որ ֆոտոնները խստորեն նույնական են միմյանց, իսկ նրանց միջև կա «խորհրդավոր ոչ լոկալ փոխազդեցություն»[50][51], որը ներկայումս ընկալվում է որպես նույնական մասնիկների քվանտամեխանիկական վիճակների համաչափության պահանջ մասնիկների տեղափոխության նկատմամբ։ Այդ աշխատությունը բերեց կոհերենտ վիճակների հասկացությանը և նպաստեց լազերի հայտնագործմանը։ Այդ հոդվածներում Այնշտայնը ընդարձակեց Բոզեի պատկերացումները ամբողջ սպինով տարրական մասնիկների (բոզոնների) վերաբերյալ և կանխատեսեց այլասերված բոզոնային գազի մասնիկների զանգվածային անցումները նվազագույն էներգիայով վիճակի՝ ջերմաստիճանը մինչև որոշակի կրիտիկական սահման իջեցնելիս (Բոզե-Այնշտայնի կոնդենսացում)։ Այս երևույթը 1995 թ. դիտվեց փորձնականորեն, իսկ 2001 թ. փորձի հեղինակին շնորհվեց Նոբելյան մրցանակ[52]։ Ներկա պատկերացումների համաձայն, բոզոնները, այդ թվում և ֆոտոնները, ենթարկվում են Բոզե-Այնշտայնի վիճակագրությանը, իսկ ֆերմիոնները, օրինակ՝ էլեկտրոնները՝ Ֆերմի-Դիրակի վիճակագրությանը[53]։
Ինքնակամ և հարկադրական ճառագայթումներ[խմբագրել | խմբագրել կոդը]

1916 թ. Այնշտայնը ցույց տվեց, որ Պլանկի ճառագայթման օրենքը բացարձակ սև մարմնի համար հնարավոր է ստանալ՝ ելնելով հետևյալ վիճակագրական կիսադասական պատկերացումներից.
- Ատոմում էլեկտրոնները գտնվում են դիսկրետ (ընդհատ) էներգիական մակարդակներում։
- Էլեկտրոնների՝ մի մակարդակից մյուսը անցնելիս ատոմը ճառագայթում կամ կլանում է ֆոտոն։
Բացի այդ ենթադրվում էր, որ ատոմների կողմից լույսի ճառագայթումը կամ կլանումը տեղի են ունենում միմյանցից անկախ, և համակարգի ջերմային հավասարակշռությունը պահպանվում է ատոմների փոխազդեցության հաշվին։ Դիտարկենք ջերմային հավասարակշռության վիճակում գտնվող, էլեկտրամագնիսական ճառագայթումով լցված խոռոչ, որը կարող է առաքվել կամ կլանվել պատերի նյութի կողմից։ Ջերմային հավասարակշռության վիճակում ճառագայթման սպեկտրային խտությունը, որը կախված է ֆոտոնի հաճախությունից, միջինում չպետք է փոփոխվի ժամանակի ընթացքում։ Դա նշանակում է, որ ցանկացած հաճախությամբ ֆոտոն ճառագայթելու հավանականությունը պետք է հավասար լինի նրա կլանման հավանականությանը։ Այնշտայնը սկզբում ձևակերպեց պարզ առնչություններ ճառագայթման և կլանման ռեակցիաների արագությունների միջև։ Նրա մոդելում հաճախությամբ ֆոտոնների կլանման արագությունը և ատոմների անցումը էներգիական մակարդակից ավելի բարձր էներգիական մակարդակ ուղիղ համեմատական է էներգիայով ատոմների թվին և նույն հաճախությունն ունեցող շրջակա ֆոտոնների ճառագայթման սպեկտրային խտությանը՝
- :
Այստեղ -ն կլանման ռեակցիայի արագության հաստատունն է (կլանման գործակիցը)։ Հակադարձ պրոցեսի իրականացման համար երկու հնարավորություն կա՝ ֆոտոնների ինքնակամ ճառագայթումը և էլեկտրոնի վերադարձը ավելի ցածր էներգիական մակարդակ պատահական ֆոտոնի հետ փոխազդելու միջոցով։ Վերը նկարագրված մոտեցման համաձայն, ռեակցիայի համապատասխան արագությունը, որը բնութագրում է համակարգի կողմից հաճախությամբ ֆոտոնների ճառագայթումը և ատոմի անցումը բարձր էներգիական մակարդակից ցածր էներգիական մակարդակ, հավասար է՝
- :
Այստեղ -ն ինքնակամ (սպոնտան) ճառագայթման գործակիցն է, -ն՝ պատահական ֆոտոնների ազդեցությամբ հարկադրական ճառագայթման գործակիցը։ Ջերմադինամիկական հավասարակշռության վիճակում ատոմների թիվըև էներգիական վիճակներում միջինում պետք հաստատուն լինի ժամանակի ընթացքում, հետևաբար, և մեծությունները պետք է հավասար լինեն։ Բացի այդ, Բոլցմանի կինետիկական հավասարմանը համանմանորեն, պետք է տեղի ունենա
առնչությունը, որտեղ -ն և էներգիական վիճակների այլասերման բազմապատիկն է, -ն՝ այդ մակարդակների էներգիան, -ն՝ Բոլցմանի հաստատունը, -ն՝ համակարգի ջերմաստիճանը։ Ասվածից հետևում է, որ և
- .
-նև -ն կոչվում են Այնշտայնի գործակիցներ[54]։
Այնշտայնին չհաջողվեց ամբողջությամբ բացատրել այս հավասարումները, սակայն նա համարում էր, որ ապագայում հնարավոր կլինի հաշվել , գործակիցները, երբ «մեխանիկան և էլեկտրադինամիկան կփոխվեն այնպես, որ համապատասխանեն քվանտային հիպոթեզին»[55] Այնշտայնի կանխատեսումը իրականացավ 1926 թ., երբ Պոլ Դիրակը, կիրառելով կիսադասական մոտեցում, ստացավ հաստատունը[56], իսկ 1927 թ., ելնելով քվանտային տեսության հիմնական սկզբունքներից, հաջողությամբ գտավ բոլոր հաստատունները[57][58]։ Այդ աշխատությունը դարձավ քվանտային էլեկտրադինամիկայի, այսինքն՝ էլեկտրամագնիսական դաշտի քվանտացման տեսության հիմքը։ Դիրակի մոտեցումը, որը ստացավ երկրորդային քվանտացում անվանումը, դարձավ դաշտի քվանտային տեսության հիմնական եղանակներից մեկը[59][60][61]։ Եվս մեկ անգամ նշենք, որ վաղ քվանտային տեսության մեջ էլեկտրամագնիսական դաշտը չէր դիտարկվում որպես քվանտամեխանիկական, այլ՝ միայն նյութի մասնիկները։
Այնշտայնը չնկարագրեց ֆոտոնի ինքնակամ ճառագայթման ուղղությունը, ուստի մտահոգված էր իր տեսության անավարտվածության համար։ Լուսային մասնիկների շարժման հավանակային բնույթը առաջին անգամ դիտարկել էր Նյուտոնը կրկնակի բեկման երևույթը (լույսի ճառագայթի երկու բաղադրիչների բաժանվելու երևույթը անիզոտրոպ միջավայրերում) և, ընդհանրապես, երկու միջավայրերի բաժանման սահմանին լուսային փնջի՝ անդրադարձված և բեկված փնջերի բաժանվելու երևույթը, բացատրելիս։ Նյուտոնը ենթադրում էր, որ լուսային մասնիկները բնութագրող «թաքնված փոփոխականները» որոշում են, թե երկու ճառագայթներից որ մեկում կհայտնվի տվյալ մասնիկը[25]։ Այնշտայնը նույնպես, հեռանալով քվանտային մեխանիկայից, հույս ուներ, որ կստեղծվի միկրոաշխարհի ավելի ընդհանուր տեսություն, որտեղ պատահականությունը կյանք չի ունենա[62]։ Ուշագրավ է, որ ալիքային ֆունկցիայի հավանակային մեկնաբանությայն ներածության մեջ Մաքս Բոռնը[63][64] հենվում էր ավելի ընդհանուր տեսություն որոնող Այնշտայնի վերջին աշխատության վրա[65]
Երկրորդային քվանտացում[խմբագրել | խմբագրել կոդը]

1910 թ. Պետեր Դեբայը ստացավ Պլանկի բանաձևը` ելնելով համեմատաբար պարզ մի ենթադությունից[66]։ Բացարձակ սև խոռոչում գտնվող էլեկտրամագնիսական դաշտը նա վերլուծեց ըստ Ֆուրիեի մոդերի և ենթադրեց, որ յուրաքանչյուր մոդի էներգիան ամբողջ թվով բազմապատիկ է որտեղ -ն տվյալ մոդին համապատասխանող հաճախությունն է։ Ստացված մոդերի երկրաչափական գումարը իրենից ներկայացնում է Պլանկի ճառագայթման բանաձևը։ Սակայն, օգտագործելով այս մոտեցումը, հնարավոր չէ ճիշտ բանաձև ստանալ ջերմային ճառագայթման էներգիայի ֆլուկտուացիաների համար։ 1909 թ. Այնշտայնին հաջողվեց լուծել այս խնդիրը[14]։ 1925 թ. Մաքս Բոռնը, Վերներ Հայզենբերգը և Պասկուալ Յորդանը Դեբաևի մոտեցումը այլ կերպ մեկնաբանեցին[67]։ Կիրառելով դասական պատկերացումները, կարելի է ցույց տալ, որ էլեկտրամագնիսական դաշտի Ֆուրիեի շարքը էլեկտրամագնիսական հարթ ալիքների լրիվ հավաքածու է, որոնցից յուրաքանչյուրը համապատասխանում է իր ալիքային վեկտորին և բևեռացման վիճակին և համարժեք չէ չփոխազդող հարմոնիկ տատանակների համախմբությանը։ Քվանտային մեխանիկայի տեսակետից նման տատանակների էներգիական մակարդակները որոշվում են առնչությամբ, որտեղ -ն տատանակի հաճախությունն է։ Սկզբունքորեն նոր քայլ էր այն, որ էներգիայով մոդը այստեղ դիտարկվում է որպես ֆոտոնների վիճակ։ Այդ մոտեցումը թույլ տվեց ստանալ ճիշտ բանաձև բացարձակ սև մարմնի ճառագայթման էներգիայի ֆլուկտուացիաների համար։

Պոլ Դիրակը ավելի հեռուն գնաց[57][58]։ Փոխազդեցությունը լիցքի և էլեկտրամագնիսական դաշտի միջև նա դիտարկեց որպես ոչ մեծ գրգռում, որը ֆոտոնային վիճակներում անցումներ է հարուցում` փոփոխելով ֆոտոնների թիվը մոդերում և անփոփոխ թողնելով համակարգի լրիվ էներգիան և իմպուլսը։ Ելնելով դրանից, Դիրակը կարողացավ ստանալ և Այնշտայնի գործակիցները և ցույց տվեց, որ Բոզե-Այնշտայնի վիճակագրությունը ֆոտոնների համար էլեկտրամագնիսական դաշտի ճշգրիտ քվանտացման բնական հետևանքն է (Բոզեն դատում էր հակառակ ուղղությամբ. նա ստացավ Պլանկի ճառագայթման օրենքը բացարձակ սև մարմնի համար՝ ելնելով Բոզե-Այնշտայնի վիճակագրական բաշխումից)։ Այդ ժամանակ դեռ հայտնի չէր, որ բոլոր բոզոնները, ներառյալ ֆոտոնները, ենթակա են Բոզե-Այնշտայնի բաշխմանը։
Խոտորումների տեսությունը երկրորդ կարգի մոտավորությամբ դիտարկելիս Դիրակը ներմուծեց վիրտուալ ֆոտոնի հասկացությունը որպես էլեկտրամագնիսական դաշտի կարճատև միջանկյալ վիճակ։ Էլեկտրաստատիկև մագնիսական փոխազդեցությունները տեղի են ունենում այդ վիրտուալ ֆոտոններով փոխանակության արդյունքում։ Դաշտի քվանտային այդպիսի տեսությունում դիտարկվող պատահարների հավանականության լայնույթը հաշվարկվում է բոլոր հնարավոր, այդ թվում՝ ոչ ֆիզիկական միջանկյալ ճանապարհները գումարելու միջոցով. այսպես, պարտադիր չէ, որ վիրտուալ ֆոտոնը բավարարի դիսպերսիոն առնչությանը, որը տեղի ունի ֆիզիկական, զանգված չունեցող մասնիկների համար, և կարող է ունենալ լրացուցիչ բևեռացման վիճակ (իրական ֆոտոնն ունի երկու բևեռացում, սակայն վիրտուալ ֆոտոնը կարող է ունենալ երեք կամ չորս, կախված օգտագործվող վեկտորական պոտենցիալի չափումից)։ Չնայած վիրտուալ մասնիկները, մասնավորապես վիրտուալ ֆոտոնները չեն կարող անմիջականորեն դիտարկվել[68], դրանք չափելի ներդրում են ունենում դիտարկվող քվանտային պատահարների հավանականության մեջ։ Ավելին, խոտորումների տեսության երկրորդ և ավելի բարձր կարգի հաշվարկները երբեմն որոշ ֆիզիկական մեծությունների համար տալիս են անվերջ մեծ արժեքներ։ Այդ ոչ ֆիզիկական անսահմանությունները վերացնելու նպատակով դաշտի քվանտային տեսության մեջ մշակված է վերանորմավորման եղանակը[69]։ Գումարի մեջ կարող են ներդրում ունենալ այլ վիրտուալ մասնիկներ։ Օրինակ, երկու ֆոտոն անուղղակիորեն կարող են փոխազդել վիրտուալ էլեկտրոն-պոզիտրոնային զույգի միջոցով[70]։ Միջազգային գծային կոլայդերի աշխատանքի հիմքում դրվելու է այս մեխանիզմը[71]։
Մաթեմատիկորեն երկրորդային քվանտացման եղանակն այն է, որ մեծ թվով նույնական մասնիկներից բաղկացած քվանտային համակարգը նկարագրվում է ալիքային ֆունկցիաների օգնությամբ, որոնցում լրացման թվերը հանդես են գալիս որպես անկախ փոփոխականներ։ Երկրորդային քվանտացումն իրականացվում է՝ տրված վիճակում մասնիկների թիվը (լրացման թիվ) մեկով մեծացնող կամ փոքրացնող օպերատոր մտցնելու ճանապարհով։ Այս օպերատորները երբեմն կոչվում են ծնման և ոչնչացման օպերատորներ։ Լրացման և ոչնչացման օպերատորների մաթեմատիկական հատկությունները տրվում են փոխատեղման առնչություններով, որոնց տեսքը որոշվում է մասնիկների սպինով։ Նման նկարագրության դեպքում ալիքային ֆունկցիան նույնպես դառնում է օպերատոր։ Ժամանակակից ֆիզիկական նշանակումներում էլեկտրամագնիսական դաշտի քվանտային վիճակը գրվում է որպես Ֆոկի վիճակ, որը յուրաքանչյուր էլեկտրամագնիսական մոդի վիճակների թենզորական արտադրյալն է.
որտեղ -ը մոդում գտնվող թվով ֆոտոններով վիճակն է։ Նոր ֆոտոնի ստեղծումը (օրինակ՝ ատոմային անցման հետևանքով) գրվում է որպես.
- :
Ֆոտոնի կառուցվածքը[խմբագրել | խմբագրել կոդը]
Քվանտային քրոմադինամիկայի համաձայն՝ իրական ֆոտոնը կարող է փոխազդել ոչ միայն որպես առանձին կետային մասնիկ, այլև որպես քվարկների և գլյուոնների հավաքածու, ինչպիսին հադրոնն է։ Ֆոտոնի կառուցվածքը որոշվում է ոչ թե վալենտական քվարկների ավանդական հավաքածուներով (ինչպես, օրինակ, որոշվում է պրոտոնի կառուցվածքը), այլ՝ կետային ֆոտոնի վիրտուալ ֆլուկտուացիաներով պարտոնների հավաքածուում[72]։ Այս հատկություններն ի հայտ են գալիս միայն բավականաչափ մեծ էներգիաների դեպքում, սկսած ~1 ԳէՎ-ից։
Ֆոտոնը որպես տրամաչափային բոզոն[խմբագրել | խմբագրել կոդը]
Էլեկտրամագնիսական դաշտը նկարագրող Մաքսվելի հավասարումները կարող են ստացվել տրամաչափային տեսության պատկերացումներից՝ որպես տարածություն-ժամանակի կոորդինատի ձևափոխության նկատմամբ էլեկտրոնի տրամաչափային ինվարիանտության պահանջի կատարման հետևանք[73][74]։ Էլեկտրամագնիսական դաշտի համար այս տրամաչափային համաչափությունը արտացոլում է կոմպլեքս թվերի հատկությունը՝ կեղծ մասի փոփոխությունը առանց իրական մասի վրա ազդեցություն ունենալու, ինչպես էներգիայի կամ լագրանժյանի դեպքում է։ Նման տրամաչափային դաշտի քվանտը պետք է լինի առանց զանգվածի չլիցքավորված բոզոն, քանի դեռ չի խախտվել սիմետրիան։ Այդ պատճառով ֆոտոնը (որն էլ հենց հանդիսանում է էլեկտրամագնիսական դաշտի քվանտը) ժամանակակակից ֆիզիկայում դիտարկվում է որպես ամբողջ սպինով զանգված չունեցող չլիցքավորված մասնիկ։ էլեկտրամագնիսական փոխազդեցության կորպուսկուլային մոդելը ֆոտոնին վերագրում է 1-ի հավասար սպին, ինչը նշանակում է, որ ֆոտոնի պարույրությունը հավասար է : Դասական ֆիզիկայի տեսակետից ֆոտոնը կարող է մեկնաբանվել որպես մի պարամետր, որը պատասխանատու է լույսի բևեռացված վիճակի համար (շրջանային բևեռացված լուսային ալիքում լարվածության վեկտորի պտտման ուղղության համար)։ Քվանտային էլեկտրադինամիկայի շրջանակներում ներառված վիրտուալ ֆոտոնները կարող են գտնվել նաև ոչ ֆիզիկական բևեռացման վիճակներում[73]։
Ստանդարտ մոդելում ֆոտոնը էլեկտրաթույլ փոխազդեցություն իրականացնող չորս տրամաչափային բոզոններից մեկն է։ Մյուս երեքը (W+, W− և Z0) կոչվում են վեկտորական բոզոններ և պատասխանատու են միայն թույլ փոխազդեցության համար։ Ի տարբերություն ֆոտոնի, վեկտորային բոզոնը չի կարող չունենալ զանգված, քանի որ թույլ փոխազդեցությունն ի հայտ է գալիս միայն շատ փոքր հեռավորությունների վրա՝ <10−15 սմ։ Սակայն տրամաչափային դաշտերի քվանտները պետք է զանգված չունենան, զանգվածի ի հայտ գալը նրանց մոտ խախտում է շարժման հավասարումների տրամաչափային ինվարիանտությունը։ Այս դժվարությունից ելք առաջարկեց Պիտեր Հիգսը, ով տեսականորեն նկարագրեց էլեկտրաթույլ սիմետրիայի ինքնակամ խախտումը։ Այն թույլ է տալիս ծանր դարձնել վեկտորական բոզոնները՝ առանց խախտելու տրամաչափային համաչափությունը հենց շարժման հավասարումներում[74]։ Էլեկտրաթույլ փոխազդեցության մեջ ֆոտոնի միավորումը W և Z տրամաչափային բոզոնների հետ իրականացրեցին Շելդոն Լի Գլեշոուն, Աբդուս Սալամը և Սթիվեն Վայնբերգը, ինչի համար 1979 թ. արժանացան ֆիզիկայի Նոբելյան մրցանակի[75][76][77]։ Դաշտի քվանտային տեսության կարևոր խնդիրներից է նաև ուժեղ փոխազդեցության ընդգրկումը միասնական տրամաչափային սխեմայում (այսպես կոչված «Մեծ միավորման տեսությունը»)։ Սակայն այս տեսությունից բխող կարևորագույն հետևությունները, ինչպես, օրինակ, պրոտոնի տրոհումը, դեռ փորձարարական հաստատում չեն ստացել[78]։
Ֆոտոնի ներդրումը համակարգի զանգվածի մեջ[խմբագրել | խմբագրել կոդը]
հաճախությամբ ֆոտոն ճառագայթող համակարգի էներգիան փոքրանում է այդ ֆոտոնի էներգիային հավասար մեծությունով։ Արդյունքում համակարգի զանգվածը փոքրանում է չափով։ Համանմանորեն, ֆոտոն կլանող համակարգի զանգվածը համապատասխանաբար մեծանում է[79]։ Քվանտային էլեկտրադինամիկայում վակուումի վիրտուալ ֆոտոնների հետ էլեկտրոնների փոխազդեցության արդյունքում առաջ են գալիս տարամիտություններ, որոնք վերացվում են վերանորմավորման եղանակի օգնությամբ։ Արդյուքնում էլեկտրամագնիսական փոխազդեցության լագրանժյանում նստած էլեկտրոնի զանգվածը տարբերվում է փորձով դիտարկվող զանգվածից։ Անկախ որոշակի մաթեմատիկական դժվարություններից, որոնք կապված են նման գործողությունների հետ, քվանտային էլեկտրադինամիկան թույլ է տալիս շատ մեծ ճշտությամբ բացատրել այնպիսի փաստեր, ինչպիսիք են լեպտոնների անոմալ դիպոլային մոմենտը, և լեպտոնային դուպլետների գերնուրբ կառուցվածը (օրինակ, մյուոնիումների և պոզիտրոնիումների մոտ[80]։
Էլեկտրամագնիսական դաշտի էներգիա-իմպուլսի թենզորը տարբեր է զրոյից, այդ պատճառով ֆոտոնը ձգողական ազդեցություն է ունենում այլ օբյեկտների վրա՝ համաձայն հարաբերականության ընդհանուր տեսության։ Եվ ընդհակառակը, ֆոտոնը ենթարկվում է այլ օբյեկտների ձգողությանը։ Ձգողության բացակայության դեպքում ֆոտոնի հետագիծը ուղիղ գիծ է։ Ձգողական դաշտում այն շեղվում ուղիղ գծից՝ կապված տարածություն-ժամանակի կորացման հետ (տե՛ս օրինակ, ձգողական ոսպնյակ)։ Բացի այդ, ձգողական դաշտում դիտելի է այսպես կոչված ձգողական կարմիր սահմանը (տե՛ս Փաունդ-Ռեբկայի փորձը)։ Դա հատուկ է ոչ միայն առանձին ֆոտոնին։ Նման էֆեկտ կանխատեսվել է դասական էլեկտրամագնիսական ալիքի համար ամբողջությամբ[81]։
Ֆոտոնը նյութում[խմբագրել | խմբագրել կոդը]
Թափանցիկ միջավայրում լույսը ավելի փոքր արագությամբ է տարածվում, քան նրա [[|լույսի արագությունը վակուումում]] արագությունն է վակուումում։ Օրինակ, էներգիա ճառագայթող Արեգակի միջուկից դեպի մակերևույթ իրենց ճանապարհին ֆոտոնները ենթարկվում են բազմաթիվ բախումների, և մակերևույթին հասնելու համար կարող են միլիոնավոր տարիներ պահանջվել[82]։ Սակայն բաց տիեզերքում շարժվելիս նույն ֆոտոնները Երկիր են հասնում ընդամենը 8.3 րոպեում։ Լույսի արագության նվազումը բնորոշող մեծությունը կոչվում է նյութի բեկման ցուցիչ։ Դասական տեսանկյունից դանդաղեցումը կարելի է այսպես բացատրել։ Էլեկտրական դաշտի լարվածության ազդեցությամբ միջավայրի ատոմների վալենտական էլեկտրոնների լուսային ալիքները սկսում են հարկադրական հարմոնիկ տատանումներ կատարել։ Տատանվող էլեկտրոնները սկսում են որոշակի հապաղման ժամանակով երկրորդային ալիքներ ճառագայթել, որոնք ունեն նույն հաճախությունը և լարվածությունը, ինչ և ընկնող լույսը։ Ինտերֆերենցվելով սկզբնական ալիքի հետ՝ այդ ալիքները դանդաղեցնում են այն։ Կորպուսկուլային մոդելում հապաղումը կարելի է բացատրել նյութում քվանտային գրգռումներին (ֆոտոնի և էքսիտոնի նման քվազիմասնիկներ) ֆոտոնի միջամտությամբ, ինչի հետևանքով առաջանում է փոլարիտոն։ Նման փոլարիտոնն ունի զրոյից տարբեր էֆեկտիվ զանգված, ինչի հետևանքով արդեն չի կարող շարժվել արագությամբ։ Այլ քվազիմասնիկների հետ ֆոտոնի փոխազդեցության երևույթը կարելի է ուղղակիորեն դիտարկել Ռամանի և Բրիլյուենի ցրման երևույթներում[83]։
Նմանապես, ֆոտոնը կարելի է դիտարկել որպես միշտ, նույնիսկ նյութում, լույսի արագությամբ շարժվող մասնիկ, որը փուլային շեղման է ենթարկվում ատոմների հետ փոխազդեցության արդյունքում։ Ատոմները փոխում են ֆոտոնի ալիքի երկարությունը և իմպուլսը, բայց ոչ արագությունը[84] Կախված հաճախությունից՝ լույսը նյութում տարածվում է տարբեր արագություններով։ Այս երևույթը օպտիկայում կոչվում է դիսպերսիա։ Հատուկ պայմաններ ստեղծելով՝ կարելի է հասնել այն բանին, որ լույսի տարածման արագությունը նյութում դառնա շատ փոքր (այսպես կոչված «դանդաղ լույս»)։ Օգտագործելով էլեկտրամագնիսականորեն մակածված թափանցիկությունը՝ որոշակի հատուկ պայմաններում հնարավոր է հասնել մինչև 0,091 մմ/վ խմբային արագության[85]։
Ֆոտոնը կարող է նաև կլանվել միջուկների, ատոմների կամ մոլեկուլների կողմից՝ դրանով իսկ հարուցելով նրանց էներգիական վիճակների անցումներ։
Տեխնոլոգիական կիրառությունները[խմբագրել | խմբագրել կոդը]
Տեխնոլոգիայում ֆոտոնն ունի բազմաթիվ կիրառություններ։ Ստորև նկարագրված օրինակներն ընտրված են՝ ներկայացնելու համար ֆոտոնի կիրառությունը per se` ի տարբերություն հիմնական օպտիկական սարքերի, ինչպես օրինակ ոսպնյակը և այլն, որոնց գործողության սկզբունքը կարելի է բացատրել լույսի դասական տեսության շրջանակներում։ Ֆոտոնի կարևորագույն կիրառություններից մեկը լազերն է։ Առանձին Ֆոտոնի բազմաթիվ կիրառություններ կան։ Դասական ֆոտոէլեկտրոնային բազմապատկիչում գործարկվում է ֆոտոէֆեկտի երևույթը. մետաղյա թիթեղի վրա ընկնող ֆոտոնը էլեկտրոն է պոկում`սկզբնավորելով աստիճանաբար աճող էլեկտրոնային հոսք։ Կիսահաղորդիչներում նման երևույթ է կիրառվում լիցքային կապով սարքերում։ Այլ դետեկտորներում, ինչպիսին է Գեյգերի հաշվիչը, օգտագործվում են գազի մոլեկուլները իոնացնելու ֆոտոնի հատկությունը[86] Նյութի կողմից ֆոտոնի կլանումը և ճառագայթումը օգտագործվում է սպեկտրային անալիզում։ Ցանկացած քիմիական տարրի ատոմներ ունեն խստորեն որոշված ռեզոնանսային հաճախություններ, ինչի արդյունքում հենց այդ հաճախությունների վրա նրանք լույս են ճառագայթում կամ կլանում։ Դրա հետևանքով ատոմների և նրանցից կազմված մոլեկուլների ճառագայթման և կլանման սպեկտրները անհատական են, ինչպես մարդու մատնահետքերը։

Սպեկտրային անալիզի մի քանի եղանակներ կան.
- Ճառագայթային, որում օգտագործվում է ատոմների, հազվադեպ` մոլեկուլների ճառագայթման սպեկտրը։
- Կլանման, որում օգտագործվում է հիմնականում մոլեկուլների, բայց ոչ ատոմների, կլանման սպեկտրը։
- Ռենտգենյան, որում օգտագործվում են ատոմների ռենտգենյան սպեկտրները, ինչպես նաև ռենտգենյան ճառագայթների դիֆրակցիան հետազոտվող նյութում՝ վերջինիս կառուցվածքը բացահայտելու նպատակով։
Շատ պատահական թվերի գեներատորների աշխատանքի սկզբունքի հիմքում ընկած է միայնակ ֆոտոնի գտնվելու վայրի որոշումը։ Դրանցից մեկի գործողության պարզեցված սկզբունքը հետևյալն է. Պատահական հաջորդականության հերթական բիթը գեներացնելու համար ֆոտոնը ուղարկվում է լուսաբաժանի վրա։ Ցանկացած ֆոտոնի համար կա երկու հնարավորություն. կամ անցնել լուսաբաժանով կամ անդրադառնալ նրա նիստից։ Կախված արդյունքից՝ հաջորդականության հերթական բիթը գրվում է «0» կամ «1»[87][88]:
Վերջին հետազոտությունները[խմբագրել | խմբագրել կոդը]
Ներկայումս համարվում է, որ ֆոտոնի հատկությունները լավ հասկանալի են տեսության տեսանկյունից։ Ստանդարտ մոդելը դիտարկում է ֆոտոնը որպես որպես 1 սպինով, զրոյական հանգստի զանգվածով տրամաչափային բոզոն[89]։ և զրոյական էլեկտրական լիցքին։ Այս վերջին փաստը մասնավորապես հետևում է U(1) լոկալ ունիտար սիմետրիայից և էլեկտրամագնիսական փոխազդեցության վերաբերյալ փորձերից։ Սակայն ֆիզիկոսները շարունակում են փնտրել անհամապատասխանություններ փորձի և Ստանդարտ մոդելի դրույթների միջև։ Ֆոտոնի զանգվածի և լիցքի հայտնաբերմանը ուղղված փորձերի ճշտությունը մշտապես աճում են։ Ֆոտոնի՝ թեկուզ աննշան լիցք կամ զանգված ունենալը լուրջ հարված է Ստանդարտ մոդելին։ Մինչ այժմ անցկացված բոլոր փորձերը ցույց են տալիս, որ ֆոտոնը չունի ոչ լիցք[6], ոչ հանգստի զանգված[90][91][92][93][94][95][96][97][98][99][100][101]։ Ամենամեծ ճշտությունը, որով հաջողվել է չափել ֆոտոնի լիցքը, 5×10−52Կլ է (կամ 3×10-33 e)։ 1,1×10−52 կգ զանգվածի համար (6×10−17 էՎ/c2 կամ 1×10−22me)[102]: Ժամանակակից շատ հետազոտություններ ուղղված են ֆոտոնի կիրառմանը քվանտային օպտիկայի բնագավառում։ Ֆոտոնը հարմար մասնիկ է թվում գերարդյունաբերական քվանտային համակարգիչ ստեղծելու համար։ Քվանտային խճճվածության ուսումնասիրությունը նույնպես առաջատար է ժամանակակից հետազոտություններում[103]։ Բացի այդ, ուսումնասիրվում են ոչ գծային օպտիկական պրոցեսներն ու համակարգերը, մասնավորապես, երկֆոտոնային կլանման, համափուլ մոդուլյացիայի և օպտիկական պարամետրական օսցիլյատորների երևույթները։ Սակայն նման երևույթները և համակարգերը չեն պահանջում հատկապես ֆոտոնների կիրառում։ Դրանք հաճախ կարելի է մոդելավորել՝ ատոմը որպես ոչ գծային տատանակ դիտարկելու միջոցով։ Ինքնակամ պարամետրական ցրման ոչ գծային օպտիկական պրոցեսը հաճախ օգտագործվում է ֆոտոնների խճճված վիճակներ ստեղծելու համար[104]։ Վերջապես, ֆոտոններն օգտագործվում են օպտիկական հաղորդակցության, այդ թվում՝ նաև քվանտային գաղտնագրության մեջ[105]։
Տես նաև[խմբագրել | խմբագրել կոդը]
- Դոպլերի էֆեկտ
- Լույս
- Էլեկտրամագնիսական ճառագայթում
- Ֆոտոնիկա
- Էլեկտրամագնիսական ալիքների բևեռացում
- Լուսանկարչություն
- Լազեր
- Քվանտային օպտիկա
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Deutsche Nationalbibliothek Record #4045922-6 // Gemeinsame Normdatei (գերմ.) — 2012—2016.
- ↑ Gene Ontology release 2019-11-16 — 2019.
- ↑ 3,0 3,1 3,2 3,3 3,4 3,5 Gene Ontology release 2020-05-02 — 20200502 — 2020.
- ↑ 4,0 4,1 http://geneontology.org/external2go/rhea2go
- ↑ 5,0 5,1 Particle Data Group (2008)
- ↑ 6,0 6,1 Kobychev, V.V.; Popov, S.B. (2005). «Constraints on the photon charge from observations of extragalactic sources». Astronomy Letters. 31 (3): 147–151. arXiv:hep-ph/0411398. Bibcode:2005AstL...31..147K. doi:10.1134/1.1883345.(չաշխատող հղում) (անգլերեն) Altschul, B. (2007). «Bound on the Photon Charge from the Phase Coherence of Extragalactic Radiation». Physical Review Letters. 98: 261801. (անգլերեն)
- ↑ В. И. Перель. (2003). «Лекции Переля по Теории Твердого Тела». Научно-Образовательный Центр ФТИ им. А. Ф. Иоффе. Արխիվացված է օրիգինալից 2008 թ․ հոկտեմբերի 23-ին. Վերցված է 2012 թ․ փետրվարի 23-ին.
- ↑ Статья В. В. Мигулина «Электромагнитные волны», Большая советская энциклопедия, том 30, ст. 67-68, М.: Советская энциклопедия, 1978
- ↑ Д. В. Ширков, Виртуальные частицы, http://www.femto.com.ua/articles/part_1/0507.html, Гл. ред. Прохоров А. М., Физическая энциклопедия, М., Большая Российская энциклопедия, 1988, том 1
- ↑ «Электромагнитное взаимодействие». ФЭ. Արխիվացված է օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2009 թ․ հուլիսի 20-ին.
- ↑ Вайнберг С., Первые три минуты, [пер. с англ. В. Строкова] - М.: Эксмо, 2011. - 208 с. - ISBN 978-5-699-46169-1 п. Реликтовое излучение, с. 84
- ↑ Статья Э. А. Тагирова, Физический энциклопедический словарь, М.: Советская энциклопедия, 1984, ст. 826
- ↑ 13,0 13,1 13,2 Einstein А. (1905). «Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (trans. A Heuristic Model of the Creation and Transformation of Light)». Annalen der Physik. 17: 132–148.. An English translation is available from Wikisource.
- ↑ 14,0 14,1 Einstein А. (1909). «Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung (trans. The Development of Our Views on the Composition and Essence of Radiation)». Physikalische Zeitschrift. 10: 817–825.. An English translation is available from Wikisource.
- ↑ Einstein А. (1916). «Strahlungs-emission und -absorption nach der Quantentheorie». Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318.
- ↑ Einstein А. (1916). «Zur Quantentheorie der Strahlung». Mitteilungen der Physikalischen Geselschaft zu Zürich. 16: 47. Նաև Physikalische Zeitschrift, 18, 121-128 (1917)
- ↑ Редкин Ю. Н., Курс общей физики, Киров, ГГУ, 2006, ст. 152
- ↑ «Фотохимия». Кругосвет. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2009 թ․ ապրիլի 8-ին.
- ↑ Илья Леенсон. «Льюис, Гильберт Ньютон». Кругосвет. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2009 թ․ մարտի 13-ին.
- ↑ Lewis, G. N. (1926). «The conservation of photons». Nature. 118: 874–875. (անգլերեն)
- ↑ Rashed, R. (2007). «The Celestial Kinematics of Ibn al-Haytham». Arabic Sciences and Philosophy. Cambridge University Press. 17 (1): 7-55 [19]. doi:10.1017/S0957423907000355. «Իր օպտիկայում Հայթամը «լույսի փոքրագույն մասնիկները» բնութագրում է միայն այն հատկություններով, որոնք կարող են նկարագրվել երկրաչափորեն և ստուգվել փորձով» (անգլերեն)
- ↑ Descartes R. (1637). Discours de la méthode. Imprimerie de Ian Maire.
- ↑ Hooke R. (1667). Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon... London (UK): Royal Society of London.
- ↑ Huygens C. (1678). Traité de la lumière. . An English translation is available from Project Gutenberg
- ↑ 25,0 25,1 Newton I. (1952) [1730]. Opticks (4th ed.). Dover (NY): Dover Publications. Book II, Part III, Propositions XII-XX, Queries 25-29. ISBN 0-486-60205-2. (անգլերեն)
- ↑ «Свет». Кругосвет. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2009 թ․ մարտի 13-ին.
- ↑ Buchwald, J. Z. (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. University of Chicago Press. ISBN 0-226-07886-8. OCLC 18069573. (անգլերեն)
- ↑ Maxwell J. C. (1865). «A Dynamical Theory of the Electromagnetic Field». Philosophical Transactions of the Royal Society of London. 155: 459–512. doi:10.1098/rstl.1865.0008. (անգլերեն)
- ↑ Hertz H. (1888). «Über Strahlen elektrischer Kraft». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin). 1888: 1297–1307.
- ↑ Wien, W. (1911). «Wilhelm Wien Nobel Lecture». Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2012 թ․ փետրվարի 23-ին. (անգլերեն)
- ↑ Planck M. (1901). «Über das Gesetz der Energieverteilung im Normalspectrum». Annalen der Physik. 4: 553–563. doi:10.1002/andp.19013090310.
- ↑ Planck M. (1920). «Max Planck's Nobel Lecture». Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2012 թ․ փետրվարի 23-ին. (անգլերեն)
- ↑ «Текст речи Аррениуса для Нобелевской премии по физике 1921 года» (անգլերեն). The Nobel Foundation. 1922 թ․ դեկտեմբերի 10. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2009 թ․ մարտի 13-ին.
- ↑ Compton A, 1923, A Quantum Theory of the Scattering of X-rays by Light Elements, http://www.aip.org/history/gap/Compton/01_Compton.html Արխիվացված 2008-03-11 Wayback Machine>
- ↑ «Частицы элементарные». Кругосвет. Արխիվացված է օրիգինալից 2011 թ․ օգոստոսի 11-ին. Վերցված է 2009 թ․ մարտի 13-ին.
- ↑ Նշենք, որ անիհիլացիայի ժամանակ ճառագայթվում է ոչ թե մեկ, այլ` երկու ֆոտոն, քանի որ բախվող մասնիկների զանգվածների կենտրոնի համակարգում մասնիկների գումարային իմպուլսը հավասար է զրոյի, իսկ ճառագայթված մեկ ֆոտոնը միշտ կունենար ոչ զրոյական իմպուլս։ Իմպուլսի պահպանման օրենքը պահանջում է ընդհանուր զրո իմպուլս ունեցող առնվազն երկու ֆոտոնի մասնակցություն, իսկ ֆոտոնների էներգիան, հետևաբար` նաև հաճախությունը որոշվում են էներգիայի պահպանման օրենքից։ Անիհիլյացիայի պրոցեսը գերիշխող է նյութի միջով բարձր էներգիա ունեցող գամմա ճառագայթման տարածման ժամանակ
- ↑ Taylor, G. I. (1909). «Interference fringes with feeble light». Proceedings of the Cambridge Philosophical Society. 15: 114–115. (անգլերեն)
- ↑ The Feynman Lectures on Physics Vol. I Ch. 38: The Relation of Wave and Particle Viewpoints
- ↑ տե՛ս օրինակ էջ. 10f, Schiff, L. I. (1968). Quantum Mechanics (3rd ed.). McGraw-Hill. 0070552878.
- ↑ Kramers, H. A. (1958). Quantum Mechanics. Amsterdam: North-Holland. (անգլերեն)
- ↑ Bohm, D. (1989) [1954]. Quantum Theory. Dover Publications. ISBN 0-486-65969-0. (անգլերեն)
- ↑ Newton, T. D.; Wigner, E. P. (1949). «Localized states for elementary particles». Reviews of Modern Physics. 21: 400–406. doi:10.1103/RevModPhys.21.400. (անգլերեն)
- ↑ §5 c.29 Берестецкий, Е. М.; Лифшиц, Е. М. Питаевский, Л. П. (2002). Теоретическая физика.IV.Квантовая электродинамика. ФИЗМАТЛИТ. ISBN 5-9221-0058-0.
{{cite book}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (ռուս.) - ↑ Bialynicki-Birula, I. (1994). «On the wave function of the photon». Acta Physica Polonica A. 86: 97–116. (անգլերեն)
- ↑ Sipe, J. E. (1995). «Photon wave functions». Physical Review A. 52: 1875–1883. doi:10.1103/PhysRevA.52.1875. (անգլերեն)
- ↑ Bialynicki-Birula, I. (1996). «Photon wave function». Progress in Optics. 36: 245–294. doi:10.1016/S0079-6638(08)70316-0. (անգլերեն)
- ↑ Scully, M. O.; Zubairy, M. S. (1997). Quantum Optics. Cambridge (UK): Cambridge University Press. ISBN 0-521-43595-1. (անգլերեն)
- ↑ Bose, S. N. (1924). «Plancks Gesetz und Lichtquantenhypothese». Zeitschrift für Physik. 26: 178–181. doi:10.1007/BF01327326.
- ↑ А. С. Василевский, В. В. Мултановский, Статистическая физика и термодинамика, М., Просвещение, 1985, ст. 163-167
- ↑ Einstein A. (1924). «Quantentheorie des einatomigen idealen Gases». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. 1924: 261–267.
- ↑ Einstein A. (1925). «Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. 1925: 3–14.
- ↑
Anderson, M. H.; Ensher, J. R.; Matthews, M. R.; Wieman, C. E.; Cornell, E. A. (1995). «Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor». Science. 269: 198–201. doi:10.1126/science.269.5221.198. PMID 17789847.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (անգլերեն) - ↑ Streater, R. F.; Wightman, A. S. (1989). PCT, Spin and Statistics, and All That. Addison-Wesley. ISBN 020109410X. (անգլերեն)
- ↑ Section 1.4 in Wilson, J.; Hawkes, F. J. B. (1987). Lasers: Principles and Applications. New York: Prentice Hall. ISBN 0-13-523705-X. (անգլերեն)
- ↑ P. 322 in Einstein A. (1916a). «Strahlungs-emission und -absorption nach der Quantentheorie». Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318–323.:

Die Konstanten and würden sich direkt berechnen lassen, wenn wir im Besitz einer im Sinne der Quantenhypothese modifizierten Elektrodynamik und Mechanik wären." 
- ↑ Dirac P. A. M. (1926). On the Theory of Quantum Mechanics. Vol. 112. էջեր 661–677. doi:10.1098/rspa.1926.0133.
{{cite book}}: Unknown parameter|book-title=ignored (օգնություն) (անգլերեն) - ↑ 57,0 57,1 Dirac P. A. M. (1927a). The Quantum Theory of the Emission and Absorption of Radiation. Vol. 114. էջեր 243–265.
{{cite book}}:|journal=ignored (օգնություն) (անգլերեն) - ↑ 58,0 58,1 Dirac P. A. M. (1927b). The Quantum Theory of Dispersion. Vol. 114. էջեր 710–728.
{{cite book}}:|journal=ignored (օգնություն) (անգլերեն) - ↑ Heisenberg W.; Pauli, W. (1929). «Zur Quantentheorie der Wellenfelder». Zeitschrift für Physik. 56: 1. doi:10.1007/BF01340129.
- ↑ Heisenberg W.; Pauli, W. (1930). «Zur Quantentheorie der Wellenfelder». Zeitschrift für Physik. 59: 139. doi:10.1007/BF01341423.
- ↑ Fermi E. (1932). «Quantum Theory of Radiation». Reviews of Modern Physics. 4: 87. doi:10.1103/RevModPhys.4.87. (անգլերեն)
- ↑ Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. ISBN 0-198-53907-X. Արխիվացված է օրիգինալից 2012 թ․ մայիսի 31-ին. Վերցված է 2012 թ․ փետրվարի 23-ին. (անգլերեն)
- ↑ Born M. (1926a). «Zur Quantenmechanik der Stossvorgänge». Zeitschrift für Physik. 37: 863–867. doi:10.1007/BF01397477.
- ↑ Born M. (1926b). «Zur Quantenmechanik der Stossvorgänge». Zeitschrift für Physik. 38: 803. doi:10.1007/BF01397184.
- ↑ Pais, A. (1986). Inward Bound: Of Matter and Forces in the Physical World. Oxford University Press. ISBN 0-198-51997-4. (անգլերեն): Բոռնը հաստատում է, որ ինքը ոգեշնչված էր տեսության զարգացմանը ուղղված Այնշտայնի չհրապարակված աշխատություններով, որում կետանման ֆոտոնները հավանականորեն կառավարվում էին Մաքսվելի հավասարումներին ենթարկվող «ուրվական դաշտերով»։
- ↑ Debye P. (1910). «Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung». Annalen der Physik. 33: 1427–1434. doi:10.1002/andp.19103381617.
- ↑
Born M.; Heisenberg, W.; Jordan, P. (1925). «Quantenmechanik II». Zeitschrift für Physik. 35: 557–615. doi:10.1007/BF01379806.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) - ↑ Статья А. В. Ефремова, Физический энциклопедический словарь, М.: Советская энциклопедия, 1984
- ↑ Статья В. И. Григорьева, Физический энциклопедический словарь, М.: Советская энциклопедия, 1984
- ↑ Photon-photon-scattering section 7-3-1, renormalization chapter 8-2 in Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 0-07-032071-3. (անգլերեն)
- ↑ Weiglein, G. (2008). «Electroweak Physics at the ILC». Journal of Physics: Conference Series. 110: 042033. doi:10.1088/1742-6596/110/4/042033. (անգլերեն)
- ↑ QCD and Two-Photon Physics, in Linear Collider Physics Resource Book for Snowmass 2001, Chapter 7, LC-REV-2001-074-US. (անգլերեն)
- ↑ 73,0 73,1 Ryder, L. H. (1996). Quantum field theory (2nd ed.). Cambridge University Press. ISBN 0-521-47814-6. OCLC 32853321. (անգլերեն)
- ↑ 74,0 74,1 Статья Э. А. Ефремова, Физический энциклопедический словарь, М.: Советская энциклопедия, 1984, ст. 237-239}}
- ↑ Sheldon Glashow Nobel lecture, delivered 8 December 1979.
- ↑ Abdus Salam Nobel lecture, delivered 8 December 1979.
- ↑ Steven Weinberg Nobel lecture, delivered 8 December 1979.
- ↑ Глава 14 в Hughes, I. S. (1985). Elementary particles (2nd ed.). Cambridge University Press. ISBN 0-521-26092-2. (անգլերեն)
- ↑ Раздел 10.1 в Dunlap, R. A. (2004). An Introduction to the Physics of Nuclei and Particles. Brooks/Cole. ISBN 0-534-39294-6. (անգլերեն)
- ↑ Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 0-07-032071-3. (անգլերեն)
- ↑ Stephani, H.; Stewart, J. (1990). General Relativity: An Introduction to the Theory of Gravitational Field. Cambridge University Press. ISBN 0-521-37941-5. (անգլերեն)
- ↑ Naeye, R. (1998). Through the Eyes of Hubble: Birth, Life and Violent Death of Stars. CRC Press. ISBN 0-750-30484-7. OCLC 40180195. (անգլերեն)
- ↑ Patterson, J. D.; Bailey, B. C. (2007). Solid-State Physics: Introduction to the Theory. Springer. ISBN 3-540-24115-9. (անգլերեն)
- ↑ Ch 4 in Hecht, Eugene (2001). Optics. Addison Wesley. ISBN 9780805385663. (անգլերեն)
- ↑ Е. Б. Александров, В. С. Запасский. «Медленный свет: за фасадом сенсации». Элементы.Ру. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 21-ին. Վերցված է 2009 թ․ ապրիլի 5-ին.
- ↑ Kitchin, C.R. (2008). Astrophysical Techniques. Boca Raton (FL): CRC Press. ISBN 1-4200-8243-4.
- ↑ Jennewein, T.; Achleitner, U.; Weihs, G.; Weinfurter, H.; Zeilinger, A. (2000). «A fast and compact quantum random number generator». Review of Scientific Instruments. 71: 1675–1680. doi:10.1063/1.1150518. (անգլերեն)
- ↑ Stefanov, A.; Gisin, N.; Guinnard, O.; Guinnard, L.; Zbiden, H. (2000). «Optical quantum random number generator». Journal of Modern Optics. 47: 595–598. doi:10.1080/095003400147908. (անգլերեն)
- ↑ Համարվում է, որ ֆոտոնը «զանգված չունի», սակայն պետք է հիշել, որ այս պնդումը վերաբերում է միայն հանգստի զանգվածին, որն իսկապես զրո է։ Սակայն ֆոտոնն ունի ռելյատիվիստական զանգված։ Մասնավորապես, դրա մասին է խոսում այն փաստը, որ ֆոտոնների տեսքով էներգիայի ճառագայթման արդյունքում Արեգակի զանգվածը փոքրանում է։ Հենց հանգստի զանգված չունենալու պատճառով է, որ ֆոտոնը ստիպված է վակուումում շարժվել հնարավոր առավելագույն` լույսի արագությամբ։ Ֆոտոնը կարող է գոյություն ունենալ միայն այդ շարժման մեջ։ Ֆոտոնի որևէ կանգ համարժեք է նրա կլանմանը
- ↑ G. Spavieri and M. Rodriguez (2007). «Photon mass and quantum effects of the Aharonov-Bohm type». Physical Review A. 75: 052113. doi:10.1103/PhysRevA.75.052113. (անգլերեն)
- ↑ Goldhaber, A. S. (1971). «Terrestrial and Extraterrestrial Limits on The Photon Mass». Reviews of Modern Physics. 43: 277–296. doi:10.1103/RevModPhys.43.277. (անգլերեն)
- ↑ Fischbach, E.; Kloor, H.; Langel, R. A.; Lui, A. T. Y.; Peredo, M. (1994). «New Geomagnetic Limits on the Photon Mass and on Long-Range Forces Coexisting with Electromagnetism». Physical Review Letters. 73: 514–517. doi:10.1103/PhysRevLett.73.514.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (անգլերեն) - ↑ Official particle table for gauge and Higgs bosons S. Eidelman et al. (Particle Data Group) Physics Letters B 592, 1 (2004)
- ↑ Davis, L.; Goldhaber, A. S.; Nieto, M. M. (1975). «Limit on Photon Mass Deduced from Pioneer-10 Observations of Jupiter's Magnetic Field». Physical Review Letters. 35: 1402–1405. doi:10.1103/PhysRevLett.35.1402.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (անգլերեն) - ↑ Luo, J.; Shao, C. G.; Liu, Z. Z.; Hu, Z. K. (1999). «Determination of the limit of photon mass and cosmic magnetic vector with rotating torsion balance». Physical Review A. 270: 288–292.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (անգլերեն) - ↑ Schaeffer, B. E. (1999). «Severe limits on variations of the speed of light with frequency». Physical Review Letters. 82: 4964–4966. doi:10.1103/PhysRevLett.82.4964. (անգլերեն)
- ↑ Luo, J.; Tu, L. C.; Hu, Z. K.; Luan, E. J. (2003). «New experimental limit on the photon rest mass with a rotating torsion balance». Physical Review Letters. 90: Art. No. 081801. doi:10.1103/PhysRevLett.90.081801.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (անգլերեն) - ↑ Williams, E. R.; Faller, J. E.; Hill, H. A. (1971). «New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass». Physical Review Letters. 26: 721–724. doi:10.1103/PhysRevLett.26.721.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) (անգլերեն) - ↑ Lakes, R. (1998). «Experimental Limits on the Photon Mass and Cosmic Magnetic Vector Potential». Physical Review Letters. 80: 1826. doi:10.1103/PhysRevLett.80.1826. (անգլերեն)
- ↑ 2006 PDG listing for photon W.-M. Yao et al. (Particle Data Group) Journal of Physics G 33, 1 (2006).
- ↑ Adelberger, E.; Dvali, G.; Gruzinov, A. (2007). «Photon Mass Bound Destroyed by Vortices». Physical Review Letters. 98: Art. No. 010402. doi:10.1103/PhysRevLett.98.010402.
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) - ↑ Official particle table for gauge and Higgs bosons Retrieved 24 October 2006
- ↑ Алексей Паевский. «Телепортация вышла на поток». Gazeta.ru. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 21-ին. Վերցված է 2009 թ․ ապրիլի 19-ին.
- ↑ Физика квантовой информации, Под ред. Д. Боумейстера, А. Экерта, А. Цайлингера, М., Постмаркет, 2002, ст. 79-85
- ↑ Мария Чехова. «Квантовая оптика». Кругосвет. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 21-ին. Վերցված է 2009 թ․ ապրիլի 19-ին.
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
| Վիքիպահեստ նախագծում կարող եք այս նյութի վերաբերյալ հավելյալ պատկերազարդում գտնել Ֆոտոն կատեգորիայում։ |
|
|
Այս հոդվածը ներառված է Հայերեն Վիքիպեդիայի լավ հոդվածների ցանկում |
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 12, էջ 692)։ |
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի օրվա հոդված: |
















































































