Մաքսվելի հավասարումներ
| Էլեկտրամագնիսականություն |
|---|
| Մագնիսականություն |

Մաքսվելի հավասարումներ, դիֆերենցիալ կամ ինտեգրալ հավասարումների համակարգ, որը բնութագրում է էլեկտրամագնիսական դաշտը վակուումում և նրա կապը էլեկտրական լիցքերի և հոսանքների հետ։ 19-րդ դարի կեսերին կուտակված փորձերի հիման վրա Ջեյմս Կլերկ Մաքսվելի կողմից ձևակերպված հավասարումները որոշիչ դեր խաղացին ինչպես էլեկտրամագնիսականության հետ անմիջականորեն կապ ունեցող ֆիզիկայի բնագավառներում, այնպես էլ բազմաթիվ հիմնարար տեսություններում, որոնք չեն առնչվում էլեկտրամագնիսականությանը։
Պատմություն[խմբագրել | խմբագրել կոդը]
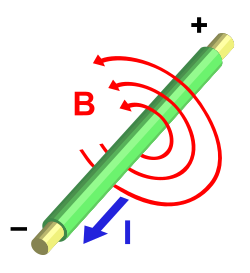

Մաքսվելի ձևակերպած հավասարումների հիմք են հանդիսացել XIX դարի սկզբում կատարված մի շարք կարևոր փորձարարական բացահայումներ։ 1820 թվականին Հանս Քրիստիան Էրստեդը հայտնաբերեց, որ հաղորդալարի միջով անցնող գալվանական հոսանքը շեղում է կողմնացույցի սլաքը։ Այդ հայտնագործությունը գրավեց ժամանակաշրջանի գիտնականների ուշադրությունը։ Հենց 1820 թվականին Բիոն և Սավարը հոսանքի հետևանքով առաջացած մագնիսական ինդուկցիան անվանեցին «Բիո-Սավարի օրենք», իսկ Ամպերը հայտնաբերեց, որ այն գոյանում է երկու հաղորդալարերի միջև եղած տարածության մեջ, եթե հաղորդալարերով հոսանք է անցնում։ Ամպերը ներմուծեց «էլեկտրադինամիկական» տերմինը և առաջ քաշեց հիպոթեզ, որ մագնիսական դաշտը մրրկային է։
Էրստեդի հայտնագործությունը, թե հոսանքը ազդում է մագնիսի վրա, Մայքլ Ֆարադեյին հանգեցրեցին այն մտքին, որ հակառակ երևույթը ևս պետք է գոյություն ունենա՝ մագնիսը պետք է ազդեցություն թողնի հոսանքի վրա։ Երկար փորձերից հետո Ֆարադեյին հաջողվեց ապացուցել, որ եթե հաղորդչի մոտ մագնիսը շարժվի, ապա կառաջանա էլեկտրական հոսանք։ Այս երևույթը անվանվեց էլեկտրական ինդուկցիա։ Ֆարադեյի հայտնագործությունները մեծ հետք թողեցին Մաքսվելի աշխատանքների վրա։
Դիֆերենցիալ տեսքը[խմբագրել | խմբագրել կոդը]
Միջավայրում էլեկտրամագնիսական երևույթները նկարագրող ֆիզիկական մեծությունները ենթարկվում են Մաքսվելի հավասարումներով տրված օրենքներին։
| Անվանում | Դիֆերենցիալ տեսք | Ֆիզիկական իմաստ |
|---|---|---|
| Ամպերի օրենք |
|
Մագնիսական դաշտը մրրկային է։ |
| Էլեկտրամագնիսական ինդուկցիայի Ֆարադեյի օրենք |
|
Մրրկային էլեկտրական դաշտն առաջանում է ժամանակի ընթացքում փոփոխվող մագնիսական դաշտից։Մրրկային էլեկտրական դաշտի ուժագծերը փակ են։ |
| Կուլոնի օրենք |
|
էլեկտրական դաշտը գոյանում է էլեկտարական լիցքերի առկայությամբ։ Վերջինս մրրկային չէ, ուժագծերը փակ չեն, սկսվում են դրական ու վերջանում բացասական լիցքերի վրա։ |
| Մագնիսական դաշտի ուժագծերի անխզելիության օրենք |
|
Մագնիսական դաշտն ակունքներ չունի, ուժագծերը փակ են։ |
Նշանակումներ՝
- ― լիցքի խտություն
- ― հոսանքի խտություն
- ― լույսի արագությունը վակուումում
- ― էլեկտրական դաշտի լարվածություն
- ― մագնիսական դաշտի լարվածություն
- ― էլեկտրական ինդուկցիա
- ― մագնիսական ինդուկցիա
- ― վեկտորի ռոտոր
- ― վեկտորի դիվերգենցիա
Ինտեգրալային տեսքը[խմբագրել | խմբագրել կոդը]
Գաուսի և Ստոքսի բանաձևերից կարելի է տալ Մաքսվելի հավասարումների ինտեգրալային տեսքը՝
| Անվանում | Ինտեգրալային տեսքը |
|---|---|
| Գաուսի օրենք |
|
| Գաուսի օրենքը մագնիսական դաշտի համար |
|
| Էլեկտրամագնիսական ինդուկցիայի օրենք |
|
| Մագնիսական դաշտի շրջապտույտի թեորեմ |
|

- — ծավալում էլեկտրական լիցք
- — մակերեսով անցնող էլեկտրական հոսանք
























