Ալիքային ֆունկցիա

Հարմոնիկ տատանակի ալիքային ֆունկցիայի իրական (կապույտ) և կեղծ (կարմիր) բաղադրիչները: C,D,E,F հետագծերը կանգուն ալիքներ են (ստացիոնար վիճակներ)՝ ի տարբերություն G կամ H դեպքերի: Կանգուն ալիքի հաճախությունը համեմատական է տատանակի էներգիական մակարդակի հնարավոր էներգիային: Էներգիայի այսպիսի «քվանտացումը» տեղի չի ունենում դասական ֆիզիկայում, որտեղ տատանակը կարող է ցանկացած էներգիա ունենալ:

Ալիքային ֆունկցիան քվանտամեխանիկական հավանականությունների ամպլիտուդն է, որը նկարագրում է մասնիկի քվանտային վիճակը և վարքը: Որպես կանոն, այն կոմպլեքս փոփոխականի ֆունկցիա է: Քանի որ Շրեդինգերի հավասարումը մաթեմատիկորեն ալիքային հավասարման տեսակ է, ալիքային ֆունկցիայի վարքը որակապես հիշեցնում է այլ ալիքներ, ինչպես օրինակ ջրի ալիքները կամ լարի ալիքներ: Անվանումը գալիս է այդտեղից:

Ընդունված է ալիքային ֆունկցիան նշանակել հունարեն «փսի» տառով՝ ψ կամ Ψ (փոքրատառ կամ մեծատառ): Չնայած ψ-ն կոմպլեքս թիվ է, |ψ|²-ն իրական է: Այն տվյալ պահին տվյալ վայրում մասնիկի գտնվելու հավանականության խտությունն է:

Միավորների միջազգային համակարգում ψ-ի միավորը կախված է համակարգից: Եռաչափ դեպքում մեկ մասնիկի համար այն m^–3/2 է: Չափողականություն չունեցող այս միավորը հետևանք է այն հանգամանքի, որ |ψ|²-ի ինտեգրալը եռաչափ տարածության տիրույթում չափողականություն չունեցող հավանականություն է (հավանականություն, որ մասնիկը գտնվում է այդ տիրույթում): Տարբեր թվով մասնիկների և չափումների համար այդ միավորները կարող են տարբեր լինել:

Ալիքային ֆունկցիան քվանտային մեխանիկայի առանցքային հասկացությունն է: Նրանից են բխում քվանտային մեխանիկայի փիլիսոփայական դժվարությունները և խորհրդավոր հետևանքները, հարցերը, թե ինչ իմաստ ունի քվանտային մեխանիկան բնության մեջ և թե ինչպիսին է բնության վարքը ատոմական և ավելի փոքր սանդղակներում. հարցեր, որ այսօր էլ վիճելի են:

Պատմությունը

1920-1930-ական թթ. քվանտային մեխանիկան ձևավորվեց երկու տարբեր ճյուղերով՝ հաշվարկների (Լուի դը Բրոյլ, Էրվին Շրեդինգեր, Պոլ Դիրակ և այլք ) և գծային հանրահաշվի (Վերներ Հայզենբերգ, Մաքս Բոռն, Վոլֆգանգ Պաուլի) ճանապարհով: Առաջին ճյուղը հայտնի դարձավ «ալիքային մեխանիկա» անունով, երկրորդը՝ «մատրիցային մեխանիկա»: Շրեդինգերը ցույց տվեց, որ այդ երկու մոտեցումները համարժեք են:

1925թ. դը Բրոյլը ձևակերպեց կապը ալիքի երկարության և իմպուլսի մոմենտի միջև, որն այժմ հայտնի է դը Բրոյլի հավասարում անունով: Շրեդինգերը սկսեց հավասարում փնտրել դը Բրոյլի ալիքը նկարագրելու համար, և 1926թ. հրապարակեց այն: Այդ հավասարումը հիմնված էր դասական մեխանիկայի էներգիայի փոխակերպման վրա: Այժմ այն կոչվում է Շրեդինգերի հավասարում: Սակայն ոչ ոք, նույնիսկ Շրեդինգերը և դը Բրոյլը, չկարողացան հասկանալ, թե ինչպես կարելի է մեկնաբանել այն և ինչ իմաստ ուներ այդ ֆունկցիան 1924-27թթ. Բորը, Հայզենբերգը և Բոռնը մշակեցին հավանականության լայնույթի գաղափարը, որը հայտնի է քվանտային մեխանիկայի կոպենհագենյան մեկնաբանություն անունով: Քվանտային մեխանիկայի մի շարք մեկնաբանություններ կան, սակայն ամենակարևորը սա է, քանի որ այս ճանապարհով հնարավոր է հասկանալ քվանտային հաշվարկները:

1928թ. Դիրակը, էլեկտրոնի համար արտածեց այս հավասարումը՝ կիրառելով հատուկ հարաբերականության տեսությունը և քվանտային մեխանիկան (Դիրակի հավասարում): Ալիքային ֆունկցիայի անսովոր բնույթը պարզա դարձավ այդ հավասարումից. այն ոչ միայն կոմպլեքս թիվ է, այլև՝ սպինոր , և սպինը ինքնաբերաբար մտնումէ ալիքային ֆունկցիայի հատկությունների մեջ: Չնայած խնդիրներին, Դիրակը ձևակերպեց նաև այդ հավասարման ռելյատիվիստական տարբերակը:

Ալիքային ֆունկցիայի ֆիզիկական իմաստը

Կոօրդինատային պատկերացման համաձայն, $\Psi(x,t)= \langle x\left|\psi(t)\right\rangle$ ալիքային ֆունկցիան՝

$\left|\psi(t)\right\rangle=\int \Psi(x,t)\left|x\right\rangle dx$,

որտեղ $\left|x\right\rangle = \left|x_1, x_2, \ldots , x_n\right\rangle$-ը կոօրդինատային բազիսի վեկտորն է: $\! \Psi(x_1, x_2, \ldots , x_n,t)$-ն կախված է համակարգի կոօրդինատներից (կամ ընդհանրացված կոօրդինատներից): Ֆիզիկական իմաստ ունի ալիքային ֆունկցիայի մոդուլի քառակուսին՝ $\! \left|\Psi(x_1, x_2, \ldots , x_n,t)\right|^2$: Այն համակարգի գտնվելու $~\omega$ հավանականության խտությունն է (դիսկրետ սկեկտրների համար՝ հավանականությունը) $~t$ պահին $\! x_1=x_{01}, x_2=x_{02}, \ldots , x_n=x_{0n}$ կոօրդինատներով նկարագրվող դիրքում.

$~\omega = \frac{dP}{dV} = \left|\Psi(x_1, x_2, \ldots , x_n,t)\right|^2 = \Psi^\ast\Psi$:

$\! \Psi(x_1, x_2, \ldots , x_n,t)$ նկարագրվող համակարգի տրված քվանտային վիճակի համար , $~P$ հավանականությունը, որ մասնիկը կգտնվի տարածության $~V$ վերջավոր ծավալով կամայական տիրույթում՝ $P={\int{dP}}={\int\limits_{V} {\omega}dV}={\int\limits_{V}{\Psi^\ast\Psi}dV}$     $~(1)$:

Ալիքային ֆունկցիային ներկայացվող պահանջները

Ալիքային ֆունկցիայի հավանակային իմաստը քվանտային մեխանիկայի շրջանակներում որոշակի սահմանափակումներ կամ պայմաններ է դնում ալիքային ֆունկցիայի վրա: Այդ ստանդարտ պայմանները կոչվում են ալիքային ֆունկցիայի կանոնավորության պայմաններ: Դրանք են.

1. Ալիքային ֆունկցիայի վերջավորության պայմանը: Ալիքային ֆունկցիան չի կարող ընդունել անվերջ արժեքներ, այնպիսին, որ $~(1)$ իտնեգրալը տարամետ դառնա: Ուստի այն պայմանը պահանջում է, որ ալիքային ֆունկցիան լինի քառակուսային ինտեգրելի ֆունկցիա: Մասնավորապես, նորմավորված ալիքային ֆունկցիայի խնդիրներում ալիքային ֆունկցիայի մոդուլի քառակուսին անվերջությունում պետք է ձգտի զրոյի:
2. Ալիքային ֆունկցիայի միարժեքության պայմանը: Ալիքային ֆունկցիան պետք է միարժեք ֆունկցիա լինի կոօրդինատներից և ժամանակից, քանի որ մասնիկի հայտնաբերման հավանականության խտությունը յուրաքանչյուր խնդրում պետք է միարժեքորեն որոշվի: Գլանային կամ գնդային կոօրդինատական համակարգում դիտարկելիս միարժեքության պայմանը հանգեցնում է ըստ անկյունային փոփոխականների ալիքային ֆունկցիայի պարբերականության:
3. Ալիքային ֆունկցիայի անընդհատության պայմանը: Ժամանակի ցանկացած պահին ալիքային ֆունկցիան պետք է անընդհանտ ֆունկցիա լինի տարածական կոօրդինատներից: Բացի այդ, անընդհատ պետք է լինեն նաև ալիքային ֆունկցիայի մասնակի ածանցյալները՝ $~\frac{\partial \Psi}{\partial x}$, $~\frac{\partial \Psi}{\partial y}$, $~\frac{\partial \Psi}{\partial z}$: Այս մասնակի ածանցյալները միայն իդեալական ուժային դաշտերի բացառիկ դեպքերում կարող են խզում ունենալ տարածության այն կետերում, որտեղ ուժային դաշտը (որտեղ շարժվումէ մասնիկը) նկարագրող պոտենցիալ էներգիան ունի երկրորդ սեռի խզում:

Ալիքային ֆունկցիայի անընդհատությունը և առաջին տարածական ածանցյալը (x ուղղությամբ, y և z կոօրդինատները պատկերված չեն) t պահին:

Եթե այս պահանջները չեն բավարարվում, ալիքային ֆունկցիան հնարավոր չէ մեկնաբանել որպես հավանականության ամպլիտուդ, ալիքային ֆունկցիայի և նրա առաջին կարգի ածանցյալների արժեքները չեն կարող լինել վերջավոր և որոշված, այսինքն՝ հավանականությունները կարող են լինել անսահման և ոչ միարժեք որևէ դիրքում և ժամանակի որևէ պահին, ինչն անհեթեթություն է, քանի որ չի բավարարում հավանականության աքսիոմներին: Առանց այս պահանջներին բավարարելու հնարավոր չէ նաև դիտարկվող քվանտային համակարգի չափումներ անցկացնել, քանի որ այն կարող է լինել անսահման և ունենալ մի քանի արժեքներ:

Նորմավորման պայմաններ

$\! \Psi$ ֆունկցիան իր իմաստին համապատասխան պետք բավարարի նորմավորման պայմանին, օրինակ, կոօրդինատային պատկերացման մեջ այն պետք է ունենա հետևյալ տեսքը՝

${\int\limits_{-\infty}^{+\infty} {|\Psi|}^2 d^{3}\textbf{r}}=1$

Ալիքային ֆունկցիայի նորմավորման պայմանը արտահայտում է այն փաստը, որ տրված ալիքային ֆունկցիայով մասնիկի հայտնաբերման հավանականությունը ամբողջ տարածության մեջ հավասար է մեկի: Ընդհանուր դեպքում ինտեգրումը պետք է կատարվի ըստ բոլոր փոփոխականների, որոնցից կախված է ալիքային ֆունկցիան տրված պատկերացման համաձայն:

Քվանտային վիճակների վերադրման սկզբունքը

Վերադրման սկզբունքի համաձայն, եթե համակարգը կարող է գտնվել $\! \Psi_1$ և $\! \Psi_2$ ալիքային ֆունկցիաներով նկարագրվող վիճակում, ապա յան կարող է գտնվել նաև $\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2$

ալիքային ֆունկցիայով նկարագրվող վիճակում: $\! c_1$-ն և $\! c_2$-ն կամայական կոմպլեքս թվեր են:

Ակնհայտ է, որ կարելի է խոսել ցանկացած թվով քվանտային վիճակների վերադրման մասին, այսինքն՝ համակարգի այնպիսի քվանտային վիճակի մասին, որը նկարագրվում է $\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2 + \ldots + {c}_N{\Psi}_N=\sum_{n=1}^{N} {c}_n{\Psi}_n$ ալիքային ֆունկցիայով:

Այս վիճակում $~{c}_n$ գործակցի մոդուլի քառակուսին որոշում է հավանականությունը, որ չափման դեպքում համակարգը կլինի $~{\Psi}_n$ ֆունկցիայով նկարագրվող վիճակում:

Այդ պատճառով նորմավորված ալիքային ֆունկցիայի համար $~\sum_{n=1}^{N}\left|c_{n}\right|^2=1$:

Սահմանումը տարբեր դեպքերում

Զրո սպին ունեցող մեկ մասնիկի միաչափ դեպքը

Կոօրդինատային ալիքային ֆունկցիա

Դիտարկենք սպին չունեցող մեկ մասնիկի պարզագույն՝ միաչափ դեպքը: Նման մասնիկի վիճակը նկարագրվում է

$\Psi(x,t)$

ալիքային ֆունկցիայով, որտեղ x-ը կոօրդինատն է, t-ն՝ ժամանակը: Այս ֆունկցիան կոմպլեքս թիվ է: $\Psi(x,t)$-ն կոմպլեքս փոփոխականի ֆունկցիա է:

Եթե մասնիկի հնարավոր է չափել մասնիկի կոօրդինատը, ապա նրա գտնվելու վայրը որոշակի չէ, այլ նկարագրվում է հավանակային բաշխումով: Հավանականությունը, որ x կոօրդինատը կգտնվի [a, b] միջակայքում (a ≤ x ≤ b)՝

$P_{a<x<b} = \int\limits_a^b |\Psi(x,t)|^2 \,\mathrm{d}x$

է, որտեղ t-ն չափման ժամանակն է: Այլ կերպ ասած, $|\Psi(x,t)|^2$-ն այն հավանականության խտությունն է, որ մասնիկը ավելի շուտ կգտնվի x կետում, քան այլ տեղ:

Դա բերում է նորմավորման պայմանի՝

$\int\limits_{-\infty}^\infty |\Psi(x,t)|^2\, \mathrm{d}x = 1$,

այսինքն՝ եթե հնարավոր են չափումներ, ապա կարելի է ասել, որ մասնիկը 100% հավանականությամբ գտնվում է ինչ-որ տեղ:

Իմպուլսային տարածության ալիքային ֆունկցիա

Իմպուլսային տարածությունում նույնպես մասնիկը ունի ալիքային ֆունկցիա՝

$\Phi(p,t)$,

որտեղ p-ն իմպուլսն է մեկ ուղղության վրա և կարող է ընդունել $-\infty$-ից $+\infty$ ցանկացած արժեք, t-ն ժամանակն է: Եթե մասնիկի իմպուլսը հնարավոր է չափել, արդյունքը նկարագրվում է հավանակային բաշխումով, ինչպես նախորդ դեպքում՝

$P_{a<p<b} = \int\limits_a^b |\Phi(p,t)|^2 \mathrm{d}p$:

Նորմավորման պայմանը ևս նման է նախորդ դեպքին՝

$\int\limits_{-\infty}^{\infty} \left | \Phi \left ( p, t \right ) \right |^2 \mathrm{d}p = 1:$

Կապը ալիքային ֆունկցիաների միջև

Կոօրդինատային և իմպուլսային տարածությունների ալիքային ֆունկցիաներըը մեկը մյուսի Ֆուրիեի ձևափոխություններն են, հետևաբար երկուսն էլ պարունակում են միևնույն ինֆորմացիան և դրանցից միայն մեկը բավարար չէ մասնիկի որևէ հատկություն հաշվարկելու համար: Միաչափ դեպքում

$\begin{align} \Phi(p,t) & = \frac{1}{\sqrt{2\pi\hbar}}\int\limits_{-\infty}^\infty e^{-ipx/\hbar} \Psi(x,t)\mathrm{d}x \\ &\upharpoonleft \downharpoonright\\ \Psi(x,t) & = \frac{1}{\sqrt{2\pi\hbar}}\int\limits_{-\infty}^\infty e^{ipx/\hbar} \Phi(p,t)\mathrm{d}p . \end{align}$

Երբեմն p իմպուլսի փոխարեն օգտագործվում է k ալիքային վեկտորը, քանի որ դրանք կապված են դը Բրոյլի առնչություններով՝

$p = \hbar k:$

Համապատասխան տարածությունը կոչվում է k-տարածություն: . Քանի որ p-ն և k-ն հաստատունի ճշտությամբ համարժեք են, տարբերություն չկա, դե դրանցից որն է օգտագործվում: Գործնականում առավել հաճախ կիրառվում է կոօրդինատային տարածության ալիքային ֆունկցիան

0 սպինով մասնիկի ալիքային ֆունկցիան միաչափ դեպքում: Պատկերված ալիքային ֆունկցիաները անընդհատ են, վերջավոր, միարժեք և նորմավորված: Մասնիկների թափանցիկության աստիճանը (%) համապատասխանում է x առանցքի վրա տվյալ կետում մասնիկի գտնվելու հավանականության խտությանը (ինչը կարելի է արտահայտել %-ով): 1. Ալիք-մասնիկի «դադարի» վիճակը: 2. Ներքևում՝ ալիք-մասնիկը շարժման մեջ

Ալիք-մասնիկը շարժման մեջ

Նորմավորման պայմաններ

1D տիրույթում x = 0 և x = L-ով սահմանափակված մասնիկի ալիքային ֆունկցիան՝

$\begin{align} \Psi (x,t) & = Ae^{i(kx-\omega t)}, & x \in [0,L] \\ \Psi (x,t) & = 0, & x \notin [0,L] \\ \end{align}$:

Նորմավորելու համար պետք է գտնենք A կամայական հաստատունի արժեքը, որը հաշվարկվում է

$\int\limits_{-\infty}^{\infty} |\Psi|^2 {\rm d}x = 1$-ից:

Ψ-ից ունենք |Ψ|²;

$| \Psi | ^2 = A^2 e^{i(kx - \omega t)} e^{-i(kx - \omega t)} =A^2 ,$

Այնպես որ ինտեգրալը դառնում է

$\int\limits_{-\infty}^0 0 {\rm d}x + \int\limits_0^L A^2 {\rm d}x + \int\limits_L^\infty 0 {\rm d}x = 1 ,$

ուստի հաստատունը՝

$A^2 L = 1 \rightarrow A = \frac{1}{\sqrt{L}} .$

Նորմավորված ալիքային ֆունկցիան (տրված տիրույթում)՝

$\Psi (x,t) = \frac{1}{\sqrt{L}} e^{i(kx-\omega t)}, \quad x\in[0,L].$

0 սպին ունեցող մի քանի մասնիկները միաչափ դեպքում

Նախորդ ալիքային ֆունկցիան կարելի է ընդհանրացնել N մասնիկների միաչափ դեպքի համար՝

$\Psi(x_1,x_2,\cdots x_N, t)$:

Հավանականությունը, որ 1 մասնիկը R₁ = [a₁,b₁] միջակայքում է, 2 մասնիկը՝ R₂ = [a₂,b₂] միջակայքում և այլն, N մասնիկը՝ R_N = [a_N,b_N] միջակայքում, ,եթե բոլոր չափումներն իրականացվում են միաժամանակ tպահին՝

$P_{x_1\in R_1,x_2\in R_2 \cdots x_N\in R_N} = \int\limits_{a_1}^{b_1} \mathrm{d}x_1 \int\limits_{a_2}^{b_2} \mathrm{d}x_2 \cdots \int\limits_{a_N}^{b_N} \mathrm{d}x_N | \Psi(x_1 \cdots x_N,t)|^2$

Նորմավորման պայմանը կդառնա՝

$\int\limits_{-\infty}^\infty \mathrm{d}x_1 \int\limits_{-\infty}^\infty \mathrm{d}x_2 \cdots \int\limits_{-\infty}^\infty \mathrm{d}x_N |\Psi(x_1 \cdots x_N,t)|^2 = 1$:

N միաչափ ինտեգրալներից յուրաքանչյուրը մեկ մասնիկի համար է:

Երկու 0 սպինով մասնիկների ալիքային ֆունկցիաների պատկերումը միաչափ դեպքում: Վերևում. Մասնիկները փոխազդում են և հեռանում միմյանցից 100% որոշակիությամբ: Այս իրավիճակն ի հայտ է գալիս քվանտային խճճվածության դեպքում:Ներքևում. Մասնիկները շարժման մեջ

0 սպինով մեկ մասնիկը եռաչափ դեպքում

Կոօրդինատային տարածության ալիքային ֆունկցիա

Էլեկտրոնի հավանակային խտությունը ջրածնի ատոմում, տարբեր ուղեծրերի դեպքում

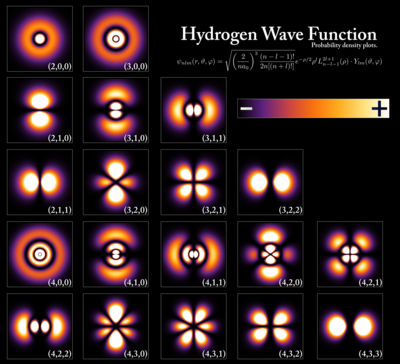
Եռաչափ դեպքում մեկ մասնիկի ալիքային ֆունկցիան համանման է վերը նկարագրված միաչափ դեպքին՝

$\Psi(\mathbf{r},t)$

որտեղ r-ը մասնիկի դիրքն է եռաչափ տարածության մեջ (r –ով նշանակված է (x,y,z), ը), իսկ t-ն ժամանակն էԻնչպես միշտ, $\Psi(\mathbf{r},t)$-ն կոմպլեքս թիվ է: Եթե մասնիկի դիրքը չափվում է t պահին, ապա R տիրույթում գտնվելու հավանականությունը եռաչափ ինտեգրալ է ըստ R տիրույթի՝

$P_{\mathbf{r}\in R} = \int\limits_R \left |\Psi(\mathbf{r},t) \right |^2 \mathrm{d}^3\mathbf{r}$

d³r ծավալային էլեմենտը երբեմն գրվում է նաև "dV" կամ "dx dy dz": Նորմավորման պայմանը՝

$\int\limits_{{\rm all \, space}} \left | \Psi(\mathbf{r},t)\right |^2 \mathrm{d}^3\mathbf{r} = 1,$

Որտեղ բոլոր ինտեգրալները եռաչափ դեպքի համար են:

Իմպուլսային տարածության ալիքային ֆունկցիան

Եռաչափ իմպուլսային տարածության ալիքային ֆունկցիան՝

$\Phi(\mathbf{p},t)$

որտեղ p-ն իմպուլսն է եռաչափ տարածության մեջ, իսկ t-ն՝ ժամանակը: Իմպուլսի երեք բաղադրիչները x, y, z դեկարտյան կոօրդինատական համակարգում յուրաքանչյուր ուղղությամբ կարող են ունենալ $-\infty$-ից մինչև $+ \infty$:

p_x , p_y , p_z իմպուլսի բաղադրիչների չափելու հավանականությունը համապատասխանաբար a և b, c և d, e և f միջև տրվում է

$P_{p_x\in[a,b],p_y\in[c,d],p_z\in[e,f]} = \int\limits_e^f \int\limits_c^d \int\limits_a^b \left | \Phi \left ( \mathbf{p}, t \right ) \right |^2 \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z ,$

բանաձևով, որտեղից նորմավորումը՝

$\int\limits_{{\rm all \, space}} \left | \Phi \left ( \mathbf{p}, t \right ) \right |^2 \mathrm{d}^3\mathbf{p} = 1:$

Ինչպես կոօրդինատային դեպքում, d³p = dp_xdp_ydp_z-ն եռաչափ իմպուլսային տարածության ծավալի էլեմենտն է:

Կապը ալիքային ֆունկցիաների միջև

Նախորդ երկու դեպքերի Ֆուրիեի ձևափոխությունների համար կունենանք

$\begin{align} \Phi(\mathbf{p},t) & = \frac{1}{\sqrt{\left(2\pi\hbar\right)^3}}\int\limits_{{\rm all \, space}} e^{-i \mathbf{r}\cdot \mathbf{p} /\hbar} \Psi(\mathbf{r},t)\mathrm{d}^3\mathbf{r} \\ &\upharpoonleft \downharpoonright\\ \Psi(\mathbf{r},t) & = \frac{1}{\sqrt{\left(2\pi\hbar\right)^3}}\int\limits_{{\rm all \, space}} e^{i \mathbf{r}\cdot \mathbf{p} /\hbar} \Phi(\mathbf{p},t)\mathrm{d}^3\mathbf{p}. \end{align}$

0 սպինով բազմաթիվ մասնիկները եռաչափ դեպքում

Բազմաթիվ մասնիկները որպես կանոն նկարագրվում են մեկ ալիքային ֆունկցիայով: Այս փաստը, որ մեկ ալիքային ֆունկցիան նկարագրում է շատ մասնիկներ, ստեղծում է քվանտային խճճվածություն և ԱՅնշտայն-Պոդոլսկի-Ռոզենի պարադոքսը: Nմասնիկների ալիքային ֆունկցիան՝

$\Psi(\mathbf{r}_1,\mathbf{r}_2 \cdots \mathbf{r}_N,t)$

որտեղ r_i-ն i-րդ մասնիկի դիրքն է եռաչափ տարածությունում, t-ն՝ ժամանակը: Եթե բոլոր մասնիկների դիրքերը միաժամանակ են չափվում t պահին, հավանականությունը, որ 1 մասնիկը R₁ տիրույթում է և 2 մասնիկը՝ R₂ տիրույթում, և այլն, կլինի՝

$P_{\mathbf{r}_1\in R_1,\mathbf{r}_2\in R_2 \cdots \mathbf{r}_N\in R_N} = \int\limits_{R_1} \mathrm{d}^3\mathbf{r}_1 \int\limits_{R_2} \mathrm{d}^3\mathbf{r}_2\cdots \int\limits_{R_N} \mathrm{d}^3\mathbf{r}_N |\Psi(\mathbf{r}_1 \cdots \mathbf{r}_N,t)|^2$

Նորմավորման պայմանը՝

$\int\limits_{{\rm all \, space}} \mathrm{d}^3\mathbf{r}_1 \int\limits_{{\rm all \, space}} \mathrm{d}^3\mathbf{r}_2\cdots \int\limits_{{\rm all \, space}} \mathrm{d}^3\mathbf{r}_N |\Psi(\mathbf{r}_1 \cdots \mathbf{r}_N,t)|^2 = 1$

(altogether, this is 3N one-dimensional integrals).

Քվանտային մեխանիկայում հիմնարար տարբերություն կա նույնական մասնիկների և զանազանելի մասնիկների միջև: Օրինակ, ցանկացած երկու էլեկտրոններ միանգամայն անզանազանելի են միմյանցից. Ֆիզիկայի օրենքները թույլ չեն տալիս "տարբերակման նշան" դնել որևէ էլեկտրոնի վրա՝ դրան հետևելու համար : Դա իր հերթին պահանջ է դնում նաև ալիքային ֆւնկցիայի վրա:Օրինակ, եթե 1 և 2 մասնիկները անզանազանելի են, ապա

$\Psi \left (\mathbf{r},\mathbf{r'},\mathbf{r}_3,\mathbf{r}_4,\cdots \right ) = \pm \Psi \left ( \mathbf{r'},\mathbf{r},\mathbf{r}_3,\mathbf{r}_4,\cdots \right )$

որտեղ + նշանի դեպքը վերաբերում է բոզոններին, իսկ – նշանը դրվում է, եթե մասնիկները ֆերմիոններ են: Ավելի ճշգրիտ պնդումը՝

$\Psi \left ( \mathbf{r},\mathbf{r'},\mathbf{r}_3,\mathbf{r}_4,\cdots \right ) = \left ( -1 \right )^{2s} \Psi \left ( \mathbf{r'},\mathbf{r},\mathbf{r}_3,\mathbf{r}_4,\cdots \right )$

որտեղ s-ը սպինային քվանտային թիվն է.

ամբողջ թիվ բոզոնների համար՝ $s \in \left \{ \pm 1,\pm 2,\pm 3 \cdots \right \},$

կիսաամբողջ թիվ ֆերմիոնների համար՝ $s \in \left \{ \pm \frac{1}{2}, \pm \frac{3}{2} \cdots \right \} :$

Ալիքային ֆունկցիան կոչվում է սիմետրիկ (նշանը չի փոխվում բոզոնների փոխատեղման դեպքում) և հակասիմետրիկ (նշանի փոփոխություն ֆերմիոնների փոխատեղման դեպքում): Ալիքային ֆունկցիայի այս հատկությունը հայտնի է Պաուլիի արգելման սկզբունք անունով:

N փոխազդող մասնիկների համար ալիքային ֆունկցիան ֆունկցիա է բոլոր մասնիկների կոօրդինատներից և ժամանակից և չի կարող տարանջատվել առանձին մասնիկների ալիքային ֆունկցիաների: Այնուամենայնիվ, չփոխազդող մասնիկների համար ժամանակից անկախ պոտենցիալի եդպքում ալիքային փունկցիան կարելի է ներկայացնել մասնիկների առանձին ալիքային ֆունկցիաների արտադրյալի տեսքով՝

$\Psi = \phi(t)\prod_{i=1}^N\psi(\bold{r}_i) = \phi(t)\psi(\bold{r}_1)\psi(\bold{r}_2)\cdots\psi(\bold{r}_N).$

Սպին ունեցող մեկ մասնիկը եռաչափ դեպքում

1/2 սպին ունեցող մասնիկի ալիքային ֆունկցիան միաչափ դեպքում: Պայմանականորեն պատկերված է սպինի ուղղությունը: Իրականում մասնիկները չեն պտտվում իրենց առանցքի շուրջը:

Սպին ունեցող մասնիկի համար ալիքային ֆունկցիան կարող է գրվել «սպինային կոօրդինատային տարածությունում»՝

$\Psi(\mathbf{r},s_z,t)$

s_z-ը սպինի պրոյեկցիայի քվանտային թիվն է կամայականորեն ընտրված z առանցքով:Ի տարբերություն r-ի և t-ի, s_z պարամետրը դիսկրետ փոփոխական է: Օրինակ, ½ սպինով մասնիկի համար s_z-ը կարող է լինել միայն +1/2 կամ -1/2 (Ընդհանուր դեպքում, s սպինի համար s_z-ը կարող է լինել s, s–1,...,–s:): Եթե մասնիկի դիրքը և սպինը միաժամանակ են չափվում t պահին, հավանականությունը, որ այն R₁ մեկ տիրույթում է և սպինի պրոյեկցիայի քվանտային թիվը m է՝

$P_{\mathbf{r}\in R,s_z=m} = \int\limits_{R} \mathrm{d}^3\mathbf{r} |\Psi(\mathbf{r},t,m)|^2$

Նորմավորման պայմանը՝

$\sum_{\mathrm{all\, }s_z} \int\limits_{{\rm all \, space}} |\Psi(\mathbf{r},t,s_z)|^2 \mathrm{d}^3\mathbf{r} = 1$;

Քանի որ սպինային քվանտային թիվը դիսկրետ արժեքներ է ընդունում, այս պայմանը պետք է գրվի որպես բոլոր արժեքների գումար, ոչ թե ինտեգրալ:

Սպին ունեցող բազմաթիվ մասնիկները եռաչափ դեպքում

Համանման ձևով, սպին ունեցող N մասնիկների ալիքային ֆունկցիան՝

$\Psi(\mathbf{r}_1, \mathbf{r}_2 \cdots \mathbf{r}_N, s_{z\,1}, s_{z\,2} \cdots s_{z\,N}, t)$:

Հավանականությունը, s_z1 = m₁ սպինով 1 մասնիկը կգտնվի R₁ տիրույթում և s_z2 = m₂ սպինով 2 մասնիկը կգտնվի R₂ տիրույթում և այլն՝

$P = \int\limits_{R_1} \mathrm{d}^3\mathbf{r}_1 \int\limits_{R_2} \mathrm{d}^3\mathbf{r}_2\cdots \int\limits_{R_N} \mathrm{d}^3\mathbf{r}_N \left | \Psi\left (\mathbf{r}_1 \cdots \mathbf{r}_N,m_1\cdots m_N,t \right ) \right |^2$

Նորմավորման պայմանը՝

$\sum_{s_{z\,N}} \cdots \sum_{s_{z\,2}} \sum_{s_{z\,1}} \int\limits_{{\rm all \, space}} \mathrm{d}^3\mathbf{r}_1 \int\limits_{{\rm all \, space}} \mathrm{d}^3\mathbf{r}_2\cdots \int\limits_{{\rm all \, space}} \mathrm{d}^3 \mathbf{r}_N \left | \Psi \left (\mathbf{r}_1 \cdots \mathbf{r}_N,s_{z\,1}\cdots s_{z\,N},t \right ) \right |^2 = 1$

Չփոխազդող մասնիկների համար ժամանակից անկախ պոտենցիալի դեպքում ալիքային ֆունկցիան առանձին մասնիկների ալիքային ֆունկցիաների արտադրյալն է՝

$\Psi = \phi(t)\prod_{i=1}^N\psi(\bold{r}_i,s_{z\,i}) = \phi(t)\psi(\bold{r}_1,s_{z\,1})\psi(\bold{r}_2,s_{z\,2})\cdots\psi(\bold{r}_N,s_{z\,N}).$

Տե՛ս նաև

• Բոզոն
• Ֆերմիոն

Հղումներ

2.Quantum Mechanics(Non-Relativistic Theory), L.D. Landau and E.M. Lifshitz, ISBN 0-08-020940-8