Լագրանժի կետ

Լագրանժի կետ, լիբերացիայի կետ (լատին․՝ librātiō - ճոճում) կամ L-կետ, երկու մեծ զանգված ունեցող մարմինների համակարգում կետ, որում երրորդ մարմինը կարող է մնալ անշարժ այս մարմինների նկատմամբ, ունենալով անհամեմատելի փոքր զանգված, որի վրա չեն ազդում այլ ուժեր բացի առաջին երկու մարմինների ձգողական ուժերից։
Առավել ճշգրիտ Լագրանժի կետերը իրենցից ներկայացնում են երեք մարմնի խնդրի մասնավոր դեպք, երբ բոլոր արմինների ուղեծրերը հանդիսանում են շրջանաձև և նրանցից մեկի զանգվածը շատ անգամ փոքր է մյուս երկուսինից։ Այս դեպքում կարելի է համարել, որ երկու զանգվածեղ մարմինները պտտվում են իրենց ընդհանուր ծանրության կենտրոնի շուրջ հաստատուն անկյունային արագությամբ։ Տարածության մեջ նրանց շուրջ կան հինգ կետեր, որտեղ գտնվելու դեպքում երրորդ մարմինը, ունենալով անհամեմատելի փոքր զանգված, կարող է մնալ անշարժ պտտվող հաշվարկի համակարգում, կապված մեծ մարմինների հետ։ Այս կետերում փոքր մարմնի վրա ազդող ձգողականության ուժերը հավասարակշռվում են կենտրոնախույս ուժով։
Լագրանժի կետերը ստացել են իրենց անունը մաթեմատիկոս Ժոզեֆ Լագրանժի պատվին, ով առաջինն է հայտնաբերել այս երևույթը 1772 թվականին։
Լագրանժի կետերի տեղաբաշխումը[խմբագրել | խմբագրել կոդը]
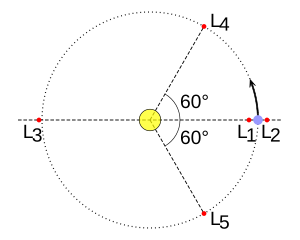
Բոլոր Լագրանժի կետերը ընկնում են զանգվածեղ մարմինների ուղեծրային հարթություններում և նշանակվում են լատինական մեծատառ L տառով, թվային 1 - 5 ինդեքսով՝
- L1 գտնվում է երկու մարմինների միջև, ավելի փոքր մարմնին ավելի մոտ,
- L2 գտնվում է դրսում, ավելի փոքր մարմնի ետևում
- L3 գտնվում է փոքր մարմնի հակառակ ուղղությամբ մեծ մարմնի ետևում։
Այս երեք կետերը անվանում են նաև համագծային, քանի որ նրանք գտնվում են մեկ ուղիղի վրա։
Համակարգի ծանրության կենտրոնից մինչև այդ կետերը հաշվարկվում է հետևյալ բանաձևերով[1][2]։
որտեղ՝ ,
- R — մարմինների միջև հեռավորությունն է,
- M1 — ավելի ծանր մարմնի զանգվածը,
- M2 — երկրորդ մարմնի զանգվածը։
L1[խմբագրել | խմբագրել կոդը]
L1 կետը ընկած է M1 և M2 (M1 զանգվածը > M2-ից) մարմինները միացնող գծի վրա և գտնվում է նրանց միջև, երկրորդ մարմնին մոտ։ Նրա առկայությունը պայմանավորված է նրանով, որ M2 մարմնի ձգողությունը մասնակիորեն կոմպենսացնում է M1 մարմնի ձգողության ուժը։ Ընդ որում, որքանով մեծ է M2 մարմինը, այնքան հեռու կլինի այդ կետը երկրորդ մարմնից։
- Օրինակ՝ Մարմինները, որոնք շարժվում են Արեգակի շուրջ ավելի մոտ քան Երկիրը, որպես կանոն, ունեն ավելի փոքր ուղեծրային պարբերություն քան Երկրինն է, եթե նրանք չեն մտնում Երկրի ձգողության դաշտի ազդեցության ոլորտը։ Եթե մարմինը գտնվում է անմիջականորեն Երկրի և Արեգակի միջև, ապա Երկրի ձգողության ուժը մասնակիորեն կոմպենսացնում է Արեգակի ձգողության ազդեցությունը, դրա հաշվին տեղի է ունենում մարմնի ուղեծրային պարբերության ավելացում։ Ընդ որում, որքանով մոտ է այդ մարմինը Երկրին, այնքան մեծ է այդ էֆեկտը։ Ի վերջո, որոշակի հեռավորության վրա մոլորակից L1 կետում, Երկրի ձգողության ուժը հավասարակշռում է արեգակնային ձգողության ուժը, այնպես, որ մարմնի պտույտի պարբերությունը դառնում է հավասար Երկրի պտույտի պարբերությանը։ Մեր մոլորակի համար L1 կետի հեռավորությունը կազմում է 1, 5 միլիոն կմ։ Այստեղ Արեգակի ձգողությունը 2 %-ով (118 մկմ/վ2) ավելի ուժեղ է, քան Երկրի ուղեծրում (5, 9 մմ/վ2), այն դեպքում երբ անհրաժեշտ կենտրոնախույզ ուժի նվազեցումը երկու անգամ փոքր է (59 մկմ/վ2): Այս երկու էֆեկտների գումարը հավասարակշռվում է Երկրի ձգողությամբ, որը կազմում է այստեղ 177 մկմ/վ2։
Արեգակ-Երկիր համակարգում L1 կետը կարող է լինել իդեալական վայր Արեգակի դիտարկումներ կատարող աստղադիտակի համար, որը այս կետում երբեք չի ծածկվի Երկրի կամ Լուսնի կողմից։ Օրինակ՝ Արեգակնային հելիոսֆերային աստղադիտարան (SOHO) շարժվում է հալո ուղեծրով L1 կետի շուրջ, երկու այլ սարքերի հետ միասին՝ Advanced Composition Explorer և WIND։
Երկիր-Լուսին համակարգի L1 կետը կարող է լինել իդեալական վայր մարդաբնակ ուղեծրակայան տեղակայելու համար, որը լինելով Երկրից Լուսին ճանապարհի «կեսին» թույլ կտար հեշտությամբ հասնել Լուսնին ծախսելով նվազագույն վառելիք և կարող է դառնալ կարևոր կետ Երկրից Լուսին բեռնափոխադրումներ իրականացնելու համար։
L2[խմբագրել | խմբագրել կոդը]
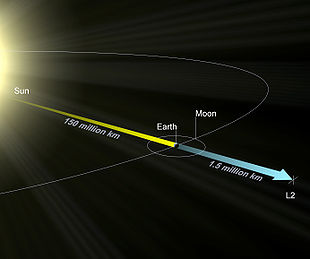
L2 կետը ընկած է M1 և M2 (M1 զանգվածը > M2-ից) մարմինները միցնող գծի վրա, և գտնվում է փոքր զանգվածով մարմնից դուրս։ L1 և L2 կետերը տեղակայված են նույն գծի վրա M1 >> M2 միջակայքում և սիմետրիկ են M2-ի նկատմամբ։ L2 կետում մարմնի վրա ազդող ձգողության ուժերը կոմպենսացնում են կենտրոնախույզ ուժերի ազդեցությունը պտտվող հաշվման համակարգում։
- Օրինակ՝ Երկրի ուղեծրից դուրս շարժվող մարմինների ուղեծրային պարբերությունը համարյա միշտ մեծ է քան Երկրինը։ Սակայն մարմնի վրա Երկրի ձգողության ուժի ավելցուկային ազդեցությունը, Արեգակի ձգողության ուժից զատ, բերում է պտույտի արագության ավելացմանը և Արեգակի շուրջ պտույտի ժամանակի նվազմանը, արդյունքում, L2 կետում ուղեծրի պտույտի պարբերությունը դառնում է հավասար Երկրի պտույտի պարբերությանը։
Արեգակ-Երկիր համակարգում L2 կետը իդեալական վայր է հանդիսանում ուղեծրային տիեզերական աստղադիտարանների կառուցման համար։ Քանի որ, մարմինը L2 կետում կարող է երկար ժամանակ պահպանել իր ուղղվածությունը Արեգակի և Երկրի հանդեպ, նրա էկրանավորումը և չափաբերումը դառնում է անհամեմատ ավելի հեշտ։ Սակայն, այս կետը տեղակայված է մի փոքր ավելի հեռու Երկրի շողքից (կիսաշողքի տարածքում)[3], այնպես, որ արեգակնային ռադիացիան ամբողջությամբ չի կասեցվում։ Այս կետում արդեն գտնվում են ամերիկյան և եվրոպական տիեզերական գործակալությունների սարքերը WMAP, Պլանկ և տիեզերական աստղադիտակ Հերշելը։ 2012 թվականին նրանց կարող է միանալ Գայա աստղադիտակը, իսկ 2018-ին՝ Ջեյմս Վեբբը։ Երկիր Լուսին համակարգի L2 կետը կարող է օգտագործվել Լուսնի չերևացող մասում գտնվող օբյեկտների հետ կապ պահպանելու համար, ինչպես նաև կարող է լինել հարմար տող, տեղադրելու համար վառելիքի լցակայան Երկիր - Լուսին բեռնափոխադրման համար[4]
Եթե M2 մարմինը շատ անգամ փոքր է M1-ից զանգվածով, ապա L1 և L2 կետերը գտնվում են մոտավորապես նույն r հեռավորության վրա M2 մարմնից, որը հավասար է Հիլի գնդի շառավղին՝
որտեղ՝ R - հեռավորությունն է համակարգի բաղկացուցիչ մասերի միջև։
Այս հեռավորությունը կարելի է բնութագրել, որպես M2-ի շուրջ շրջանաձև ուղեծրի շառավիղ, որի համար պտույտի պարբերությունը M1-ի բացակայության դեպքում կլիներ անգամ փոքր, քան M2 պտույտի պարբերությունն է M1-ի շուրջ։
Օրինակներ[խմբագրել | խմբագրել կոդը]
- Արեգակ - Երկիր համակարգում՝ 1 500 000 կմ հեռավորության վրա Երկրից
- Երկիր - Լուսին համակարգում՝ 61 500 կմ հեռավորության վրա Լուսնից
L3[խմբագրել | խմբագրել կոդը]

L3 կետը ընկած է M1 և M2 (M1 զանգվածը > M2-ից) մարմինները միցնող գծի վրա, և գտնվում է մեծ զանգվածով մարմնից դուրս։ Ինչպես և L2 կետում, այս կետում էլ ձգողության ուժերը հավասարակշռում են կենտրոնախույզ ուժերը։
- Օրինակ՝ Արեգակ-Երկիր համակարգի L3 կետը գտնվում է Արեգակից այն կողմ, Երկրից հակառակ ուղղությամբ։ Չնայած իր աննշան, Արեգակի հետ համեմատ, ձգողության ուժի մեծության այս կետում, Երկիրը միևնույն է ազդում է այս կետի վրա, այդ պատճառով L3 կետը գտնվում է ոչ թե Երկրի ուղեծրի վրա, այլ մի փոքր ավելի մոտ Արեգակին։ Արդյունքում, L3 կետում գործում է Արեգակի և Երկրի ձգողության ուժերի այնպիսի համադրություն, որ այստեղ գտնվող մարմինները շարժվում են այնպիսի պտույտի պարբերությամբ, ինչպիսին Երկրինն է։
Մինչ տիեզերագնացության ժամանակաշրջանը ֆանտաստ գրողների միջև շատ տարածված էր այն գաղափարը, որ Երկրի հակադարձ կողմում, L3 կետում, կա մի այլ մոլորակ, որը անվանում էին «Հակաերկիր», որը իր տեղադրության պատճառով անհասանելի էր ուղիղ դիտարկումների համար։ Սակայն, տիեզերական սարքերով դիտարկումներ կատարելու հնարավորությունը ցույց տվեց, որ այս տեսությունը սխալ է։ Իրականում այլ մոլորակների ձգողականության ազդեցության պատճառով Արեգակ - Երկիր համակարգի L3 կետը հանդիսանում է չափազանց անկայուն։ Այսպես, Երկրի և Վեներայի առճակատման ժամանակ, որը տեղի է ունենում ամեն 20 ամիսը մեկ, վերջինս գտնվում է ընդամենը 0, 3 ա. մ. հեռավորության վրա L3 կետից և այդպիսով ունենում է չափազանց լուրջ ազդեցություն այս կետի տեղադրության վրա։ Բացի դրանից, Երկրի հանդեպ Արեգակ - Յուպիտեր համակարգի ծանրության կենտրոնի չհավասարակշռվածության և Երկրի ուղեծրի էլիպտիկության պատճառով, այսպես կոչված Հակաերկիրը միևնույն է, ժամանակ առ ժամանակ, հասանելի կլիներ դիտարկումների համար և արդեն հայտնաբերված կլիներ։
L3 կետի մոտակայքում տեղակայված տիեզերական սարքերը կարող են անընդհատ հետևել և հաղորդել տարբեր ակտիվության ձևերի մասին Արեգակի մակերևույթի վրա, մասնավորապես, նոր պետերի կամ փայլատակումների մասին, և կարող է օգտագործվել որպես տիեզերական եղանակի մասին վաղ նախազգուշացման համակարգ 7 օր ժամանակահատվածով։ Բացի այդ, այսպիսի արբանյակներից ստացված տեղեկատվությունը կարող է օգտագործվել մարդկանց հեռահար տիեզերական թռիչքների անվտանգության ապահովելու համար, օրինակ դեպի Մարսը կամ աստերոիդները։ 2010 թվականին դիտարկվում էին մի քանի տարբերակներ այսպիսի սարքի արձակման համար[5]
L4 և L5[խմբագրել | խմբագրել կոդը]

Եթե համակարգի երկու մարմինները միացնող գծի հիման վրա կառուցել երկու հավասարակողմ եռանկյուն, որի երկու գագաթները գտնվում են M1 և M2 մարմինների կենտրոններին, ապա L4 և L5 կետերը կհամապատասխանեն այս եռանկյունների երրորդ գագաթներին, տեղադրված երկրորդ մարմնի ուղեծրի հարթությունում, 60 °-ով մարմնից առաջ և ետ։
Այս կետերի գոյությունը և նրանց կայունությունը պայմանավորված է այն հանգամանքով, որ այս կետերում, որոնք գտնվում են երկու մարմիններից հավասար հեռավորության վրա, երկու զանգվածեղ մարմինների ձգողության ուժերը հարաբերվում են նույն հարաբերությամբ ինչպես և նրանց զանգվածները, և այսպիսով, արդյունքային ուժը ուղղված է համակարգի բարիկենտրոնին։ Բացի այդ, ուժերի եռանկյան երկրաչափությունը հաստատում է, որ արդյունքային արագացումը կապված է բարիկենտրոնից հեռավորության հետ նույն հարավերությամբ, ինչպես երկու զանգվածեղ մարմինների համար։ Քանի որ, բարիկենտրոնը հանդիսանում է համակարգի միաժամանակ և ծանրության կենտրոնը և պտույտի կենտրոնը, արդյունքային ուժը ճշգրիտ համապատասխանում է այն ուժին, որը անհրաժեշտ է մարմնի պահպանման համար Լագրանժի կետում, ուղեծրային հավասարակշռության մեջ համակարգի հետ (իրականում, երրորդ մարմնի զանգվածը չպետք է լինի աննշան փոքր)։ Այս եռանկյունի դասավորությունը հայտնաբերվել է Լագրանժի կողմից երեք մարինների խնդրի վրա աշխատելիս։ L4 և L5 կետերը անվանում են եռանկյունային (ի տարբերություն համագծայիններից)։
Այս կետերը նույնպես անվանում են տրոյական՝ այս անվանումը ծագում է Յուպիտերի տրոյացի աստերոիդներից, որոնք հանդիսանում են այս կետերի ամենավառ արտահայտությունը։ Նրանք անվանվել էին Տրոյական պատերազմի հերոսների պատվին Հոմերոսի «Իլիական» ստեղծագործությունից, ընդ որում L4 կետում գտնվող աստերոիդները ստանում են հույների անուններ, իսկ L5 կետինները Տրոյայի պաշտպաններինը, այս պատճառով ել նրանց խմբերը անվանում են «հույներ» և «տրոյացիներ»։
Համակարգի ծանրության կենտրոնից մինչև այս կետերը ընկած հեռավորությունը, կոորդինատային համակարգում, որի կենտրոնը գտնվում է ծանրության կենտրոնում, հաշվարկվում է հետևյալ բանաձևերով՝
որտեղ՝
- ,
- R — մարմինների միջև հեռավորությունը,
- M1 — ավելի ծանր մարմնի զանգվածը,
- M2 — Երկրորդ մարմնի զանգվածը։
Օրինակներ[խմբագրել | խմբագրել կոդը]
- 2011 թվականին Արեգակ - Երկիր համակարգի L4 տրոյական կետում հայտնաբերվել է աստերոիդ[6]։ L5 կետում դեռևս տրոյացի աստերոիդներ չեն հայտնաբերվել, բայց այնտեղ դիտարկվում է բավականին մեծ տիեզերական փոշու կուտակում։
- Որոշ դիտարկումների համաձայն, Երկիր - Լուսին համակարգի L4 և L5 կետերում գտնվում են չափազանց նոսր միջմոլորակային փոշու կուտակումներ՝ Կորդիլևսկու ամպեր։
- Արեգակ - Յուպիտեր համակարգում L4 և L5 կետերի մոտակայքում գտնվում են այսպես կոչված Յուպիտերի տրոյացի աստերոիդները։ 2010 թվականի հոկտեմբերի 21-ի տվյալներով հայտնի են մոտ չորս և կես հազար այսպիսի աստերոիդներ[7]։
- Տրոյացի աստերոիդներ կան ոչ միայն Յուպիտերի L4 և L5 կետերում, բայց նաև Նեպտունի մոտ[8].
- Այլ հետաքրքիր օրինակ է հանդիսանում Սատուրնի արբանյակ Տեֆիյան, որի L4 և L5 կետերում գտնվում են երկու փոքր արբանյակներ՝ Տելեստոն և Կալիպսոն։ Եվս մեկ զույգ արբանյակներ Սատուրն - Դիոնա համակարգում գտնվում են՝ Ելենան L4 կետում և Պոլիդեվկը L5 կետում։ Տեֆիյան և Դիոնան հարյուրավոր անգամներ ավելի զանգվածեղ են իրենց «ուղեկցորդներից», և չափազանց թեթևեն Սատուրնից, որը կայուն է դարձնում այս համակարգը։
- Հսկայական բախման տեսության սցենարներից մեկը ենթադրում է, որ ենթադրական պրոտոմոլորակ (պլանետեզեմալ) Տեյան, որի հետ Երկրի բախման արդյունքում առաջացել է Լուսինը, ձևավորվել է Արեգակ - Երկիր համակարգի Լագրանժի L4 կամ L5 կետերում[9].
- KOI-730 համակարգում չորս մոլորակներից երկուսը պտտվում են իրենց արևի շուրջ նույն ուղեծրով։ այս երկու մարմինը միշտ բաժանում է 60 աստիճան հեռավորություն[10]։
Հավասարակշռությունը Լագրանժի կետերում[խմբագրել | խմբագրել կոդը]

Համագծային Լագրանժի կետերում տեղակայված մարմինները գտնվում են անկայուն հավասարակշռության մեջ։ Օրինակ, եթե L1 կետում գտնվող մարմինը թեթևակի շարժվում է երկու զանգվածեղ մարմինները միացնող գծի երկայնքով, ապա այն մարմնի ձգողության ուժը, որին մարմինը մոտենում է աճում է, իսկ մյուսինը նվազում։ Արդյունքում մարմինը ավելի ու ավելի է հեռանում հավասարակշռության դիրքից։
Մարմինների այսպիսի պահվածքը L1 կետի մոտակայքում կարևոր դեր է խաղում մոտ կրկնակի աստղերի համակարգերում։ Ռոշի խորշերը այսպիսի համակարգերում իրար կպնում են L1 կետում, այդ պատճառով, երբ զույգ աստղերից մեկը էվոլյուցիայի ընթացքում լցնում է Ռոշի խորշը, մատերիան հոսում է դեպի մյուս աստղը հենց Լագրանժի L1 կետով[11]։
Չնայած այս ամենին, համաուղեծիր կետերի շուրջ գոյություն ունեն կայուն փակ ուղեծրեր (պտտվող կոորդինատային համակարգում), առնվազն երեք մարմնի խնդրի դեպքում։ Եթե շարժման վրա ազդում են նաև այլ մարմիններ (ինչպես դա տեղի է ունենում Արեգակնային համակարգում), ապա փակ ուղեծրի փոխարեն մարմինը կշարժվի կեղծ-պարբերական ուղեծրով, որոնք ունեն Լիսաժուի կորերի ձև։ Չնայած այսպիսի ուղեծրի անկայունությանը տիեզերական սարքը կարող է մնալ այս ուղեծրի վրա երկար ժամանակահատվածում, ծախսելով հարաբերականորեն քիչ վառելիք[12]։
Ի տարբերություն համագծային լիբերացիայի կետերի, տրոյական կետերում ապահովվում է կայուն հավասարակշռություն, եթե M1/M2 > 24, 96։ Մարմնի շեղման դեպքում ծագում են Կորիոլիսի ուժեր, որոնք շեղում են ուղեծիրը և մարմինը շարժվում է լիբերացիայի կետի շուրջ[1].
Գործնական օգտագործումը[խմբագրել | խմբագրել կոդը]
Տիեզերագնացության ոլորտի հետազոտողները վաղուց արդեն ուշադրություն են դարձրել Լագրանժի կետերի վրա։ Օրինակ, Արեգակ - Երկիր համակարգի L1 կետում հարմար է տեղակայել տիեզերական արևային աստղադիտարան, այն երբեք չի հայտնվի Երկրի շողքում, և հետևաբար կարող է կատարել անընդհատ դիտարկումներ։ L2 կետը հարմար է տիեզերական աստղադիտակի համար, այստեղ Երկիրը համարյա ամբողջությամբ ծածկում է Արեգակի լույսը, և ինքն էլ չի խանգարում դիտարկումներին, քանի որ շրջված է դեպի այդ կետը չլուսավորված կողմով։ Երկիր - Լուսին համակարգի L1 կետում հարմար կլինի տեղադրել հաղորդիչ կայան Լուսնի բնակեցման ընթացքում։ Այն միշտ կմնա Լուսնի համարյա ամբողջ Երկրին ուղղված կողմի համար տեսանելի գոտում, և կապը ապահովելու համար պետք կլինեն հազարավոր անգամ ավելի ցածր հզորությամբ կայաններ, քան Երկրից կապի ապահովման դեպքում։
Այս պահին մի քանի տիեզերական սարքեր, առաջին հերթին աստղաֆիզիկական աստղադիտակներ, տեղակայված են Արեգակնային համակարգի տարբեր Լագրանժի կետերում[12]՝
- SOHO (անգլ.՝ Solar and Heliospheric Observatory, «Արևային և հելիոսֆերային աստղադիտարան») գտնվում է Արեգակի և Երկրի միջև L1 կետում։
- WMAP (անգլ.՝ Wilkinson Microwave Anisotropy Probe, «Ուիլկինսոնի միկրոալիքային անիզոտրոպ սարք»), ուր ուսումնասիրում է ռելիկտային ճառագայթումը, գտնվում է Երկրիուղեծրից դուրս L2 կետում։
- Advanced Composition Explorer, գտնվում է Արեգակ - Երկիր համակարգի L1 կետում[13]։
- Երկու STEREO սարք, 2009 թվականի սեպտեմբեր-հոկտեմբեր ամիսներին կատարեցին անցում L4 և L5 կետերով[14]։
- «Հերշել» և «Պլանկ» աստղադիտակները, որոնք արձակվել էին 2009 թվականի մայիսի 14-ին, գտնվում են Արեգակ - Երկիր համակարգի L2 կետում[15][16]։
- Ջեյմս Վեբբ տիեզերական աստղադիտակը, որը կփոխարինի Հաբլին, նախատեսված է տեղակայել Արեգակ - Երկիր համակարգի L2 կետում։ Արձակումը նախատեսվում է 2018 թվականին[17]։
- JIMO (անգլ.՝ Jupiter Icy Moons Orbiter, Յուպիտորի սառցե արբանյակների ուզեծրակայան), Յուպիտերի արբանյակների ուսումնասիրման ծրագիրը, որը նախատեսվում էր իրականացնել 2017 թվականին ՆԱՍԱ-ի կողմից, սակայն ֆինանսական միջոցների սղության պատճառով փակվել է 2005 թվականին, պետք է ակտիվորեն օգտագործեր Լագրանժի կետերի համակարգը մի արբանյակից մյուսը անցման ժամանակ ուղեծրը փոխելիս, վառելիքի խնայողությամբ։ Այս մանևրը ստացել է «Լագրանժի աստիճան» անվանումը[18]։
- WIND տիեզերական սարքը, որը նախատեսվում էր Արեգակնային քամու ուսումնասիրության համար։ Արձակվել է 1994 թվականին և այս պահին գտնվում է L1 կետում։
Հիշատակումները մշակույթում[խմբագրել | խմբագրել կոդը]
Լագրանժի կետերը բավականին տարածված են տիեզերքի հետազոտությունների մասին գիտաֆանտաստիկական ստեղծագործություններում։ Հեղինակները հաճախ այդ կետերում են տեղադրում բնակելի կամ ավտոմատ կայաններ, տես օրինակ՝ Հարի Հարիսոնի «Վերադարձ դեպի աստղերը», Վերնոր Վինջի «Խորություն երկնքում», Բաբելոն-5 հեռուստասերիալ։
Երբեմն Լագրանժի կետերում են տեղադրում նաև ավելի հետաքրքիր մարմիններ՝ աղբանոցներ (Չարլզ Շեֆիլդի «Մտքերի միավորումը», և Անդրեյ Բալաբուխայի «Նեպտունի քնարը»), այլմոլորակայինների արտեֆակտներ (Լարրի Նիվենի «Պաշտպանը») կամ նույնիսկ ամբողջական մոլորակներ (Պոլ Անդերսոնի «Մոլորակը, որտեղից չեն վերադառնում»)։ Այզեկ Ազիմովը առաջարկում էր ուղարկել Լագրանժի կետեր ռադիոակտիվ թափոնները («Տեսարան բարձունքից»)։
Տես նաև[խմբագրել | խմբագրել կոդը]
- Տրոյացիներ
- Տրոյացի աստերոիդների ցանկ («տրոյացիներ»)
- Տրոյացի աստերոիդների ցանկ («հույներ»)
- Տրոյացի արբանյակներ
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ 1,0 1,1 «Լագրանժի կետերի տեղադրության հաշվարկ» (PDF). Արխիվացված է օրիգինալից (PDF) 2015 թ․ սեպտեմբերի 7-ին. Վերցված է 2012 թ․ հունիսի 24-ին.
- ↑ «L4 և L5 կետերի տեղադրության հաշվարկ». Արխիվացված է օրիգինալից 2012 թ․ մայիսի 5-ին. Վերցված է 2012 թ․ հունիսի 24-ին.
- ↑ Արեգակի անկյունային չափը 1 ա. մ. + 1500000 կմ հեռավորության վրա՝ 31, 6', Երկրի անկյունային չափը 1500000 կմ մղոնի վրա՝ 29, 3'
- ↑ Զելգեր, Ֆրանկ; Բերնարդ Կատլեր (2010 թ․ սեպտեմբերի 2). «Անցում պահեստավորման կայանների վրա հիմնված տիեզերական բեռնափոխադրմանը» (PDF). AIAA SPACE 2010 Conference & Exposition. AIAA. էջ 4. Արխիվացված է օրիգինալից (PDF) 2011 թ․ օգոստոսի 24-ին. Վերցված է 2011 թ․ հունվարի 25-ին. «L2 կետը գտնվում է տիեզերքում բավականին հեռու մոլորակի մակերևույթից և հետևաբար ջերմային, միկրոերկնաքարային և ատմիկ թթվածնային միջավայրերից, որոնք առկա են ցածր երկրիկ ուղեծրերում։ Ջերմադինամիկ կայունությունը և սարքավորումների պահպանումը շատ ավելի հեշտ է ապահովել այստեղ, քան ցածր երկրիկ ուղեծրերում։ L2 կետը ոչ միայն հիանալի միջանկյալ կայան է, դա հիանալի տեղ է պահելու այրվող նյութերը։ ... L2 կետը իդեալական տեղ է վառելիք և տիեզերանավեր պահելու համար՝ այն մոտ է, բարձր էներգիա է պարունակում և այնտեղ ցուրտ է։»
- ↑ Տանդարինի, Մարկո; Ֆանտինո, Ելենա; Խուան Ռեն, Պերիպաոլո Պերգոլա, Ջերարդ Գիմեզ և Ջոզեպ Մասդերմոնտ (2010). «Տիեզերանավերի հետագծերը դեպի Արեգակ - Երկիր համակարգի L3 կետը». Երկնային մեխանիկա և դինամիկ աստղագիտություն (Սպրինգեր).
{{cite journal}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link)(չաշխատող հղում) - ↑ Աստղագետները հայտնաբերել են Երկրի առաջին տրոյացի արբանյակը
- ↑ Յուպիտերի տրոյացիների ցանկ
- ↑ «Նեպտունի տրոյացիների ցանկ». Փոքր մոլորակների կենտրոն. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 24-ին. Վերցված է 2010 թ․ հոկտեմբերի 27-ին.
- ↑ Ի. Բելբրունո; Ռիչարդ Գոտտ III (2005)՝ «Որտեղից է առաջացել Լուսինը». Աստղագիտական ամսագիր 129 (3)։ 1724—1745. arXiv: astro-ph/0405372
- ↑ «Առաջին անգամ գտնվել են երկու մոլորակներ մեկ ուղեծրի վրա». Արխիվացված է օրիգինալից 2013 թ․ հուլիսի 25-ին. Վերցված է 2012 թ․ հունիսի 24-ին.
- ↑ Աստրենետ. Մոտ կրկնակի աստղերը իրենց էվոլյուցիայի ուշ փուլերում
- ↑ 12,0 12,1 WMAP Աստղադիտարան - Լագրանժի կետեր (ՆԱՍԱ)
- ↑ ACE Ծրագրի նկարագիրը
- ↑ Space.com: Արեգակնային համակարգի կորսված մոլորակի որոնումները
- ↑ Lenta.ru-ն «Հերշել» աստղադիտակի մասին
- ↑ ««Պլանկ» տիեզերական աստղադիտակը դարձավ ամենասառը մարմինը տիեզերքում». Lenta.ru. 2009 թ․ հուլիսի 6. Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 24-ին. Վերցված է 2010 թ․ օգոստոսի 14–ին-ին.
- ↑ Ջեյմս Վեբբ աստղադիտակը (ՆԱՍԱ)
- ↑ Ալեքսանդր Սերգեև «Լագրանժի աստիճան» (ներդիր Իգոր Աֆանասևի և Դմիտրի Վորոնցովի հոդվածի մեջ՝ «Միջմոլորակային աճպարարություն»), «Վոկրուգ Սվետա», №8 (2815) 2008:
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- Լագրանժի կետեր (անգլ.)
- Լագրանժի կետերը գիտական ֆանտաստիկայում Արխիվացված 2009-06-29 Wayback Machine(ռուս.)
| ||||||||||||||||||||||||||||||
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի՝ {{{1}}} թվականի {{{2}}} շաբաթվա հոդված։ |

![{\displaystyle r_{1}=\left(R\left[1-\left({\frac {\alpha }{3}}\right)^{1/3}\right],0\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f622f61df8034654941f89e639abe43f453b1bbc)
![{\displaystyle r_{2}=\left(R\left[1+\left({\frac {\alpha }{3}}\right)^{1/3}\right],0\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d9755e04cc5d6ad636d227264b14cc3ce2b9e61)
![{\displaystyle r_{3}=\left(R\left[1+{\frac {5}{12}}\alpha \right],0\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbd9e92022f983ea210c4dd6c9b8bef16283299b)

![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)
















