Եռանկյունների լուծում
Եռանկյունների լուծում (լատին․՝ solutio triangulorum), պատմական տերմին, որով նշանակվում է եռանկյունաչափության գլխավոր խնդրի լուծումը՝ եռանկյան հայտնի տվյալներով (կողմեր, անկյուններ և այլն) գտնել նրա մյուս տվյալները[1]։ Գոյություն ունեն նաև խնդրի ընդհանրացումներ այն դեպքում, երբ տրված են եռանկյան մյուս տարրերը (օրինակ՝ միջնագծերը, կիսորդները, բարձրությունները, եռանկյան մակերեսը և այլն)։ Եռանկյունը կարող է գտնվել հարթության կամ գնդային մակերևույթի վրա։ Տվյալ խնդիրը հաճախ հանդիպում է եռանկյունաչափությունը կիրառելիս, օրինակ՝ գեոդեզիայի, աստղագիտության, ճարտարապետության, նավագնացության մեջ։
Հարթ եռանկյունների լուծումներ[խմբագրել | խմբագրել կոդը]

Ընդհանուր դեպքում եռանկյունն ունի 6 հիմնական բնութագիր՝ 3 գծային (կողմերի երկարությունները՝ ), և 3 անկյունային ()։ Կողմը, որը ընկած է գագաթի անկյան դիմաց, ընդունված է նշանակել նույն տառով, ինչով որ նշանակված է տվյալ գագաթը, բայց փոքրատառ։ Հարթաչափության դասական խնդրում տրվում են այս 6 բնութագիրներից 3-ը, և պահանջվում է գտնել մյուս 3-ը։ Ակնհայտ է, որ եթե հայտնի լինեն միայն 2 կամ 3 անկյուն, հնարավոր չի լինի միարժեք լուծում գտնել, քանի որ յուրաքանչյուր եռանկյուն, որը նման է տրվածին, նույնպես կլինի լուծում, այդ պատճառով ենթադրվում է, որ հայտնի մեծություններից գոնե մեկը գծային է[2]։
Խնդրի լուծման ալգորիթմը կախված է խնդրի հայտնի մեծություններից։ Տրված մեծությունները պայմանականորեն նշանակվում են Կ (կողմ) և Ա (անկյուն)։ Քանի որ ԱԱԱ զուգակցումը հանված է դիտարկումից, մնում են 5 տարբերակներ[3].
- Երեք կողմ (ԿԿԿ),
- Երկու կողմ և նրանցով կազմված անկյուն (ԿԱԿ),
- Երկու կողմ և կողմերից մեկին կից անկյուն (ԱԿԿ),
- Կողմ երկու կից անկյուններով (ԱԿԱ),
- Կողմ, դիմացի անկյուն ու կից անկյուններից մեկը (ԱԱԿ)։
Հիմնական թեորեմներ[խմբագրել | խմբագրել կոդը]
Խնդրի լուծման ստանդարտ մեթոդը մի քանի հիմնարար առնչությունների կիրառությամբ է։ Այդ առնչությունների տեղի ունեն բոլոր հարթ եռանկյունների համար[4]։ Դրանք են՝
Դիտողություններ[խմբագրել | խմբագրել կոդը]
- Անհայտ անկյունը գտնելու համար նպատակահարմար է օգտագործել ոչ թե սինուսների, այլ՝ կոսինուսների թեորեմը։ Դրա պատճառն այն է, որ եռանկյան գագաթի անկյան սինուսի արժեքը միարժեքորեն չի որոշում այդ անկյունը[5]։ Օրինակ, եթե ապա անկյունը կարող է լինել և՛ , և՛ , քանի որ այդ անկյունների սինուսները համընկնում են։ Բացառություն է համարվում այն դեպքը, երբ խնդրում նախապես ասվում է, որ տվյալ եռանկյան մեջ բութ անկյուն չի կարող լինել, օրինակ՝ երբ եռանկյունը ուղղանկյուն է։ Կոսինուսի դեպքում այսպիսի խնդիրներ չեն առաջանում, քանի որ -ից ընկած միջակայքում անկյունը կոսինուսի արժեքով միարժեքորեն որոշվում է։
- Եռանկյան կառուցման ժամանակ կարևոր է հիշել, որ կառուցված եռանկյան հայելային արտացոլումը նույնպես խնդրի լուծում է։
- Ենթադրվում է, որ եռանկյունները այլասերված չեն, այսինքն՝ կողմի երկարությունը չի կարող զրո լինել, անկյան չափը՝ -ից փոքր դրական թիվ է։

Երեք կողմեր[խմբագրել | խմբագրել կոդը]
Դիցուք տրված են եռանկյան բոլոր կողմերի արժեքները։ Խնդրի լուծման պարտադիր պայման է, որ տեղի ունենա եռանկյան անհավասարությունը, այսինքն՝ յուրաքանչյուր կողմ փոքր լինի մյուս երկուսի գումարից.
անկյունները գտնելու համար պետք է օգտվել կոսինուսների թեորեմից[6].
Երրորդ անկյունը միանգամից գտնում ենք այն կանոնից, որ բոլոր անկյունների գումարը պետք է լինի 180°.
- :
Խորհուրդ չի տրվում երկրորդ անկյունը հաշվել սինուսների թեորեմով, քանի որ, ինչպես նշված է վերոնշյալ 1 դիտողությունում, հնարավոր է բութ անկյունը շփոթել սուր անկյան հետ։ Այս վտանգը չի առաջանա այն դեպքում, եթե սկզբում ըստ կոսինուսների թեորեմի հաշվենք ամենամեծ կողմի դիմաց ընկած ամենամեծ անկյունը. մյուս երկու անկյունները հաստատ սուր են, հետևաբար դրանց հանդեպ կարելի է կիրառել սինուսների թեորեմը։
Անկյունների հաշվարկի համար օգտագործվում է նաև կոտանգենսների թեորեմը։

Երկու կողմերն ու նրանցով կազմված անկյունը[խմբագրել | խմբագրել կոդը]
Դիցուք տրված են կողմերի երկարություններն ու նրանցով կազմված անկյունը։ Խնդրի այս տարբերակը միշտ ունի միայն մեկ լուծում։ կողմի երկարությունը գտնելու համար նորից կիրառվում է կոսինուսների թեորեմը[7].
Խնդիրը բերվում է նախորդ դեպքին։ Երկրորդ անկյունը գտնելու համար նորից կիրառվում է կոսինուսների թեորեմը.
Երրորդ անկյունը հաշվում են եռանկյան անկյունների մասին թեորեմից. :

Երկու կողմ և նրանցից մեկի դիմաց ընկած անկյուն[խմբագրել | խմբագրել կոդը]
Տվյալ դեպքում կարող է լինել երկու լուծում, միակ լուծում, ընդհանրապես ոչ մի լուծում չլինի։ Դիցուք հայտնի են երկու կողմ՝ և անկյունը։ անկյան հավասարումը կարելի է գտնել սինուսների թեորեմից[8].
Նշանակենք (հավասարման աջ մասը)։ Հնարավոր են հավասարման լուծման 4 դեպքեր[9] [10]:
- Խնդիրը լուծում չունի ( կողմը «չի հասնում» BC կողմի գծին) երկու դեպքում. եթե կամ եթե , ընդ որում :
- Եթե , գոյություն ունի միակ լուծում, ընդ որում եռանկյունը ուղղանկյուն է՝ :
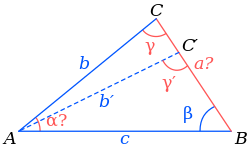
- Եթե , ապա հնարավոր է լուծման երկու տարբերակ։
- Եթե , ապա անկյունը ունի երկու հնարավոր արժեք. սուր անկյուն և բութ անկյուն։
- Եթե , ապա (ինչպես հայտնի է, մեծ կողմին համապատասխանում է հանդիպակաց մեծ անկյուն)։ Քանի որ եռանկյան մեջ չի կարող լինել երկու բութ անկյուն, բութ անկյունը բացառվում է, և լուծումը միակն է։
Երրորդ անկյունը հաշվում են բանաձևով։ Երրորդ կողմը կարելի է նաև գտնել սինուսների թեորեմով.

Կողմը` երկու կից անկյուններով[խմբագրել | խմբագրել կոդը]
Դիցուք տրված է կողմը և երկու անկյունները։ Այս խնդիրն ունի միակ լուծում, եթե երկու անկյունների գումարը փոքր է աստիճանից։ Հակառակ դեպքում խնդիրը լուծում չունի։
Սկզբում որոշվում է 3-րդ անկյունը։ Օրինակ, եթե տրված են անկյունները, ապա : Ապա սինուսների թեորեմով հաշվում են երկու անհայտ կողմերը[11].
- :
Ուղղանկյուն եռանկյունների լուծում[խմբագրել | խմբագրել կոդը]

Այս դեպքում հայտնի է անկյուններից մեկը՝ ուղիղ անկյունը։ Հարկավոր է իմանալ երկու տարրի մեծություն, որոնցից մեկը կողմ է։ Հնարավոր են հետևյալ դեպքերը.
- երկու էջերը,
- էջն ու ներքնաձիգը,
- էջն ու կից սուր անկյունը,
- էջն ու հակադիր սուր անկյունը,
- ներքնաձիգն ու սուր անկյունը։
Ընդունված է ուղիղ անկյան գագաթը նշանակել C տառով, իսկ ներքնաձիգը` : Էջերը նշանակվում են և , իսկ հակադիր անկյունները` համապատասխանաբար α ու β: Հաշվարկամն բանաձևերը էականորեն հեշտանում են, քանի որ սինուսների և կոսինուսների թեորեմնրի փոխարն կարելի է օգտագործել պարզ առնչություններ՝ Պյութագորասի թեորեմը՝
և եռանկյունաչափական ֆունկցիայի հիմնական սահմանումները՝
Պարզ է նաև, որ α և β անկյունները սուր են, քանի որ նրանց գումարը հավասար է : Այդ պատճառով անհայտ անկյուններից յուրաքանչյուրը կարելի է որոշել եռանկյունաչափական որևէ ֆունկցիայի միջոցով (սինուսով, կոսինուսով, տանգենսով և այլն)՝ հաշվելով համապատասխան հակադարձ եռանկյունաչափական ֆունկցիան։ Խնդրի ճիշտ ձևակերպման դեպքում (եթե տրված են էջն ու ներքնաձիգը, ապա էջը պետք է փոքր լինի ներքնաձիգից, իսկ եթե տրված է ոչ ուղիղ անկյուններից մեկը, ապա այն պետք է սուր լինի) միշտ գոյություն ունի լուծում և այն միակն է։
Երկու էջ[խմբագրել | խմբագրել կոդը]
Ներքնաձիգը որոշվում է Պյութագորասի թեորեմով.
Անկյունները կարելի է հաշվել՝ կիրառելով արկտանգենսի ֆունկցիան.
կամ էլ հենց նոր հաշվված ներքնաձիգի միջոցով.
- :
Էջն ու ներքնաձիգը[խմբագրել | խմբագրել կոդը]
Դիցուք հայտնի են էջն ու ներքնաձիգը, այդ դեպքում էջը որոշվում է Պյութագորասի թեորեմով.
- :
Անկյունները հաշվում են նախորդ օրինակի նման։
Էջն ու կից սուր անկյունը[խմբագրել | խմբագրել կոդը]
Դիցուք հայտնի են էջն ու կից α անկյունը։ -ն ներքնաձիգը որոշվում է հետևյալ առնչությունից.
էջը կարելի է հաշվել կամ Պյութագորասի թեորեմով, կամ
- առնչության միջոցով։
β սուր անկյունը կարող է որոշվել հետևյալ կերպ՝
Էջն ու հակադիր սուր անկյունը[խմբագրել | խմբագրել կոդը]
Դիցուք հայտնի է էջն ու նրան հակադիր β սուր անկյունը։ ներքնաձիգը որոշվում է
առնչությունից։
էջն ու մյուս՝ α սուր անկյունը կարող են որոշվել նախորդ օրինակի նման։
Ներքնաձիգն ու սուր անկյունը[խմբագրել | խմբագրել կոդը]
Դիցուք հայտնի են ներքնաձիգն ու β սուր անկյունը։ Սուր անկյունը կարելի է հաշվել
առնչությունից։
Էջերը որոշվում են
առնչություններից։
Գնդոլորտային եռանկյունների լուծում[խմբագրել | խմբագրել կոդը]
Ընդհանուր տեսքի գնդոլորտային եռանկյունը ամբողջովին որոշվում է իր 6 բնութագիրներից (3 կողմ և 3 անկյուն) 3-ով։ Գնդոլորտային եռանկյան կողմերն ընդունված է չափել ոչ թե գծային միավորներով, այլ նրանց վրա հենված կենտրոնական անկյան մեծությամբ։
Գնդային եռանկյունաչափության մեջ եռանկյան լուծումը ունի մի շարք տարբերություններ հարթ եռանկյան լուծման հետ։ Օրինակ, 3 անկյունների գումարը կախված է եռանկյունուց, գնդային մակերևույթի գոյություն չունեն անհավասար նման եռանկյուններ, այդ պատճառով եռանկյան կառուցման խնդիրն ըստ տրված երեք անկյունների ունի միակ լուծում։ Սակայն խնդրի լուծման համար կիրառվող հիմնական առնչությունները նման են նախորդ դեպքին՝ կոսինուսների գնդոլորտային թեորեմներ և սինուսների գնդոլորտային թեորեմներ։
Մյուս առնչություններից օգտակար կարող են լինել Նեպերի համանմանության բանաձևերն[12] ու անկյան կեսի բանաձևը[13]։

Երեք կողմեր[խմբագրել | խմբագրել կոդը]
Եթե տրված են կողմերը (անկյունային միավորներով), ապա եռանկյան անկյունները որոշվում են կոսինուսների թեորեմից[14]։
- ,
- ,
- ,

Երկու կողմ և նրանցով կազմված անկյուն[խմբագրել | խմբագրել կոդը]
Դիցուք տրված են կողմերն ու նրանցով կազմված անկյունը։ կողմը որոշվում է կոսինուսների թեորեմով[14].
անկյունները կարելի է գտնել նախորդ օրինակի նման, կամ օգտվել Նեպերի համանմանության բանաձևերից.
- ,

Երկու կողմ և նրանց միջև չընկած անկյուն[խմբագրել | խմբագրել կոդը]
Դիցուք տրված են կողմերն ու անկյունը։ Լուծման գոյության համար անհրաժեշտ է հետևյալ պայմանը.
անկյունը որոշվում է սինուսների թեորեմով.
Այստեղ, հարթ եռանկյան տարբերակի նման, դեպքում հնարավոր է երկու լուծում. и .
Մնացած մեծությունները կարելի է գտնել Նեպերի համանմանության բանաձևերից[15].
- ,

Կողմն ու կից անկյունները[խմբագրել | խմբագրել կոդը]
Այս դեպքում տրված են անկյուններն ու կողմը։ անկյունը որոշվում է կոսինուսների թեորեմից[16].
- ,
Մյուս երկու անհայտ կողմերը որոշվում են Նեպերի համանմանության բանաձևերից.
կամ, օգտագործելով անկյան արժեքը կոսինուսների թեորեմում.

Երկու անկյուն և նրանց միջև չգտնվող կողմ[խմբագրել | խմբագրել կոդը]
Դիցուք տրված են անկյուններն ու կողմը։ կողմը որոշվում է սինուսների թեորեմով[17].
- ,
Եթե կողմի անկյունը սուր է և , ապա գոյություն ունի երկրորդ լուծում.
Մնացած մեծությունները որոշվում են Նեպերի համանմանության բանաձևերից.
- ,
- ,

Երեք անկյուն[խմբագրել | խմբագրել կոդը]
Եթե տրված են երեք կողմերը, անկյունները որոշվում են կոսինուսների թեորեմից.
- ,
- ,
- :
Մկ այլ տարբերակ է անկյան կեսի բանաձևը կիրառելը[18]։
Գնդոլորտային ուղիղ եռանկյունների լուծում[խմբագրել | խմբագրել կոդը]
Տրված ալգորիթմերը զգալիորեն հեշտանում են, եթե հայտնի է, որ անկյուններից մեկը (օրինակ, անկյունը) ուղիղ է։ Գնդոլորտային ուղիղ եռանկյունը ամբողջովին որոշվում է երկու տարրով, մնացած երեքը հաշվում են Նեպերի մնեմոնիկանան կանոնի կամ հետևյալ առնչությունների միջոցով.[19].
Տարբերակումներ և ընդհանրացումներ[խմբագրել | խմբագրել կոդը]
Գործնական շատ կարևոր խնդիրներում կարող են հայտնի լինել եռանկյան ուրիշ բնութագիրներ՝ օրինակ, միջնագծերը, բարձրությունները, կիսորդները, ներգծած և արտագծած շրջանագծերի շառավիղները և այլն։ Գագաթի անկյունների փոխարեն կարող են տրված լինել ուրիշ անկյուններ։ Նման խնդիրների լուծումների ալգորիթմները կազմվում են նախորդ եռանկյունաչափական թեորեմների միջոցով։
Գործնական օգտագործման օրինակներ[խմբագրել | խմբագրել կոդը]
Եռանկյունավորում[խմբագրել | խմբագրել կոդը]

Նավից ափ ընկած հեռավորությունը որոշելու համար հարկավոր է ափի վրա նշել երկու կետ, որոնց հեռավորությունը հայտնի է, չափել և անկյունները այդ կետերը միացնող գծերի և դեպի նավը տարված ուղղության միջև։ Կիրառելով «կողմն ու երկու կից անկյունները» տարբերակի բանաձևերը՝ կարելի է հաշվել եռանկյան բարձրությունը[20].
Հետևյալ մեթոդը օգտագործվում է առափնյա նավագնացությունում։ Նպանատիպ ալգորիթմ օգտագործվում է նաև աստղագիտության մեջ՝ մինչև մոտակա աստղը հեռավորությունը որոշելու համար. Երկրի ուղեծրի երկու հակադիր կետերից (այսինքն՝ կես տարվա պարբերությամբ) չափում են տվյալ աստղի դիտման անկյունները և ըստ դրանց տարբերության (պարալաքսի) հաշվում են հեռավորությունը[20]։

Ուրիշ օրինակ. հարկավոր է հաշվել լեռան կամ բարձր շինության բարձրությունը։ Հայտնի են հեռավորության վրա գտնվող եևկու կետերը ներկայացնող գագաթների անկյունները։ Նախորդ տարբերակի բանաձևերն օգտագործելով՝ կարող ենք գտնել որոնելի բարձրությունը[21].
- :
Հեռավորություն երկրագնդի երկու կետերի միջև[խմբագրել | խմբագրել կոդը]

Հարկավոր է հաշվել հեռավորությունը երկրագնդի երկու կետերի միջև[22].
- A կետ. լայնություն՝ երկայնություն՝
- B կետ. լայնություն՝ երկայնություն՝
գնդոլորտային եռանկյան համար, որտեղ -ն հյուսիսային բևեռն է, հայտնի են հետևյալ մեծությունները.
Սա «երկու կողմ և նրանց միջև ընկած անկյուն» դեպքն է։ Տրված բանաձևերից ստացվում է.
- ,
որտեղ -ը Երկրի շառավիղն է։
Պատմություն[խմբագրել | խմբագրել կոդը]
Եռանկյունաչափական գիտելիքների սերմերը կարելի է գտնել Հին Եգիպտոսի, Բաբելոնի և Հին Չինաստանի մաթեմատիկական ձեռագրերում։ Այդ շրջանի ամենակարևոր ձեռքբերումը այն առնչությունն է, որը հետագայում ստացավ Պյութագորասի թեորեմ անվանումը. Վան դեր Վարդենը կարծում է, որ բաբելոնացիները հայտնաբերել են այն մ.թ.ա. 2000-ից 1786 թվականների ընթացքում[23]։
Առաջին անգամ եռանկյունների լուծման խնդիրը (ինչպես գծային, այնպես էլ գնդային) ի հայտ է եկել հին հունական երկրաչափության մեջ[24]։ Էվկլիդեսի «Սկզբունքներ» գրքի երկրորդ հատորի 12-րդ թեորեմը բութանկյուն եռանկյունիների համար կոսինուսների թեորեմի բառային շարադրանքն է[25]։
Հաջորդ՝ 13-րդ թեորեմը կոսինուսների թեորեմն է սուրանկյուն եռանկյունների համար։ Սինուսների թեորեմի նմանօրինակը հույները չեն ունեցել, այն հայտնաբերվել է ավելի ուշ[26]. առաջին անգամ սինուսների թեորեմի ապացույցը նկարագրված է Նասրեդին Աթ-Թուսիի «Լրիվ քառանկյան մասին տրակտատ» գրքում, որը գրվել է XIII դարում[27]։
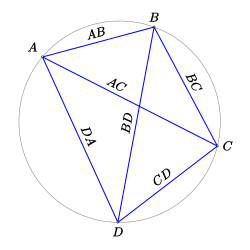
(Պտղոմեոսի թեորեմ)
Հավանաբար, առաջին եռանկյունաչափական աղյուսակները կազմել է Հիպարքոսը մ.թ.ա. II դարում աստղագիտական հաշվարկների համար։ Հետագայում աստղագետ Կլավդիոս Պտղոմեոսը իր «Ալմահեսթ»-ում լրացլել է Հիպարքոսի արդյունքները։ «Ալմահեսթ»-ի առաջին գիրքը անտիկ ժամանակաշրջանի ամենանշանակալից եռանկյունաչափական աշխատանքն է։ Մասնավորապես, «Ալմահեսթը» պարունակում է աղեղների ծավալուն աղյուսակներ ինչպես սուր, այնպես էլ բութ անկյունների համար՝ 30 րոպեին հավասար քայլերով։ Լարերը հաշվելու համար Պտղոմեոսը գրքի X գլխում օգտագործում էր Պտղոմեոսի թեորեմը (որը հայտնի էր դեռ Արքիմեդին), որը պնդում է հետևյալը.
| Շրջանագծին ներգծված ուռուցիկ բազմանկյան հանդիպակաց կողմերի երկարությունների արտադրյալների գումարը հավասար է այդ բազմանկյան անկյունագծեր արտադրյալին։ |
Այս թեորեմից դժվար չէ ստանալ երկու բանաձևեր՝ գումարային անկյան սինուսն ու կոսինուսը, ու ևս երկու բանաձևեր՝ տարբերություն անկյան սինուսն ու կոսինուսը։ Սակայն հույների մոտ բանաձևային տեսքերը բացակայում էին[1].: Պտղոմեոսը ակնհայտորեն չի ձևակերպում կոսինուսների և սինուսների բանաձևը եռանկյունների համար։ Այնուամենայնիվ նա կարողանում է լուծել խնդիրը՝ եռանկյունը բաժանելով երկու ուղղանկյուն եռանկյան[28]։
Հարթ եռանկյունաչափության հետ զուգահեռ հույները աստղագիտության ազդեցությամբ, լայնորեն զարգացրեցին սֆերիկ եռանկյունաչափությունը։ Էվկլիդեսի «Սկզբունքներում» սֆերիկ եռանկյունաչափությանն առնչվող միայն մի քանի թեորեմ կա, որոնք նվիրված են տարբեր տրամագծերով գնդերի ծավալների հարաբերություններին։ աստղագիտության ու քարտեզագրության մեջ խիստ պահանջված լինելու շնորհիվ այս բնագավառն սկսեց արագորեն զարգանալ։ Սֆերիկ եռանկյունաչափությունը կիրառվում է նաև երկնային կոորդինատների, քարտեզագրական պրոյեկցիաների մեջ (մասնավորապես՝ աստրոլաբիա[29])։
Տեսության զարգացման վճռական փուլը Մենելայոս Ալեքսանդրիացու «Սֆերիկա» մենագրությունն էր(մոտավորապես մեր թվարկության 100 թվական)։ Առաջին գրքում նա նկարագրում է սֆերիկ եռանկյուների մասին թեորեմները, Էվկլիդեսի անալոգային թեորեմները՝ հարթ եռանկյուների մասին։ Պատմաբանները կարծում են, որ Մենելայոսի մոտեցումը շատ առումներով հիմնվում է Թեոդոսիոսի աշխատության վրա, սակայն Մենելայոսը առավել խորացված է ներկայացրել եզրակացություններն ու ավելացրել նորերը։ Համաձայն Պապուս Ալեքսանդրիացու հաղորդագրության՝ Մենելայոսն առաջինն էր, ով սֆերիկ եռանկյունը դիտարկեց որպես առանձին մարմին, այն ներկայացնելով գնդի հատվածների միջոցով[30]։ Մենելայոսն ապացուցել է մի թեորեմ, որի վերաբերյալ Եվկլիդեսը չունի հարթ անալոգ. երկու սֆերիկ եռանկյուններ համատեղելի են, եթե համապատասխան անկյունները հավասար են։ Մեկ այլ թեորեմում նա պնդում է, որ սֆերիկ եռանկյան անկյունների գումարը միշտ մեծ է 180°[30]:
Մի քանի տասնամյակ անց Կլավդիոս Պտղոմեոսն իր «Երկրաչափություն», «Անալեմա» և «Պլանիսֆերաներ» աշխատություններում տալիս է եռանկյունաչափական արտահայտությունների հստակ կիրառությունը քարտեզագրության, աստղագիտության ու մեխանիկայի մեջ։ Այդ ամենի հետ մեկտեղ, գրքում նկարագրված է ստերեոգրաֆիկ պրոյեկցիան ու բացատրված՝ մի քանի կոնկրետ առաջադրանք. գտնել երկնային լուսատուի բարձրությունն ու ազիմուտը՝ կախված նրա թեքումից ու ժամային անկյունից։ Եռանկյունաչափության տեսանկյունից դա նշանակում է, որ պետք է գտնել սֆերիկ եռանկյան կողմն ըստ մյուս երկու կողմերի ու հանդիպակաց անկյան[31]։

4-րդ դարում անտիկ գիտության անկումից հետո մաթեմատիկայի զարգացման կենտրոնը տեղափոխվեց Հնդկաստան։ Հնդիկ մաթեմատիկոսների աշխատությունները՝ սիդհանթերը, ցույց են տալիս, որ նրանք քաջատեղյակ են եղել հույն երկրաբանների ու աստղագետների աշխատություններին[32]։ Հնդիկները քիչ էին հետաքրքրվում զուտ երկրաչափությամբ, բայց նրանց ներդրումը կիրառական աստղագիտության ու եռանկյունաչափության հաշվարկման բնագավառների մեջ անփոխարինելի է։ Հնդիկներն առաջինն էին, որ օգտագործեցին կոսինուսը։ Կիրառվում էր նաև, այսպես կոչված, հակադարձ սինուսը, կամ սինուս-վերզուսը, որը աջ մասի նկարում հավասար է DC հատվածի երկարությանը[33]։
Աստղագիտական խնդրների լուծման բնագավառում հնդիկները ահռելի հաջողությունների են հասել[32]։ Օրինակ՝ Վարահամիհիրի (7-րդ դար) «Պանչա-սիդհանթիկայում» տրվում է Պտղոմեոսի կողմից նկարագրված աստղագիտական խնդրի յուրօրինակ լուծում. գտնել Արևի բարձրությունը հորիզոնից, եթե հայտնի է տեղանքի լայնությունը, Արեգակի թեքումն ու ժամային անկյունը։ Լուծման համար հեղինակը կիրառում է կոսինուսների թեորեմի անալոգը[34]։ Հենց նա է առաջին անգամ ստացել կես անկյան սինուսի բանաձևը[35]։
8-րդ դարում Մերձավոր ու Միջին Արևելքի երկրներ հասան հին հունական ու հնդկական մաթեմատիկոսների ու աստղաբանների աշխատություններին։ Այդ աշխատությունները արաբերեն թարգմանելու գործով զբաղվել են 8-րդ դարի լեգենդար գիտնականներ Իբրահիմ Ալ-Ֆազարին և Յակուբ իբն Տարիկը։
Նրանց աստղագիտական տրակտատները, հնդկական սիդհաների օրինակով, կոչվում էին «զիջեր». տիպիկ զիջն իրենից ներկայացնում էր աստղագիտական ու եռանկյունաչափական աղյուսակների հավաքածու, որտեղ աղյուսակները դասավորված էին օգտագործելիության[36]։ 8-13-րդ դարերի զիջերի ուսումնասիրությունները ցույց են տալիս, որ այդ ժամանակ եռանկյունաչափության վերաբերյալ գիտելիքներն արագորեն համալրվում էին։ Իսլամական գիտնականների համար առավել հետաքրքիր էր սֆերիկ եռանկյունաչափությունը, որի միջոցով հնարավոր էր իրականացնել աստղագիտական ու գեոդեզիական հաշվարկներ[37]։
Սաբիտ իբն Կուրան (9-րդ դար) և Ալ-Բատանին (10-րդ դար) առաջինը բացահայտեցին սինուսների հիմնական թեորեմը մասնավոր ուղղանկյուն սֆերիկ եռանկյան համար։ Սֆերիկ եռանկյան թեորեմի ապացույցը տվեցին (տարբեր եղանակներով, և, հավանաբար, միմյանցից անկախ) Աբու լ Վաֆան, ալ-Հուջանին ու իբն Իրաքին 10-րդ դարի վերջում[26]։ Իր մեկ այլ տրակտատում իբն Իրաքը ձևակերպել ու ապացուցել է սինուսների թեորեմը հարթ եռանկյան համար[38]։
Կոսինուսներ իսֆերիկ թեորեմը իսլամական երկրներում ընդհանուր տեսքով ձևակերված ու ապացուցված չէր, բայց Սաբիտ իբն Կուրայի, ալ-Բատանիի ու մյուս աստղաբանների աշխատանքներում կան դրան համարժեք պնդումներ։ Ռեգիոմոնտանը, ով առաջինը տվեց այդ կարևորագույն կախվածության ձևակերպումը (15-րդ դար), դրան տվեց «Ալբատենիայի թեորեմ» (այն ժամանակ Եվրոպայում այդպես էին անվանում ալ-Բատանիին)[39]։
Եռանկյունաչափության, որպես առանձին գիտության հիմնարար հասկացությունները (ինչպես հարթաչափական, այնպես էլ սֆերիկ) տվել է պարսիկ մաթեմատիկոս ու աստղաբան Նասրեդին Թուսին 1260 թվականին[40]։ Նրա «Աշխատություն ուռուցիկ քառանկյան մասին» աշխատությունը պարունակում է տիպիկ խնդիրների, այդ թվում՝ բարդ վարժությունների պրակտիկ լուծումներ, որոնք լուծել է հենց աթ-Թուսին, օրինակ՝ սֆերիկ եռանկյան կառուցումն ըստ տրված երեք անկյունների[41]։ Ձևակերպված է տանգենսների թեորեմը սֆերիկ եռանկյունների համար, նկարագրված է կարևոր բևեռային եռանկյուններ հասկացությունը (առաջին անգամ օգտագործել են 11-րդ դարում Իբն Իրաքին ու ալ-Ջայանին)։ Աթ-Թուսիի աշխատությունները լայնորեն հայտնի են եղել Եվրոպայում ու խստորեն ազդել են եռանկյունաչափության հետագա զարգացման վրա։
Նոր ժամանակներում եռանկյունաչափության զարգացումը չափազանց կարևոր էր ոչ միայն աստղաբանության ու աստղագիտության զարգացման համար, այլ նաև այլ ոլորտների համար, այդ թվում հրետանու, օպտիկայի, ծովային հեռավոր ճանապարհորդությունների կազմակերպման համար։ Այդ իսկ պատճառով 16-րդ դարում այդ թեմայով սկսեցին զբաղվել այնպիսի մեծանուն գիտնականներ, ինչպիսիք են Նիկոլայ Կոպեռնիկոսը, Յոհան Կեպլերը, Ֆրանսուա Վիետը։ Կոպեռնիկոսը եռանկյունաչափությանն է նվիրել իր «Երկնայի գնդերի պտույտի մասին» (1543) տրակտատի երկու գլուխներ։ Շուտով (1551) հայտնվեցին Կոպեռնիկոսի աշակերտի՝ Ռետիկի տասնհինգանիշ եռանկյունաչափական աղյուսակները՝ 10" քայլով[42]։ 1604 թվականին Կեպլերը հրապարակում է «Աստղագիտության օպտիկական մաս» աշխատությունը։ Բարդ եռանկյունաչափական հաշվարկների անհրաժեշտություն առաջացավ 17-րդ դարի սկզբում, լոգարիթմների հայտնաբերմամբ։ Ընդ որում, Ջոն Նեպերի առաջին լոգարիթմական աղյուսակները պարունակում էին միայն եռանկյունաչափական ֆունկցիաների լոգարիթմներ։ Նեպերի այլ հայնտագործությունների ցանկում կարևոր էին սֆերական եռանկյունների լուծման նպատակահարմար մեթոդները, որոնք ստացել են «Նեպերի անալոգիայի բանաձևեր» անվանումը[43]։ Եռանկյունաչափության բնագավառում աշխատանքներ տարել են 17-րդ դարի այնպիսի նշանավոր մաթեմատիկոսներ ինչպիսիք են Օտրեդը, Հյուգենսը, Օզանամը, Վալլիսը։ 17-րդ դարի երկրորդ կեսում նշանավոր պրոցես էր եռանկյունաչափության հանրահաշվացումը, դրա սիմվոլիկայի կատարելագործումն ու պարզեցումը (չնայած Էյլերից առաջ սիմվոլիկան ավելի բարդ էր քան այժմ)[44]։
Տես նաև[խմբագրել | խմբագրել կոդը]
Գրականություն[խմբագրել | խմբագրել կոդը]
- Տեսություն և ալգորիթմներ
- Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия: 7-9 классы. Учебник для общеобразовательных учреждений. — 19-е изд.. — М.: Просвещение, 2009. — 384 с. — ISBN 978-5-09-021136-9
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия, учебник для 10 класса. — М.: МЦНМО, 2002. — ISBN 5-94057-050-X
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Мензел Д. (ред.) Основные формулы физики. Глава 1. Основные математические формулы. — М.: Изд. иностранной литературы, 1957. — 658 с.
- Основные понятия сферической геометрии и тригонометрии // Տարրական մաթեմատիկայի հանրագիտարան (5 գիրք). — М.: Физматгиз, 1963. — Т. 4. — С. 518-557. — 568 с.
- Степанов Н. Н. Сферическая тригонометрия. — М.-Л.: ОГИЗ, 1948.
- Պատմություն
- Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76-95. — 240 с.
- Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- Մաթեմատիկայի պատմություն. Հին ժամանակների սկզբից մինչև նոր ժամանակներ // Մաթեմատիկայի պատմություն / Под редакцией Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // Մաթեմատիկայի պատմություն / Под редакцией Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // Մաթեմատիկայի պատմություն / Под редакцией Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9
- Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
- Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
- Цейтен Г. Г. История математики в древности и в средние века. — М.-Л.: ГТТИ, 1932. — 230 с.
- Цейтен Г. Г. История математики в XVI и XVII веках. — М.-Л.: ОНТИ, 1938. — 456 с.
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ 1,0 1,1 Выгодский М. Я., 1978, էջ 266-268.
- ↑ Элементарная математика, 1976, էջ 487.
- ↑ «Solving Triangles». Maths is Fun. Վերցված է 23 Jule 2012-ին.
- ↑ Элементарная математика, 1976, էջ 488.
- ↑ Степанов Н. Н., 1948, էջ 133.
- ↑ «Solving SSS Triangles». Maths is Fun. Արխիվացված օրիգինալից 2012 թ․ սեպտեմբերի 30-ին. Վերցված է 23 Jule 2012-ին.
- ↑ «Solving SAS Triangles». Maths is Fun. Արխիվացված օրիգինալից 2012 թ․ սեպտեմբերի 30-ին. Վերցված է 24 Jule 2012-ին.
- ↑ «Solving SSA Triangles». Maths is Fun. Արխիվացված օրիգինալից 2012 թ․ սեպտեմբերի 30-ին. Վերցված է 24 Jule 2012)-ին.
- ↑ Выгодский М. Я., 1978, էջ 294.
- ↑ Элементарная математика, 1976, էջ 493-496.
- ↑ «Solving ASA Triangles». Maths is Fun. Արխիվացված օրիգինալից 2012 թ․ սեպտեմբերի 30-ին. Վերցված է 24 Jule 2012-ին.
- ↑ Степанов Н. Н., 1948, էջ 87-90.
- ↑ Степанов Н. Н., 1948, էջ 102-104.
- ↑ 14,0 14,1 Энциклопедия элементарной математики, 1963, էջ 545.
- ↑ Степанов Н. Н., 1948, էջ 121-128.
- ↑ Степанов Н. Н., 1948, էջ 115-121.
- ↑ Степанов Н. Н., 1948, էջ 128-133.
- ↑ Степанов Н. Н., 1948, էջ 104-108.
- ↑ Основные формулы физики, 1957, էջ 14-15.
- ↑ 20,0 20,1 Геометрия: 7-9 классы, 2009, էջ 260-261.
- ↑ Геометрия: 7-9 классы, 2009, էջ 260
- ↑ Степанов Н. Н., 1948, էջ 136-137.
- ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5
- ↑ Глейзер Г. И., 1982, էջ 77.
- ↑ Глейзер Г. И., 1982, էջ 94-95.
- ↑ 26,0 26,1 Матвиевская Г. П., 2012, էջ 92-96.
- ↑ Berggren, J. Lennart (2007). «Mathematics in Medieval Islam». The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. էջ 518. ISBN 9780691114859.
- ↑ Ван дер Варден Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — С. 366. — 456 с.
- ↑ Матвиевская Г. П., 2012, էջ 25-27.
- ↑ 30,0 30,1 Матвиевская Г. П., 2012, էջ 33-36.
- ↑ Цейтен Г. Г., 1932, էջ 158-162.
- ↑ 32,0 32,1 Матвиевская Г. П., 2012, էջ 40-44.
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, էջ 79.
- ↑ История математики, том I, 1970, с. 199-201.
- ↑ История математики в Средние века, 1961, էջ 157.
- ↑ Матвиевская Г. П., 2012, էջ 51-55.
- ↑ Хрестоматия по истории математики, 1976, էջ 204-205
- ↑ Матвиевская Г. П., 2012, էջ 111.
- ↑ Матвиевская Г. П., 2012, էջ 96-98.
- ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
- ↑ Рыбников К. А., 1960, էջ 105.
- ↑ История математики, том I, 1970, էջ 320.
- ↑ Степанов Н. Н. §42. Формулы «аналогии Непера» // Сферическая тригонометрия. — М.-Л.: ОГИЗ, 1948. — С. 87-90. — 154 с.
- ↑ Вилейтнер Г., 1960, էջ 327-335.
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի օրվա հոդված: |














































































































