Եռանկյան անհավասարություն

x, y, z կողմերով եռանկյան մեջ (x + y)-ը միշտ մեծ է z -ից

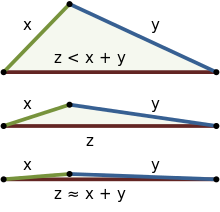
Եռանկյան անհավասարություն, երկրաչափության , ֆունկցիոնալ վերլուծության և դրանց առնչվող առարկաներում հեռավորության ինտուիտիվ հատկություններից մեկը։ Այն պնդում է, որ եռանկյան ցանկացած կողմի երկարությունը միշտ փոքր է, քան մյուս 2 կողմերի երկարությունների գումարը։ Եռանկյան անհավասարությունը չափային տարածության, նորմայի և այլնի սահմանման մեջ, ներառված է որպես աքսիոմ։ Դա հաճախ նաև թեորեմ է հանդիսանում տարբեր տեսություններում։

Էվկլիդեսյան երկրաչափություն

Էվկլիդեսյան երկրաչափության եռանկյան անհավասարության պացույց

Դիցուք՝ տրված է $\Delta ABC.$ և $|AC|\leqslant |AB|+|BC|,$ ընդորում $|AC|=|AB|+|BC|$ ստացվում է միայն այն դեպքում, երբ եռանկյան մեջ $B$ գտնվում է $A$ և $C$ կետերի միջև, մի ուղղի վրա։

BD- ն՝ AB- ի շարունակությունն է (ըստ կառուցման):Ընդորում, β> α և AD> AC: Սակայն AD = AB + BD = AB + BC, այնպես, որ AB + BC> AC: Այս ապացույցը բերվում է Էվկլիդեսի տեսությունում( Գիրք 1)։

Ապացուցում է եռանկյան անհավասարությունը հետևյալ կերպ։ Նախ՝ ապացուցվում է թեորեմ այն մասին, որ եռանկյան արտաքին անկյունը մեծ է ներքին անկյունից, որը նրան կից չէ։ Դրանից բխում է թեորեմ,որ եռանկյունու մեծ կողմի հանդիպակած անկյունը մեծ է։ Հետագայում, օգտագործելով հակառակ եղանակը, մենք ապացուցում ենք այն թեորեմը, որ եռանկյան ավելի մեծ ներքին անկյան դիմաց գտնվում է մեծ կողմը, և այս թեորեմից դուրս է բերում եռանկյան անհավասարությունը։

Նորմավորված տարածություն

Դիցուք՝ $(X,\|\cdot \|)$֊ն նորմավորված վեկտորական տարածությունն է, որտեղ $X$֊ը կամայական բազմություն է իսկ $\|\cdot \|$֊ը $X$֊ի վրա որոշված նորմ։ Այդ դեպքում ըստ վերջինիս սահմանման ճիշտ է հետևյալ անհավասարությունը․

$\|x+y\|\leqslant \|x\|+\|y\|,\quad \forall x,y\in X.$

Մետրիկական տարածություն

Դիցուք՝ $(X,\rho )$֊ն մետրիկական տարածություն է, որտեղ $X$-ը կամայական բազմություն է, իսկ $\rho$-ն $X$ -ի վրա որոշված մետրիկա։ Ըստ վերջինիս սահմանման

$\rho (x,y)\leqslant \rho (x,z)+\rho (z,y),\quad x,y,z\in X.$

Տարբերակում և ընդհանրացում

• $d(x,z)\leqslant \max(d(x,y),d(y,z))$ Եռանկյան մեծ անհավասարություն

Եռանկյան հակառակ անհավասարություն

Մետրական և նորմավորված տարածությունում եռանկյան անհավասարության հետևանքն է հանդիսանում հետևյալ անհավասարությունը․

• $|\rho (x,y)-\rho (x,z)|\leqslant \rho (y,z),\quad x,y,z\in X.$

Եռանկյան անհավասարությունը եռանիստ անկյան համար

Ուռուցիկ եռանիստ անկյան յուրաքանչյուր հարթ անկյուն փոքր է մյուս երկու հարթ անկյունների գումարից։

Կետերի կամայական թիվ

Նշանակենք $\rho (x_{i},x_{j})$֊ով $x_{i}$ և $x_{j}$ կետերի հեռավորությունը։ Այդ դեպքում տեղի ունի հետևյալ անհավասարությունը՝ $\rho (x_{1},x_{m})\leqslant \rho (x_{1},x_{2})+\rho (x_{2},x_{3})+...+\rho (x_{m-1},x_{m})$։ Անհավասարությունը ստացվում է երեք կետերի համար եռանկյան անհավասարությունը հաջորդաբար կիրառելով․

$\rho (x_{1},x_{m})\leqslant \rho (x_{1},x_{2})+\rho (x_{2},x_{m})\leqslant \rho (x_{1},x_{2})+\rho (x_{2},x_{3})+\rho (x_{3},x_{m})\leqslant ...$

Ծանոթագրություններ

Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Եռանկյան անհավասարություն» հոդվածին։