Օհմի օրենք
| Այս հոդվածն աղբյուրների կարիք ունի։ Դուք կարող եք բարելավել հոդվածը՝ գտնելով բերված տեղեկությունների հաստատումը վստահելի աղբյուրներում և ավելացնելով դրանց հղումները հոդվածին։ Անհիմն հղումները ենթակա են հեռացման։ |
| Էլեկտրամագնիսականություն |
|---|
| Մագնիսականություն |
Օհմի օրենք, էլեկտրական շղթայի հիմնական օրենքներից մեկը։ Հոսանքի մեծությունը ուղիղ համեմատական է հաղորդչի լարմանը և հակադարձ համեմատական է նրա դիմադրությանը:
Հաստատուն հոսանքի շղթայում հաղորդչի ծայրերում եղած պոտենցիալների տարբերության և հաղորդչով անցնող հոսանքի մեծության միջև գոյություն ունի ուղիղ համեմատական կախում:
- որտեղ I-ն հաղորդչով անցնող հոսանքն է (Ամպեր), U_ն լարումը (Վոլտ), իսկ R_ը հաղորդչի դիմադրությունն է(համեմատականության գործակից)(Օհմ), և կախված է հաղորդչի չափերից , ջերմաստիճանից և նյութի տեսակից:
Համեմատականության R գործակիցը կոչվում է օհմական դիմադրություն կամ պարզապես հաղորդիչի տվյալ տեղամասի դիմադրություն։ Հայտնագործել է Գեորգ Օհմը 1826 թ-ին։
Ընդհանուր դեպքում I-ի և U-ի կախումը ոչ գծային է, սակայն գործնականում, լարումների որոշակի միջակայքում այն կարելի է համարել գծային և կիրառել Օհմի օրենքը։ Վերը գրված տեսքով Օհմի օրենքը ճիշտ է շղթայի՝ էլշուի աղբյուրներ չպարունակող տեղամասերի համար։ Այդպիսի աղբյուրների (կուտակիչ գեներատորներ են) առկայության դեպքում Օհմի օրենքն ունի
տեսքը, որտեղ -ն տվյալ տեղամասում պարունակվող բոլոր աղբյուրների էլշուն է։
Օհմի օրենքի ընդհանրացումը ճյուղավորված շղթայի համար Կիրխհոֆի երկրորդ կանոնն է։
Օհմի օրենքը փակ շղթայի համար[խմբագրել | խմբագրել կոդը]
Փակ շղթայի համար Օհմի օրենքը ստանում է տեսքը, որտեղ -ը շղթայի լրիվ դիմադրությունն է՝ արտաքին R և էլշուի աղբյուրի ներքին Ri դիմադրությունների գումարը։
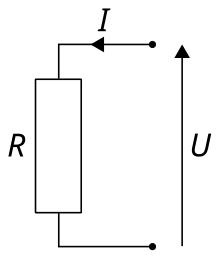
I-հոսանքի ուժ
R-շղթայի դիմադրություն
Հաղորդման հոսանք կոչում են էլեկտրական լիցքեր կրող մասնիկների շարժումը (կարգավորված կամ քաոսային) նյութական մարմինների ներսում էլոկտրական դաշտի ազդեցության տակ։
հ
Օհմի օրենքը դիֆերենցիալ տեսքով[խմբագրել | խմբագրել կոդը]
Հաղորդման հոսանք են կոչում էլեկտրական լիցքեր կրող մասնիկների շարժումը (կարգավորված կամ քաոսային) նյութական մարմինների ներսում էլեկտրական դաշտի ազդեցության տակ։

Նկարից երևում է, որ տվյալ համակարգը լրիվ կբնութագրվի ոչ միայն Ι հոսանքի արժեքով, որ հոսում է արտաքին շղթայով, այլ նաև լիցքավորված մասնիկների շարժման ուղղության և ինտենսիվության տվյալներով տարածքի ամեն կետում։
Այդ նպատակով ներմուծենք նոր հասկացություն` հաղորդման հոսանքի խտությունը.
որտեղ N-ը 1 մ նյութում լիցքը կրող մասնիկների թիվն է
e - ն`լիցքը,
V - ն` կրողների արագությունը տվյալ կետում
Ա/մ
- կրող մասնիկների արագության վեկտորին ուղղահայաց միավոր հարթության միջով անցնող հոսանքի չափն է։
Մասնիկների արագությունը, հետևաբար և հաղորդման հոսանքի խտությունը, ուղիղ համեմատական է էլեկտրական դաշտի լարվածությանը.
(1)
ուր -ն ինչ-որ մի չափ ունեցող հաստատուն է։
Ապացուցենք, որ (1)-ը Օհմի գրառման տեսքերից մեկն է։

Այդ նպատակով դիտարկենք կողով մի խորանարդ։ Ենթադրենք նաև, որ երկու հակադիր նիստերը մետաղացված են, և նրանց վրա U պոտենցիալի մեծության տարբերություն կա։ Այսինքն, շղթայով կհոսի I հոսանք։
,
Օգտագործելով (1)` կստանանք`
Ընդունենք` ,
որտեղ R-ը նիստերի միջև եղած դիմադրությունն է։
(1) բանաձևը կոչվում է Օհմի օրենք դիֆերենցիալ տեսքով, քանի որ ներկայացնում է հաղորդման հոսանքի խտության և էլեկտրական դաշտի լարվածության կապը տարածության ցանկացած կետի անվերջ փոքր մոտակայքում։
Պարզ է, որ գործակիցը Սիմ/մ չափ ունի։ Այն կոչվում է տեսակարար ծավալային հաղորդականություն և բնութագրում է նյութի հաղորդիչ հատկությունները։
| Մետաղ | Սիմ/մ |
|---|---|
| Արծաթ | 6,1 |
| Պղինձ | 5,7 |
| Ալյումին | 3,2 |
Այսպիսով, մետաղի մակերեսին բավականին մեծ հոսանքի ստեղծման համար բավական է էլեկտրական դաշտի լարվածության չնչին մեծության առկայությունը։ Դիէլեկտրիկների և կիսահաղորդիչների տեսակարար ծավալային հաղորդականությունը շատ ավելի փոքր է, քան մետաղներում։ Այդ պատճառով հարմար է այդ նյութերի էլեկտրահաղորդականությունը արտահայտել այլ մեծությամբ - դիէլեկտրիկ կորուստների անկյան միջոցով։
Օհմի օրենքը կարելի է գրել դիֆերենցիալ տեսքով՝
կամ
- ,
որտեղ -ն հոսանքի խտությունն է, ρ-ն՝ հաղորդչի տեսակարար դիմադրությունը, σ=1/ρ-ն՝ տեսակարար էլեկտրահաղորդականությունը, -ն՝ պոտենցիալ էլեկտրական դաշտի լարվածությունը, -ն՝ ոչ էլեկտրաստատիկ բնույթի ուժերի (ինդուկցիոն, քիմիական, ջերմային ևն) ստեղծված կողմնակի դաշտի լարվածությունը։
Օհմի օրենքը կոմպլեքս տեսքով ճիշտ է նաև սինուսարդային քվազիստացիոնար հոսանքների համար.
- ,
որտեղ -ը լրիվ կոմպլեքս դիմադրությունն է (R-ը շղթայի ակտիվ դիմադրությունն է, x-ը ռեակտիվ դիմադրությունը)։
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Օհմի օրենք» հոդվածին։ |
| ||||||










![{\displaystyle [j_{h}]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5258fd800ce3003ab9d5842fde592a168ecb4a0e)
















