Ալիքատար
| Էլեկտրամագնիսականություն |
|---|
| Մագնիսականություն |
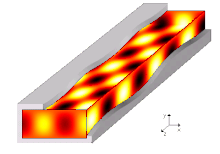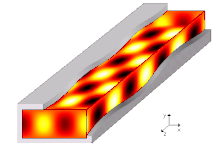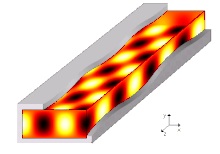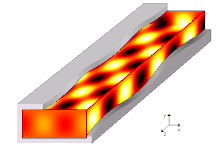
Ալիքատար, ռադիոալիքատար, սնամեջ կամ դիէլեկտրիկով լցված հաղորդիչ խողովակ (սովորաբար ուղղանկյուն կամ կլոր կտրվածքով), ծառայում է գերբարձր հաճախականության էլեկտրամագնիսական ալիքների ուղղորդված հաղորդում։ Ալիքատարը խողովակ է, որի միջով տարածվող ալիքները ինչ-որ չափով թուլանում են։ Այդ դեպքում ալիքային դաշտը կենտրոնանում է խողովակի ներսում կամ նրան հարող տարածքում։ Գերբարձր հաճախականության տեխնիկայում հաղորդման ալիքատար գծերը լայն կիրառություն ունեն։ Հաղորդման ալիքատար գծերի օգտագործման դեպքում անհրաժեշտ է իմանալ ալիքատարներում ալիքների գրգռման և տարածման միջոցները, ինչպես նաև դրանց համաձայնեցման մեթոդները։ Այս տվյալները ուղղակիորեն կախված են ալիքատարում դաշտի կառուցվածքից։
Ալիքների տիպերը ալիքատարում[խմբագրել | խմբագրել կոդը]
Ցանկացած ձև ունեցող ալիքատարում կարող են երկու տիպի ալիքներ լինել.
- Լայնակի էլեկտրական ալիք- TE տիպի ալիքն է, որն իր տարածման, այսինքն՝ ալիքատարի առանցքի ուղղությամբ չունի էլեկտրական դաշտի բաղադրիչ։ Այդ տիպի ալիքի էլեկտրական դաշտի լարվածության վեկտորը գտնվում է ալիքատարի առանցքին ուղղահայաց մակերևույթում, իսկ մագնիսական դաշտի լարվածության վեկտորն ունի երկայնակի բաղադրիչ։ Այդ պատճառով ալիքների այդ տիպը հաճախ անվանում են H տիպի։
- Լայնակի մագնիսական ալիք- TM տիպի ալիքն է, որը մագնիսական դաշտի բաղադրիչ չունի իր տարածման ուղղությամբ։ Այդ տիպի ալիքի մագնիսական դաշտի լարվածության վեկտորը գտնվում է ալիքատարի առանցքին ուղղահայաց գտնվող մակերևույթում, իսկ էլեկտրական դաշտի լարվածության վեկտորն ունի լայնակի բաղադրիչ։ Այդ պատճառով ալիքի այդ տիպը հաճախ կոչում են E տիպի ալիք։
Ալիքատարներում, ինչպես որոշակի պարամետրեր ունեցող համակարգերում, հնարավոր է դիսկրետ(ոչ շատ ուժեղ կլանման դեպքում) տատանումների համակարգի գոյությունը։ Յուրաքանչյուր տեսակի ալիք տարածվում է ըստ իր փուլային և խմբային արագությունների։ Բոլոր տեսակի ալիքները ունեն կորուստներ, քանի որ նրանց փուլային արագությունը կախված է հաճախությունից։ Պաշտպանված ալիքատարներում փուլային արագությունը սովորաբար գերազանցում է ազատ տարածությունում տարածվող նույնատիպ ալիքի արագությանը (լույսի, ձայնի արագություն)։ Այդպիսի ալիքները կոչվում են արագ։ Իսկ չպաշտպանված ալիքատարներում նրանք կարող են անցնել ալիքատարի պատերի միջով և դուրս գալ շրջակա միջավայր։ Այդպիսի ալիքները կոչվում են վազող։

Էլեկտրամագնիսական ալիքը կարելի է ուղղորդել տարածության մեջ անվերջ հաղորդիչ հարթության միջոցով։ Էլեկտրամագնիսական էներգիան տարածության մեջ ավելի լավ կարելի է սահմանափակել, եթե հաղորդիչ հարթությանը զուգահեռ, նրանից մի որոշակի տարածության վրա տեղադրվի երկրորդ հարթություն այնպես, որ ալիքները տարածվեն միայն այդ հարթությունների արանքում։ Այդպիսի ուղղորդող համակարգը կոչվում է երկհարթային ալիքատար։
Հիմնական TEM տիպի ալիք[խմբագրել | խմբագրել կոդը]
Ե՛վ էլեկտրական, և՛ մագնիսական վեկտորների երկայնակի բաղադրիչներ չունեցող ալիքները կոչվում են լայնակի էլեկտրամագնիսական՝ TEM ալիքներ։ Երկհարթային ալիքատարում TEM ալիքների հիմնական հատկություններից են.
- 1. Քանի որ E-ի սահմանային պայմանները ինքնաբերաբար բավարարված են, դաշտի կառուցվածքը կախված չէ λ-ից և հարթությունների միջև եղած տարածություններից։ Հետևաբար`
այսինքն՝ համակարգը բաց է թողնում բոլոր հաճախականությունների տատանումները՝ ընդհուպ մինչև հաստատուն հոսանք։
- 2. TEM - տիպի ալիքի տարածման սկզբունքը կապված չէ պատերից բազմաթիվ անդրադարձումների հետ։ Այդ պատճառով
- ,
որտեղ λ -ն համասեռ հարթ ալիքի երկարությունն է հարթությունների միջև առկա դիէլեկտրիկում։
TEM տիպի ալիքի բնութագրային դիմադրությունը (WTEM), որը հավասար է էլեկտրական և մագնիսական դաշտերի ամպլիտուդների հարաբերությանը, համընկնում է անսահման տարածությունում համասեռ հարթ էլեկտրամագնիսական ալիքի բնութագրային դիմադրության հետ։
Մաթեմատիկորեն կարելի է ճշգրիտ ապացուցել, որ TEM ալիքների տարածումը հնարավոր է միայն այն հաղորդման գծերում, ուր կան առնվազն երկու իրարից մեկուսացված հոսանքատար հաղորդիչներ, որոնց միջև պոտենցիալների տարբերություն է ստեղծված։ ԳԲՀ տեխնիկայում TEM ալիքների հաղորդման գծերից առավել հաճախ օգտագործվողը համառանցք հաղորդման գիծն է։
H10 հիմնական տիպի ալիքներ[խմբագրել | խմբագրել կոդը]



H10 ալիքը հիմնական մագնիսական ալիք է։
ԳԲՀ (գերբարձր հաճախություն) տեխնիկայում ուղանկյուն ալիքատարում որպես պարզագույն ալիքի տիպ համարվում է H10 ( կամ H01 ) ալիքը։
H10 տիպի ալիքի առավելությունը դա նրա պարզագույն կառուցվածքն է և բնութագրվում է նվազագույն մարումնորով։
Ալիքի տիպի ինդեքսները որոնք, համապատասխանաբար m և n, H10 ալիքի համար m=1 n=0 հնարավոր արժեքներն են։ Ինդեքսները նշանակում են, որ ալիքատարի լայնքով (x առանցքի գծով) տեղավորվում է դաշտի մեկ կանգուն կիսաալիք, իսկ (y առանցքի գծով) դաշտի կազմարարների ամպլիտուդները մնում են անփոփոխ։
H10 կրտիկական երկարությունը , որը ալիքի առավելագույն կրտիկական երկարությունն է, որը հավասար է 2a։
ալիքատարային ալիքի պատկերացմանը, որպես ալիքատարի պատերից անդրադարձող հարթ ալիքների անվերջ հաջորդականություն (նկ.3)։
Ալիքատարում էլեկտրամագնիսական դաշտի էներգիան կարելի է բաժանել երկու տեսակի.
1) ակտիվ էներգիան, որը տեղափոխվում է z առանցքի ուղղությամբ,
2) ռեակտիվ (կուտակված էներգիան), որը կապված է x առանցքի երկայնքով լայնակի կանգուն ալիքների գոյացման հետ։
H10 տիպի ալիքի ուղղանկյուն ալիքատարով տեղափոխված հզորությունը[խմբագրել | խմբագրել կոդը]
Տատանումների ցանկացած տիպի համար z առանցքով տեղափոխված հզորությունը կորոշվի՝ որպես Պոյնտինգի վեկտորի երկայնակի բաղադրիչի միջին արժեքի ինտեգրալ, որ վերցված է ալիքատարի լայնակի հատույթով։
Գտնենք H (վեկտոր) տիպի ալիքի Պ (վեկտոր) երկայնակի բաղադրիչը։ Էլեկտրական դաշտի միակ բաղադրիչը՝ Ė- ը կլինի՝
որտեղ Emax -ը էլեկտրական դաշտի լարվածության ամպլիտուդի մեծագույն արժեքն է, որը առկա է ալիքատարի կենտրոնական հատույթում, երբ x=α/2 ։ Օգտագործելով ալիքատարի բնութագրային դիմադրություն հասկացությունը՝ գտնում ենք մագնիսական դաշտի լայնակի բաղադրիչը։
Ընտրում ենք բացասական նշանը, որ էներգիայի հոսքը ուղղվի z առանցքի դրական ուղղությամբ։
Գտնելով Ē դաշտի ամպլիտուդի և H դաշտի համալուծ ամպլիտուդի վեկտորային արտադրյալը, կստանանք Պ միջին արժեքը։
Ինտեգրենք, հաշվի առնելով, որ
Կստանանք
Ուղղանկյուն ալիքատարները կիրառվում են 50 սմ -ից 1 մմ ալիքի երկարության տիրույթներում։ Ավելի մանրամասնեցնելով, որպես հաղորդման գծեր դեցիմետրային տիրույթում ալիքատարներն օգտագործվում են միայն բարձր հզորության սարքերում, իսկ սկսած մոտ 6 սմ ալիքի երկարությունից՝ կիրառվում են ամենուր։ Սնամեջ մետաղյա ալիքատարների լայն կիրառելիությունը պայմանավորված է դրանց մի շարք առավելություններով. ալիքատարային կոնստրուկցիաները տեխնոլոգիապես շատ են հարմար, մարումը ցածր է, մեծագույն իմպուլսային հզորություններ հաղորդելու հնարավորություն կա։
Նշենք, որ հաճախականության ցանկացած տիրույթի համար գոյություն ունեն ստանդարտ ալիքատարներ, որոնց չափսերը բերվում են տեղեկատուներում։ Օրինակ,

Ալիքի կրիտիկական երկարություն[խմբագրել | խմբագրել կոդը]
Ալիքատարում ալիքի կրիտիկական երկարությունը վերին սահմանն է, որի դեպքում էներգիան տարածվում է ալիքատարում։ Ուղղանկյուն ալիքատարի համար ալիքի կրիտիկական երկարությունը որոշվում է
բանաձևով, որտեղ a-ն և b-ն ալիքատարի լայնական հատույթի չափերն են, m-ը և n-ը՝ դրանց վրա տեղավորվող կիսաալիքների թիվը[1], ε-ը՝ ալիքատարի միջավայրի դիէլեկտրիկ, μ-ն՝ մագնիսական թափանցելիությունները։
Բնութագրական դիմադրություն[խմբագրել | խմբագրել կոդը]
Բնութագրական դիմադրությունը ալիքային պրոցեսի էլեկտրական բնութագրի և մագնիսական բնութագրի հարաբերությունն է։ Տեղաբաշխված պարամետրերով գծերի տեսության մեջ բնութագրային դիմադրությունը՝
,
ուր և -ն վազող ալիքի լարման և հոսանքի կոմպլեքս ամպլիտուդներն են։ Հարթ էլեկտրամագնիսական ալիքների միջավայրի բնութագրային դիմադրությունը՝
:
Ալիքատարների տեսությունում այն որոշվում է որպես և վեկտորների լայնակի բաղադրիչների հարաբերություն.
:
Դիտարկենք առանձին E և H տիպի ալիքները։
1. E տիպի ալիք: Ձևափոխման բանաձևից ստանում ենք.
, :
այստեղից`
:
օգտագործելով.
,
կստանանք.
:
W - ալիքատարում պարունակող միջավայրի բնութագրական դիմադրություն.
2. H տիպի ալիք:
Նույնանման գործողություններ կատարելով՝ կստանանք.
:
Հոսանքը ալիքատարի պատերին[խմբագրել | խմբագրել կոդը]
Քանի որ մակերեսային հոսանքի խտությունը ալիքատարի իդեալական հաղորդիչ պատերին հավասար է,
- ,
ապա հոսանքի ուժագծերի պատկերը ալիքատարի պատերին կներկայացնի մագնիսական դաշտի ուժագծերին օրթոգոնալ կորերի համայնք (տես նկ.1-ում)։ Նշենք, որ այստեղ տրված է հոսանքների բաշխման ակնթարթային պատկերը։ Ժամանակային առումով այն տեղափոխվում է որպես միասնություն V արագությամբ։ Ակնհայտ է, որ հոսանքի ուժագծերը միշտ փակ են։
Ալիքատարային տեխնիկայում ճեղք են կոչում ուղղանկյուն բացվածքը ալիքատարի պատին, ընդ որում ճեղքի երկարությունը գերազանցում է նրա լայնությունը։ Ենթադրենք, ալիքատարի նեղ պատին երկու ճեղք է արված, որոնցի մեկը կողմնորաշված է առանցքային ուղղությամբ, իսկ երկրորդը լայնակի ուղղությամբ։ Առաջինը մակերեսային հոսանքի գծերը հատում է 90 անկյան տակ։ ճեղքի ներքեւի եզրին մոտեցող հոսանքը այստեղ կստեղծի դրական լիցք։ Վերեւի եզրին կկուտակվի արժեքով հավասար բացասական լիցք։ ժամանակի ընթացքում այդ լիցքերը կփոխվեն ըստ գեներատորի տատանումների։ Այդպիսի ճեղքը՝ էլեկտրամագնիսական ալիքներ ճառագայթիչ է։ Մյուս ճեղքը, որն արված է հոսանքի գծերին զուգահեռ, իր նեղության պատճառով եզրերին լիցքեր չի կուտակի եւ չի ճառագայթի։ Այսպիսով, ալիքատարի պատին ճեղքը ճառագայթում է այն դեպքում եթե այն հատում է հոսանքի ուժագծերը։
Մետաղյա ալիքատարներում ալիքների մարումը[խմբագրել | խմբագրել կոդը]
Գործնականում այս կամ այն հաղորդման գիծն ընտրելիս, օրինակ, ալիքատարային կապի երկար գծերը ստեղծելիս, որոշիչ բնութագիր է ծառայում մարումը, այսինքն՝ ալիքատարում կորուստների չափը։
Սնամեջ մետաղյա ալիքատարում էներգիայի կորուստի պատճառներից են.
1) պատերի նյութերի որոշակի ոչ անվերջ հաղորդականությունը,
2) ալիքատարի միջի դիէլեկտրիկով հոսող հաղորդման հոսանքները (քանի որ դիէլեկտրիկը իդեալական չէ)։
Էլեկտրամագնիսական դաշտերի ամպլիտուդները կորուստներով ալիքատարում նվազում են էքսպոնենտի օրենքով ալիքատարի երկայնքով։
Համարելով երկայնակի ալիքատարի թիվը կոմպլեքս մեծություն, կստանանք.
,
այստեղ -փուլային հաստատւնն է, -ը՝ մարման հաստատունը։
Ռեգուլյար հաղորդման գծերում կորուստն ընդունված է բնութագրել միավոր երկարության գծում մարման միջոցով։ Ենթադրենք, 1մ երկարությամբ ալիքատարի կտորում մուտքի էլեկտրական լարվածությունը է, իսկ ելքում՝ :
Նեպ/մ,
Ռադիոտեխնիկայում միավոր երկարության գծում մարումը հաճախ արտահայտում են դեցիբելով։
դԲ/մ,
Նեպերի և դեցիբելի կապը հետևյալն է.
(դԲ)(Նեպ) ։
ԳԲՀ տիրույթում ավելի հաճախ գործողությունները կատարվում են դաշտի հզորության հետ, քանի որ այն ավելի հեշտ է չափվում։ Քանի որ հզորությունը միշտ համեմատական է դաշտի լարվածության քառակուսուն, ապա՝
դԲ/մ։
Միավոր երկարության գծում մարման գործակիցը ուղղանկյուն մետաղյա ալիքատարում որոշվում է՝
դԲ/մ ,
Ալիքատարում ալիքների փուլային և խմբային արագությունը [խմբագրել | խմբագրել կոդը]
Օգտվելով բանաձևից հաշվարկենք սնամեջ մետաղյա ալիքատարում խմբային արագությունը։
Այստեղից ,
Ինչպես երևում է բանաձևից՝
1) Ալիքատարում ալիքների խմբային արագությունը միշտ փոքր || փուլային արագությունից եւ փոքր լույսի արագությունից։
2) Փուլային եւ խմբային արագությունները կապված են իրար`
VՓ . VԽ = c2
3) Ընտրված տիպի տատանումների կրիտիկական հաճախականությանը ձգտող միջին հաճախականությամբ ազդանշանների խմբային արագությունը ձգտում է զրոյի։ Միջին հաճախականության բարձրացման հետ խմբային արագությունը աճում է, ընդ որում հաճախականության վերին սահմանը դեպքում հավասար է :
VԽ - ի հաճախականությունից կախվածությունը ի հայտ է գալիս
ալիքատարային գծերով շատ կարճ ռադիոիմպուլսների հաղորդման պրոցեսը ուսումնասիրելիս։ Այդպիսի իմպուլսների սպեկտրը կարող | այնքան լայն լինել, որ արդեն չի կարելի ասել, որ ալիքատարի առանցքի երկայնքով ալիքների համընդհանուր խմբեր են գոյանում։ Լայնատիրույթ տատանումը ուսումնասիրելիս պետք է առանձնացնել խմբեր, որոնցից ամեն մեկը իր սեփական VԽ -յամբ է տարածվում։ Արդյունքում, ելքի
ազդանշանը ալիքատարի բավական երկար լինելու դեպքում աղավաղվում է։
Տիպերը[խմբագրել | խմբագրել կոդը]
Ըստ կառուցվածքի՝ ալիքատարները կարող են լինել ուղղանկյուն և կլոր։
Ուղղանկյուն մետաղյա ալիքատարը ուղղանկյուն հատույթ ունեցող խողովակ է, որը ծառայում է որպես հաղորդման գիծ։ Կլոր ալիքատարը r ներքին շառավիղով սնամեջ մետաղյա խողովակ է, որն անվերջ ձգված է իր երկայնքով ուղղված առանցքով։ Կլոր և ուղղանկյուն ալիքատարներում պատերի հաղորդականությունները համարվում են անվերջ մեծ, և ընդունում, որ ներսում վակուում է։ Գործնականում, այս կամ այս կամ այն հաղորդման գիծը ընտրելիս, օրինակ ալիքատարային կապի երկար գծերը ստեղծելիս, որոշիչ բնութագիր է ծառայում մարումը, այսինքն՝ ալիքատարում կորուստների չափը։ Սնամեջ մետաղյա ալիքատարում էներգիայի կորուստի պատճառներից են՝
- պատերի նյութերի որոշակի ոչ անվերջ հաղորդականությունը
- ալիքատարում պարունակվող դիէլէկտրիկով հոսող հաղորդման հոսանքներ (քանի որ դիէլէկտրիկը իդեալական չէ)։
Կլոր մետաղյա ալիքատար[խմբագրել | խմբագրել կոդը]
Կլոր մետաղյա ալիքատարը a ներքին շառավղով սնամեջ մետաղյա խողովակ է, որն անվերջ ձգված է z առանցքի երկայնքով։
՛
Կլոր ալիքատար
Ինչպես և ուղղանկյուն ալիքատարում, պատկերի հաղորդականությունը համարում ենք անվերջ մեծ, ալիքատարը՝ z առանցքով համասեռ և ընդունում, որ ներսում վակում է։Դիտարկենք էլեկտրական և մագնիսական տիպի ալիքների տարածումը այդպիսի համակարգում։
Դրված խնդիրը կարելի է լուծել, օգտագործելով ուղղանկյուն ալիքարտարի համար ստացված արդյունքները։Այդպես, մեզ հայտնի H10 տիպի ալիքի պատկերը ուղղանկյուն ալիքատարում կարող ենք վերածել կլոր ալիքատարում հիմնական ալիքի պատկերի՝ ուղղանկյուն հատույթը հաջորդաբար դեֆորմացիաների ենթարկելով։
 Դաշտի կառուցվածքը կլոր ալիքատարում
Դաշտի կառուցվածքը կլոր ալիքատարում
Սկզբունքորեն կարևոր է այն փաստը, որ էլեկտրական վեկտորի ուժագծերը միշտ ուղղահայաց են ալիքատարի մետաղյա պատերին։
Չնայած կոնստրուկտիվ և տեխնոլոգիական առավելությունների , կլոր ալիքատարը գործնականում ավելի հազվադեպ է կիրառում, քան ուղղանկյունը։Դա պայմանավորված է կլոր ալիքատարում H11 հիմնական տիպի ալիքի բևեռային անկայունությամբ։ Այն կլոր ալիքատարի սիմետրիկության հետևանքն է։ Օրինակ, եթե ալիքատարի մուտքում H11 ալիքը բևեռացված է այնպես , ինչպես նկարում է, ապա տրակտի տարբեր պատահական և միտումնավոր դեֆորմացիաների պատճառով կստանանք ուրիշ ողղությամբ բևեռացման հարթություն։ Հենց այդ պատճառով կլոր ալիքատարը հաճախ չի կիրառվում որպես հաղորդման գիծ։
 Բևեռացման ուղղության փոփոխություն
Բևեռացման ուղղության փոփոխություն
Դրա հետ մեկտեղ, անկյունային կրդինատով կլոր ալիքատարի սիմետրիկության երևույթը օգտակար է ֆերիտային ալիքատարային ԳԲՀ սարքավորումներում, պտտվող անդամակցումներում և այլն։
Նկարում բերված է մակերեսային հոսանքների բաշխումը կլոր ալիքատարում H10 տիպի ալիքի տարածման դեպքում։

Կլոր ալիքատրներում միավոր երկարության գծում մարման գործակիցը որոշվում է հետևյալ բանաձևով ․
դԲ/մ ,
Մանրաթելա օպտիկական հաղորդման գծեր[խմբագրել | խմբագրել կոդը]
Քսաներրդ դարի վերջին տասնամյակը բնութագրվում է էլեկտրոնիկայի, հաշվիչ տեխնիկայի կտրուկ զարգացմամբ, որի շնորհիվ առաջ եկան Internet E-mail և այլ ծառայություններ։ Այս ծառայությունների արագագործության բարձրացման նպատակով ( մինչեւ մի քանի Tbit/sec) վերջին տարիներին լայն տարածում են ստացել մանրաթելա-Օպտիկական կապի գծերը (ՄՕԿԳ)։
ՄՕԿԳ-ի առավելություններն են.
• արտաքին էլեկտրամագնիսական ազդեցությունից պաշտպանվածությունը
• կայունություն քիմիական ազդեցության նկատմամբ
• փոքր չափսերը (d2+jacket=250մկմ) և զանգվածը
• Մեծ թողունակություն
• Փոքր կորուստները
ՄՕԿԳ -ի աշխատանքի սկզբունքը ճիշտ պատկերացնելու համար անհրաժեշտ է ծանոթանալ օպտիկայում հայտնի Սնելիուսի օրենքներին։
Երբ ճառագայթը հասնում է երկու թափանցիկ միջավայրերի հարթ սահմանին, ապա այն մասամբ անցնում է երկրորդ միջավայր ( բեկվում է), իսկ մասամբ` անդրադառնում։ Ընդ որում, միեւնույն հարթության մեջ գտնվող ընկնող եւ անդրադարձող ճառագայթների անկյունները իրար հավասար են։
Բեկված ճառագայթը նույնպես գտնվում է ընկնող ճառագայթի հետ մեկ հարթության մեջ, ընդ որում ընկնող եւ բեկված ճառագայթների նորմալի հետ կազմած անկյունների սինուսների հարաբերությունները հակադարձ համեմատական են նրանց բեկման ցուցիչների հարաբերությանը։
Եթե n1 > n2, ապա X < Z :
Եթե n1 < n2, ապա X > Z :
Եթե n1 = n2, ապա ասում են, որ տեղի ունի ուղղագիծ տարածում։
Օպտիկական մանրաթելը աշխատում է տեսանելի լույսի տիրույթում (0.38.0.78) մկմ։ Օպտիկական ճառագայթը ընկնում է
մանրաթելի լավ հղկված մակերեսի վրա a0 անկյան տակ։ Այնուհետև
այն բեկվում է եւ անցնում n1 բեկման ցուցիչ ունեցող միջավայրը, հասնում է միջուկին a1 , անկյան տակ։ Այստեղ գործում է Սնելիուսի
օրենքը` n0 sin(a0 ) = n1 sin(a1 ): Հանդիպելով միջուկ - պատյան սահմանագծին b անկյան տակ, ճառագայթը բեկվելով դուրս է գալիս պատյան a2, անկյան տակ n1 sin( b) = n2 sin(a2 ):
Կիրառությունները[խմբագրել | խմբագրել կոդը]
| Այս հոդվածը կամ բաժինը կարող է չհամապատասխանել հանրագիտական ոճի վերաբերյալ Վիքիպեդիայի չափանիշներին: Ներկայացված մտահոգությունների համար այցելեք քննարկման էջը: Տե՛ս Վիքիպեդիայի ոճական ուղեցույցը հոդվածը բարելավելու ցուցումների համար: |
Ալիքատարները կիրառվում են 50սմ-ից 1մմ ալիքի երկարության տիրույթներում։ Դեցիմետրային տիրույթում, որպես հաղորդման գծեր, ալիքատարները օգտագործվում են միայն բարձր հզորության սարքերում, իսկ սկսած մոտ 6սմ ալիքի երկարությունից՝ կիրառվում են ամենուր։ Սնամեջ մետաղյա ալիքատարների լայն կիրառությունը պայմանավորված է դրանց մի շարք առավելություններով. ալիքատարային կոնստրուկցիաները տեխնոլոգիապես շատ են հարմար, մարումը ցածր է, կա մեծագույն իմպուլսային հզորություններ հաղորդելու հնարավորություն։ Ռադիոհաճախային էլեկտրական ալիքատարերը մշտապես օգտագործվում են ռադիոլոկացիոն կայաններում, արագացուցիչներում։ Ձայնային ալիքատարերը օգտագործվում են նավերում, կրկնօրինակելով էլեկտրոնային խոսակցական մեխանիզմները նրանց խափանման ժամանակ։
Ուղղանկյուն մետաղյա ալիքատարը ուղղանկյուն հատույթ ունեցող խողովակ է, որը ծառայում է որպես հաղորդման գիծ։ Հատույթի լայն պատի չափը նշանակենք a,իսկ նեղ պատինը՝b: z առանցքի ուղղությամբ, որով տարածվում են էլեկտրամագնիսական ալիքները, ալիքարատը անվերջ երկար ենք համարում(նկ.1)։Ենթադրենք նաև, որ ալիքատարի ներսում օդ է կամ վակուում, այսինքն՝ մի նյութ, որի εa=ε0,µa=µ0 : Գործնականում հենց այդպես էլ լինում է։ Ալիքատարի պատերը համարվում են իդեալական հաղորդիչ, այսինքն՝ պատրաստվում են σ=∞ տեսակարար ծավալային հաղորդականությամբ նյութից։ Այսպիսով, ալիքատարում կորուստներ չկան։

a-ի և b-ի արժեքները ընդհանուր առմամբ չափվում է միլիմետրերով։ Առավել տարածված են 23х10 մմ և 8х16 մմ չափերով ՈՒԱ-ները։ ՈՒԱ-ների հիմնական հատկությունները, որոնց հետևանքով նրանք լայն կիրառություն ունեն ԳԲՀ տեխնիկայում, հետևյալն են. 1.Ամբողջական պաշտպանություն, քանի որ ՈՒԱ-ները հանդիսանում են փակ կառույց, այդ դեպքում արտաքին դաշտը չի թափանցում ներս և ՈՒԱ-ում տարածվող ալիքների դաշտը ոչ մի կերպ չի ազդում շրջապատող առարկանների վրա; 2.Ալիքների քիչ մարում; 3.Հզորության բարձր արժեք, որը ՈՒԱ-ն դարձնում է անփոխարինելի( ռադարային կայաններում և այլուր)։ ՈՒԱ-ի թերությունը այն է, որ նա պետք է ունենա մեծ զանգված և չափեր, որոնք սահմանափակում են ՈՒԱ-ների օգտագործումը երկրի արհեստական արբանյակների և այլ տիեզերական սարքավորումների մեջ։ Չնայած, ժամանակակից տեխնոլոգիաները թույլ են տալիս պատրաստել ՈՒԱ-ներ պլաստիկից՝ ներքին մակերեսը արծաթի շերտով պատելու միջոցով, որոնց շնորհիվ ՈՒԱ-ի զանգվածը զգալիորեն փոքրանում է։
Սեփական ալիքներ են անվանում ազատ ներդաշնակ էլեկտրամագնիսական ալիքները իդեալական պատերով ՈՒԱ-ում։ Եվ ՈՒԱ-ն լցված է դիէլեկտրկով՝ առանց կորուստների։
ՈՒԱ սեփական ալիքների դաշտերը սահմանելու համար անհրաժեշտ է որոշել Հելմհոլցի համասեռ հավասարումը՝ կապված էլեկտրական Ėm և մագիսական Ḣm դաշտերի լարվածությունների կոմպլեքս ամպլիտուդների հետ. ΔĖm+k2 Ėm=0 (1) ΔḢm+k2 Ḣm=0 Սահմանային պայմանների դեպքում՝ իդեալական պատերով ալիքատարում. Ėmτ=0 Ḣmʟ =0 (2)
որտեղ k – ն ալիքային թիվն է ազատ տարածությունում-k=ω/c; Ėmτ և Ḣmʟ - էլեկտրական և մագնիսական դաշտի լարվածության կոմպլեքս ամպլիտուդների տանգենցյալ և նորամալ բաղադրիչներն են։ (1)-(2) լուծուներով կարելի է ներկայացնել Օz առանցքի երկայնքով տարածվող ալիքների տեսքը. Ėm(x,y,z)=Ėm(x,y)e-ißz (3) Ḣm (x,y,z)= Ḣm (x,y)e-ißz
Ėm(x,y) և Ḣm (x,y) ֆունկցիաները նկարագրում են ՈՒԱ-ի լայնակի հատույթով դաշտի բաշխումը։ Տեղադրելով(5.3)-ը (5.1)-ի մեջ, ստանում ենք երկչափ հավասարում այդ ֆունկցիաների գտնելու համար. ΔʟĖm+k2 Ėm=0 (4) ΔʟḢm+k2 Ḣm=0 kʟ2= k2-ß2- լայնակի ալիքային թիվ։ (4) վեկտորական հավասարումը վերածենք սկալյար հավասարման Ėm(x,y) և Ḣm (x,y) դաշտերի x,y և z բաղադրիչների համար, այսինքն ՈՒԱ սեփական ալիքի դաշտի գտնելը հանգեցնում է Հելմհոլցի 6 սկալյար հավասարումների լուծմանը՝ ՈՒԱ լայնակի կտրվածքում։ Սահմանային պայմաններին բավարարելու համար անհրաժեշտ է իմանալ իդեալական հաղորդիչ պատերի վրա լիցքերի և հոսանքի բաշխվածությունը, որը մեզ նախօրոք հայտի չէ։ Այդ իսկ պատճառով սկալյար հավասարումների լուծումը կարելի է ստանալ միայն Emz և Hmz դաշտերի երկայնակի բաղադրիչների համար, քանի որ նրանք բավարարում են պարզ պայմանների. Emz=0,∂Hmz∕∂n=0
Որտեղ- ∂ ∕ ∂n ածանցյալն է ըստ ալիքատարի պատի նորմալի։
Հեշտ է համոզվել, որ երկայնակի բաղադրիչի համար ներկայացված խնդիրները ունեն 0-ական լուծուներ՝ Emz=0 և Hmz=0:Սրա հիման վրա տարբերում ենք ՈՒԱ սեփական ալիքների 2 տեսակ՝ E-ալիքներ, որը ՈՒԱ սեփական այն ալիքներն են, որոնք ունեն էլեկտրական դաշտի լայնակի բաղադրիչ, իսկ Hz=0: H-ալիքներ, որոնք ՈՒԱ սեփական այն ալիքներն են, որոնք ունեն երկայնակի՝Hz բաղադրիչ, իսկ Ez=0: E-ալիքներին անվանում են նաև էլեկտրական կամ լայնակի-մագնիսական ալիքներ (ТМ-ալիքներ)։ Н-ալիքներին համապատասխանաբար անվանում են մագնիսական կամ լայնակի-էլեկտրական։ Երկրորդ անվանումը արտահայտում է այն փաստը, որ Е-(Н-) ալիքների մագնիսական (էլեկտրական) դաշտի վեկտրները ընկած են ՈՒԱ լայնակի կտրվածքի հարթության մեջ ( z=const նկար 1-ում)։ ՈՒԱ սեփական ալիքները, որոնցում Ez≠0 և Hz≠0 կարելի է ներկայացնել E - և H-ալիքների վերադրման տեսքով։ Այդպիսի ալիքներին անվանում են հիբրիդային։ Դաշտի լայնակի բաղադրիչները. Ėmτ=x0 Ėmx +y0 Ėmy Ḣmτ=x0Ḣmx+y0Ḣmy
Եվ այսպես, ՈՒԱ սեփական ալիքի դաշտի հաշվարկը հանգեցնում է 2 խնդիրների լուծմանը. E-ալիքներ ∆ʟEmz+ kʟ2Emz=0 (6) Emz=0 պատերին H-ալիքներ ∆ʟHmz+ kʟ2Hmz=0 (7) ∂Hmz∕∂n=0 պատերին
Օգտագործելով փոփոխականների բաժանման մեթոդը, հեշտ է ստանալ(6)-ի և (7)-ի լուծումները, սահմանային պայմաններին բավարարման դեպքում x=(0; a) և y=(0; b) (նկար 1)։ Ėmz= Ė0sin(nπx∕a)sin(mπy∕b) (8) Ḣmz=Ḣ0cos(nπx∕a)cos (mπy∕b) որտեղ Ė0 և Ḣ0 հանդիսանում են դաշտի ամպլիտուդները։ n և m – ամբողջ թվեր են։ Դաշտի մնացած բաղադրիչները որոշվում են դիֆերենցելով Emz կամ Hmz ՝համաձայն (5)-ի։ Յուրաքանչյուր ամբողջ թվային զույգին համապատասխանում է ՈՒԱ դաշտի իր բաժանումը, այսինքն (n,m) հավաքածուն որոշում է ալիքատարում սեփական ալիքի տիպը։ Այլ խոսքով, գոյություն ունեն բազմաթիվ E- և H-տիպի ալիքներ։ Նրանց համար ընդունել ենք հետևյալ նշանակումը՝ Enm և Hnm:Պատկեր:Ուղղ,ալիքատար.jpg
(8)-ից հետևում է, որ E-ալիքների համար Ėmz= 0,երբ n=0 կամ m=0: Այդ կերպ, Enm ալիքները գոյություն ունեն միայն n և m>0 դեպքում։ H –ալիքների համար, երբ n=m=0՝ Ḣmz =const, այդ դեպքում Ėmt= 0, Ḣmt =0: Հետևաբար, H00 ալիքներ գոյություն չունեն։Բայց այդ ինդեքսներից որևէ մեկը (n կամ m)կարող է հավասար լինել 0-ի, այսինքն հնարավոր ալիքների տիպեր են H0m և Hn0:
Որոշենք պայմաններ, ըստ որի a և b չափերով ՈՒԱ-ում կարող են տարածվել տվյալ հաճախությամբ ալիքի տիպ։ Ինչպես նշված է վերևում, ալիքատարում տարածվող ալիք կարող է գոյություն ունենալ հետևյալ անհավասարությանը բավարարելու դեպքում՝ k>kլ, այսինքն. K= 𝞈∕c> kʟ=((nπ/a)2+(mπ/b)2)1/2:
Այդ դեպքում հաճախությունը պետք է բավարարի հետևյալ անհավասարությանը՝ 𝞈< 𝞈կր, որտեղ
𝞈կր =c((nπ/a)2+(mπ/b)2)1/2:
𝞈կր տվյալ տիպի ալիքի կրիտիկական հաճախություն։ 𝞈< 𝞈կր դեպքում (n, m) ինդեքսներով ալիքը տարածվել չի կարող։ Կրիտիկական հաճախությունը աճում է n և m ինդեքսների աճի հետ մեկտեղ։ Մինիմալ 𝞈կր ունեցող ալիքը անվանում են հիմնական ալիք (հիմնական տիպի ալիք)։ Մնացած ալիքներին անվանում են բարձր կարգի ալիքներ։ Քանի որ a –ն երկար պատի չափն է, ապա 𝞈կր–ի արտահայտությունից հետևում է, որ ՈՒԱ հիմնական ալիքների մոտ՝n=1, m=0: Պարզ է, որ այդ H-ալիքը H10-ն է, քանի որ E-տիպի ալիքի m>0: H10-ի կրիտիկական հաճախությունը,𝞈կր (H10)=cπ/a=>fկր(H10)=𝞈կր/2π=c/2a:
Ալիքատարի տեսության մեջ օգտագործվում է նաև ալիքի կրիտիկական երկարություն հասկացությունը, և համապատասխանաբար ազատ տարածության կրիտիկական հաճախություն՝λկր=c/fկր։ H10 Ալիքների համար λկր=2a - հավասար է ՈՒԱ լայն պատի երկարության կրկնապատիկին։
Հիմանական ալիքի կրիտիկական հաճախությունից փոքր հաճախությունների դեպքում ՈՒԱ-ում ալիքային պրոցես տեղի չի ունենում։ Տվյալ իրավիճակում ալիքատարին անվանում են սահմաններից դուրս գտնվող։ Այդպիսի ալիքատարը ներկայացնում է անվերջ թվով մարող ալիքների վերադրում (8), համապատասխանաբար տարբեր մարման գործակիցներ.
αmn=((nπ/a)2+(mπ/b)2-k2)1/2 (10)։ 
Ալիքատարում ալիքի երկարությունը որոշվում է հետևյալ արտահայտությամբ՝λ=2π/ß: Այս արտահայտության մեջ տեղադրելով ß-ն, կստանանք.
λ=λ/(1-(λ/ λկր))1/2
Նշենք հետևյալ առանձնահատկությունները.
1.Ալիքատարում ալիքր երկարությունը մեծ է ազատ տարածության ալիքի երկարությունից ՝λ=c/f ալիքի միևնույն հաճախության դեպքում;
2.Երբf→fկր, λ→∞ - դաշտը մոտենում է սինֆազին; 
f>>fկր, ապա λ≈c/f=λ, այսինքն ալիքատարում ալիքի երկարությանը հաճախության մեծացման դեպքում մոտենում է ազատ տարածության ալիքի երկարությանը – նկ. 3:
Ալիքի գծային արտահայտությունից կարելի է ստանալ բանաձև ՈՒԱ սեփական ալիքի փուլային արագության հաշվարկի համար. νnm=𝞈 ∕ ß=𝞈 ∕ 2π λ=c/(1-(fկր/f)2)1/2: ՈՒԱ սեփական ալիքների փուլային արագությունը մեծ է լույսի արագությունից, այդ իսկ պատճառով ՈՒԱ սեփական ալիքներին անվանում են արագ ալիքներ։ ՈՒԱ սեփական ալիքի խմբային արագությունը (էներգիայի տարածման արագությունը) չի համընկնում փուլի հետ. νխմբ=d𝞈∕dß= c/(1-(fկր/f)2)1/2: Խմբային արագությունը փոքր է լույսի արագությունից, f=f,vгр=0 ,այսինքն ալիքային պրոցեսը վերանում է։ Նշենք որ, vгр և vnm կախված են հաճախությունից, հետևաբար ՈՒԱ առաջանում է դիսպերսիա։ Մեծ հաճախությունների դեպքում , խմբային և փուլային արագությունները ալիքատարում լցված դիէլեկտրիկում ձգտում են լույսի արագությանը։ Փուլային արագության ձգտելը անվերջության f→fկր դեպքում, պայմանավորված է նրանով, որ երբ f<fկր ՈՒԱ-ում տատանումները դառնում են սինֆազ։
Իրական ալիքատարներում տեղի է ունենում էլեկտրամագնիսական էներգիայի կորուստ, ինչի արդյունքում էլ նկատվում է ալիքների մարում։ Այս պրոցեսը բնութագրվում է կորուստների գծային հզորությունը։

Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ «Ալիքատարների կրիտիկական չափերը». Արխիվացված է օրիգինալից 2016 թ․ մարտի 5-ին. Վերցված է 2014 թ․ դեկտեմբերի 22-ին.
Գրականություն[խմբագրել | խմբագրել կոդը]
- Ա. Սարգսյան, Էլեկտրադինամիկա և ռադիոալիքների տարածում։ Ուսումնական ձեռնարկ։ Հայաստանի Պետական Ճարտարագիտական համալսարան, Երևան, 2004, 170 էջ։
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- The Feynman Lectures on Physics Vol. II Ch. 24: Waveguides
- Միկրոալիքները ալիքատարներում(չաշխատող հղում) (անգլ.)
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Ալիքատար» հոդվածին։ |
|
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 1, էջ 176)։ |


















![{\displaystyle {\vec {j_{s}}}={\Bigl [}{\vec {i_{n}}}\mathrm {X} {\vec {H}}{\Bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/189eaa498e969d7d2166d61ad27bc42418b78783)












![{\displaystyle \alpha _{m}={8,69{\sqrt {\omega \mu _{0} \over 2\sigma }}[1+{2b \over a}{\Bigl (}{\lambda _{0} \over 2a}{\Bigr )}^{2}] \over 120\pi b{\sqrt {1-{\Bigl (}{\lambda _{0} \over 2a}{\Bigr )}^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ca0d3e1fb4dd25aee772074676614d887b97484)









