Ժամանակի դանդաղում

Ժամանակի դանդաղում, հարաբերականության տեսությունում իրադարձությունների ժամանակների տարբերությունը, որը չափում են միմյանց հանդեպ շարժման մեջ գտնվող դիտորդները։
Մի դիտորդի նկատմամբ դադարի վիճակում գտնվող ճշգրիտ ժամացույցը երկրորդ դիտորդի նույնչափ ճշգրիտ ժամացույցի հետ համեմատած կարող է ընթանալ այլ արագությամբ։ Այս էֆեկտը չի առաջանում ժամացույցներով պայմանավորված տեխնիկական պատճառներից կամ այն փաստից, որ ազդանշանի տարածվելու համար ժամանակ է պահանջվում, այլ հենց տարածաժամանակի բնույթով։
Նկարագրություն[խմբագրել | խմբագրել կոդը]
Սփեյս Շաթլի ժամացույցները ավելի դանդաղ են շարժվում, քան Երկրի վրա գտնվող ժամացույցները, մինչդեռ գլոբալ տեղորոշման համակարգի և Գալիլեյ արբանյակային տեղորոշման համակարգի արբանյակները մի քիչ ավելի արագ են ընթանում[1]։ Այսպիսի ժամանակային դանդաղումները բազմիցս ի ցույց են դրվել, օրինակ, Երկրի վրա և տիեզերքում անխափան աշխատող ատոմային ժամացույցների ցուցմունքների տարբերություններով։ Բնության օրենքներն այնպիսին են, որ ժամանակն ինքնին (այսինքն՝ տարածաժամանակը) կորանում է գրավիտացիայի կամ արագության տարբերությունների պատճառով․ դրանցից յուրաքանչյուրը ժամանակի վրա տարբեր ձևով է ազդում[2][3]։
Ժամանակի դանդաղումը կարող է ազդել առաջատար տեխնոլոգիաներ և մեծ արագությունների հնարավորություններ ունեցող տիեզերագնացների նախատեսված հանդիպման վրա։ Տիեզերագնացները կարող են իրենց ժամացույցները կարգաբերել ճիշտ 80 տարվա համար, մինչդեռ Երկրի համար այդ տևողությունը կարող է լինել 81 տարի։ Տիեզերագնացները կարող են վերադառնալ Երկիր՝ մեկ տարով պակաս մեծացած լինելով, քան Երկրի վրայի մարդիկ։ Ժամանակի տեղային ընկալումը որևէ մեկի համար երբեք չի փոխվում։ Այլ կերպ ասած, տիեզերագնացները և Երկրի վրայի անձնակազմը, չնայած ժամանակի հապաղման էֆեկտին, իրենց սովորականի պես են զգում։
Այս տարբերությունները աննշան են, քանի որ սահմանափակված են տիեզերագնացների արագություններով. Միջազգային տիեզերական կայանում 6 ամիս անցկացնելուց հետո անձնակազմը Երկրի բնակիչների համեմատ ընդամենը մոտ 0,005 վայրկյանով պակաս է մեծանում։ Էֆեկտներն ավելի զգալի կլինեն, եթե տիեզերագնացները Միջազգային տիեզերական կայանի արագության փոխարեն, որը մոտ 7 700 մ/վ է, ճամփորդեն լույսի արագությանը մոտ արագությամբ (299 792 458 մ/վ)[4]։
Ժամանակի հապաղման պատճառը կա՛մ գրավիտացիայի, կա՛մ հարաբերական արագության տարբերությունների պատճառով է։ Միջազգային տիեզերական կայանի դեպքում ժամանակը դանդաղում է ուղեծրային արագության պատճառով։ Այս էֆեկտը թեթևակի նվազում է գրավիտացիոն պոտենցիալի ավելի փոքր արժեքի շնորհիվ։
Հարաբերական արագությամբ պայմանավորված ժամանակի դանդաղում[խմբագրել | խմբագրել կոդը]
Երբ երկու դիտորդներ հարաբերական շարժման մեջ են՝ գտնվելով որևէ գրավիտացիոն զանգվածի ազդեցության դաշտում, նրանցից յուրաքանչյուրի համար մյուսի (շարժվող) ժամացույցը ավելի դանդաղ կընթանա։ Որքան մեծ է հարաբերական արագությունը, այնքան մեծ է ժամանակի դանդաղումը։ Այս դեպքը երբեմն կոչվում է հատուկ հարաբերական ժամանակի դանդաղում։
Օրինակ, տիեզերքում իրար կողքով անցնող երկու հռթիռանավեր ժամանակի դանդաղում կունենան։ Եթե ինչ-որ կերպ մեկի անձնակազմը կարողանար հայտնվել մյուս նավում, կպարզեր, որ մյուսի ժամանակը և շարժումը դանդաղում է։ Այսինքն, առաջին նավի հաշվարկման համակարգում ամեն ինչ սովորականի պես է շարժվում, սակայն երկրորդ նավում թվում է, թե ամեն ինչ ավելի դանդաղ է շարժվում (և հակառակը)։
Տեղային տեսանկյունից ժամանակը, որը գրանցում են լոկալ հաշվարկման համակարգի նկատմամբ դադարի վիճակում գտնվող (և որևէ գրավիտացիոն զանգվածից հեռու) ժամացույցները, միշտ միևնույն արագությամբ է ընթանում։ Այլ կերպ ասած, եթե մի նոր, երրորդ նավ է շարժվում առաջինի երկայնքով, այն առաջին նավի համեմատ դադարի վիճակում է, և առաջին նավի տեսանկյունից ժամանակի ընթացքը երրորդում նորմալ կթվա[5]։
Հարց է առաջանում՝ եթե առաջին և երկրորդ նավերում կարծում են, որ մյուսում ժամանակը դանդաղ է ընթանում, ո՞վ ավելի մեծացած կլինի, եթե նրանք հանդիպեն։ Հարաբերական արագությամբ պայմանավորված ժամանակի դանդաղումը ավելի լավ հասկանալու դեպքում թվում է, որ երկվորյակների պարադոքսը ամենևին էլ պարադոքս չէ (պարադոքսի լուծումը ներառում է ժամանակային թռիչք, որի պատճառը դիտորդի՝ արագացում հավաքելն է)։ Նմանապես, երկվորյակների պարադոքսը հասկանալը կօգնի բացատրել, թե ինչու Միջազգային տիեզերական կայանի տիեզերագնացները ավելի դանդաղ են մեծանում (մոտ 0,007 վայրկյան՝ ամեն 6 ամսում), եթե նույնիսկ նրանք հարաբերական արագությամբ պայմանավորված ժամանակի դանդաղման են ենթարկվում։
Ժամանակի գրավիտացիոն դանդաղում[խմբագրել | խմբագրել կոդը]

Միջազգային տիեզերական կայանի տիեզերագնացների համար գործում է նաև ժամանակի գրավիտացիոն դանդաղումը, որը հակառակ ազդեցություն ունի հարաբերական արագությամբ պայմանավորված ժամանակի դանդաղման վրա։ Հարաբերական արագությունը և գրավիտացիան իրենց աճին զուգընթաց դանդաղեցնում են ժամանակը։ Տիեզերագնացների աճող արագությունը դանդաղեցնում է իրենց ժամանակը, մինչդեռ գրավիտացիան նվազում է՝ արագացնելով ժամանակի ընթացքը (տիեզերագնացներն ավելի փոքր գրավիտացիայի են ենթարկվում, քան Երկրի վրա է)։ Այնուամենայնիվ, ՄՏԿ տիեզերագնացները ի վերջո ժամանակի դանդաղման են ենթարկվում, քանի որ երկու հակառակ էֆեկտները հավասարաչափ ուժեղ չեն։ Արագությամբ պայմանավորված՝ ժամանակի դանդաղումն ավելի մեծ է, ինչի արդյունքում ժամանակը դանդաղում է։ Ժամանակը արագացնող էֆեկտները, որոնք պայմանավորված են փոքր գրավիտացիայով, չեն վերացնի արագությամբ պայմանավորված ժամանակի դանդաղումը, մինչև ՄՏԿ-ի ուղեծիրը Երկրից բավականաչափ հեռու չլինի։
Պատճառն այն է, որ երկու դիտորդները տարբեր հեռավորություններ ունեն մեծ գրավիտացիոն զանգվածից։ Հարաբերականության ընդհանուր տեսությունը նկարագրում է, թե ինչու գրավիտացիոն զանգվածին ավելի մոտ գտնվող ժամացույցի ընթացքը ավելի է դանդաղ թվում, քան զանգվածից ավելի հեռու գտնվող ժամացույցի ընթացքը։ Այս էֆեկտը չի տարածվում միայն տիեզերքում գտնվող տիեզերագնացների վրա. լեռնագնացի համար ժամանակը լեռան գագաթին ավելի արագ է ընթանում, քան ծովի մակարդակին մոտ գտնվողների համար։ Ժամանակի դանդաղման երկու դեպքերում էլ ժամանակի տեղային ընկալումը նորմալ է (ոչ ոք տարբերություն չի նկատում հենց իր հաշվարկման համակարգում)։ Արագությամբ պայմանավորված ժամանակի դանդաղման դեպքում երկու դիտորդներն էլ մյուսի շարժումը ավելի դանդաղ են տեսնում (փոխադարձ էֆեկտով)։ Ժամանակի գրավիտացիոն դանդաղման դեպքում երկու դիտորդները՝ թե՛ ծովի մակարդակին գտնվողը, թե՛ լեռնագնացը համաձայնում են, որ զանգվածին մոտիկ ժամացույցն ավելի դանդաղ է, և համաձայն են, որ ժամացույցների ցուցմունքները տարբեր են (այսպիսով ժամանակի գրավիտացիոն դանդաղումը փոխադարձ էֆեկտ չունի)։ Այսինքն՝ լեռնագնացը տեսնում է, որ ծովի մակարդակին գտնվող ժամացույցն ավելի դանդաղ է շարժվում, իսկ ծովի մակարդակին գտնվողները տեսնում են, որ լեռնագնացի ժամացույցն արագ է շարժվում։
Ժամանակի դանդաղումը հարաբերականության հատուկ և ընդհանուր տեսություններում[խմբագրել | խմբագրել կոդը]
Հարաբերականության տեսությունում ժամանակի դանդաղումը ընդհանրացվում է հետևյալ երկու իրավիճակների համար․
- Հարաբերականության հատուկ տեսությունում (կամ՝ հեռու որևէ գրավիտացիոն զանգվածից) իներցիալ հաշվարկման համակարգի նկատմամբ շարժվող ժամացույցները ավելի դանդաղ են ընթանում։ Այս էֆեկտը նկարագրվում է Լորենցի ձևափոխություններով։
- Հարաբերականության ընդհանուր տեսությունում ավելի փոքր գրավիտացիոն պոտենցիալի մոտ գտնվող ժամացույցները ավելի դանդաղ են ընթանում։
Հարաբերականության հատուկ և ընդհանուր տեսություններով պայմանավորված ժամանակի դանդաղման էֆեկտները կարող են միատեղ հանդես գալ (օրինակ՝ Միջազգային տիեզերական կայանի դեպքում)։
Հարաբերականության հատուկ տեսությունում ժամանակի դանդաղման էֆեկտը փոխադարձ է․ ինչպես դիտարկվեց իրար նկատմամբ շարժվող երկու ժամացույցներիկ համար, որոնք դիտման ընթացքում միմյանց հանդեպ արագացում ձեռք չեն բերում։ Ընդհակառակն, ժամանակի գրավիտացիոն դանդաղումը փոխադարձ չէ․ աշտարակի գագաթին գտնվող դիտորդը նկատում է, որ գետնին մոտ գտնվող ժամացույցն ավելի դանդաղ է, իսկ գետնին մոտ գտնվող դիտորդը կհամաձայնվի, որ տարբերություն կա։ Այնուհանդերձ ընկալումներում անհամաձայնությունը մնում է, քանի որ ամեն դիտորդ հավատում է, որ հենց ի՛ր ժամացույցն է ճիշտը, չնայած համաձայն է ժամանակի դանդաղման ուղղության և չափի համար։
Հարաբերական արագությամբ պայմանավորված ժամանակի դանդաղման մակաբերություն[խմբագրել | խմբագրել կոդը]
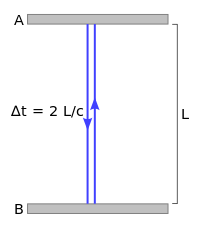

A․ Ներքևի հայելու դիրքը, երբ t'=0 պահին առաքվում է ազդանշանը:
B․ Վերևի հայելու դիրքը, երբ ազդանշանն անդրադառնում է t'=D/c պահին:
C․ Ներքևի հայելու դիրքը, երբ ազդանշանը հասնում է ներքև ժամանակի t'=2D/c պահին:
Ժամանակի դանդաղումը կարելի է մակաբերել բոլոր հաշվարկման համակարգերում լույսի արագության հաստատունության փաստի դիտարկումից[6][7][8][9]։
Լույսի արագության հաստատուն լինելը նշանակում է, որ նյութական մարմնի և լույսի արագությունները ադիտիվ չեն։ Հնարավոր չէ լույսի արագությունն ավելի մեծ դարձնել՝ ընթանալով դեպի լույսը ճառագայթող աղբյուրը։ Հնարավոր չէ լույսի արագությունն ավելի փոքր դարձնել՝ հեռանալով աղբյուրի հակառակ ուղղությամբ։
Պատկերացնենք A և B երկու հայելիներից կազմված պարզ ժամացույց։ Հայելիների միջև բաբախող լույս ունենք։ Հայելիների հեռավորությունը L է, ժամացույցը տկտկում է ամեն անգամ, երբ լույսը հասնում է տրված հայելուն։
Այն հաշվարկման համակարգում, որտեղ ժամացույցը դադարի վիճակում է (գծագիրը՝ աջից), լույսն անցնում է 2L ճանապարհ, իսկ ժամացույցի պարբերությունը 2L է՝ բաժանած լույսի արագության վրա՝
- :
Դադարի վիճակում գտնվող ժամացույցի հաշվարկման համակարգի նկատմամբ v արագությամբ շարժվող հաշվարկի համակարգում լույսն ավելի երկար, ճանապարհ է անցնում (անկյան տակ է շարժվում)։ Ըստ հարաբերականության հատուկ տեսության երկրորդ պոստուլատի՝ վակուումում լույսի արագությունը հաստատուն է բոլոր իներցիալ դիտորդների համար, ինչը նշանակում է, որ շարժվող դիտորդի տեսանկյունից ժամացույցի պարբերությունը մեծանում է։ Այսինքն՝ ժամացույցի նկատմամբ շարժվող հաշվարկման համակարգում ժամացույցն ավելի դանդաղ է ընթանում։ Կիրառելով Պյութագորասի թեորեմը՝ ստանում ենք հարաբերականության հատուկ տեսության հայտնի կանխատեսումները՝
Լույսի լրիվ ժամանակը հաշվում ենք
արտահայտությամբ։ Ունենալով տրված մեծությունները՝ հաշվում ենք կիսաճանապարհը․
- :
D-ն տեղադրելով նախորդ հավասարման մեջ և լուծելով Δt' -ի նկատմամբ, կստանանք
որտեղից, կիրառելով Δt-ի սահմանումը՝
- :
Այս արտահայտությունը ցույց է տալիս, որ շարժվող դիտորդի համար ժամացույցի պարբերությունն ավելի երկարատև է, քան ժամացույցի հաշվարկման համակարգում է։
Բանաձևի դիտարկում[խմբագրել | խմբագրել կոդը]
Հարաբերական արագության դեպք[խմբագրել | խմբագրել կոդը]

Հարաբերականության հատուկ տեսությունում ժամանակի դանդաղումը որոշվում է
բանաձևով, որտեղ Δt -ն որևէ իներցիալ համակարգում գտնվող դիտորդի տեսանկյունից ժամանակային ինտերվալն է նույն վայրում կատարվող երկու իրադարձությունների միջև (դիտորդի ժամացույցով) և կոչվում է սեփական ժամանակ, Δt′-ը ժամանակային ինտերվալն է այդ նույն իրադարձությունների միջև՝ չափված առաջին դիտորդի նկատմամբ v արագությամբ շարժվող մեկ այլ դիտորդի կողմից, v-ն դիտորդի և շարժվող ժամացույցի հարաբերական արագությունն է, c-ն լույսի արագությունն է, իսկ γ Լորենց-գործոնը՝
- :
Այսպիսով, շարժվող ժամացույցի ընթացքն աճում է․ այն դանդաղ է գործում։ Սովորական կյանքում, որտեղ v ≪ c, նույնիսկ տիեզերական ճամփորդությունների դեպքում այն բավարար չէ ժամանակի դանդաղման չափելի էֆեկտի համար, և կարելի է անտեսել այդպիսի չնչին էֆեկտը։ Միայն երբ մարմնի արագությունը մոտենում է լույսի արագության 1/10-ին՝ 30,000 կմ/վ, ժամանակի դանդաղումը կարևոր է դառնում։
Ժամանակի դանդաղումը Լորենց-գործոնով 1897 թվականին կանխատեսել է Ջոզեֆ Լարմորը միջուկի շուրջը պտտվող էլեկտրոնների համար։
Միաժամանակ գրավիտացիայով և շարժումով պայմանավորված ժամանակի դանդաղում[խմբագրել | խմբագրել կոդը]

Ժամանակի բարձր ճշգրտությամբ հաշվարկները, արբանյակային ցածր ուղեծրերի հետագծերի կազմումը պահանջում են հաշվի առնել շարժումով և զանգվածով պայմանավորված ժամանակի հապաղման երևույթները։ Գործնական օրինակներից է Միջազգային ատոմային ժամանակի ստանդարտը և դրա առնչությունները բարիցենտրիկ կոորդինատական ժամանակային ստանդարտին, որը կիրառվում է միջմոլորակային օբյեկտների համար։
Ժամանակի դանդաղման ռելյատիվիստական էֆեկտները Արեգակնային համակարգի և Երկրի համար կարելի է շատ ճշգրիտ մոդելավորել Այնշտայնի դաշտի հավասարումների Շվարցշիլդի լուծումով։ Շվարցշիլդի չափականությամբ dtE ինտերվալը տրվում է[11][12]
արտահայտությամբ, որտեղ
- dtE-ն tE սեփական ժամանակի փոքր աճն է (որը հնարավոր է հաշվել ատոմային ժամացույցով),
- dtc-ն tc կոորդինատի փոքր աճն է (կոորդինատային ժամանակ),
- dx, dy, dz-ը ժամացույցի դիրքի x, y, z կոորդինատների փոքր աճերն են,
- GM i/r i-ը՝ ժամացույցից r i հեռավորությունների վրա գտնվող զանգվածներով պայմանավորված նյուտոնյան պոտենցիալների գումարը։ Այս GM i/r i գումարը ներառում է մակընթացության և տեղեկատվության հետ կապված պոտենցիալները և ներկայացվում է որպես U (դրական աստղագիտական նշանով)։ Ժամացույցի կոորդինատային արագությունը տրվում է
արտահայտությամբ։
tc կոորդինատային ժամանակը այն ժամանակն է, որը ցույց կտա գրավիտացիոն զանգվածներից անվերջ հեռու գտնվող (U = 0) և կոորդինատական համակարգի նկատմամբ անշարժ (v = 0) հիպոթետիկ կոորդինատային ժամացույցը։ Արագության շառավղային բաղադրիչ ունեցող ժամացույցի համար ճշգրիտ առնչությունը սեփական ժամանակի ընթացքի և կոորդինատական ժամանակը ընթացքի միջև տրվում է
որտեղ
- v||-ն շառավղային արագությունն է,
- U = GM i/r i-ն՝ նյուտոնյան պոտենցիալը։
Հավասարումը ճիշտ է Շվարցշիլդի լուծման պայմանների դեպքում։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ 1,0 1,1 1,2 Ashby, Neil (2003). «Relativity in the Global Positioning System» (PDF). Living Reviews in Relativity. 6: 16. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. Արխիվացված է օրիգինալից (PDF) 2015 թ․ նոյեմբերի 5-ին. Վերցված է 2015 թ․ հոկտեմբերի 28-ին.
- ↑ Toothman, Jessika. «How Do Humans age in space?». HowStuffWorks. Վերցված է 2012 թ․ ապրիլի 24-ին.
- ↑ Lu, Ed. «Expedition 7 – Relativity». Ed's Musing from Space. ՆԱՍԱ. Արխիվացված է օրիգինալից 2016 թ․ հունվարի 19-ին. Վերցված է 2012 թ․ ապրիլի 24-ին.
- ↑ Lu, Ed. «Expedition 7 – Relativity». Ed's Musing from Space. ՆԱՍԱ. Արխիվացված է օրիգինալից 2016 թ․ հունվարի 19-ին. Վերցված է 2015 թ․ հունվարի 20-ին.
- ↑ Հատուկ հարաբերական ժամանակի հապաղման համար տես Ալբերտ Այնշտայնի հանրամատչելի բացատրությունը (անգլերեն հրատարակությունը՝ Einstein, Albert (1920). «On the Idea of Time in Physics». Relativity: The Special and General Theory. Henri Holt. ISBN 1-58734-092-5.)
- ↑ Cassidy, David C.; Holton, Gerald James; Rutherford, Floyd James (2002). Understanding Physics. Springer-Verlag. էջ 422. ISBN 0-387-98756-8.
- ↑ Cutner, Mark Leslie (2003). Astronomy, A Physical Perspective. Cambridge University Press. էջ 128. ISBN 0-521-82196-7.
- ↑ Lerner, Lawrence S. (1996). Physics for Scientists and Engineers, Volume 2. Jones and Bartlett. էջեր 1051–1052. ISBN 0-7637-0460-1.
- ↑ Ellis, George F. R.; Williams, Ruth M. (2000). Flat and Curved Space-times (2n ed.). Oxford University Press. էջեր 28–29. ISBN 0-19-850657-0.
- ↑ Ashby, Neil (2002). «Relativity in the Global Positioning System». Physics Today. 55 (5): 45. Bibcode:2002PhT....55e..41A. doi:10.1063/1.1485583.(չաշխատող հղում)
- ↑ Տես 2 և 3 հավասարումները Moyer, T. D. (1981). «Transformation from proper time on Earth to coordinate time in solar system barycentric space-time frame of reference». Celestial Mechanics. 23: 33–56. Bibcode:1981CeMec..23...33M. doi:10.1007/BF01228543.
- ↑ A version of the same relationship can also be seen at equation 2 in Ashbey, Neil (2002). «Relativity and the Global Positioning System» (PDF). Physics Today. 55 (5): 45. Bibcode:2002PhT....55e..41A. doi:10.1063/1.1485583. 35-36 էջերում։
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի օրվա հոդված: |











