Արագացում
| Արագացում | |
|---|---|
| Ընդհանուր սիմվոլներ | , |
| ՍԻ համակարգ | մ/վ2 |
| ՍԳՎ համակարգ | սմ/վ2 |
| Չափում LT−2 | |
| Դասական մեխանիկա |
|---|
| Դասական մեխանիկայի պատմություն · Դասական մեխանիկայի ժամանակացույց |
|
Ճյուղեր |
|
Հիմնական հասկացություններ Տարածություն · Ժամանակ · Արագություն · Արագացում · Զանգված · Ձգողություն · Ուժ · Իմպուլս · Իմպուլսի մոմենտ · Իներցիա · Իներցիայի մոմենտ · Էներգիա · Կինետիկ էներգիա · Պոտենցիալ էներգիա · Աշխատանք · Հզորություն |
|
Գիտնականներ |
Ֆիզիկայում արագացումը ժամանակի ընթացքում մարմնի արագության փոփոխման արագությունն է (ավելի հստակ ձևակերպմամբ՝ արագության առաջին կարգի ածանցյալը ըստ ժամանակի)։ Մարմնի արագացումը գումարային արդյունք է նրա վրա ազդող բոլոր ուժերի, ինչպես բնութագրվում է Նյուտոնի երկրորդ օրենքում[1]։ Միավորների միջազգային համակարգում արագացման չափման միավորը մ·վ−2-ն է (մ/վ2)։ Արագացումը վեկտորական մեծություն է՝ այն օժտված է ինչպես մեծությամբ, այնպես էլ ուղղությամբ, հետևապես արագացումները գումարվում են զուգահեռագծի կանոնով[2][3]։ Արագացումը սովորաբար նշանակվում է տառով (լատին․՝ acceleratio բառից), տեսական մեխանիկայում կարող է հանդիպել նաև նշանակումը[Ն 1]։ Մարմնի վրա ազդող արդյունարար ուժի (այսինքն՝ ազդող բոլոր ուժերի վեկտորական գումարի) վեկտորը ունի արագացման վեկտորի ուղղությունը, իսկ արդյունարար ուժի մեծությունը հավասար է մարմնի զանգվածի և արագացման մեծության արտադրյալին։
Օրինակ, Երկրի մակերևույթին մոտ (այսինքն՝ համեմատաբար փոքր բարձրությունների վրա) ուղղահայաց ազատ ընկնող մարմինը, օդի դիմադրությունը անտեսելու դեպքում, անկման յուրաքանչյուր վայրկյանում մեծացնում է իր արագությունը մոտավորապես 9,8 մ/վ-ով, այսինքն դա նշանակում է, որ ազատ անկման արագացումը հավասար է մոտ 9,8 մ/վ2-ու։
Եթե մեքենան սկսում է շարժումը դադարի վիճակից (այսինքն հաշվարկման իներցիալ համակարգում նրա սզբնական արագությունը զրո է), և շարժվում է ուղղագիծ՝ մեծացնելով արագությունը, ապա արագացման ուղղությունը կհամապատասխանի շարժման (այսինքն՝ արագության) ուղղությանը։ Այս դեպքում մեքենայի ուղևորները արագացումը ընկալում են որպես նստատեղին սեղմող ուժ։ Երբ մեքենայի արագությունը նվազում է, արագացման ուղղությունը հակառակ է արագության ուղղությանը, իսկ ուղևորները այն ընկալում են առաջ բրդող ուժի տեսքով[4]։ Եթե մեքենան շարժվի հաստատուն արագությամբ, արագացումը հավասար կլինի զրոյի։ Այն դեպքում, երբ մարմինը կատարում է հավասարաչափ շրջանագծային շարժում, այսինքն շարժվում է շրջանագծով՝ հաստատուն պահելով արագության մոդուլը, արագացումը հավասար չէ զրոյի․ մարմինն ունի մոդուլով հաստատուն, իսկ ուղղությամբ փոփոխական արագացում՝ ուղղված դեպի շրջանագծի կենտրոնը (կենտրոնաձիգ արագացում)։
Արագացումը նյութական կետի կինեմատիկայում[խմբագրել | խմբագրել կոդը]
Սահմանումը և հատկությունները[խմբագրել | խմբագրել կոդը]

Միջին արագացում[խմբագրել | խմբագրել կոդը]
Մարմնի միջին արագացումը սահմանվում է որպես ժամանակամիջոցի ընթացքում արագության փոփոխության և այդ ժամանակամիջոցի հարաբերություն՝
- ։
Ակնթարթային արագացում[խմբագրել | խմբագրել կոդը]
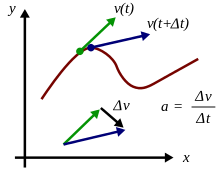
Ակնթարթային արագացումը միջին արագացման սահմանն է, երբ ժամանակամիջոցը ձգտում է զրոյի է՝ ։ Փաստորեն, մաթեմատիկական անալիզի տերմիններով՝ ակնթարթային արագացումը արագության առաջին կարգի ածանցյալն է ըստ ժամանակի

Դժվար չէ նկատել, որ արագացման ինտեգրալը արագությունն է՝ , որը համապատասխանում է կորի տակ ընկած պատկերի մակերեսին՝
- ։
Քանի որ արագացումը սահմանված է որպես արագության առաջին կարգի ածանցյալ ըստ ժամանակի, իսկ արագությունն իր հերթին՝ որպես շառավիղ-վեկտորի () առաջին կարգի ածանցյալ ըստ ժամանակի, ստացվում է, որ արագացումը շառավիղ-վեկտորի երկրորդ կարգի ածանցյալն է ըստ ժամանակի՝
- :
Այսպիսով, եթե նյութական կետի հետագծի վրա հայտնի են շառավիղ-վեկտորը և արագության վեկտորը ժամանակի որևէ պահին, ինչպես նաև արագացման կախումը ժամանակից, ապա, կարելի է լուծել հակադարձ խնդիրը․ ինտեգրելով այս հավասարումը, կարելի է ստանալ կետի կոորդինատները և արագությունը ժամանակի ցանկացած պահին (այսինքն՝ ինչպես պահից հետո, այնպես էլ դրանից առաջ).
- ,
- :
Արագացմանը ածաանցյալը ըստ ժամանակի, այսինքն այն ֆիզիկական մեծությունը, որը բնութագրում է արագացման փոփոխման արագությունը, կոչվում է պոկում (հաճախ նշանակվում է )՝
- :
Կորագիծ շարժման վերլուծությունը[խմբագրել | խմբագրել կոդը]

Կորագիծ շարժում կատարող նյութական կետի արագությունը կարելի է ներկայացնել հետևյալ տեսքով․
- ,
որտեղ -ն կամայական պահին արագության մոդուլն է, իսկ
մեծությունը հետագծի կամայական կետում շոշափողով ուղղված միավոր վեկտոր է։ Հաշվի առնելով ինչպես արագության , այնպես էլ միավոր վեկտորի ժամանակային կախվածությունները, կորագիծ շարժում կատարող նյութական կետի արագացումը կգրվի որպես երկու ֆուկցիաների արտադրյալի ածանցյալ, բարդ ֆունկցիայի ածանցյալի բանաձևի կիրառմամբ[5]՝
Այստեղ -ը նյութական կետի հետագծի կամայական կետում շոշափողին ուղղահայաց ուղղությամբ միավոր վեկտորն է, -ը կամայական կետում կորության շառավիղը։ Այսպիսիով, կորագիծ շարժման դեպքում արագացումը ներկայացվում է
տեսքով, որտեղ բաղադրիչը կոչվում է տանգենցիալ կամ շոշափող, իսկ բաղադրիչը՝ նորմալ կամ կենտրոնաձիգ արագացում։
Մասնավոր դեպքեր[խմբագրել | խմբագրել կոդը]
Հավասարաչափ արագացող շարժում[խմբագրել | խմբագրել կոդը]
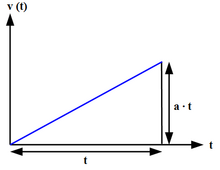
Մասնավոր դեպքում, եթե վեկտորը չի փոխվում ժամանակի ընթացքում, շարժումը կոչվում է հավասարաչափ արագացող։ Հավասարաչափ արագացող շարժման դեպքում -ի և -ի որոշման վերը նշված ընդհանուր բանաձևերը պարզեցվում են, բերվելով հետևյալ տեսքի[6]՝
- ,
- ։
Այստեղ
- -ն նյութական կետի շառավիղ վեկտորն է սկզբնական պահին՝ ,
- -ն նյութական կետի արագությունն է սկզբնական պահին` :
Այսպիսի շարժման տարածված օրինակներից է դիմադրության բացակայության դեպքում մարմնի ազատ անկումը համասեռ գրավիտացիոն դաշտում։ Այդ դեպքում մարմնի վրա ազդող ուժը կլինի
- ,
որտեղ -ն ազատ անկման արագացումն է[7]։

Հավասարաչափ արագացող շարժման մասնավոր դեպքում արագացումը շարժման ամբողջ ժամանակահատվածում հավասար է զրոյի։ Այս դեպքում արագությունը հաստատուն է, իսկ շարժման հետագիծը ուղիղ գիծ է, այդ պատճառով այս շարժումը կոչվում է ուղղագիծ հավասարաչափ շարժում։ Եթե այս դեպքում արագությունը նույնպես հավասար է զրոյի, ապա մարմինը գտնվում է դադարի վիճակում։
Հավասարաչափ արագացող շարժումը նյութական կետի համար միշտ հարթ շարժում է, իսկ պինդ մարմնի համար՝ համընթաց շարժում։ Սակայն հակառակ պնդումը, ընդհանուր դեպքում, ճիշտ չէ։ Հավասարաչափ արագացող շարժումը այլ հաշվարկման իներցիալ համակարգ անցնելիս մնում է հավասարաչափ արագացող։ Հավասարաչափ արագացող շարժման մասնավոր դեպքը, երբ հաստատուն արագացումը և արագությունը ուղղված են մի գծով, սակայն տարբեր ուղղություններով, կոչվում է հավասարաչափ դանդաղող շարժում։ Հավասարաչափ դանդաղող շարժումը միշտ միաչափ է։ Շարժումը կարելի է դիտարկել որպես հավասարաչափ դանդաղող միայն մինչև այն պահը, երբ արագությունը դառնում է զրո։ Բացի այդ, միշտ գոյություն ունեն իներցիալ հաշվարկման համակարգեր, որտեղ շարժումը հավասարաչափ դանդաղող չէ։
Արագացումով շարժման կարևոր մասնավոր դեպք է ուղղագիծ շարժումը, երբ ժամանակի ցանկացած պահի արագացումը համագիծ է արագությանը (օրինակ՝ ուղղահայաց սկզբնական արագությամբ մարմնի անկման դեպքը)։ Ուղղագիծ շարժման դեպքում կարելի է կոորդինատական առանցքներից մեկն ընտրել շարժման ուղղությամբ և փոխարինել շառավիղ-վեկտորը և արագության ու արագացման վեկտորները սկալյարներով։ Հաստատուն արագացման դեպքում վերը բերված բանաձևերից բխում է, որ
- ։
Այստեղ -ն և -ն մարմնի սկզբնական և վերջնական արագություններն են, -ն՝ արագացումը, -ը՝ մարմնի անցած ճանապարհը։
Ստորև ներկայացված են զրոյական սկզբնական արագությամբ հավասարաչափ արագացող ուղղագիծ շարժման գործնականում կարևոր մի շարք բանաձևեր, որոնք կապ են հաստատում մարմնի անցած ճանապարհի, ժամանակի, վերջնական արագության և արագացման միջև՝
- ,
- ,
- ,
- :
Այս մեծություններից ցանկացած երկուսով որոշվում են մյուս երկուսը, համարվում է, որ ժամանակը հաշվարկվում է շարժման սկզբից՝ ։
Շրժանագծային շարժում[խմբագրել | խմբագրել կոդը]

Հավասարաչափ շրջանագծային շարժման դեպքում, երբ նյութական կետը մեծությամբ հաստատուն արագությամբ շարժվում է շրջանագծային հետագծով, նրա արագացումը արդյունք է արագության ուղղության փոփոխության, քանի որ արագության մեծությունը հաստատուն է։ Կորի վրա նյութական կետի դիրքի (այսինքն շառավիղ-վեկտորի) առաջին կարգի ածանցյալը ըստ ժամանակի՝ արագությունը պարզվում է, որ շարժաման ընթացքում անընդհատ ուղղված է կորին տարված շոշափողով, համապատասխանաբար ուղղահայաց լինելով տվյալ կետում շառավղի ուղղությանը։ Քանի որ հավասարաչափ շարժման դեպքում արագությունը տանգենցիալ (շոշափողի) ուղղությամբ հաստատուն է, արագացումը պետք է ուղղված լինի շառավղային ուղղությամբ դեպի շրջանագծի կենտրոնը։ Այդ արագացումը, որը անվանում են կենտրոնաձիգ արագացում, անընդհատ փոխում է արագության ուղղությունը՝ պտտելով այն շրջանագծի երկայնքով։ Տրված արագության դեպքում արագացման մեծությունը ուղիղ համեմատական է արագության քառակուսուն և հակադարձ համեմատական շրջանագծի շառավղին՝
- ։
Արագացման վեկտորը կարելի է արտահայտել բևեռային կոորդինատներով։ Ընդունելով, որ -ը շրջանագծի կենտրոնից մինչև նյութական կետը ուղղված վեկտորն է (շառավղին հավասար մեծությամբ) և հաշվի առնելով, որ արագացումը ուղղված է դեպի կենտրոնը՝
- ։
Ինչպես սովորաբար կատարվում է պտտական շարժումների դեպքում, կարելի է ներմուծել նյութական կետի անկյունային արագությունը՝ արտահայտված նյութական կետի արագությամբ և հեռավորությամբ՝
- ։
Այսպիսով, արագացման համար ստացվում է արտահայտությունը։

Ընդհանուր դեպքում, երբ նյութական կետը շրջանագծային շարժում է կատարում մոդուլով փոփոխական արագությամբ, արագացման վեկտորը կարելի է վերլուծել երկու բաղադրիչների (գումարելիների)՝
- :
տանգենցիալ կամ շոշափող արագացումը ուղղված է հետագծի շոշափողով։ Այն արագացման վեկտորի բաղադրիչն է՝ համագիծ ակնթարթային արագության վեկտորին, և բնութագրում է արագության փոփոխությունը ըստ մոդուլի.
- :
նորմալ կամ կենտրոնաձիգ արագացումը միշտ առաջանում է (հավասար չէ զրոյի) ոչ միայն շրջանագծով շարժման ժամանակ, այլև ցանկացած ոչ զրոյական կորությամբ հետագծով շարժման դեպքում։ Ինչպես նշվել էր, այն արագացման վեկտորի՝ ակնթարթային արագությանը ուղղահայաց բաղադրիչն է, և բնութագրում է արագության փոփոխությունը ըստ ուղղության։
Անկյունային արագացումը ցույց է տալիս անկյունային արագության փոփոխությունը միավոր ժամանակում։ Այն գծային արագացման նման, հաշվարկվում է հետևյալ կերպ՝
Վեկտորի ուղղությունը այստեղ ցույց է տալիս արագության մոդուլի նվազումը կամ աճը։ Եթե անկյունային արագացման և անկյունային արագության վեկտորները համուղղված են, կամ երբ նրանց սկալյար արտադրյալը դրական է, արագության մեծությունը աճում է, և հակառակը։ Հավասարաչափ շրջանագծային շարժման մասնավոր դեպքում անկյունային արագացման և տանգենցիալ արագացման վեկտորները հավասար են զրոյի, իսկ կենտրոնաձիգ արագացումը ըստ մոդուլի հաստատուն է։
Բարդ շարժում[խմբագրել | խմբագրել կոդը]
Ասում են, որ նյութական կետը (մարմինը) կատարում է բարդ շարժում, եթե այն շարժվում է մի հաշվարկման համակարգի նկատմամբ, որն իր հերթին մեկ այլ՝ «լաբորատոր» համակարգի նկատմամբ շարժման մեջ է։ Այդ դեպքում լաբորատոր համակարգում մարմնի բացարձակ արագացումը հավասար կլինի հարաբերական, տեղափոխական և կորիոլիսյան արագացումների գումարին՝
- ։
Վերջին անդամը ներառում է շարժական հաշվարկման համակարգի պտտման անկյունային արագության և այդ համակարգում նյութական կետի արագության վեկտորական արտադրյալը։
Արագացումը պինդ մարմնի կինեմատիկայում[խմբագրել | խմբագրել կոդը]
Բացարձակ պինդ մարմնի երկու և կետերի արագացումների կապը կարելի է ստանալ այդ կետերի արագությունների համար Էյլերի բանաձևից՝
- ,
որտեղ -ն մարմնի անկյունային արագության վեկտորն է, իսկ -ն և կետերը միացնող վեկտորը։ Ածանցելով այս արտահայտությունը ըստ ժամանակի, ստացվում է՝
- ,
որտեղ -ը մարմնի անկյունային արագացման վեկտորն է։ Այս արտահայտությունը անվանում են Ռիվալսի բանաձև[8][9][10]։
Արագացման առաջացումը։ Նյութական կետի դինամիկա[խմբագրել | խմբագրել կոդը]
Նյուտոնի առաջին օրենքը փաստում է հաշվարկման իներցիալ համակարգերի գոյության մասին։ Այդպիսի համակարգերում ուղղագիծ հավասարաչափ շարժումը տեղի ունի այն դեպքում, երբ մարմինը (նյութական կետը) չի ենթարկվում իր շարժման ընթացքում որևէ արտաքին ազդեցության։ Այդ օրենքի հիման վրա ի հայտ է գալիս մեխանիկայում կարևոր դեր ունեցող ուժի գաղափարը՝ ուժը ընկալվում է որպես արտաքին ազդեցություն մարմնի վրա, որը հանում է մարմինը դադարի վիճակից կամ ազդում է շարժման արագության վրա։ Այսպիսով սահմանվում է, որ հաշվարկման իներցիալ համակարգում արագացման ի հայտ գալու պատճառը արտաքին ուժային ազդեցությունն է։
Դասական մեխանիկա[խմբագրել | խմբագրել կոդը]
Նյուտոնի երկրորդ օրենքը՝ կիրառված ոչ ռելյատիվիստիկ շարժման համար (այսինքն լույսի արագությունից շատ փոքր արագությունների դեպքում) փաստում է, որ նյութական կետի արագացումը ուղիղ համեմատական է նրա վրա կիրառված, այդ արագացումը ծնող ուժին, ընդ որում համեմատականության գործակիցը անկախ է ուժային ազդեցության տեսակից և կոչվում է նյութական կետի իներտ զանգված՝
- ։
Եթե հայտնի են նյութական կետի զանգվածը և նրա վրա ազդող ուժը (կախված ժամանակից), ապա Նյուտոնի երկրորդ օրենքից որոշվում է արագացումը՝ ։ Ուժի հաստատուն լինելու դեպքում արագացումը ևս հաստատուն է։ Նյութական կետի արագությունը և կոորդինատները ժամանակի ցանկացած պահին կարելի է որոշել՝ ինտեգրելով արագացումը նյութական կետի կինեմատիկայի բաժնում բերված բանաձևերով սկզբնական պայմանների (սկզբնական արագություն, սկզբնական կոորդինատներ) հաշվառմամբ։
Ռելյատիվիստական մեխանիկա[խմբագրել | խմբագրել կոդը]
Ռելյատիվիստական մեխանիկայում Նյուտոնի երկրորդ օրենքը գրվում է հետևյալ տեսքով․
- ։
Այս դեպքում արագացման որոշման խնդիրը ավելի բարդ է, քան դասական մեխանիկայում։ Մասնավորապես, ռելյատիվիստական մեխանիկայում հաստատուն արագացումով երկարատև շարժումը սկզբունքորեն անհնար է, քանի որ արագությունը կարող է գերազանցել լույսի արագությանը։ Ուժի հաստատուն լինելը չի նշանակում, որ հաստատուն է նաև արագացումը՝ արագության աճին զուգընթաց այն կձգտի զրոյի։ Սակայն եթե կախվածությունը որոշված է, -ի և -ի հաշվարկը կատարվում է նույն ոչ ռելյատիվիստական սահմանի բանաձևերով։
Արագացումը հարաբերականության տեսությունում[խմբագրել | խմբագրել կոդը]
Հարաբերականության տեսությունում քառաչափ տարածություն-ժամանակում փոփոխական արագությամբ մարմնի շարժումը աշխարհագծի երկայնքով բնութագրվում է մի մեծությամբ, որը համարժեք է արագացմանը։ Ի տարբերություն արագացման սովորական եռաչափ վեկտորի, արագացման 4-վեկտորը (որը անվանվում է 4-արագացում) հանդիսանում է կոորդինատների 4-վեկտորի երկրորդ կարգի ածանցյալը ոչ թե ըստ ժամանակի, այլ ըստ տարածաժամանակային ինտերվալի (այն անվանվում է նաև սեփական ժամանակ)՝ աշխարհագծի երկայնքով․
- ։
Աշխարհագծի կամայական կետում արագացման 4-վեկտորը միշտ ուղղահայաց է 4-արագությանը՝
- ։
Սա մասնավորապես նշանակում է, որ արագության 4-վեկտորները մոդուով չեն փոխվում, այլ փոխվում են միայն ուղղությամբ։ Անկախ տարածություն-ժամանակում շարժման ուղղությունից ցանկացած մարմնի 4-արագությունը մոդուլով հավասար է լույսի արագությանը։ Երկրաչափորեն 4-արագացումը համընկնում է աշխարհագծի կորության հետ։
Դասական մեխանիկայում արագացման արժեքը չի փոխվում մի իներցիալ համակարգից մյուսին ացման ժամանակ, այսինքն արագացումը ինվարիանտ է Գալիլեյի ձևափոխությունների նկատմամբ։ Ռելյատիվիստական մեխանիկայում 4-արագացումը 4-վեկտոր է, այսինքն Լորենցի ձևափոխությունների ժամանակ փոխվում է այնպես, ինչպես տարածաժամանակային կոորդինատները։
Արագացման «սովորական» վեկտորը, որը որոշվում է որպես «սովորական» եռաչափ արագության ածանցյալ ըստ կոորդինատային ժամանակի () կիրառելի է ռելյատիվիստական կինեմատիկայի սահմաններում, սակայն ինվարիանտ չէ Լորենցի ձևափոխությունների նկատմամբ։ Հաստատուն ուժի ազդեցության ժամանակ նյութական կետի արագացումը նվազում է արագության աճին զուգընթաց, սակայն 4-արագացումը մնում է հաստատուն (այսպիսի դեպքը անվանում են ռելյատիվիստական հավասարաչափ արագացող շարժում, չնայած «սովորական» արագացումը հաստատուն չէ)։
Արագացման չափումը[խմբագրել | խմբագրել կոդը]
Չափման միավորներ[խմբագրել | խմբագրել կոդը]
Արագացման չափողականությունը համապատասպանում է արագության (LT−1) և ժամանակի հարաբերության չափողականոթյանը՝ LT−2։
- Միավորների միջազգային համակարգում արագացման չափման միավորն է մեկ մետրը քառակուսի վայրկյանում՝ մ·վ−2 կամ մ/վ2։
- Միավորների CGS (ՍԳՎ) համակարգում արագացման չափման միավորը սմ/վ2-ն է։
- Հաճախ նմատակահարմար է չափել խնդրում ի հայտ եկած արագացումը այն համեմատության մեջ դնելով Երկրի մակերևույթի մոտ ազատ անկման արագացման (նշանակվում է ) հետ։ -ի արժեքը 9,80665 մ/վ2 է։ Հաճախ տեխնիկական հաշվարկներում, որոնք չեն պահանջում 2 %-ից մեծ ճշտություն, մոտավորությամբ -ն համարվում է հավասար 10 մ/վ2-ու։
Դասական մեխանիկայում մեխանիկական համակարգի դինամիկան նկարագրվում է ոչ թե դեկարտյան, այլ ընդհանրացված կոորդինատներով (օրինակ՝ համիլտոնյան կամ լագրանժյան ձևակերպումներով), այսպիսով սահմանվում է ընդհանրացված արագացումը որպես ընդհանրացված արագության առաջին կարգի ժամանակային ածանցյալ կամ ընդհանրացված կոորդինատների երկրորդ կարգի ժամանակային ածացյալ։ Օրինակ, որպես ընդհանրացված կոորդինատ կարող է ընտրված լինել անկյունը, այդ դեպքում ընդհանրացված արագացում կլինի անկյունային արագացումը։ Հետևաբար ընդհանրացված արագացման չափողականությունը ընդհանուր դեպքում հավասար չէ LT−2։
| մ/վ2 | ֆուտ/վ2 | սմ/վ2 | ||
|---|---|---|---|---|
| 1 մ/վ2 = | 1 | 3,28084 | 0,101972 | 100 |
| 1 ֆուտ/վ2 = | 0,304800 | 1 | 0,0310810 | 30,4800 |
| 1 = | 9,80665 | 32,1740 | 1 | 980,665 |
| 1 սմ/վ2 = | 0,01 | 0,0328084 | 0,00101972 | 1 |
Չափման տեխնիկական միջոցներ[խմբագրել | խմբագրել կոդը]
Արագացումը չափելու համար նախատեսված սարքը կոչվում է աքսելերոմետր։ Աքսելերոմետրերը չեն գրանցում անմիջականորեն արագացումը, այլ չափում են արագացումով շարժման ժամանակ առաջացող հենարանի հակազդեցության ուժը։ Քանի որ նման դիմադրության ուժերը առաջանում են գրավիտացիոն դաշտում, աքսելերոմետրի միջոցով կարելի է չափել նաև գրավիտացիան։
Արագացումը չափելու համար կիրառվում են նաև աքսելոգրաֆերը, որոնք չափում և գրաֆիկի տեսքով գրանցում են համընթաց և պտտական շարժման արագացումները։
Որոշ դեպքերում արագացման արժեքների աղյուսակ[խմբագրել | խմբագրել կոդը]
Աղյուսակում աճման կարգով ներկայացված են որոշ շարժումների բնութագրական արագացումները[11]։
| Շարժման տեսակը | Արագացումը, մ/վ2 |
|---|---|
| Արեգակնային համակարգի կենտրոնաձիգ արագացումը գալակտիկայում ուղեծրային շարժման ընթացքում | 2,2·10−10 |
| Լուսնի կենտրոնաձիգ արագացումը Երկրի շուրջ ուղեծրային շարժման ընթացքում | 0,0027 |
| Երկրի կենտրոնաձիգ արագացումը Արևի շուրջ ուղեծրային շարժման ընթացքում | 0,0060 |
| Վերելակի շարժումը | 0,9—1,6 |
| Մետրոյի գնացքի շարժումը | 1 |
| «Ժիգուլի» մակնիշի մեքենայի շարժումը | 1,5 |
| Վազորդի վազքը (փոքր հեռավորությունների վրա) | 1,5 |
| Հեծանվորդի շարժումը | 1,7 |
| Չմուշկ քշողի շարժումը | 1,9 |
| Մոտոցիկլետի շարժումը | 3—6 |
| Մեքենայի վթարային արգելակումը | 4—6 |
| Ուսեյն Բոլտի վազքը (առավելագույն արագացումը)[12] | 8 |
| Մրցարշավային մեքենայի շարժումը | 8—9 |
| Պարաշյուտի արգելակումը բացվելիս | 30 (3 ) |
| Տիեզերական թռչող ապարատի արձակումը և արգելակումը | 40—60 (4—6 ) |
| Ռեակտիվ ինքնաթիռի մանևրը | մինչև 100 (մինչև 10 ) |
| Ներքին այրման շարժիչի մխոցի շարժումը | 3·103 |
| Փամփուշտը շարժումը հրացանի փողում | 2,5·105 |
| Միկրոմասնիկների շարժումը արագացուցիչում | (2—50)·1014 |
| Գունավոր հեռուստացույցի խողովակում (20 կՎ, 0,5 մ) կաթոդի և անոդի միջև էլեկտրոնների շարժումը | ≈7·1015 |
| Գունավոր հեռուստացույցի խողովակում (20 կՎ) էլեկտրոնների շարժումը լյումինաֆորին բախվելիս | ≈1022 |
| Ալֆա-մասնիկների շարժումը ատոմի միջուկում | ≈1027 |
Ծանուցում․ այստեղ ազատ անկման արագացումը ընդունվում է հավասար 10 մ/վ2-ու։
Նշումներ[խմբագրել | խմբագրել կոդը]
- ↑ Հոդվածում վեկտորական մեծությունները նշանակված են մուգ տառերով՝ , ինչը համարժեք է ընդունված նշանակմանը։
- ↑ Բոլոր այն դեպքերում, երբ շարժումը տեղի է ունենում ուղիղ գծի երկայնքով, վեկտորական մեծությունները կարող են փոխարինվել սկալյարներով։
- ↑ Անկյունային արգացման համար հաճախ կարող է հանդիպել նաև նշանակումը։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. էջ 43. ISBN 978-0-559-36871-4.
- ↑ Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. էջեր 3. ISBN 978-0-486-24021-3.
- ↑ Lehrman, Robert L. (1998). Physics the Easy Way. Barron's Educational Series. էջեր 27. ISBN 978-0-7641-0236-3.
- ↑ Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). College Physics, Volume 10. Cengage. էջ 32. ISBN 9780495386933.
- ↑ Weisstein, Eric W. «Chain Rule». Wolfram MathWorld. Wolfram Research. Վերցված է 2016 թ․ օգոստոսի 2-ին.
- ↑ Keith Johnson (2001). Physics for you: revised national curriculum edition for GCSE (4th ed.). Nelson Thornes. էջ 135. ISBN 978-0-7487-6236-1.
- ↑ David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding physics. Birkhäuser. էջ 146. ISBN 978-0-387-98756-9.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРо, 1999. — С. 59. — 572 с.
- ↑ Appendice au Mémoire de M. Bresse // Journal de l'École polytechnique. — 1853. — Հ. 20, էջ 109–115։
- ↑ Joulin L. Notice biographique sur M. le commandant Rivals // Mémoires de l'Académie royale des sciences, inscriptions et belles-lettres de Toulouse. — 1891. — Հ. 3, թիվ 9, էջ 535—539։
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп. — М.: Наука, 1988. — С. 61. — 256 с.
- ↑ Ерин Ю. Мировой рекорд в беге на 100 метров мог бы быть лучше // elementy.ru, 23.09.2008։
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Արագացում» հոդվածին։ |
| ||||||
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 1, էջ 680)։ |




































































![{\displaystyle \mathbf {a} =\mathbf {a} _{r'}+\mathbf {a} _{e}+2\left[\mathbf {\omega } ,\mathbf {v} _{r'}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88c8c1f424de1021fc687bc927acaa1268f6bc0e)


![{\displaystyle \mathbf {v} _{\mathrm {B} }=\mathbf {v} _{\mathrm {A} }+\left[\mathbf {\omega } ,\mathbf {AB} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8479ca1680c34238749b18c35424685fc8232656)


![{\displaystyle \mathbf {w} _{\mathrm {B} }=\mathbf {w} _{\mathrm {A} }+\left[\mathbf {\omega } ,\left[\mathbf {\omega } ,\mathbf {AB} \right]\right]+\left[\mathbf {\varepsilon } ,\mathbf {AB} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06594bef4c00777fc8808b15066c69b622ab85ae)
















