Պարադոքս

Պարադոքս (հուն․՝ παράδοξος — անսպասելի, տարօրինակ, ընդունված կարծիքին հակասող), մտահանգում կամ գիտափորձ, որը տալիս է ինքնըստինքյան ճիշտ համարվող, նախադրյալներին հակասող եզրակացություն։ Պարադոքսն իրավիճակ է, որը կարող է լինել իրականում, բայց տրամաբանական բացատրություն չունի։ Առօրյա կյանքում պարադոքսները դրսևորվում են որպես հանրահայտ, համընդհանուր ճանաչում գտած կարծիքի մերժում։ Այս կերպ ըմբռնված պարադոքսը որպես գեղարվեստական հնար կիրառվում է ժողովրդական բանահյուսության մեջ (առակ, ասացվածք, անեկդոտ), գեղարվեստական գրականությունում՝ խոսքի ներգործությունն ուժեղացնելու, միտքը շեշտելու համար։ Հարկ է տարբերել պարադոքսն ապորիայից։ Ապորիան (անտինոմիա), ի տարբերություն պարադոքսի, հորինված, տրամաբանորեն ճիշտ դատողություն կամ իրավիճակ է, որն իրականում գոյություն ունենալ չի կարող։
Տրամաբանական պարադոքսներ (Ոչ մաթեմատիկական)[խմբագրել | խմբագրել կոդը]
Իմպլիկացիայի պարադոքսները[խմբագրել | խմբագրել կոդը]
Իմպլիկացիայի պարադոքսները[1] հիմնված են դասական տրամաբանության[2] պայմանական պնդումների վրա։
Դասական տրամաբանությունում պայմանական պնդումն ունի այս տեսքը՝ «Եթե , ապա »: Այն սխալ է միայն այն դեպքում, երբ -ն ճիշտ է, իսկ -ն՝ սխալ, և այն ճիշտ է մնացած բոլոր դեպքերում։ Այս դեպքում և պնդումների բովանդակությունը հաշվի չի առնվում։ Նույնիսկ եթե նրանք իրար հետ ընդհանրապես կապ չունենան, նրանցով կազմված պնդումը կարող է ճիշտ լինել։
Այսպես են բացատրվում հետևյալ պարադոքսները.
- Եթե -ն ճիշտ է, ապա ամբողջ պնդման ճշմարտացիությունն այլևս կախված չէ -ից։ Այսինքն՝ պնդումը կարող է ապացուցվել ցանկացած պայմանով։ Օրինակ՝ «Եթե 1+1=3, ապա ձյունը սպիտակ է» պնդումը համարվում է ճիշտ։
- Եթե -ն սխալ է, ապա ամբողջ պնդման ճշմարտացիությունը այլևս կախված չէ -ից։ Այսինքն՝ սխալ պայմանով կարելի է ապացուցել ցանկացած պնդում։ Օրինակ՝ «Եթե 1+1=3, ապա ձյունը կանաչ է» պնդումը համարվում է ճիշտ։
- Եթե -ն իրար հակասող պայման է, ապա ամբողջ պնդման ճշմարտացիությունը այլևս կախված չէ -ից։ Այսինքն՝ հակասական պայմանով կարելի է ապացուցել ցանկացած պնդում։ Օրինակ՝ «Եթե 1+1=2 և 1+1 հավասար չէ 2, ապա ձյունը կանաչ է» պնդումը համարվում է ճիշտ։
- Եթե -ն տավտալոգիա[3] է (պնդում, որը ճիշտ է ցանկացած դեպքում), ապա ամբողջ պնդման ճշմարտացիությունը այլևս կախված չէ -ից։ Այսինքն՝ պնդումը ճիշտ է ցանկացած պայմանի դեպքում։ Օրինակ՝ «Եթե ձյունը կանաչ է, ապա 1+1 հավասար է 2 կամ 1+1 հավասար չէ 2» պնդումը համարվում է ճիշտ։
Ագռավների պարադոքսը[խմբագրել | խմբագրել կոդը]

Ագռավների պարադոքսը[4] կամ Հեմպելի պարադոքսն ասում է. «Ինչքան շատ են կարմիր խնձորները, այնքան մեծ է հավանականությունը, որ բոլոր ագռավները սև են»։ Այս պարադոքսը բացատրվում է հետևյալ կերպ.
Ենթադրենք, կա մի թեորեմ, ըստ որի բոլոր ագռավները սև են։ Այս թեորեմը համարժեք է այն թեորեմին, որ «բոլոր ոչ սև առարկաները ագռավ չեն»։ Եթե մի մարդ տեսնի շատ սև ագռավներ, ապա նրա համոզմունքը, որ բոլոր ագռավները սև են, կմեծանա։ Եվ նույն ձևով, եթե մի մարդ տեսնի շատ կարմիր խնձորներ, ապա նրա համոզմունքը, որ բոլոր ոչ սև առարկաները ագռավ չեն, կմեծանա, ինչն ըստ վերը նշված պնդումի պետք է մեծացնի նաև հավանականությունը, որ բոլոր ագռավները սև են։ Սա հակասում է մարդու ինտուիտիվ ընկալմանը։
Անսպասելի մահապատժի պարադոքսը[խմբագրել | խմբագրել կոդը]
Անսպասելի մահապատժի պարադոքսը[5] նկարագրվում է այսպես.
Կիրակի օրը բանտի տնօրենը կանչում է մահապատժի դատապարտված հանցագործին և ասում.
- Ձեր մահապատիժը կիրագործվի հաջորդ շաբաթվա մի օր կեսօրին։
- Մահապատժի օրը Ձեզ համար անակնկալ կլինի, և Դուք կիմանաք այդ մասին միայն այն ժամանակ, երբ դահիճը մտնի Ձեր բանտախուց։
Բանտի տնօրենը շատ արդար մարդ էր և երբեք չէր խաբում։
Բանտարկյալը մտածեց նրա խոսքերի վերաբերյալ և ժպտաց. «Իմ մահապատիժը չեն կարող իրագործել կիրակի օրը, քանի որ ես արդեն շաբաթ երեկոյան համոզված կլինեմ, որ ինձ կիրակի են սպանելու, և դա ինձ համար անակնկալ չի լինի։ Հետևաբար՝ իմ մահապատժի վերջին հնարավոր օրը շաբաթ օրն է, բայց եթե ուրբաթ օրն ինձ չսպանեն, ապա այդ օրն ինձ նույնպես չեն կարող սպանել, քանի որ ես արդեն ուրբաթ երեկոյան համոզված կլինեմ, որ ինձ սպանելու են շաբաթ օրը, և դա ինձ համար անակնկալ չի լինի։ Հետևաբար՝ շաբաթ օրն էլ կարելի է բացառել»։ Այսպես հերթով բացառելով ուրբաթը, հինգշաբթին, չորեքշաբթին, երեքշաբթին և երկուշաբթին՝ բանտարկյալը եզրակացրեց, որ իր բանտի տնօրենը չի կարող իրագործել մահապատիժը՝ հետևելով իր բոլոր խոսքերին։
Հաջորդ շաբաթ դահիճը մտավ բանտախուց չորեքշաբթի կեսօրին։ Սա բանտարկյալի համար լրիվ անսպասելի էր։ Ամեն ինչ, ինչ ասել էր բանտի տնօրենը, կատարվել էր։ Որտե՞ղ էր սխալվել բանտարկյալը։
Այն փաստը, որ բանտարկյալի բոլոր փաստարկները ճիշտ էին, բայց եզրակացությունը՝ սխալ, խոսում է այն մասին, որ բանտարկյալը մինչև վերջ չի ընկալել իրավիճակը։ Որպեսզի չորեքշաբթի օրվա մահապատիժը բանտարկյալի համար անակնկալ չլինի, նա պետք է համոզված լինի, որ իրեն սպանելու են չորեքշաբթի, բայց նա համոզել էր ինքն իրեն, որ մահապատիժը չի կայանալու։

Ընկերության պարադոքս[խմբագրել | խմբագրել կոդը]
Ընկերության պարադոքսը[6] երևույթ է, ըստ որի որպես կանոն, մարդկանց մեծամասնությունն ավելի քիչ ընկեր ունի, քան միջինում իրենց ընկերը։ Երևույթը հայտնաբերել է Նյու Յորքի պետական համալսարանի սոցիոլոգ Սքոթ Ֆելդը 1991 թվականին, երբ ուսումնասիրում էր սոցիալական ցանցերը։
Պարադոքսը ճիշտ է նաև ավելի նեղ իմաստով սոցիալական ցանցերի համար, հատկապես՝ համացանցային սոցիալական ցանցերի (Ֆեյսբուք, Տվիտեր և այլն)։
Չնայած վարկածի ակնհայտ պարադոքսալ լինելուն՝ այն բխում է գրաֆների տեսության և հավանականությունների տեսության հիմնարար սկզբունքներից, որոնք կիրառվում են սոցիալական գրաֆի դեպքում։
Մասնավորապես, պարադոքսը կարելի է բացատրել ընտրանքի տեղաշարժումով, որտեղ մեծաքանակ կապեր ունեցող անձինք ավելի մեծ հավանականություն ունեն հայտնվել ընկերների շարքում։
Ինքնահղման պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Բերրիի պարադոքս[7]. «Ո՞րն է ամենափոքր բնական թիվը, որը հնարավոր չէ բնութագրել 12-ից քիչ քանակի բառերով։»
- Կարրիի պարադոքս[8]. «Եթե այս պնդումը ճիշտ է, ապա ջրահարսերը գոյություն ունեն»
- Կոկորդիլոսի պարադոքս[9]. Կոկորդիլոսը գողանում է երեխային և ասում մորը, որ հետ կտա երեխային, եթե մայրը ճիշտ պատասխանի հարցին՝ «Արդյո՞ք հետ կտա կոկորդիլոսը երեխային»
- Ստախոսի պարադոքս[10]. Կրետացին ասում է. «Բոլոր կրետացիները ստախոս են», կամ Ստախոսն ասում է. «Այս նախադասությունը սուտ է»
- Պետրոնիուսի պարադոքս. «Սահմանափակեք ձեզ ամեն ինչում, նույնիսկ սահմանափակումներում»
- Էվատլի պարադոքս[11]. Պրոտագորը վերցրեց աշակերտության Էվատլին այն պայմանով, որ Էվատլը կվճարի իրեն, երբ հաղթի իր առաջին դատը։ Այնպես եղավ, որ մի օր Պրոտագորը դատի տվեց Էվատլին նրա համար, որ Էվատլը երկար ժամանակ նրան չէր վճարում։ Պե՞տք է Էվատլը վճարի Պրոտագորին, եթե հաղթի այդ դատը։
- Ռոսսելի պարադոքս[12]. Մորուք սափրողը սափրում է միայն այն մարդկանց, ովքեր իրենք իրենց չեն սափրում։ Սափրու՞մ է արդյոք մորուք սափրողն ինքն իրեն։
- Ամենակարողության պարադոքս[13]. Կարո՞ղ է արդյոք ամենակարողը ստեղծել այնպիսի մի քար, որը ինքը չի կարող բարձրացնել։
Սահմանումների պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Թեսևսի նավը[14]. Եթե Թեսևսի նավի ամեն մասնիկ փոխվել է առնվազն մեկ անգամ, կարելի՞ է նավը նույն հին նավը համարել։
- Կույտի պարադոքս[15]. Ո՞ր պահին կույտը այլևս կույտ չի համարվի, եթե կույտից մի-մի հատ հատիկ վերցնենք։
- Ճաղատի պարադոքս. Եթե մարդու գլխից մազերը հատ-հատ են թափվում, ո՞ր պահից մարդը ճաղատ կհամարվի։
- Անհետաքրքիր/Հետաքրքիր թվերի պարադոքս. Ամենափոքր անհետաքրքիր թիվը հետաքրքիր է հենց միայն այն փաստի համար, որ նա ամենափոքր անհետաքրքիր թիվն է։
Մաթեմատիկական պարադոքսներ[խմբագրել | խմբագրել կոդը]
Ալաբամայի պարադոքսը[խմբագրել | խմբագրել կոդը]
Ալաբամայի պարադոքսը[16] առաջացավ 1880 թվականին, երբ մարդահամարից հետո որոշում էին ԱՄՆ Կոնգրեսում Ալաբամա նահանգի ներկայացուցիչների քանակը Համիլտոնի կլորացման մեթոդի փոփոխությունից հետո։ Պարզ դարձավ, որ երբ պատգամավորների ընդհանուր քանակը 299 էր, Ալաբաման ստանում էր 8 ներկայացուցիչ Կոնգրեսում, իսկ երբ պատգամավորների ընդհանուր քանակը 300 էր՝ Ալաբաման ստանում էր 7 ներկայացուցիչ։
Պատճառը նրանում է, որ Համիլտոնի կլորացման մեթոդից հետո ավելի մեծ նահանգներին հասնում է ավելի մեծ աճ, իսկ փոքրներին՝ փոքր։ Դրա հետևանքով փոքր նահանգները կարող են ձայն կորցնել Կոնգրեսում, ինչն էլ տեղի ունեցավ Ալաբամայի օրինակում։
Ոչ տրանզիտիվ զառերի պարադոքսը[խմբագրել | խմբագրել կոդը]

Ոչ տրանզիտիվ զառերի պարադոքսը[17] կայանում է հենց ոչ տրանզիտիվ զառերի գոյության մեջ։ Գոյություն ունեն 3 տարբեր զառեր։ Նշանակենք դրանք , և : Հավանականությունը, որ զառը գցելուց հետո ավելի մեծ թիվ կստացվի, քան զառը գցելիս 50%-ից շատ է։ Հավանականությունը, որ զառը գցելիս ավելի մեծ թիվ կստացվի, քան զառը գցելիս նույնպես 50%-ից շատ է։ Բայց եթե ասենք, որ հավանականությունը, որ զառը գցելուց հետո հետո ավելի մեծ թիվ կստացվի, քան զառը գցելիս 50%-ից շատ է՝ կսխալվենք։
Օրինակ՝
զառի կողմերի վրա գրված են 2, 2, 4, 4, 9, 9
զառի կողմերի վրա գրված են 1, 1, 6, 6, 8, 8
զառի կողմերի վրա գրված են 3, 3, 5, 5, 7, 7
Պենիի խաղը[խմբագրել | խմբագրել կոդը]
Պենիի խաղը խաղում են 2 հոգի՝ օրինակ՝ -ն և -ն։ Սկզբից -ն է 2 թվից բաղկացած (օրինակ՝ 0 և 1) 3 թվի երկարությամբ հաջորդականություն գրում և ցույց տալիս խաղացողին, ապա նույնը անում է -ն։ Հետո, խաղացողները մի հերթականություն են ստեղծում պատահական սկզբունքով, որտեղ 1 կամ 0 ընկնելու հավանականությունները հավասար են։ Օրինակ՝ մետաղադրամ են գցում, նախապես պայմանավորվելով, որ օրինակ «ղուշը» 1 է, իսկ «գիրը»՝ 0 : Հաջորդականություն գրելուց հետո, ում 3 թվերը առաջինը հայտնվեցին հաջորդականության մեջ ճիշտ հերթականությամբ՝ հաղթում է։
Օրինակ՝ խաղացողը ընտրել է հաջորդականություն 001, իսկ խաղացողը՝ 100: Մետաղադրամ գցելուց հետո ստացան 10100։ 100-ը կա հաջորդականության մեջ, այսինքն՝ խաղացողը հաղթում է։
Պարադոքսն այն է, որ խաղացողի ընտրած ցանկացած կոմբինացիայից հետո խաղացողը կարող է ընտրել այնպիսի կոմբինացիա, որի հաղթելու հավանականությունը ավելի շատ է քան 50%-ը։ Եթե խաղացողը -ից հետո ճիշտ կոմբինացիա ընտրի, նրա հաղթանակի հավանականությունը ամենավատ դեպքում 2/3 է։
Այս աղյուսակը ցույց է տալիս, թե որն է -ի եռյակի ամենալավ տարբերակը (այն տարբերակը, որի հաղթելու հավանականությունը ամենամեծն է) -ի ընտրած ամեն եռյակի համար։ -ի ընտրած տարբերակները գրված են վերևի տողում, իսկ -ինները՝ ձախ սյունակում։ Նրանց հատման կետը -ի ընտրած կոմբինացիայի հաղթելու հավանականությունն է։
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | |
| 000 | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| 001 | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| 010 | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| 011 | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| 100 | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| 101 | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| 110 | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| 111 | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 |
Մոնթի Հոլլի պարադոքսը[խմբագրել | խմբագրել կոդը]
Մոնթի Հոլլի պարադոքսը[18] հավանականությունների տեսության հայտնի խնդիրներից մեկն է, որի լուծումը, առաջին հայացքից, հակասում է ողջամտությանը։

Խնդիրը ձևակերպվում է որպես խաղի նկարագրություն, ամերիկյան հեռուստատեսային «Let's Make a Deal» շոուի հիման վրա։ Այս խնդրի առավել տարածված ձևակերպումը, որը հրապարակվել է 1990թ. Parade Magazine ամսագրում հետևյալն է.
«Պատկերացրեք, որ դուք մասնակից եք դարձել մի խաղի, որում դուք պետք է ընտրեք երեք դռներից մեկը։ Դռներից մեկի ետևում գտնվում է ավտոմեքենա, իսկ մյուսների ետևում`այծեր։ Դուք ընտրում եք դռներից մեկը, ենթադրենք դա կլինի թիվ դուռը, ապա` հաղորդավարը, որը գիտի, թե որտեղ է մեքենան և որտեղ այծերը, բացում է մնացած դռներից մեկը, օրինակ՝ թիվ դուռը, որի ետևում այծ է։ Այնուհետև նա հարցնում է ձեզ, թե չեք ցանկանում արդյոք փոխել Ձեր ընտրությունը և ընտրել թիվ դուռը։ Արդյո՞ք ձեր ավտոմեքենա շահելու հնարավորությունները կմեծանան, եթե դուք ընդունեք հաղորդավարի առաջարկը և փոխեք ձեր ընտրությունը։»
Հրապարակումից հետո միանգամից պարզ դարձավ, որ խնդիրը ճշգրիտ ձևակերպված չէ`ոչ բոլոր պայմաններն են նշված։ Օրինակ՝ ծրագրի հաղորդավարը կարող է հավատարիմ մնալ «սատանայական Monty» ռազմավարությանը. առաջարկել փոխել ընտրությունը միայն այն դեպքում, երբ խաղացողը առաջին անգամից ընտրել է մեքենան։ Ակնհայտ է, որ նախնական ընտրության փոփոխությունը կհանգեցնի պարտության։
Առավել հայտնի է լրացուցիչ պայմաններով խնդիրը, երբ մասնակցին նախապես հայտնի են հետևյալ կանոնները։
- Մեքենան հավասար հավանականություններով տեղադրված է ցանկացած երեք դռներից մեկի ետևում։
- Հաղորդավարը ցանկացած դեպքում պարտավոր է բացել դուռը, որի ետևում այծ է (բայց ոչ խաղացողի ընտրած դուռը) և առաջարկել խաղացողին փոխել ընտրությունը։
- Եթե հաղորդավարը ունի որևէ դուռ ընտրելու հնարավորություն, ապա նրա դուռ ընտրելու հավանականությունները հավասար են։
Բացատրություններից մեկը հետևյալն է. Եթե դուք փոխում եք ընտրությունը հաղորդավարի գործողություններից հետո, ապա դուք հաղթում եք, եթե ի սկզբանե ընտրված էր սխալ դուռը։ Այսինքն, հավանականությունը 2/3 է, քանի որ ի սկզբանե կարելի է սխալ դուռ ընտրել 3 հնարավոր եղանակներից երկուսով։
Սովորաբար այս խնդիրը տրամաբանում են հետևյալ կերպ. հաղորդավարը միշտ ի վերջո հեռացնում է սխալ դռներից մեկը, և այս դեպքում երկու դռներից ավտոմեքենա ընտրելու հավանականությունը դառնում է 1/2, անկախ նախնական ընտրությունից։ Բայց այս եղանակը այնքան էլ ճիշտ չէ։
Այս եզրակացությունը հակասում է մարդկանց մեծամասնության ինտուիտիվ ընկալմանը, այսինքն Monty Hall-ի պարադոքսը պարադոքս է առօրյա իմաստով։
Բերկսոնի պարադոքսը[խմբագրել | խմբագրել կոդը]
Բերկսոնի պարադոքսը[19] (Բերկսոնի սխալը) ձևակերպվում է այսպես. «Երկու իրար հետ կապ չունեցող իրադարձություն կարող են դառնալ իրարից պայմանական կախված, եթե տեղի ունենա մեկ այլ իրադարձություն։
Ցույց տանք օրինակի վրա.
Վերցնենք նամականիշները։ Նրանց կարելի է բնութագրել հետևյալ 2 չափանիշներով՝ «գեղեցկություն» և «հազվադեպություն»
Ենթադրենք, ունենք 1000 նամականիշ, որոնցից 300-ը գեղեցիկ են, իսկ 100-ը հազվադեպ հանդիպող, ընդ որում 30-ը՝ և՛ գեղեցիկ, և՛ հազվադեպ։ Ակնհայտ է, որ բոլոր նամականիշներից 10%-ն է հազվադեպ և գեղեցիկ նամականիշներից նույնպես 10%-ն է հազվադեպ հանդիպող։ Այսինքն՝ նամականիշի գեղեցկությունը ոչինչ չի ասում նամականիշի հազվադիպության մասին։
Բայց եթե վերցնենք այդ նամականիշների միջի բոլոր գեղեցիկ և հազվադեպ նամականիշները (ընդհանուր՝ 370), ապա կստացվի, որ այս ընտրույթի մեջ հազվադեպ նամականիշները կազմում են 27%, բայց եթե վերցնենք միայն գեղեցիկ նամականիշները, նրանց մեջ հազվադեպ նամականիշները կկազմեն 10%։ Թվում է, թե այս ընտրույթի մեջ, գեղեցիկ նամականիշները հազվադեպ նամականիշների հետ հակադարձ համեմատական են (եթե նամականիշը գեղեցիկ է, ապա նրա հազվադիպության հավանականությունը ավելի փոքր է), ինչը այդպես չէ։ Այստեղ է պարադոքսի պարադոքսությունը։
Տարեդարձի պարադոքսը[խմբագրել | խմբագրել կոդը]

Տարեդարձի պարադոքսը[20] ասում է. «Եթե խմբում կա 23 կամ ավելի մարդ, ապա հավանականությունը, որ առնվազն երկու հոգի ծնվել են նույն օրը (օր և ամիս) 50%-ից ավելի է։» 60-ից ավել մարդկանց համար այս հավանականությունը 99%-ից ավելի է։ Այս պարադոքսը մաթեմատիկորեն ապացուցված է, և պարադոքս է համարվում միայն այն պատճառով, որ հակասում է մարդկանց ինտուիտիվ ընկալմանը, քանի որ մարդը մտածում է, որ մարդկանց տարեդարձերի համընկման հավանականությունը 0.27% է, բազմապատկած 23-ով՝ կստացվի ընդամենը : Այս դատողությունը սխալ է, քանի որ հնարավոր զույգերի քանակը անհամեմատ գերազանցում է խմբում մարդկանց քանակը :
Բերտրանի արկղերի պարադոքսը[խմբագրել | խմբագրել կոդը]
Բերտրանի արկղերի պարադոքսը[21] գրվել է 1889 թվականին Ժոզեֆ Բերտրանի կողմից։ Այն շատ է օգտագործվում հավանականությունների տեսությունը բացատրելու համար։
Ենթանդրենք ունենք 3 արկղ.
-ի մեջ 2 հատ ոսկե մետաղադրամ է
-ի մեջ 2 հատ արծաթե մետաղադրամ է
-ի մեջ 1 ոսկե մետաղադրամ է և 1 արծաթե մետաղադրամ
Դուք պատահական սկզբունքով ընտրում եք մեկ արկղ և նրա միջից 1 մետաղադրամ։ Մետաղադրամը ոսկուց է լինում։ Ինչքա՞ն է հավանականությունը, որ այդ արկղի մյուս մետաղադրամը նույնպես ոսկուց է (այսինքն պատահական արկղը համար 1 արկղն է)։ Մարդկանց մեծամասնությունը կպատասխանի 1/2, բայց ճիշտ պատասխանը 2/3 է, քանի որ համար արկղի մեջ կա 2 ոսկե մետաղադրամ, իսկ ընդհանուր՝ 3:
2 ծրարների պարադոքսը[խմբագրել | խմբագրել կոդը]
2 ծրարների պարադոքսը[22] նույնպես իրենից խաղ է ներկայացնում

Բոբին տալիս են 2 ծրար, որոնցից մեկի մեջ 2 անգամ ավելի շատ գումար կա, քան մյուսի մեջ։ Թե ինչքան գումար կա ծրարներում՝ Բոբը չգիտի։ Նաև չգիտի, թե որի մեջ ավելի շատ գումար կա։ Բոբը վերցնում է մի ծրարը, և առանց ծրարի պարունակությունը նայելու, Բոբին առաջարկում են փոխել ծրարը։ Հիմա պե՞տք է արդյոք Բոբը փոխի ծրարը, թե՞ ոչ։ Բոբը հաշվում է այսպես.
Ես տեսնում եմ իմ ծրարի մեջ քանակի գումար։ Եթե փոխեմ ծրարը կստանամ կամ քանակի գումար, կամ քանակի գումար։ Միջինով՝ , այսինքն իմ գումարը կմեծանա և արժի փոխել։ Փոխելուց հետո, Բոբին անում են նույն առաջարկը՝ առանց նայելու ծրարի պարունակությունը փոխել ծրարը, և Բոբը անելով նույն դատողությունները, հանգում է այն եզրակացության, որ արժի նորից փոխել ծրարը։ Եվ այսպես կարելի է անվերջ շարունակել։ Որտե՞ղ է Բոբի սխալը։
Սխալն այն է, որ հաշվվել է ծրարների միջին թվաբանականը, ինչը կարելի է անել միայն այն դեպքում, երբ 2 ծրարներն էլ Բոբի մոտ լինեին։
Կորած քառակուսու հանելուկ[խմբագրել | խմբագրել կոդը]
Կորած քառակուսու հանելուկը տեսողական խաբկանքի վրա հիմնված երկրաչափական խնդիր է։ Միևնույն պատկերներով ստացվում են 13×5 չափսերի ուղղանկյուն եռանկյունիներ, սակայն երկրորդում ունենում ենք 1×1 դատարկ քառակուսի։ Հանելուկն ուսանողներինին օգնում է երկրաչափական պատկերների մասին պատկերացում կազմելու։
Այլ մաթեմատիկական պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Գալիլեյի պարադոքս[23]։ Չնայած ոչ բոլոր բնական թվերն են ինչ-որ թվերի լրիվ քառակուսի, բնական թվերը լրիվ քառակուսիներից շատ չեն։
- Հիլբերտի «Գրանդ հոթել» պարադոքս[24]։ Եթե անվերջ քանակությամբ սենյակներով հյուրանոցը լրիվ զբաղված է, միևնույն է նրա մեջ կարելի է տեղավորել էլի մարդկանց, նույնիսկ՝ անվերջ քանակությամբ մարդկանց։
- Տարսկիի շրջանի քառակուսացումը[25]։ Հնարավո՞ր է արդյոք բաժանել շրջանը մասերի և դրանք ուրիշ ձևով դասավորելով, ստանալ նույն մակերեսով քառակուսի։

- Բանախ-Տարսկիի պարադոքս[26]։ Կարելի է վերցնել գունդը, բաժանել այն 5 մասի, իրենց դասավորել ուրիշ ձևով և ստանալ 2 գունդ՝ նույն շառավղով ինչ սկզբնական գունդը։
- Ջրափնյա գծի պարադոքս[27]։ Ցամաքի ջրափնյա գիծը չունի հստակ որոշված երկարություն և սահմաններ։
Ընտրության հետ կապված պարադոքսներ[խմբագրել | խմբագրել կոդը]
Աբիլինի պարադոքս[խմբագրել | խմբագրել կոդը]
Աբիլինի պարադոքսը[28] կայանում է նրանում, որ մի խումբ մարդիկ կարող են ընդունել որոշում, որը հակասում է տվյալ խմբի յուրաքանչյուր անդամի առանձին ընտրությանը, միայն այն պատճառով, որ ամեն մեկը կարծում է, թե իր նպատակները հակասում են խմբի նպատակներին, ուստի չի առարկում։
Օրինակ՝
Բուրիդանի ավանակը[խմբագրել | խմբագրել կոդը]

Բուրիդանի ավանակի պարադոքսի[29] հարցն է, թե ի՞նչ ընտրություն է անելու ավանակը, որը գտնվում է երկու հավասարապես գայթակղիչ խոտի դեզերի միջև։
Վարկած կա, որ ավանակը, չկարողանալով ընտրություն անել, չի ուտի և սովից կսատկի։ Ըստ խնդրի տրամաբանության կարելի է եզրակացնել, որ ավանակը սովից չի սատկի, թեև չենք կարող վստահաբար ասել, թե որ դեզը կընտրի։ Ուտելիքից հրաժարվելը նույնպես կարելի է ընտրություն հաշվել։
Կա նաև վարկած, որ կարելի է միացնել 2 դեզերը։
Հսկողության պարադոքս[խմբագրել | խմբագրել կոդը]
Ըստ հսկողության պարադոքսի[30], մարդ չի կարող լինել ամբողջովին ազատ հսկողությունից, քանի որ դրա համար նա պետք է հսկի ինքն իրեն։ Կարդալ ավելին (անգլ.)
Քիմիական պարադոքսներ[խմբագրել | խմբագրել կոդը]
Լեվինտալի պարադոքս[խմբագրել | խմբագրել կոդը]
Լեվինտալի պարադոքսը[31] հայտնի պարադոքս է, որը ձևակերպվել է 1968թ. Սայրուս Լեվինտալի կողմից. «Ժամանակահատվածը, որի ընթացքում պոլիպեպտիդը հասնում է իր ոլորված վիճակին, ավելի շատ է, քան եթե պոլիպեպտիդը փորձեր բոլոր հնարավոր դասավորվածությունները»։
Ֆիզիկական պարադոքսներ[խմբագրել | խմբագրել կոդը]
Բելլի պարադոքս[խմբագրել | խմբագրել կոդը]

Բելլի պարադոքսը[32] հարաբերականությունների հատուկ տեսության ռելյատիվիստիկ պարադոքսներից մեկն է՝ կապված տարածաժամանակային հարաբերականության տեսության մեջ «բացարձակ պինդ մարմին» հասկացության որոշման անհնարինության հետ։ Բելլի պարադոքսը ծագում է մտային փորձի քննարկման ժամանակ, որը պարունակում է իր մեջ նույն ուղղությամբ արագացված երկու տիեզերանավեր և մինչև վերջ ձգված լար, որը միացնում է նրանց (մի տիեզերանավը խիստ որոշակիորեն շարժվում է մյուսի առջևից, այսինքն՝ արագացումն ուղղված է լարի երկայնքով)։ Եթե տիեզերանավերը սկսեն համաչափ կերպով արագացվել, ապա նավերին ուղեկցող հաշվարկի համակարգում նրանց միջև հեռավորությունը կսկսի աճել, և լարը կկտրվի։ Մյուս կողմից, այն հաշվանքի համակարգում, որտեղ տիեզերանավերը սկզբում դադարի վիճակում էին, նրանց միջև հեռավորությունը չի փոխվի, հետևաբար լարը չի կտրվի։ Ո՞ր տեսակետն է ճիշտ։
Էյնշտեյն-Պոդոլսկի-Ռոզենի պարադոքս[խմբագրել | խմբագրել կոդը]
Էյնշտեյնի-Պոդոլսկու-Ռոզենի պարադոքսը (ԷՊՌ պարադոքս)[33] մտային փորձի օգնությամբ քվանտային մեխանիկայի ոչ կատարյալ լինելը ցույց տալու փորձ է, որի էությունը միկրոօբյեկտների պարամետրերի մտովի չափումն է՝ առանց նրանց վրա որևէ ազդեցության։
ԷՊՌ փորձը, հեղինակների տեսանկյունից, հնարավորություն է տալիս միաժամանակ ճշգրտորեն չափել մասնիկի կոորդինատն ու իմպուլսը։ Միևնույն ժամանակ քվանտային մեխանիկայում ապացուցվում է, որ այդպիսի չափումներն անհնարին են։ Դրանց հիման վրա Էյնշտեյնը, Պոդոլսկին և Ռոզենը եզրակացություն կատարեցին քվանտային տեսության ոչ կատարյալ լինելու մասին։ Իրականում փորձը չի հակասում քվանտային մեխանիկային և հեշտությամբ լուծվում է նրա օգնությամբ։ Թվացյալ հակասությունն առաջանում է այն պատճառով, որ չափումներ հասկացությունն ունի մի քանի տարբեր իմաստներ դասական և քվանտային տեսություններում։
Սանդուղքի պարադոքս[խմբագրել | խմբագրել կոդը]

Սանդուղքի և ավտոտնակի պարադոքսը[34] մտային փորձ է հարաբերականությունների տեսության վերաբերյալ։ Պարադոքսի ամենահեշտ տարբերակում ասվում է.
Ունենք ավտոտնակ, որը 2 կողմից դռներ ունի, և սանդուղք, որի երկարությունը ավտոտնակի լայնությունից շատ ավելի երկար է, և սանդուղքը ոչ մի ձև տեղ չի անում ավտոտնակում։ Մենք հասցնում ենք սանդուղքը մեծ հորիզանական արագության, նրան անցկացնելով բաց դռներով ավտոտնակի միջով։ Մեծ արագության շնորհիվ սանդուղքը ենթարկվեց երկարության կրճատման և զգալիորեն կարճացավ։ Դրա արդյունքում սանդուղքը որոշ ժամանակ ամբողջությամբ տեղավորվում է ավտոտնակում։ Սա ցույց տալու համար կարելի է փակել ավտոտնակի դռները։
Մինչև հիմա ոչ մի պարադոքս չենք տեսնում։ Պարադոքսը կառաջանա, երբ մենք դիտարկենք իրավիճակը սանդուղքի տեսանկյունից։ Հարաբերականությունների տեսության համաձայն, նույն իրավիճակը կարող ենք դիտարկել սանդուղքի տեսանկյունից։ Այս դեպքում սանդուղքը միշտ կանգնած է մնում, իսկ ավտոտնակը շարժվում է մեծ արագությամբ, այսինքն՝ կարելի է դիտարկել նույն երկարության կրճատման էֆեկտը սանդուղքի վրա, և կստացվի, որ ավտոտնակի լայնությունն է փոքրանում, և մենք չենք կարող փակել նրա դռները, երբ սանդուղքը ներսում է։
Շրյոդինգերի կատուն[խմբագրել | խմբագրել կոդը]
Շրյոդինգերի կատուն[35] մտային փորձ է, որպես լուսաբանություն քվանտային մեխանիկայի կոպենհագենյան մեկնաբանության խնդրին, երբ այն կիրառվում է առօրյա օբյեկտների նկատմամբ։
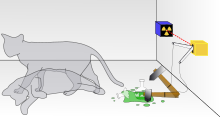
Փակ տուփում տեղադրված է կատու, թունավոր գազով լի սրվակ և ռադիոակտիվ միջուկի վրա հիմնված մեխանիզմ։ Փորձի պարամետրերն ընտրված են այնպես, որ ռադիոակտիվ միջուկը մեկ ժամվա ընթացքում 1/2 հավանականությամբ կարող է տրոհվել։ Եթե միջուկը տրոհվի, դա կհանգեցնի նրան, որ մեխանիզմը կաշխատի, սրվակը կջարդվի և կատուն կմեռնի։ Ըստ քվանտային մեխանիկայի, քանի դեռ միջուկի վրա փորձ չի կատարվել, նրա վիճակը նկարագրվում է քվանտային վերադրման սկզբունքով՝ տրոհված և չտրոհված միջուկների վիճակում, հետևաբար, եթե կատուն նստած է տուփում, նա և՛ ողջ է, և՛ մահացած միաժամանակ։ Եթե դուք բացեք այդ տուփը, փորձարարը կարող է տեսնել միայն ինչ-որ մի հատուկ վիճակ՝ «միջուկը փլուզված է և կատուն զոհված» կամ «միջուկը տրոհվում է, իսկ կատուն ողջ է»։
Հարցն այն է, երբ համակարգը դադարում է գոյություն ունենալ սուպերպոզիցիոն վիճակում ու ընտրում է մեկը։ Քանի որ պարզ է, որ կատուն պետք է լինի ողջ կամ մահացած (չկա միջանկյալ վիճակ կյանքի և մահվան միջև), դա նշանակում է, որ սա ճշմարիտ է ատոմային միջուկի համար։ Դա, անկասկած, լինելու է կա՛մ տրոհված կա՛մ չտրոհված։
Երկվորյակների պարադոքս[խմբագրել | խմբագրել կոդը]
Երկվորյակների պարադոքսը նույնպես հարաբերականությունների հատուկ տեսության մտային փորձերից է։ Երկրի վրա գտնվող երկվորյակներից մեկը մեկնում է տիեզերական ճամփորդության և երբ վերադառնում է, պարզվում է, որ Երկրի վրա մնացած եղբայրն իրենից ավելի տարիքով է։ Այս արդյունքը շփոթեցնող է թվում, քանի որ երկվորյակներից յուրաքանչյուրը մյուսին տեսնում է շարժման մեջ, հետևաբար՝ համաձայն ժամանակի դանդաղման և հարաբերականությունների տեսության ոչ ճիշտ կիրառության՝ երկվորյակներից յուրաքանչյուրը պետք է գտներ, որ մյուսն ավելի դանդաղ է հասակ առնում։ Սակայն այս խնդիրը կարելի է լուծել հարաբերականությունների հատուկ տեսության ստանդարտ շրջանակներում․ ճամփորդող երկվորյակի հետագիծը ընդգրկված է երկու տարբեր իներցիալ համակարգերում, որոնցից մեկը հեռավոր ճամփորդությունն է ներկայացնում, մյուսը՝ վերադարձը։ Հետևաբար երկվորյակների տարածաժամանակների գծերն իրար հանդեպ սիմետրիկ չեն։ Ուրեմն երկվորյակների պարադոքսը պարադոքս չէ տրամաբանական հակասականության իմաստով։
Սպանված պապիկի պարադոքս[խմբագրել | խմբագրել կոդը]
Սպանված պապիկի պարադոքսը[36] ժամանակի միջով տեղափոխվելու մասին պարադոքսներից է, որը գրել է Ռենե Բերժավելը 1943թ.
Պարադոքսը բնութագրվում է այսպես. Դուք ունեք ժամանակի մեքենա և տեղափոխվում եք անցյալ, որտեղ տեսնում եք Ձեր պապիկին և սպանում նրան, մինչև նա կհանդիպի Ձեր տատիկին։ Հետևաբար չի ծնվի Ձեր ծնողներից մեկը և Դուք, հետևաբար Դուք չեք կարողանա հետ գնալ անցյալ և սպանել Ձեր պապիկին, հետևաբար նա կհանդիպի Ձեր տատիկին և կծնվեք Դուք, հետևաբար կկարողանաք հետ գնալ անցյալ և սպանել նրան։

Հիդրոդինամիկական պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Դ՛Ալամբերի պարադոքս[37]. Պնդում հիդրոդինամիկայի մեջ իդեալական հեղուկի մասին, ըստ որի՝ պինդ հեղուկի անընդհատ, անսահման, ոչ մածուցիկ հոսանքով ստացիոնար հոսման ժամանակ մարմնի դիմացի և հետևի մասերի պարամետրերի հավասարության դեպքում, դիմադրության ուժը հավասար է զրոյի։
- Արքիմեդի պարադոքս[38]. Հսկա նավը կարող է լողալ մի քանի լիտր ջրի մեջ։
- Թեյի տերևների պարադոքս[39]. Թեյը գդալով շրջանաձև խառնելիս, մենք տեսնում ենք, որ թեյի տերևները հավաքվում են բաժակի հատակի կենտրոնում, իսկ ըստ մարդու ինտուիտիվ մտածելակերպի՝ կենտրոնախույս ուժի ազդեցությամբ տերևները պետք է հավաքվեին բաժակի ծայրերին։ Այս պարադոքսը լուծել է Ալբերտ Այնշտայնը։
Տերմոդինամիկական պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Տիեզերքի Ջերմային մահը(Heat death of the universe). Ըստ Ռուդոլֆ Կլաուզիսի, տիեզերքը պետք է գա տերմոդինամիկական հավասարակշռության կամ «ջերմային մահի»։ Եվ այս դեպքում բոլոր տեսակի էներգիաները պետք է վերածվեն ջերմային էներգիայի։
- Մպեմբայի պարադոքս[40]. Տաք ջուրը (որոշ պայմաններում) կարող է ավելի արագ սառել, քան ավելի սառը ջուրը, չնայած որ այդ սառելու ընթացքում նա պետք է անցնի նաև սառը ջրի ջերմաստիճանով։

- Մաքսվելի հրեշ[41]. Մաքսվելի հրեշը թույլ է տալիս տաքացնել անոթի աջ կողմը և սառեցնել ձախը՝ առանց համակարգին ավելորդ էներգիա տալու։ Ձախ և աջ մասերից կազմված անոթի սկզբնական վիճակի դեպքում համակարգի էնտրոպիան ավելին է, քան վերջնական վիճակի դեպքում, որը հակասում է փակ համակարգերում էնտրոպիայի չնվազելու տերմոդինամիկական սկզբունքին։
- Գիբսի պարադոքս[42]. Եթե բացակայում է անընդհատությունը էնտրոպիայի համար՝ տարբեր գազերի խառնումից միանման գազերի խառնմանը անցնելու ժամանակ, էնտրոպիայի խառնման նախնական արժեքը դառնում է զրո։
Այլ ֆիզիկական պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Մասնիկ-ալիքային երկվություն[43]. Տեսություն, ըստ որի մատերիան օժտված է ոչ միայն զանգված ունեցող մասնիկի հատկություններով, այլև՝ ալիքի, որն էներգիա է տեղափոխում։
- Բրաեսի պարադոքս[44]. Ցանցում, որի մեջ մասնիկները իրենք են ընտրում իրենց ուղին, լրացուցիչ մասնիկների ավելացումը կարող է փոքրացնել ցանցի ընդհանուր արդյունավետությունը։
- Ֆերմիի պարադոքս[45]. Արտերկրային քաղաքակրթության գործունեության երևացող հետքերը բացակայում են, չնայած որ նրանք պետք է տարածվեին ամբողջ տիեզերքով իրենց գոյության միլիարդավոր տարիների ընթացքում։
- Ֆոտոմետրիկ պարադոքս[46] (Օլբերսի պարադոքս, Շեզո-Օլբերսի պարադոքս). Ստացիոնար տիեզերքում, որում հավասարապես լցված են աստղերը (ինչպես որ ընդունված էր), երկնքի պայծառությունը (ինչպես նաև գիշերային երկնքի) պետք է մոտավորապես հավասար լինի արևի պայծառությանը։
- Հիդրոստատիկական պարադոքս[47]. Ոչ գլանաձև անոթում լցված հեղուկի կշիռը հավասար չէ անոթի հատակին ազդող հեղուկի ճնշման ուժին։
- Էրենֆեստի պարադոքս[48]. Մտային փորձ, ըստ որի ի սկզբանե անշարժ պինդ մարմնի շրջանագիծը պետք է պտույտից հետո պարադոքսալ կերպով կրճատի իր շառավիղը, որպեսզի պահպանի երկարությունը։
Փիլիսոփայական պարադոքսներ[խմբագրել | խմբագրել կոդը]
- Հավի և ձվի խնդիր[49]. Ի՞նչն է եղել ավելի շուտ՝ հավը, թե՞ ձուն։ Մի կողմից հավի առաջացման համար անհրաժեշտ է ձու, մյուս կողմից՝ ձվի առաջացման համար անհրաժեշտ է հավ։
- Չարի խնդիր[50]. Թվում է, թե չարի և ամենակարողի գոյությունը անհամատեղելի են։
- Նյուկոմի պարադոքս[51]. Մտավոր փորձ՝ խաղ 2 մասնակիցների միջև՝ գուշակի (ով անսխալ գուշակում է ապագան) և հենց խաղացողի։
Զենոնի ապորիաներ[խմբագրել | խմբագրել կոդը]

Աքիլեսը և կրիան[խմբագրել | խմբագրել կոդը]
«Աքիլեսը և կրիան» ապորիան[52] ասում է, որ Աքիլեսը ինչքան էլ կրիայից արագ լինի, չի կարող հասնել նրան, եթե կրիան նրանից առաջ է գտնվում և Աքիլեսի նման առաջ է գնում.
Դիխոտոմիա[խմբագրել | խմբագրել կոդը]
Դիխոտոմիան[53] էլ Զենոնի ապորիաներից է և ցույց է տալիս շարժման մաթեմատիկական մոդելի հակասականությունը.
Այսինքն՝ ըստ դիխոտոմիայի մենք չենք կարող շարժվել մեր տեղից։
Թռչող նետը[խմբագրել | խմբագրել կոդը]
Զենոնի «Թռչող նետը» ապորիան[54] ուղղված է անընդհատ մեծության՝ որպես անսահման քանակի մասնիկների (ժամանակի պահ, տարածության կետ) ընկալման դեմ.
| Թռչող նետը ժամանակի ամեն պահի իրեն հավասար դիրքում է, այսինքն՝ կանգնած է։ Հետևաբար՝ կարելի է եզրակացնել, որ թռչող նետը միշտ կանգնած է |
Տնտեսական[խմբագրել | խմբագրել կոդը]
Ալլեի պարադոքս[խմբագրել | խմբագրել կոդը]
Ալլեի պարադոքսը[55] բիզնեսի մեջ ռիսկերի և որոշումների կայացման վառ օրինակներից է։
Ալլեն կատարեց մի փորձ, որը նկարագրվում է ներքևում և ստացավ պարադոքսալ արդյունք։
Անհատներին առաջարկվում է կատարել ընտրություն 2 զույգ ռիսկային տարբերակների մեջ։
Առաջին դեպքում տարբերակում կա 100% հնարավորություն ստանալու 1մլն ֆրանկ, իսկ տարբերակում կա 89% հնարավորություն ստանալ 1մլն ֆրանկ, 10% հնարավորություն ստանալու 2.5մլն ֆրանկ և 1% հնարավորություն ոչինչ չստանալու
Իսկ երկրորդ դեպքում տարբերակում կա 90% հնարավորություն ոչինչ չստանալու և 10% հնարավորություն ստանալու 5մլն ֆրանկ, իսկ տարբերակում կա 89% հնարավորություն ոչինչ չստանալու և 11% հնարավորություն ստանալու 1մլն ֆրանկ։
Փորձը ցույց տվեց, որ մարդկանց մեծամասնությունն ընտրում է տարբերակը առաջին դեպքում և տարբերակը երկրորդ դեպքում, ինչը ըստ գոյություն ունեցող տեսակետի պարադոքսալ է։

Խնայողության պարադոքս[խմբագրել | խմբագրել կոդը]
Խնայողության պարադոքսը[56] սահմանվում է այս կերպ. «Ինչքան շատ ենք մենք խնայում սև օրվա համար, այնքան ավելի շուտ է այն մոտենում»։ Եթե տնտեսական անկման ժամանակ բոլորը սկսեն խնայել, ապա ընդհանուր պահանջարկը կընկնի, ինչի պատճառով աշխատավարձերը կնվազեն, ինչի հետևանքով՝ խնայողությունները կփոքրանան։ Այսինքն՝ կարելի է պնդել, որ երբ բոլորը խնայում են, դա հանգեցնում է ընդհանուր պահանջարկի փոքրացմանը և տնտեսական աճի դանդաղեցմանը։
Գրեշեմի պարադոքս[խմբագրել | խմբագրել կոդը]
Գրեշեմի (Գրեշեմ-Կոպերնիկոսի) պարադոքսը[57] սահմանվում է այսպես. «Վատ փողերը դուրս են մղում լավ փողերին»
Ձևակերպվում է նաև այս եղանակներով.
«Փողերը, որոնք գերագնահատված են պետության կողմից, օգտագործումից դուրս են մղում այն փողերը, որոնք արհեստականորեն թերագնահատված են վերջինիս կողմից»
«Էժան փողերը դուրս են մղում թանկ փողերին»
«Փողերը, որոնցով կարելի է հարկեր չվճարել, դուրս են մղում այն փողերը, որոնցով հարկ վճարելը պարտադիր է»
«Վատագույն փողերը օգտագործումից դուրս են մղում ավելի լավ փողերը, եթե փոխարժեքը օրենքով է սահմանված»
Գիֆենյան ապրանքներ[խմբագրել | խմբագրել կոդը]
Գիֆենի ապրանքները[58] ապրանքներն են, որոնք չեն ենթարկվում «պահանջարկի օրենքին», այսինքն՝ գների բարձրացմանը զուգընթաց դրանց սպառման ծավալն աճում է։
Գիֆենի ապրանք կարող է լինել ոչ միայն հացը, այլև բնակչության աղքատ խավերի համար լայն սպառման ապրանքներ։ Օրինակ՝ ի՞նչ տեղի ունեցավ ՀՀ–ում, երբ միանգամից բարձրացան հացի և կարտոֆիլի գները։ Պատկերացրեք աղքատ ընտանիքների վիճակը (իսկ այդպիսիք մեզ մոտ կազմում էին ընտանիքների առնվազն 3/4-ը), որոնք օգտագործում էին որոշ քանակությամբ հաց, կարտոֆիլ, միս և այլ ապրանքներ։ Նրանք սկսեցին ավելի շատ հաց և կարտոֆիլ գնել, իսկ հետո՝ միայն հաց։ Ինչու՞: Որովհետև նրանց եկամուտներն այլևս թույլ չէին տալիս միս և այլ ապրանքներ գնել, և ամբողջ եկամուտը ուղղվում էր հաց և կարտոֆիլ գնելուն (իսկ ոմանք միայն հաց գնելուն)։ Հետևաբար մեծացավ այս ապրանքների սպառումը և գնորդների կախվածությունը դրանցից։
Ապրանքների սպառումը հետաքրքիր օրինաչափությամբ կախված է նաև եկամտի էֆեկտից (income effect) և փոխարինման էֆեկտից (substitution effect)։ Եթե ապրանքը ցածրորակ է (inferior good), ապա նրա նկատմամբ պահանջարկը սպառողների հարստացմանը զուգընթաց ընկնում է։ Այսպիսի ապրանքների գնի բարձրացումը կարող է հանգեցնել նաև պահանջարկի բարձրացմանը, իսկ գնի իջեցումը՝ պահանջարկի անկման։ Օրինակ, հարուստ երկրների համար ցածրորակ ապրանքներ են հեծանիվը, ապխտած երշիկը, մարգարինը և այլն։
Լեոնտևի պարադոքս[խմբագրել | խմբագրել կոդը]
Ըստ Լեոնտևի պարադոքսի[59], որոշ երկրներ արտահանում են աշխատածախս ապրանքներ, իսկ ներմուծում՝ կապիտալածախս ապրանքներ, ինչը հակասում է Հեկշեր-Օլինի թեորեմին։ Կարդալ ավելին (անգլ.)
Տես նաև[խմբագրել | խմբագրել կոդը]
- Կարագով կատվի պարադոքս
- Անհնարին պատկերներ
- Տրամաբանական սխալներ
- Տեսողական պատրանք
- Գլուխկոտրուկներ
- 0,(9) = 1
- Գիտական անբացատրելի պարադոքսներ Արխիվացված 2017-02-03 Wayback Machine
- 11 Brain-Twisting Paradoxes
- Paradox Of The Day
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ «парадоксы импликации - это... Что такое парадоксы импликации?». Словари и энциклопедии на Академике (ռուսերեն). Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ Shapiro, Stewart (2013 թ․ հունվարի 1). Zalta, Edward N. (ed.). Classical Logic (Winter 2013 ed.). Metaphysics Research Lab, Stanford University.
- ↑ «ТАВТОЛОГИЯ - это... Что такое ТАВТОЛОГИЯ?». Словари и энциклопедии на Академике (ռուսերեն). Վերցված է 2017 թ․ ապրիլի 12-ին.
- ↑ «Raven Paradox - Hempel's Logic Example and Inductive Reasoning». Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ W., Weisstein, Eric. «Unexpected Hanging Paradox». mathworld.wolfram.com (անգլերեն). Վերցված է 2017 թ․ ապրիլի 16-ին.
{{cite web}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) - ↑ Metro.co.uk, Ellen Scott for (2016 թ․ մայիսի 21). «JSYK, all of your friends have more friends than you». Metro. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «The Berry Paradox». www.cs.auckland.ac.nz. Արխիվացված է օրիգինալից 2016 թ․ հոկտեմբերի 5-ին. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Beall, Jc (2013 թ․ հունվարի 1). Zalta, Edward N. (ed.). Curry's Paradox (Spring 2013 ed.). Metaphysics Research Lab, Stanford University.
- ↑ «Crocodile Dilemma». perdurabo10.tripod.com. Վերցված է 2017 թ․ ապրիլի 12-ին.
- ↑ «Liar Paradox | Internet Encyclopedia of Philosophy». www.iep.utm.edu (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Protagoras's Paradox». Ancient History Encyclopedia. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Irvine, Andrew David; Deutsch, Harry (2016 թ․ հունվարի 1). Zalta, Edward N. (ed.). Russell's Paradox (Winter 2016 ed.). Metaphysics Research Lab, Stanford University.
- ↑ Hoffman, Joshua; Rosenkrantz, Gary (2012 թ․ հունվարի 1). Zalta, Edward N. (ed.). Omnipotence (Spring 2012 ed.). Metaphysics Research Lab, Stanford University.
- ↑ «Ship of Theseus paradox | Paradox of the day .com». Paradox of the day .com (ամերիկյան անգլերեն). 2014 թ․ օգոստոսի 8. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Hyde, Dominic (2014 թ․ հունվարի 1). Zalta, Edward N. (ed.). Sorites Paradox (Winter 2014 ed.). Metaphysics Research Lab, Stanford University.
- ↑ «Apportionment Paradoxes». www.ctl.ua.edu. Արխիվացված է օրիգինալից 2017 թ․ մայիսի 9-ին. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Balanced Non-Transitive Dice» (PDF).
- ↑ «Understanding the Monty Hall Problem – BetterExplained». betterexplained.com (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ «Berkson's paradox». mathemathinking.blogspot.com. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Understanding the Birthday Paradox – BetterExplained». betterexplained.com (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ «Bertrand's box paradox - Oxford Reference» (անգլերեն). doi:10.1093/oi/authority.20110803095501915.
{{cite journal}}: Cite journal requires|journal=(օգնություն) - ↑ «The Two Envelope Problem». web.mit.edu. Արխիվացված է օրիգինալից 2017 թ․ մայիսի 21-ին. Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ «Galileo's Paradox: An Infinite Series of Square Numbers». Decoded Science (ամերիկյան անգլերեն). 2011 թ․ սեպտեմբերի 5. Արխիվացված է օրիգինալից 2016 թ․ օգոստոսի 16-ին. Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ «Hilbert's Hotel : nrich.maths.org». nrich.maths.org. Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ «The Circle-Squaring Problem Decomposed» (PDF).
- ↑ «THE BANACH-TARSKI PARADOX» (PDF). Արխիվացված է օրիգինալից (PDF) 2017 թ․ հունիսի 23-ին.
- ↑ «coastline paradox | IB Maths Resources from British International School Phuket». ibmathsresources.com (անգլերեն). Վերցված է 2017 թ․ ապրիլի 13-ին.
- ↑ «The Abilene Paradox: The Management of Agreement» (PDF). Արխիվացված է օրիգինալից (PDF) 2020 թ․ հոկտեմբերի 19-ին.
- ↑ «Paradox Resolved: Buridan's Ass». steve-patterson.com (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 14-ին.
- ↑ «Misplaced Confidences: Privacy and the Control Paradox» (PDF).
- ↑ Karplus, Martin (1997 թ․ հունիսի 1). «The Levinthal paradox: yesterday and today». Folding and Design. 2, Supplement 1: S69–S75. doi:10.1016/S1359-0278(97)00067-9.
- ↑ «Speakable and Unspeakable in Quantum Mechanics - Cambridge University Press». www.cambridge.org (անգլերեն). Վերցված է 2017 թ․ ապրիլի 14-ին.
- ↑ Fine, Arthur (2016 թ․ հունվարի 1). Zalta, Edward N. (ed.). The Einstein-Podolsky-Rosen Argument in Quantum Theory (Fall 2016 ed.). Metaphysics Research Lab, Stanford University.
- ↑ «The Ladder Paradox of Special Relativity». www.einsteins-theory-of-relativity-4engineers.com. Վերցված է 2017 թ․ ապրիլի 14-ին.
- ↑ «Schrödinger's Cat». www.informationphilosopher.com. Վերցված է 2017 թ․ ապրիլի 14-ին.
- ↑ «The Grandfather Paradox». A Time Travel Website (ամերիկյան անգլերեն). Արխիվացված է օրիգինալից 2014 թ․ հուլիսի 7-ին. Վերցված է 2017 թ․ ապրիլի 14-ին.
- ↑ «Resolution of D'Alembert's Paradox». The Secret of Flight (ամերիկյան անգլերեն). 2012 թ․ փետրվարի 29. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Gutenberg, Project. «Archimedes paradox | Project Gutenberg Self-Publishing - eBooks | Read eBooks online». www.gutenberg.cc. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Einstein's Tea Leaves and Pressure Systems in the Atmosphere» (PDF). Արխիվացված է օրիգինալից (PDF) 2016 թ․ մարտի 4-ին.
- ↑ «Can hot water freeze faster than cold water?». math.ucr.edu. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Maxwell's demon | physics». Encyclopedia Britannica (անգլերեն). Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «THE GIBBS PARADOX» (PDF).
- ↑ «Wave-Particle Duality». www.informationphilosopher.com. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Braess' paradox» (PDF).
- ↑ «Fermi Paradox | SETI Institute». www.seti.org. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Olbers' Paradox». math.ucr.edu. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Jr., Thomas B. Greenslade,. «Hydrostatic Paradox». physics.kenyon.edu. Արխիվացված է օրիգինալից 2017 թ․ մայիսի 31-ին. Վերցված է 2017 թ․ ապրիլի 16-ին.
{{cite web}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) CS1 սպաս․ հավելյալ կետադրություն (link) - ↑ «Resolution of the Ehrenfest Paradox» (PDF). Արխիվացված է օրիգինալից (PDF) 2015 թ․ սեպտեմբերի 22-ին.
- ↑ «Which Came First, the Chicken or the Egg?». Time. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Tooley, Michael (2015 թ․ հունվարի 1). Zalta, Edward N. (ed.). The Problem of Evil (Fall 2015 ed.). Metaphysics Research Lab, Stanford University.
- ↑ Bellos, Alex (2016 թ․ նոյեմբերի 28). «Newcomb's problem divides philosophers. Which side are you on?». The Guardian (բրիտանական անգլերեն). ISSN 0261-3077. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Zeno's Paradox of the Tortoise and Achilles». platonicrealms.com. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «What is Zeno's Dichotomy Paradox? - Colm Kelleher». TED-Ed. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Zeno's Paradox of the Arrow». faculty.washington.edu. Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ «Allais Paradox» (PDF).
- ↑ Staff, Investopedia (2010 թ․ հունիսի 25). «Paradox Of Thrift». Investopedia (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ Staff, Investopedia (2010 թ․ փետրվարի 9). «Gresham's Law». Investopedia (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 16-ին.
- ↑ CFA, Elvis Picardo, (2010 թ․ մայիսի 27). «Giffen Good». Investopedia (ամերիկյան անգլերեն). Վերցված է 2017 թ․ ապրիլի 16-ին.
{{cite news}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link) CS1 սպաս․ հավելյալ կետադրություն (link) - ↑ «Լեոնտևի պարադոքսը» (PDF).
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Պարադոքս» հոդվածին։ |
| ||||||
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի՝ 2017 թվականի մայիսի 3-ի օրվա հոդված: |

















