Ուժեղ փոխազդեցություն

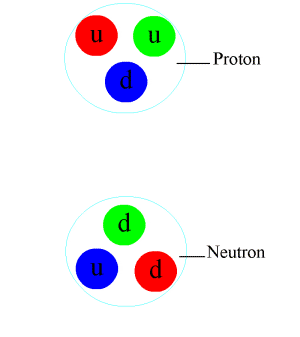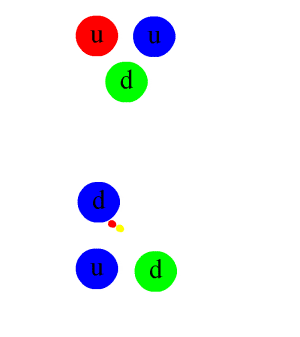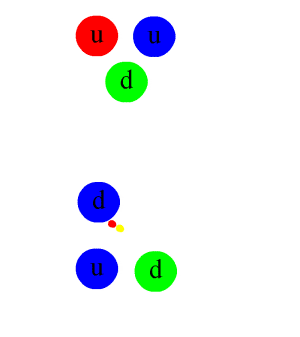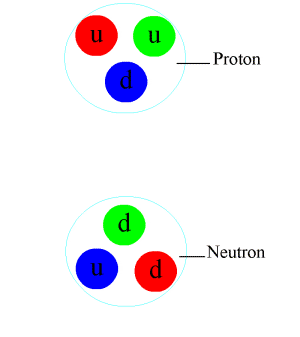
Ուժեղ միջուկային փոխազդեցություն (գունային փոխազդեցություն, միջուկային փոխազդեցություն) չորս հիմնարար փոխազդեցություններից մեկը։ Ուժեղ փոխազդեցությանը մասնակցում են քվարկները և գլյուոնները, և նրանցից կազմված մասնիկները, որոնք կոչվում են հադրոններ (բարիոններ և մեզոններ)։ Նրանք գործում են ատոմի միջուկի սահմանների և ավելի փոքր հեռավորություններում և պատասխանատու են միջուկում քվարկների կապի և նուկլոնների միջև ձգողության համար (բարիոնների տարատեսակներն են պրոտոնները և նեյտրոնները)
Պիոն-նուկլոնային փոխազդեցություն[խմբագրել | խմբագրել կոդը]

Ուժեղ փոխազդեցություն գաղափարի ներմուծման անհրաժեշտություն ծագեց 1930-ական թվականներին, երբ պարզ դարձավ, որ ո՛չ ձգողական, և ո՛չ էլ էլեկտրամագնիսական փոխազդեցության երևույթները չեն կարող պատասխանել այն հարցին, թե ի՞նչն է միավորում նուկլոնները միջուկում։ 1935 թվականին ճապոնացի ֆիզիկոս Հիդեկի Յուկավան կառուցեց նուկլոնների փոխազդեցության առաջին քանակական հաստատունները, որոնք այժմ հայտնի են պի-մեզոններ կամ պիոններ։ Հետագայում՝ 1947 թվականին, պիոնները հայտնաբերվեցին փորձարարական ճանապարհով։
Այս պիոն-նուկլոնային տեսության մեջ երկու նուկլոնների ձգումը կամ վանումը նկարագրվում էր նուկլոնի կողմից պիոնի արտանետմամբ և հաջորդ նուկլոնի կողմից նրա կլանմամբ (համանմանորեն էլեկտրամագնիսական փոխազդեցությանը, որը նկարագրվում է որպես վիրտուալ ֆոտոնի փոխանակում)։ Այդ տեսությունը հաջողությամբ նկարագրում է նուկլոն-նուկլոնային փոխազդեցությունների, ինչպես նաև պիոնների և նուկլոնների, և նրանց կապված վիճակների մի ողջ շարք։ Արտանետման էֆեկտիվությունը նկարագրող քանակական գործակիցը բավականին մեծ էր (համեմատած համանման էլեկտրամագնիսական փոխազդեցության գործակցի հետ), որն էլ բացատրում է ուժեղ փոխազդեցության «ուժը»։
Նուկլոնների փոխազդեցություն ատոմի միջուկում[խմբագրել | խմբագրել կոդը]

մ կարգի հեռավորությունների վրա, միջուկը կազմող նուկլոնների ուժեղ փոխազդեցության մեծությունը այնքան մեծ է, որ թույլատրում է պրակտիկորեն հաշվի չառնել նրանց էլեկտրամագնիսական փոխազդեցությունը (վանողությունը)։ Ընդհանրապես, նուկլոնների փոխազդեցությունը միջուկում «տարրական» չէ, ավելի շուտ այն մասնիկների միջև գործող ուժեղ փոխազդեցության առկայության անմիջական հետևանք է, որպես օրինակ, նուկլոնը կազմող քվարկների փոխազդեցության Վան-Դեր-Վալսյան ուժերը, որոնք բացատրվում են էլեկտրամագնիսական փոխազդեցության գոյությամբ։ Երկու նուկլոնների փոխազդեցության պոտենցիալ ֆունկցիան, լավագույն մոտավորությամբ նկարագրվում է հետևյալ արտահայտությամբ՝
որտեղ ն ուժեղ փոխազդեցության գործակիցն է, սովորաբար այն համարվում է, որ հավասար է -ի՝ հիմնարար փոխազդեցությունների «հաստատունների համակարգում», որտեղ, օրինակ, էլեկտրամագնիսական փոխազդեցության հաստատունը հավասար է Նուրբ կառուցվածքի հաստատունին (այսպիսի պոտենցիալ ֆունկցիան կոչվում է Յուկավայի պոտենցիալ)։ Այս ֆունկցիայի մոդուլը արագորեն նվազում է, և հեռավորությունների վրա աննշան փոքր է։ Ընդհանրապես միջուկի շառավիղը կարելի որոշել մոտավոր բանաձևով, որտեղ ն միջուկի նուկլոնների ընդհանուր թիվն է։ Այստեղից կարելի է, մասնավորապես, շատ մոտավոր գտնել մեզոնի զանգվածը, որպես ուժեղ փոխազդեցության կրողի (առաջին անգամ դա իրականացվել է ճապոնացի ֆիզիկոս Հիդեկի Յուկավայի կողմից)։ Դրա համար, սակայն, պետք է մի քանի առաջարկ անել, որոնք բազմակողմանի ուսումնասիրման ժամանակ կարող են անհիմն թվալ։ Ենթադրենք, որ նուկլոնի կողմից արձակվել է մեզոնը, և կատարելով, մեկ «պտույտ» պոտենցիալային փոսի եզրին (առաջարկներից առաջինը), կլանվում է մյուսի կողմից։ Մաքսիմալ, հետևաբար և, ամենահավանական ալիքի երկարությունը այդ ժամանակ հավասար է : Մեզոնի իմպուլսը՝
որտեղ ն Պլանկի հաստատունն է։ Եթե մենք հիմա ( մեզոնի զանգվածի որոշման համար) ենթադրենք, որ այն ճշգրտորեն հավասար է միջուկում, շարժման ժամանակ ունեցած զանգվածին, ապա դա թերագնահատում կլինի։ Նույն ձևով, եթե ենթադրենք, որ միջուկում մեզոնի արագությունը մոտավորապես հավասար է լույսի արագությանը, ապա այն նույնպես ճշգրիտ չի լինի։ Կոպիտ մոտավորության դեպքում կարող ենք ենթադրել, որ, եթե մենք մեզոնի իմպուլսը հավասարեցնենք ի, ( ն լույսի արագությունն է վակուումում), երկու «անճշտությունները» իրար կչեզոքացնեն։ Այդ ժամանակ՝
Այժմ առավել ֆիզիկորեն արդարացի կլինի, որ այստեղ տեղադրենք , քանի որ խոսքը երկու նուկլոնների մասին էր։ Այդ ժամանակ՝
- կգ։
Այս մեծությունը համարյա հավասար է ի, որտեղ ն էլեկտրոնի զանգվածն է։ Իրականում, միջուկային փոխազդեցության կրողը հանդիսացող մեզոնի զանգվածը, կազմում է մոտավորապես կգ, որը առավել ճշգրիտ հաշվարկների արդյունք է, որոնց արդյունքում օգտագործվում են քվանտային մեխանիկայի համակարգի «առավել կատարելագործված» տարրեր (չնայած, հավանաբար, կարելի էր «վերցնել» զանգվածով էկզոտիկ մեզոն)։ Նուկլոնների միջին արագությունը, միջուկային նյությում, գնահատելու համար հնարավոր է Ֆերմի-գազի մոդելի վրա[1]։ Փուլային տարածության ծավալը, որն համապատասխանում է միավոր ծավալում մասնիկների «ֆիզիկական» տարածությանը, որոնց իմպուլսները է, որտեղ ն որոնվող սահմանային իմպուլսն է, հավասար է : Բաժանելով այն ի, կստանանք «վանդակների» քանակը, որոնցում կտեղավորվեն երկուական պրոտոն և նեյտրոն։ Ենթադրելով, որ պրոտոնների թիվը հավասար է նեյտրոնների թվին, կստանանք
որտեղ ն միջուկի ծավալն է, բանաձևից նրա շառավղի համար կստանանք , որտեղ մ է։ Արդյունքում ֆերմի-իմպուլսի համար կստանանք՝
- կգմվ ՄէՎ/վ։
Հադրոնների ուժեղ փոխազդեցության ֆենոմենոլոգիա[խմբագրել | խմբագրել կոդը]
1950-ական թվականներին հայտնագործվեց տարրական մասնիկների ահռելի քանակություն, որոնցից մեծ մասը օժտված էին կյանքի շատ կարճ տևողությամբ։ Այս բոլոր մասնիկները ուժեղ փոխազդող էին՝ միջուկի էֆեկտիվ կտրվածքում նրանց տեղաբաշխումը մեկի մյուսի նկատմամբ, նուկլոնների և պիոնների փոխազդեցության կտրվածքի կարգի էին, և էականորեն գերազանցում էին էլեկտրոնների հետ նրանց փոխազդեցության կտրվածքը։ Այս հադրոնների մեջ կային ինչպես մեզոններ, այնպես էլ բարիոններ։ Նրանք օժտված էին տարբեր սպիններով և էլեկտրական լիցքերով, զանգվածի իրենց արժեքներով և նախընտրելի տրոհման ուղիներով, նկատելի էր դառնում պարբերականությունը, սակյան որտեղից էր այն առաջանում՝ անհասկանալի էր։ Պիոն-նուկլոնային ցրմանը համանմանորեն կառուցվել է հադրոնների ուժեղ փոխազդեցությունների մոդելը, որտեղ փոխազդեցության յուրաքանչյուր տիպին, յուրաքանչյուր ցրմանը համապատասխանում է իր որոշակի փոխազդեցության հաստատունը։ Բացի դրանից, դիտարկվսծ կախումներից որոշները չհաջողվեց բացատրել, և նրանք, «խաղի կանոններին» համապատաասխան, ուղղակի որպես պոստուլատ համարվեցին, որոնց ենթարկվում են հադրոնները (Ցվեյգի օրենքի, իզոսպինի և G-զույգության պահպանումը և այլն)։ Չնայած նրան, որ ընդհանուր առմամբ, այս նկարագիրը գործում էր, այն, անխոս, բավարար չէր տեսական տեսակետից՝ առավելագույնս շատ էր պոստուլատների թիվը, ազատ պարամետրերի մեծ քանակությունը ներմուծվում էր բոլորովին կամայականորեն ու առանց որևէ սխեմայի։ 1960-ականների կեսերին հայտնագործվել է հադրոնների հատկությունների Մարի Գել-Մանի մատրիցաները՝ SU(3) համաչափությունը, և հասկանալի դառավ, որ ազատության սկզբունքային աստիճանները հադրոնների «կազմավորման» դեպքում, այնքան էլ շատ չէ։ Այդ ազատության աստիճանները ստացան քվարկներ անվանումը։ Մի քանի տարի անց կատարված փորձերը ցուցադրեցին, որ քվարկները՝ ոչ միայն հադրոնի ազատության աստիճանի բացարձակ, այլև իրական մասնիկներ են, որոնցից բաղկացած են հադրոնները, որոնք էլ նրա իմպուլսի, էլեկտրական լիցքի և սպինի կրիչներն են և այլն։ Միակ պրոբլեմը կայանում էր նրանում, թե ինչպես նկարագրեն այն փաստը, որ քվարկները չեն կարող դուրս պրծնել հադրոններից՝ կամայական ռեակցիաների ժամանակ։ Այնուամենայնիվ, քվարկների փոխազդեցության դինամիկ նկարագրության տեսական բացակայության դեպքում անգամ, արդեն այն փաստը, որ հադրոնները՝ բաղկացուցիչ մասնիկներ են, թույլատրեց բացատրել հադրոնների շատ էմպիրիկ հատկություններ։
Քվանտային քրոմոդինամիկայի ուժեղ փոխազդեցություններ[խմբագրել | խմբագրել կոդը]
1970-ական թվականներին կառուցվել է քվարկների ուժեղ փոխազդեցության միկրոսկոպիկ տեսությունը, որը ստացել է քվանտային քրոմոդինամիկա անվանումը (ՔՔԴ)։ Պոստուլատացվում է, որ յուրաքանչյուր քվարկ օժտված է նոր ներքին քվանտային թվով, որը պայմանականորեն անվանվում է գույնով։ Առավել ճշգրտորեն, ազատության նախկին մակարդակներին ի հավելումն, քվարկին վերագրվում է վիճակի որոշակի վեկտոր՝ համակարգված եռաչափ գունային տարածության մեջ։ Տրամաչափային մոտեցման դեպքում դրվում է մեր աշխարհի դիտվող հատկությունների ինվարիանտության պահանջը ունիտար պտույտների համեմատության հետ՝ քվարկների գունային տարածության մեջ, այսինքն SU(3) խմբի տարրերի հետ։ Այսպիսով, ՔՔԴ-ն հանդիսանում է Յանգ-Միլսի տեսությունը։ Համատեղ ծագող տրամաչափային դաշտը հենց նկարագրում է քվարկների փոխազդեցությունը։ Այս դաշտը հնարավոր է դառնում քվանտացնել, և նրա քվանտները կոչվում են գլյուոններ։
Քանի որ, գունային տարածության մեջ, գլյուոնների յուրաքանչյուր տիպ տալիս է իր որոշակի տեսակը, անկախ գլյուոնային դաշտերի քանակը հավասար է SU(3) խմբի չափայնությանը, այսինքն ութի։ Սակայն բոլոր գլյուոնները փոխազդում են բոլոր քվարկների հետ միևնույն ուժով։ Քվանտային էլեկտրադինամիկային համանման, որտեղ փոխազդեցության «հզորությունը» բնութագրվում է նուրբ թաղանթների հաստատուն՝ α-ով,, ուժեղ փոխազդեցության «հզորությունը» բնութագրվում է ուժեղ փոխազդեցության հաստատունով։ Ընդգծենք, որ գլյուոնները գույներով են փոխազդում։ Այն բանի համար, որ SU(3) խումբը Աբելյան խումբ չէ, գլյունները նույնպես օժտված են գույնով, և նշանակում է, որ կարող են իրար հետ փոխազդել, և ըստ տեսության առաջանում են Ֆեյնմանի դիագրամի եռանկյուն և քառանկյուն գագաթներ։ Սրանում էլ կայանում է ՔՔԴ-ի սկզբունքային տարբերությունը Քվանտային էլեկտրադինամիկայից, որտեղ ֆոտոնը լիցքավորված չլինելու պատճառով, չէր փոխազդում ինքն իր հետ։ Ընդգծենք նաև, որ քվարկներից և հակաքվարկներից կարելի է ստանալ կոմբինացիաներ, որոնք ունեն «զրոյական» գույն, այսինքն անգույն են։ Երկարալիքային տիրույթում այսպիսի վիճակներով գլյուոնները չեն փոխազդում։ ՔՔԴ-ի հաջորդ կարևորագույն հատկությունը 'լիցքի հակաէկրանավորումն է։ SU(3)-ի խմբային հատկությունները բերում են նրան, որ ուժեղ փոխազդեցության կապի հաստատունը փոքրանում է քվարկների միջև եղած հեռավորության փոքրացման հետ, և մեծանում է քվարկների իրարից հեռանալուն զուգընթաց։ Այս կախումներից առաջինը հանգեցնում է ասիմպտոտիկ ազատությանը՝ իրար մոտ հեռավորությամբ թռչող քվարկները կարելի է առաջին մոտավորությամբ համարել չփոխազդող։ Մեդալի հակառակ կողմը՝ քվարկների կոնֆայմենթն է կամ գերումը։ Դա նշանակում է, որ քվարկները չեն կարող կոնֆայմենթի որոշակի շառավղի արժեքից առավել իրարից հեռանալ (1 ֆմ-ի կարգի)։ Սակայն երկու անգույն վիճակները կարող են իրարից հեռանալ կամայական հեռավորությամբ, քանի որ նրանց գլյուոնային դաշտը իրենց չի պահում։ Արդյունքում ստացվում է, որ իրական աշխարհում դիտվում են ոչ թե ազատ քվարկներ, այլ նրանց անգույն կոմբինացիաները, որոնք էլ նույնականացվում են հադրոնների հետ։ Հեռացված լինելով կոնֆայմենթի շառավիղը գերազանցող հեռավորությամբ, հադրոնները ամեն դեպքում փոխազդում են, սակայն արդեն ոչ թե գլյուոնների փոխանակման հաշվին, այլ այլ հադրոնների փոխանակման պատճառով։ Մասնավորապես, ցածր էներգիաների դեպքում առավել ուժեղ են ստացվում պի մեզոններով փոխանակումները՝ ուժեղ փոխազդեցություններ (տես վերևը)։ Այսպիսի փոխազդեցությունը (որով, իմիջիայլոց, և պահվում է միջուկում նուկլոնները), նույնպես ավանդականորեն անվանվում է ուժեղ։ Սակայն, պետք է հասկանալ, որ այս «մնացորդային» ուժեղ փոխազդեցությունը, համանման է Վան-դեր-Վալսյան փոխազդեցությանը չեզոք ատոմներում։
Բարձրէներգետիկ ռեակցիաների ուժեղ փոխազդեցություններ[խմբագրել | խմբագրել կոդը]
Գոյություն ունեն հադրոնների բախումների բարձրէներգետիկ պրոցեսների մի շարք, որոնցում բացակայում է կոշտ մասշտաբը, որի պատճառով, ՔՔԴ-ի շրջանակներում, հաշվարկները ըստ խոտորման տեսության դառնում են ոչ հավաստի։ Այդպիսի ռեակցիաների շարքում են հադրոնների լրիվ կտրվացքով բախումները, նրանց կոշտ ցրումը ոչ մեծ անկյուններով, դիֆրակցիոն պրոցեսները։ Կինեմատիկայի տեսանկյունից, այսպիսի ռեակցիաներում բախվող մասնիկների էներգիան է համարվում առավելագույնը հանգստի վիճակում, և ոչ սահմանային իմպուլսը։ Սկսած 1960-ական թվականներից, այսպիսի ռեակցիաների հիմնական հատկություններ հաջողությամբ նկարագրվել են Ռեջեյի տեսության վրա հիմնված ֆենոմենոլոգիական մոտեցումներով։ Այս տեսության շրջանակներում, հադրոնների ցրման բարձրէներգետիկ վիճակները առաջանում են որոշակի հավաքական օբյեկտների՝ ռեջեոնների փոխանակման արդյունքում։ Առավել կարևոր ռեջեոնը այս տեսության մեջ պոմերոնն է՝ միակ ռեջեոնը, որի ավանդը ցրման կտրվացքում չի փոքրանում էներգիայի հետ։ 1970-ական թվականներին պարզվեց, որ ռեջեոնների շատ հատկություններ կարելի է դուրս բերել քվանտային քրոմոդինամիկայից։ ՔՔԴ-ի համապատասխան մոտեցումը կոչվում է Բալիցկիի-Ֆադինի-Կուրաևի-Լիպատովի մոտեցում (ԲՖԿԼ)։
Ոժեղ փոխազդեցությունների տեսության ընթացիկ վիճակներ[խմբագրել | խմբագրել կոդը]
Ուժեղ փոխազդեցությունների տեսական նկարագիրը հանդիսանում է տարրական մասնիկների ֆիզիկայի ամենից շատ մշակված և դրա հետ մեկտեղ հախուռն կերպով զարգացած բաժիններց մեկը։ Չնայած նրան, որ քվարկների և գլյուոնների միջև ընթացող գունային փոխազդեցության հիմնական բնույթը հասկանալի է, քվանտային քրոմոդինամիկայով նրանց էությունը նկարագրող մաթեմատիկական հավասարումները բարդ ու խրթին են, այդ իսկ պատճառով կոնկրետ դեպքերում, առաջին սկզբուքից դրանց հաշվարկները դառնում են (համենայն դեպս, մինչ հիմա) անհնար։ Արդյունքում ծագում է էլեկտրական նկարագիր, երբ ճշգրիտ մաթեմատիկական հավասարումների կողքին հայտնվում են, քվանտոմեխանիկական ինտուիցիայի վրա հիմնված, կիսաքանակական մոտեցումներ, որոնք, սակայն հիանալի կերպով վերլուծում են էլեկտրամագնիսական տվյալները։ Նշենք ուժեղ փոխազդեցությունների ժամանակակից տեսության ընդհանուր կառուցվածքը։ Նախ և առաջ, տեսության հմքն է հանդիսանում քվանտային քրոմոդինամիկան։ Այս տեսության մեջ հիմնական ազատության աստիճանները քվարկներն ու գլյուոններն են, նրանց փոխազդեցության լագրանժիանը հայտնի է։ Ուժեղ փոխազդեցության նկարագրման մոտեցումները էականորեն կախված են այն բանից, թե կոնկրետ որ օբյեկտն է ուսումնասիրվում։ կարելի է առանձնացնել հետևյալ խմբերը՝
- կոշտ հադրոնային ռեակցիաներ, որոնցում հիմնական դեր են խաղում հենց այն քվարկներն ու գլյուոնները և որոնք լավ նկարագրվում են ՔՔԴ-ի խոտորման տեսությամբ,
- կիսակոշտ ռեակցիաներ, որոնցում գիտակից նկարագրման համար հարմար է հաշվի առնել խոտորման տեսության անվերջ թվով անդամներ, և որոշակի սահմանային դեպքերում դա հնարավոր դառնում իրագործել։
- ցածրէներգետիկ (փափուկ) հադրոնային ռեակցիաներ, որոնցում ազատության մակարդակները, առավել իմաստալից են դառնում քվարկները (հադրոնները) և ուսումնասիրվում են փոխազդեցության օրենքները։
- հադրոնների վիճակագրական հատկությունները, որոնցում, կախված կոնկրետ դեպքից, կարող են օգտագործվել տարբեր մոտեցումներ։
Ներքևում կարճ նկարագրված են ուժեղ փոխազդեցությունների տեսության մեթոդները յուրաքանչյուր դեպքի համար։
Հադրոնային կոշտ ռեակցիաներ[խմբագրել | խմբագրել կոդը]
Մինչ այժմ հայտնագործված բոլոր հադրոնները տեղաբաշխված են ստանդարտ նկարագրության մեջ, որում նրանք հավաքական՝ քվարկներից ու հադրոններից կառուցված, անգույն մասնիկներ են։ Այս ներքին քվարկային կառուցվածքի վրա հիմնված բնութագրիչ էներգիաները (այսինքն, պոտենցիալային մոդելների կապի էներգիաները) մոտավորապես ԳէՎ-ի կարգի են։ Ծագում է հադրոնների բախման պրոցեսների բնական դասակարգումը՝
- եթե իմպուլսի փոխանցումը -ից էականորեն փոքր է, ապա հադրոնների ներքին ազատության մակարդակների դինամիկան էական չէ, և կարելի է տեսությունը ապաձևակերպել հադրոնային էֆեկտիվ տեսության տեսքով։
- իսկ եթե ցրման ժամանակ իմպուլսի փոխանցումը էականորեն մեծ է այդ արժեքից, ապա խոսք է գնում կոշտ հադրոնային ռեակցիայի մասին։
Այս դեպքում հադրոնները մեծ ճշգրտությամբ պետք է համարել թույլ կապված, և ցրումը, առանձին արագ շարժվող հավաքական հադրոնների միջև տեղի է ունենում պարտոններով։ Այսպիսի վարքը կոչվում է ասիմպոտիկ ազատություն և կախված է, հիմնականում, իմպուլսի փոխանցման ժամանակ, ուժեղ փոխազդեցության հաստատունի նվազումից (հիմնականում հենց այս հայտնագործության համար է 2004 թվականին տրվել Նոբելյան մրցանակ ֆիզիկայի բնագավառում)։
Փարթոնային պատկեր[խմբագրել | խմբագրել կոդը]
Մեծ էներգիայով օժտված հադրոնը շնորհիվ ասիմպտոտիկ ազատության կարելի է համարել թույլ փոխազդեցությամբ օժտված մասնիկների համակարգ, որոնք շատ մոտենալու դեպքում չեն փոխազդում և ստացել են փարթոն անվանումը։ Ա և Բ հադրոնների փոխազդեցությունը դիտարկվում է որպես երկու փարթոնների փոխազդեցություն (համապատասխանաբար i և j): Նման ռեակցիայի ընթացքը կգրվի հետևյալ կերպ.
Այստեղ նշանակում է i տիպի փարթոնի խտությունը Ա հադրոնում, որը փոխադրում է հադրոնի իմպուլսի մի մասը։ Կոմպլիներային ֆակտորի էության մոտավոր նշանակությունն այն է, որ փարթոնների խտությունը այս արտահայտության մեջ կախված է նրանից, թե ինչ ռեակցիա ենք դիտարկում, իսկ երկու փարթոնների բախման գրանցման ժամանակ երկու փարթոնները համարվում են իրական (և ոչ վիրտուալ)։ Այդպիսի մոտեցումը լավ է աշխատում հենց կոշտ փոխազդեցության ոլորտում։
Բարձր էներգիայով հադրոնների փարթոնային կառուցվածքը ավելի բարդ է հենց նույն հադրոնների քվարկային կառուցվածքից, որոնք գտնվում են դադարի վիճակում։ Դադարի վիճակում գտնվող հադրոնի փոխակերպումը արագացման դեպքում ոչ միայն փոխվում է վալենտական քվարկների իմպուլսի բաժանումով, այլ նաև առաջանում են գլյուոններ, նաև քվարկի հակաքվարկ զույգեր (այսպես կոչված «ծովային քվարկներ»)։
Բոլոր այդ փարթոնները հադրոնի գումարային իմպուլսում ունեն իրենց բաժինը, նաև ունեն ներդրում հադրոնի ընդհանուր սպինում։ Արդեն մի քանի ՋԷՎ էներգիայով հադրոններում գլյուոնները տեղափոխում են հադրոնի իմպուլսի մոտավորապես կեսը և էներգիայի հետագա մեծացման հետ այդ բաժինը աճում է։
Փարթոնային խտությունների էվոլյուցիայի հավասարումներ[խմբագրել | խմբագրել կոդը]
Դինամիկ կապված համակարգը (իսկ ավելի ճշգրիտ, նրա վիճակի ֆոկովյան վեկտորը) ինվարիանտ չէ Լորենցի ձևափոխությունների համար, այդ պատճառով հաշվարկի այլ համակարգ տեղափոխվելիս, մենք դիտում ենք հադրոնի կազմի փոփոխություն; Կարելի է պայմանականորեն ասել, որ գլյուոնային կոմպոնենտը առաջանում է այն ուժից, որը պահում էր քվարկին բարձր էներգիաների դեպքում, հանգստի վիճակում գտնվող հադրոնում։ սրանից պարզ է դառնում, որ պարտոնային խտությունները առաջին սկզբունքներով հաշվարկելու համար, առայժ հնարավոր չէ, քանի որ ՔՔԴ-ում դեռևս լուծված չէ կապված վիճակների համընդհանուր պրոբլեմը։ Սակայն խոտորման տեսության սահմաններում ՔՔԴ կարելի է ներմուծել պարտոնային խտությունների էվոլյուցիայի հավասարումները՝ կոշտ պարամետրի մեծացմանը զուգընթաց (որպես օրենք, փոխանցված իմպուլսի քառակուսին)։ Այս հավասարումը կրում է Դոկշիցեր-Գրիբով-Լիպատով-Ալտարելլ-Պարիզի հավասարում (ԴԳԼԱՊ հավասարում) անվանումը։
Քվանտային քրոմոդինամիկան վանդակով[խմբագրել | խմբագրել կոդը]
Քվանտային քրոմոդինամիկան վանդակով՝ քվանտոքրոմոդինամիկ հաշվարկների ոչպերդուրպանցիոն (վայրիվեյրո փոփոխություններ) մոտեցում է, հիմնված անընդհատ տարածություն-ժամանակի փոխարինմամբ դիսկրետ վանդակով և, Մոնտե-կառլոյի մեթոդով, ընթացիկ պրոցեսների մոդելավորմամբ։ Այսպիսի հաշվարկները պահանջում են հզոր սուպերհամակարգիչներ, սակայն թույլատրում են առավել մեծ ճշգրտությամբ պարամետրերը հաշվարկել, որոնց հաշվարկը անալիտիկ այլ մեթոդներով հնարավոր չէ։ Օրինակ, պրոտոնի զանգվածի հաշվարկը տվել է իրականից 2 % փոքր մեծություն[2][3]։ Վանդակով ՔՔԴ-ն նույնպես թույլատրում է ընդունելի ճշգրտությամբ հաշվարկել այլ մասնիկների զանգվածները նույնպես, այդ թվում նաև դեռևս չբացահայտված հադրոններինն էլՙ որն էլ հեշտացնում է նրանց հայտնագործումը։ 2010 թվականին, վանդակային հաշվարկներով, u և d քվարկների զանգվածը կտրուկ կերպով ճշգրտվել է՝ հաշվարկի սխալը իջեցվելով 30 %-ից 1,5 %-ի[4]։
Հատկություններ[խմբագրել | խմբագրել կոդը]
Բացահայտված են ուժեղ փոխազդեցության մի շարք օրինաչափություններ։ Այսպես, ուժեղ փոխազդեցությունն ինվարիանտ է տարածական ինվերսիայի, ժամանակի անդրադարձման և լիցքային համալուծության նկատմամբ։ Ուժեղ փոխազդեցությամբ պայմանավորված պրոցեսներում պահպանվում են էլեկտրական և բարիոնային լիցքերը, տարօրինակությունը, հմայքը և գեղեցկությունը։ Բնության մեջ գոյություն ունեցող ուժեղ փոխազդող մասնիկները՝ հադրոնները, կարելի է բաժանել խմբերի, որոնցից յուրաքանչյուրի մեջ մտնում են մոտավորապես հավասար զանգված և միևնույն ներքին քվանտային թվեր (բացառությամբ էլեկտրական լիցքի) ունեցող մասնիկներ։ Այդ խմբերը կոչվում են ՏՍ(2) իզոտոպային խմբի իզոտոպային մուլտիպլետներ։ Օրինակ, պրոտոնը և նեյտրոնը կազմում են իզոտոպային դուպլետ, իսկ π+-, π0- և π--մեզոնները՝ իզոտոպային տրիպլետ։ Ուժեղ փոխազդեցությունն ունի իզոտոպային ինվարիանտության հատկություն՝ մի մուլտիպլետ կազմող մասնիկների ուժեղ փոխազդեցությունը նույնն է։ Հետևյալ քայլը տարբեր իզոտոպային մուլտիպլետներին պատկանող և տարօրինակության տարբեր արժեք ունեցող հադրոնների խմբավորումն է ըստ ՏՍ (3) ունիտար խմբի մուլտիպլեաների։ Օրինակ, պրոտոնը, նեյտրոնը և Λ--, Σ+-, Σ0-, Σ--, Ξ0-, Ξ--հիպերոնները կազմում են ունիտար օկտեա։ Հադրոնները դասակարգելիս պարզորոշ դրսևորվում է ևս մեկ օրինաչափություն։ Միևնույն ներքին քվանտային թվեր ու տարբեր սպիններ ունեցող մասնիկները կազմում են I~M2 ուղիղ գծերի վրա դասավորվող շարքեր (I-ն մասնիկի սպինն է, M-ը՝ զանգվածը)։ Այդ գծերը կոչվում են Ռեջեի հետագծեր (իտալացի ֆիզիկոս Տ․ Ոեջեի)։ Ուժեղ փոխազդեցության հատկությունների հետազոտման փորձերը ցույց են տվել, որ բարձր էներգիաների դեպքում հադրոնների ուժեղ փոխազդեցության լրիվ կտրվածքների բնորոշ արժեքներն ընկած են 20-25 մբառն (մեզոն-նուկլոնային փոխազդեցություններ) և 40-45 մբառն (նուկլոն-նուկլոնային փոխազդեցություններ) տիրույթներում և դրսևորում են էներգիայի հետ դանդաղ աճի միտում։ Բարձր էներգիայի հադրոնների բախումներում հիմնական մասը (~80%) կազմում են բազմակի ծնման պրոցեսները։ Այդ պրոցեսներում ծնված մասնիկների բաշխումներն ըստ երկայնական իմպուլսի (P||), բախման տարբեր էներգիաների (E) դեպքում նման են և կախված են միայն P||E հարաբերությունից։ Այդպիսի վարքագիծը կոչվում է Ֆեյնմանի սկեյլինգ կամ մասշտաբային ինվարիանտություն (անգլ.՝ scaling մասշտաբավորում)։ Ուժեղ փոխազդեցության հետևանքով ծնված մասնիկների լայնական իմպուլսների () արժեքները սահմանափակ են ( ≈^0,3—0,5 ԳէՎ/c) և փաստորեն կախված չեն E-ից։ -ի մեծ արժեք ունեցող մասնիկների ծնունդը խիստ հազվադեպ է և հաստատում է հադրոնների փարթոնային պատկերացումները, որոնք առաջացել են լեպտոն-նուկլոնային ոչ առաձգական ցրման պրոցեսներն ուսումնասիրելիս։ Ուժեղ փոխազդեցության տեսական հետազոտություններում լայնորեն կիրառվում են պրոցեսների ամպլիտուդների ընդհանուր հատկությունների (պատճառականություն, խաչաձև սիմետրիա) վրա հիմնված մոդելները։ Անալիտիկությունը պատճառականության հետևանք է ամպլիտուդների՝ որպես իրենց փոփոխականների ֆունկցիաների։ Վերջինս իր հերթին հանգեցնում է ամպլիտուդների իրական ու կեղծ մասերն իրար կապող դիսպերսիոն առնչությունների։ Բարձր էներգիայի հադրոնների ուժեղ փոխազդեցությունը նկարագրող տեսական մոդելներից ամենալայն ճանաչումն ստացել է Ռեջեի բևեռների (ռեջեոնների) մեթոդը (ՌԲՄ)։ Այդ մեթոդի հիմքում ընկած է այն պատկերացումը, որ ցրման պրոցեսում մասնիկները փոխանակվում են փոփոխական սպին և զանգված ունեցող յուրահատուկ հադրոնային կոմպլեքսներով՝ Ոեջեի բևեռներով (հետագծերով)։ Դրանով իսկ խոր կապ է բացահայտվում ցրման պրոցեսների և Ռեջեի հետագծերի միջև։ ՌԲՄ-ն թույլ է տալիս դասակարգել ու նկարագրել ինչպես երկմասնիկ, այնպես էլ բազմամասնիկ պրոցեսների ամենատարբեր հատկություններ։ Փորձով հաստատվել են Ռեջեի մի շարք հետագծեր՝ մեզոնային (օրինակ, ρ-, ω-, Λ, ք-, π- հետագծերը), բարիոնային (N-,Δ- հետագծերը և այլն), և, այսպես կոչված, պոմերոնը։ Վերջինս տեսություն է ներմուծվել լրիվ կտրվածքների էներգիայից կախումն բացատրելու համար։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Бете Г., Моррисон Ф. Элементарная теория ядра. — М: Иностранная литература, 1958. — С. 207—209. — 352 с.
- ↑ S. Dürr, Z. Fodor, J. Frison, C. Hoelbling, R. Hoffmann, S. D. Katz, S. Krieg, T. Kurth, L. Lellouch, T. Lippert, K. K. Szabo, and G. Vulvert (2008 թ․ նոյեմբերի 21). «Ab Initio Determination of Light Hadron Masses». Science. 322 (5905): 1224. Bibcode:2008Sci...322.1224D. doi:10.1126/science.1163233. PMID 19023076.
{{cite journal}}: More than one of|pages=and|page=specified (օգնություն)CS1 սպաս․ բազմաթիվ անուններ: authors list (link) - ↑ «Учёные подтвердили знаменитую формулу Эйнштейна». Membrana. 2008 թ․ նոյեմբերի 24. Արխիվացված օրիգինալից 2012 թ․ մայիսի 27-ին. Վերցված է 2012 թ․ մարտի 1-ին.
- ↑ «Легчайшие кварки взвешены с невероятной точностью». Membrana. 2010 թ․ ապրիլի 7. Արխիվացված օրիգինալից 2012 թ․ մայիսի 27-ին. Վերցված է 2012 թ․ մարտի 1-ին.
Գրականություն[խմբագրել | խմբագրել կոդը]
- Фейнман Р․, Взаимодействие фотонов с адронами, пер․ с англ․, М․, 1975;
- Глэшоу Ш․, Кварки с цветом и ароматом, «Успехи физических наук», 1976, т․ 119, в․ 4;
- Намбу Ё․, Кварки, пер․ с японского, М․, 1984․
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից։ |
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- Д.И. Вайсбурд — ISBN 978-5-98298-665-8, УДК 53 (075.8), ББК 22. 3я73 (2010 год). «Общая физика.Нетрадиционный курс» (PDF). lib.tpu.ru и Издательство Томского политехнического университета. էջեր С. 33-34, 62–63. Արխիվացված (PDF) օրիգինալից 2012 թ․ դեկտեմբերի 1-ին. Վերցված է 30.11.2012-ին.
- Артур Давидович Чернин — ISBN 5275016131, 9785275016130, УДК 52, ББК 22,61, 318 страниц всего (2008 год). «Физика времени». Google и Издательство Терра. էջեր С. 149. Վերցված է 10.12.2012-ին.
- J.R. Christman (2001). «MISN-0-280: The Strong Interaction» (PDF). на сайте Project PHYSNET. Արխիվացված (PDF) օրիգինալից 2011 թ․ օգոստոսի 22-ին. Վերցված է 2018 թ․ սեպտեմբերի 20-ին.
{{cite web}}: External link in|work= - Видео Лекции: Теория электрослабых взаимодействий (профессор Черняк В. Л., 2013 г.)







































