Գերհոսուն հելիում-4

Գերհոսուն հելիում-4 (անգլ.՝ superfluid helium-4), հելիում տարրի 4 զանգվածով իզոտոպի ֆազային վիճակ, որում այն ցուցաբերում է 0-ական մածուցիկությամբ հեղուկի հատկություններ․ հոսում է առանց շփման ցանկացած մակերևույթով, թափանցում է շատ փոքր անցքերով՝ ենթարկվելով միայն իր սեփական իներցիային։ Հելիումի գերհոսուն վիճակը դիտվում է այն դեպքում, երբ այն սառեցվում է կրիտիկական ջերմաստիճանից ցածր (~2,17 Կ)։ 1 Կ ջերմաստիճանում այն գրեթե ամբողջությամբ դառնում է գերհոսուն։

Գերհոսուն հելիումը հայտնի է որպես քվանտային հիդրոդինամիկայի և մակրոսկոպիկ քվանտային երևույթների ուսումնասիրման հիմնական օբյեկտ։ Գերհոսունության առաջացումը համարվում է ավարտված Բոզե-Այնշտայնի կոնդենսատի ձևավորմամբ։ Դրա համար ապացույց է հանդիսանում այն փաստը, որ հելիում 4-ի գերհոսունությունը հեղուկ վիճակում դիտվում է ավելի բարձր ջերմաստիճաններում, քան այն կարելի է դիտել հելիում-3 իզոտոպում։ Հելիում 4-ի յուրաքանչյուր ատոմ բոզոն է, քանի որ նրա սպինը հավասար է 0-ի։ Այնուամենայնիվ, հելիում 3-ը ֆերմիոն է, որը կարող է ստեղծել բոզոններ միայն նմանատիպ ատոմի հետ զուգակցվելով ավելի ցածր ջերմաստիճաններում, գերհաղորդականության երևույթի մեջ էլեկտրոնների զուգակցման նման մի գործընթացում։ Հելիում 4-ի իզոտոպը (⁴He) մոտավորապես միլիոն անգամ ավելի տարածված է, քան հելիում 3-ը (³He) , այդ պատճառով, երբ խոսք է գնում հելիումի գերհոսունության կիրառման մասին, հիմնականում նկատի է առնվում հենց ⁴He-ը։ ³He-ի ոչ մեծ քանակությամբ խառնուրդները ⁴He-ի հատկությունները չեն ցուցաբերում. ձևավորվում է լուծույթ, որը պահպանում է գերհոսունությունը, չնայած անցման ջերմաստիճանը նվազում է։ ³He-ի մեծ կոնցենտրացիայիով լուծույթները դեռևս լավ չեն ուսումնասիրված։

Ներկայում բացի հեղուկ հելիումից, որին բնորոշ է հոսունության վիճակը, կա այդպիսի հատկությամբ օժտված ջրածին (շատ քիչ քանակությամբ՝ մի քանի տասնյակ մոլեկուլ, քանի որ օրթո- և ջրածնի մոլեկուլները լավ խառնվում են նույնիսկ շատ ցածր ջերմաստիճանում)։

Հետազոտության պատմություն

Հեղուկացված հելիումն առաջին անգամ ստացել է Կամերլինգ Օնեսը 1908 թվականի հուլիսի 10-ին։ Դրա համար անհրաժեշտ էր գազը սառեցնել մինչև 4Կ ջերմաստիճան։ 1910 թվականին Կեմերլինգ-Օնեսը կարողացել է սառեցնել հելիումը մինչև 1,04 Կ ջերմաստիճան։ Այս հետեզոտությունների համար նա 1913 թվականին արժանացել է Նոբելյան մրցանակի։ Հեղուկացված հելիումը մինչև 1 Կ հնարավոր է սառեցնել ցածր ճնշման տակ գոլորշիացնելով (վակումային պոմպի կիրառմամբ)։

Հեղուկացված հելիումի գերհոսունությունը հայտնաբերել են Պյոտր Կապիցան, Ջոն Ալենը և Դոն Միսեները 1937 թվականին։ Այդ ժամանակվանից այն նկարագրվել է ֆենոմենոլոգիական և մանրադիտակային տեսությունների միջոցով։

1950-ական թվականներին Հոլլը (Hall H.E.) և Վայնենը (Vinen W.F.) իրականացրել են փորձեր, որոնք հասատատել են քվանտային պտույտային գծերի առկայությունը գերհոսուն հելիումում։ 1960-ական թվականների Ռեյֆիլդը (Rayfield) և Ռիֆը (Reif) հաստատել են քվանտային պտույտային օղակների առկայությունը։ Պակարդը (Packard) նկատել է պտույտային գծերի հատումը հեղուկի ազատ մակերեսին, Ավենելը (Avenel) և Վերոկուն (Varoquaux) ուսումնասիրել են Ջոզեֆսոնի էֆեկտը գերհոսուն հելիում 4-ում։ 2006 թվականին Մերիլենդի համալսարանի մի խումբ գիտնականներ վիզուալացրել են քվանտային պտույտները ծանր ջրածնի մարկերային մասնիկների միջոցով։

21-րդ դարում

2000-ականներին սկզբին ֆիսիկոսներն ստեղծել են ֆերմիոնային կոնդենսատ՝ ֆերմիոնների գերսառը ատոմների զույգերից։ Որոշակի պայմաններում ֆերմիոնի ատոմային զույգերը ձևավորում են երկատոմ մոլեկուլներ, և համակարգում հնարավոր է դառնում Բոզե-Այնշտայնի խտացումը։ Մյուս ծայրահեղությունում ֆերմիոնները (մասնավորապես գերհաղորդիչ էլեկտրոնների մեծ մասը) ձևավորում են կուպերովյան զույգեր, որոնց նույնպես բնորոշ է գերհոսունությունը։ Գերսառը ատոմային գազերի վերաբերյալ այս աշխատանքը հնարավորություն է տվել ուսումնասիրել այս երկու ծայրահեղությունների միջև ընկած տարածքը, որը հայտնի է որպես BEC-BCS քրոսովեր։

Գերհոսուն պինդ մարմինները, հնարավոր է, հայտնաբերվել են 2004 թվականին Փենսիլվանիա նահանգի համալսարանի ֆիզիկոսների կողմից։ Եթե հելիում-4-ը սառեցվի 200մԿ ջերմաստիճանից ցածր ջերմաստիճանում բարձր ճնշման տակ, պինդ մարմնի մոտավորապես մեկ տոկոսը դառնում է գերհոսուն։ Տորսիոնային օսցիլյատորի օգնությամբ կատարված փորձով ցույց է տրվել, որ կտրուկ սառեցման կամ կարգավորման ժամանակահատվածի երկարաձգման (դրանով իսկ բարձրացնելով կամ նվազեցնելով թերությունների խտությունը համապատասխանաբար) դեպքում գերհոսուն պինդ մարմնի ֆրակցիան կարող է լինել 20 %-ից մինչև բոլորովին բացակայող։ Սա հնարավորություն է տվել ենթադրել, որ գերհոսուն պինդմարմնային հելիում 4-ի հատկությունները բնորոշ չեն հելիում 4-ին և կարգավորված չեն։

Հատկություններ

Նկար 1. ⁴He ֆազային դիագրամ։ Ցույց է տալիս, թե ինչպիսի պայմաններում (ջերմաստիճան (Т) և ճնշում (р) է հելիումը գտնվում գազային, հեղուկ և պինդ վիճակներում։ Ֆազային դիագրամում համապատասխան հատվածները բաժանվում են հալման կորով (հեղուկ և պինդ վիճակների միջև) և եռման գծով (հեղուկ և գազային վիճակների միջև)։ Վերջին գիծն ավարտվում է կրիտիկական կետում, որտեղ գազի և հեղուկի միջև տարբերությունը անհետանում է։

Նկար 2. Հեղուկ ⁴He-ի ջերմունակությունը հագեցած գոլորշիների ճնշման տակ, որպես ջերմաստիճանային ֆունկցիա։ Ամենաբարձր կետը T = 2,17 Կ-ի դեպքում նշանակում է երկրորդ կարգի ֆազային անցում։

Նկար 3. Նորմալ և գերհոսուն համակարգերի հարաբերական կախվածությունը ջերմաստիճանից ρ_n/ρ і ρ_s/ρ, որպես ֆունկցիա T

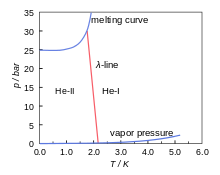
Վիճակի դիագրամը (նկար 1) ցույց է տալիս ⁴He-ի յուրահատկությունը, որը կարող է գտնվել հեղուկ վիճակում նույնիսկ բացարձակ 0-ի դեպքում։ Այն կարծրանում է միայն ավելի քան 25 բար ճնշման տակ։

Այդ դիագրամում նաև ցույց է տրված λ-գիծը, որը բաժանում է հեղուկ վիճակի երկու տարածքը, որոնք նշանակված են He-I և He-II։ He-I-ի տարածքում հելիումն իրեն դրսևորում է որպես նորմալ հեղուկ, իսկ He-II-ում՝ գերհոսուն։

Լամբդա գծի անվանումը ծագում է յուրահատուկ գրաֆիկից, որը ցույց է տալիս ջերմունակության կախվածությունը ջերմաստիճանից, ինչը հիշեցնում է հունական λ (լյամբդա) տառը։ Ջերմունակության գագաթնակետը դիտվում է 2,172 Կ ջերմաստիճանում (նկար 2), որը կոչվում է λ-կետ։

Լամբդա գծից ներքև հելիումի վարքագիծը հնարավոր է ֆենոմենոլոգիականորեն նկարագրել այսպես կոչված երկհեղուկային մոդելի միջոցով։ Այն իրեն պահում է այնպես, կարծես բաղկացած է երկու բաղադրիչներից՝ նորմալ, որը նման է սովորական հեղուկի և գերհոսուն՝ 0-ական մածուցիկությամբ և 0-ական էնտրոպիայով։ Նորմալ (ρ_n) և գերհոսուն (ρ _s) բաղադրիչների խտությունների հարաբերությունը կախված է ջերմաստիճանից և ներկայացված է նկար 3-ում։ Ջերմաստիճանի նվազման դեպքում գերհոսուն (ρ_s/ρ) բաղադրիչի խտությունը բարձրանում է 0-ից T _λ մինչև 1-ի Կելվինով 0-ական ջերմաստիճանի դեպքում։ 1 Կ-ից ցածր ջերմաստիճանում հելիումը գրեթե ամբողջությամբ գերհոսուն է։ 0,7 Կ-ից ցածր ջերմաստիճանում նորմալ բաղադրիչների խտության կախվածությունը ջերմաստիճանից ունի ρ_n ~ T⁴ տեսքը։

Կարելի է ստեղծել նորմալ բաղադրիչի (և հետևաբար գերհոսուն բաղադրիչի, քանի որ ρ_n + ρ_s = հաստատուն), որոնք հիշեցնում են սովորական ձայնային ալիքներ։ Այս էֆեկտը կոչվում է երկրորդ ձայն։ ρ_n ջերմաստիճանային կախվածության միջոցով (նկար 3) ρ_n-ում այս ալիքները նաև ջերմաստիճանային ալիքներ են։

Նկար 4. Հելիում II «սողում է» մակերևույթով, և որոշ ժամանակ անց երկու տարաների մակարդակները կհավասարվեն։ Ռոլլինի թաղանթը ներառում է մեծ տարայի ներքին մասը, եթե այն կնքված չլինի, ապա հելիում II-ը կհոսի և կթափվի։

Նկար 5. Գավաթի ներսում հեղուկ հելիումը գտնվում է գերհոսուն վիճակում։ Քանի դեռ գերհոսուն է, այն սողում է գավաթի պատի վրայով դեպի վեր բարակ թաղանթի տեսքով։ Այս թաղանթը հոսում է եզրերով, իսկ այնուհետև իջնում է արտաքին կողմով՝ հատակին առաջացնելով հեղուկի կաթիլ։ Կաթիլները ձևավորվում են մեկը մյուսի հետևից, մինչև գավաթը ամբողջությամբ դատարկվի։

Թաղանթի հոսք

Բազմաթիվ սովորական հեղուկներ, ինչպիսիք են սպիրտը և նավթը, կոշտ պատի վրայով կսողան դեպի վեր թրջման երևույթի շնորհիվ, ինչը պայմանավորված է մակերևույթային լարվածությամբ։ Հեղուկ հելիումը նույնպես ունի այս հատկությունը, սակայն He-II-ի դեպքում շերտում հեղուկի հոսքը սահմանափակվում է ոչ միայն նրա մածուցիկությամբ, այլ մոտ 20 սմ/վրկ կրիտիկական արագությամբ։ Դա բավականին մեծ արագություն է, այդ պատճառով գերհոսուն հելիումը կարող է հեշտությամբ հոսել դեպի վեր դատարկ տարայի պատերի վրայով, որոնք մասամբ ընկղմված են հեղուկի մեջ, հոսել մինչև վերին եզրը և դուրս հոսում՝ լցնելով տարան մինչև հեղուկի մակարդակը դրսից։ Այս սիֆոնային էֆեկտը սխեմատիկ կերպով ցույց է տրված նկար 4-ում։ Եթե լցված տարան բարձրացնենք հեղուկի մակարդակից վեր, ապա տարայի հատակին թաղանթի հոսքը կառաջացնի տեսանելի կաթիլներ, ինչպես ցույց է տրված նկար 5-ում։

Տարբերությունը հելիում 3-ից

Չնայած հելիում 3-ի և հելիում 4-ի գերհոսունության ֆենոմենոլոգիաները շատ նման են, սակայն անցումների մանրադիտակային մանրամասները զգալիորեն տարբերվում են։ Հելիում 4-ի ատոմները բոզոններ են, և դրանց գերհոսունությունը կարելի բացատրել Բոզե-Այնշտայնի վիճակագրության միջոցով, որին նրանք ենթարկվում են։ Մասնավորապես, հելիում 4-ի գերհոսունությունը կարելի բացատրել Բոզե-Այնշտայնի խտացման միջոցով, որին նրանք ենթարկվում են։ Մյուս կողմից, հելիում 3-ի ատոմները ֆերմիոններ են, և գերհոսունության անցումը այս համակարգում բացատրվում է ԲԿՇ գերհաղորդականության տեսության ընդհանրացմամբ։ Այս տեսության համաձայն՝ ատոմների միջև տեղի է ունենում կուպերովյան զուգավորում (այլ ոչ թե էլեկտրոնների միջև, ինչպես ԲԿՇ դեպքում) և դրանց միջև ձգողականության փոխազդեցությունը փոխանցվում է սպինային, այլ ոչ թե ֆոնոնի տատանումների միջոցով։ Գերհաղորդականության և գերհոսունության համակցված վիճակը կարելի է նկարագրել համակարգի չափիչ համաչափության հանկարծակի խախտման տեսանկյունից։

Երկկոմպոնենտություն

Գերհոսուն հեղուկները, ինչպիսին է հելիում 4-ը լամբդայի կետից ցածր, ունեն մեծ թվով անսովոր հատկություններ։ Գերհոսունությունը գործում է այնպես, կարծես հեղուկը գերհոսուն բաղադրիչի և սովորական հեղուկի խառնուրդ է։ Գերհոսուն բաղադրիչն ունի զրոյական մածուցիկություն և էնտրոպիա։ Համակարգ ջերմության ներմուծումը հանգեցնում է նորմալ բաղադրիչի հոսքին, որն ապահովում է է ջերմության փոխանցումը բավականին մեծ արագությամբ (մինչև 20 սմ/վրկ), ինչը հանգեցնում է շատ բարձր ջերմահաղորդականության։

Քվանտային պտույտներ

Հիմնական հատկություններից մեկն էլ դրսևվորվում է, եթե գերհոսուն հեղուկը տեղադրվի ցենտրիֆուգում (պտտվող տարա)։ Ցենտրիֆուգի հետ պտտվելու փոխարեն հելիումում առաջանում են քվանտային պտույտներ։ Այսինքն, երբ սարքը պտտվում է առաջին անկյունային արագությունից ցածր արագությամբ, հեղուկը ամբողջությամբ մնում է անշարժ։ Այն բանից հետո, երբ արագությունը հասնում է առաջին անկյունայինին, գերհոսուն հեղուկն առաջացնում է պտույտներ։ Պտույտների ուժը քվանտային է, այսինքն՝ գերհոսուն հեղուկը կարող է պտտվել միայն անկյունային արագության որոշակի «թույլատրելի» արժեքների դեպքում։ Նորմալ հեղուկի պտտումը, ինչպիսին է ջուրը, չի քվանտացվում։ Եթե պտտման արագությունն էլ ավելի մեծանա, կձևավորվեն նոր քվանտային պտույտներ՝ առաջացնելով հետաքրքիր նախշեր, որոնք նման են Աբրիկոսովի ցանցին գերհաղորդիչներում։

Գերհոսուն հիդրոդինամիկա

Գերհոսուն բաղադրիչի շարժման հավասարումը, մի քանի անգամ պարզեցված ձևով, ենթարկվում է Նյուտոնի օրենքին.

${\vec {F}}=M_{4}{\frac {\mathrm {d} {\vec {v}}_{s}}{\mathrm {d} t}}$

M₄ ⁴He-ի մոլային զանգվածն է, և ${\vec {v}}_{s}$՝ գերհոսուն բաղադրիչի արագությունը։ Ժամանայկի ածանցյալը՝ այդպես կոչված հիդրոդինամիկ ածանցյալը, այսինքն՝ գրանցված է հեղուկի տարրի համար, որը ինքնուրույն շարժվում է։ Գերհոսուն ⁴He-ի դեպքում գրավիտացիոն դաշտում ուժը դրսևորվում է ինչպես.

${\vec {F}}=-{\vec {\nabla }}(\mu +M_{4}gz)$

Այս հավասարումում μ-ը քիմիական մոլային պոտենցիալն է, g-ը՝ գրավիտացիոն արագացումը, իսկ z-ը՝ կոորդինատի ուղղահայացը։ Այսպիսով.

$M_{4}{\frac {\mathrm {d} {\vec {v}}_{s}}{\mathrm {d} t}}=-{\vec {\nabla }}(\mu +M_{4}gz)$ (1)

(1) հավասարումը իրականացվում է միայն այն դեպքում, երբ v_s-ը չի գերազանցում կրիտիկական արժեքը, որը, որպես կանոն, որոշվում է հոսքի ալիքի տրամագծով։

Դասական մեխանիկայում ուժը հաճախ հանդիսանում է պոտենցիալ էնորգիայի կրող։ Հավասարում (1)-ը ցույց է տալիս, որ գերհոսուն բաղադրիչի առկայության դեպքում ուժը կրում է արժեք, որն ուղիղ համեմատական է քիմիական պոտենցիալի գրադիենտին։ Դրա շնորհիվ He-II-ը դրսևորում է այնպիսի հրաշալի հատկություն, ինչպիսին է շատրվանային էֆեկտը։

Նկար 6. μ-ի ինտեգրման հաշվարկման ուղին p և T կամայականներով

Նկար 7. Շատրվանային ճնշման դրսևորում. եկու անոթները կապված են գերհոսքով, որի միջով հոսում է միայն գերհոսուն բաղադրիչը

Նկար 8. Շատրվանային էֆեկտի ցուցադրում. մազանոթային խողովակը մի ծայրում «փակվում է» գերհոսուն արտահոսքով և տեղավորվում գերհոսուն հելիումով բաղնիքի մեջ, այնուհետև տաքացվում է։ Հելիումը հոսում է խողովակի միջով և դուրս է ցայտում ինչպես շատրվան։

Շատրվանային ճնշում

(1) հավասարումն ավելի պարզ տեսքով վերաշարադրելու համար օգտագործվում է ընդհանուր բանաձև․

|$\mathrm {d} \mu =V_{m}\mathrm {d} p-S_{m}\mathrm {d} T$ (2)

Այստեղ S_m-ը մոլյար էնտրոպիան է, իսկ V _m-ը՝ մոլյար ծավալը։ 2-րդ հավասարման միջոցով μ(p,T)-ը կարելի է որոշել р-Т հարթության ստուգողական ինտեգրման միջոցով։ Նախ ինտեգրում ենք կոորդինատների սկզբնակետից (0,0) մինչև (p, 0), այսինքն՝ T = 0 դեպքում։ Այնուհետև ինտեգրում ենք (р, 0)-ից մինչև (p,T), այսինքն՝ մշտական ճնշմամբ (տես նկար 6)։ Առաջին ինտեգրալում dT = 0, իսկ երկրորդում՝ dp = 0։ (2) հավասարման միջոցով ստանում ենք․

|$\mu (p,T)=\mu (0,0)+\int _{0}^{p}V_{m}(p^{\prime },0)\mathrm {d} p^{\prime }-\int _{0}^{T}S_{m}(p,T^{\prime })\mathrm {d} T^{\prime }$ (3)

Մենք հետաքրքրված ենք միայն այն դեպքերով, երբ р-ն փոքր է, այնպես որ V _m-ը գրեթե չի փոխվում։ Հետևապես․

|$\int _{0}^{p}V_{m}(p^{\prime },0)\mathrm {d} p^{\prime }=V_{m0}p$ (4)

Որտեղ V _m0 հեղուկի մոլյար ծավալն է T = 0 և p = 0 պայմաններում։ (3) հավասարման մյուս անդամը նույնպես գրվում է որպես V_m0-ի ածանցյալ և p_f մեծությունը, որը ունի ճնշման չափ․

|$\int _{0}^{p}V_{m}(p^{\prime },0)\mathrm {d} p^{\prime }=V_{m0}p$ (5)

p_f ճնշումը կոչվում է շատրվանային ճնշում։ Այն կարելի է հաշվարկել հելիում 4-ի էնտրոպիայի միջոցով, որն իր հերթին կարելի է հաշվարկել ջերմունակության միջոցով։ T = T_λ-ի համար շատրվանային ճնշումը հավասար է 0,692 բար։ Հեղուկ հելիումի 125 կգ/մ³ խտության և g = 9.8 մ/սմ² դեպքում այդ ճնշումը համապատասխանում է 56 մ բարձրությամբ հեղուկ հելիումի սյան ճնշմանը։ Հետևաբար բազմաթիվ փորձերի մեջ շատրվանային ճնշումը ավելի մեծ ազդեցություն է ունենում գերհոսուն հելիումի շարժման վրա, քան ձգողության ուժը։

(4) և (5) հավասարումների օգնությամբ (3)ն հավասարումը ունենում է հետևյալ տեսքը․

|$\mu (p,T)=\mu _{0}+V_{m0}(p-p_{f})$ (6)

(6) հավասարման ներդրումը (1)-ի մեջ տալիս է․

|$\rho _{0}{\frac {\mathrm {d} {\vec {v}}_{s}}{\mathrm {d} t}}=-{\vec {\nabla }}(p+\rho _{0}gz-p_{f})$ (7)

Հեղուկ ⁴He-ի խտությամբ 0-ական ճնշման և ջերմաստիճանի պայմաններում ρ₀ = M ₄/V_m0։

Հավասարում (7)-ը ցույց է տալիս, որ բաղադրիչի գերհոսունությունն արագանում է, որպես կանոն գրավիտացիոն ձևով պայմանավորված ճնշման գրադիենտով, ինչպես նաև շատրվանային ճնշման գրադիենտով։

Դեռևս (5) հավասարումն ունի զուտ մաթեմատիկական նշանակություն, սակայն հատուկ փորձարարական պայմաններում p_f կարող է դրսևորվել որպես իրական ճնշում։ Նկար 7-ում ցույց են տրվում 2 անոթներ, որոնցում He-II է։ Ձախ անոթը պետք է գտնվի ըստ Կելվինի 0 աստիճանում (T_l = 0) և 0-ական ճնշման պայմաններում (p _l = 0)։ Անոթները միացված են այսպես կոչված գերհոսունության արտահոսքի միջոցով։ Դա խողովակ է, որը լցված է շատ մանր փոշով, որի պատճառով նոր բաղադրիչի հոսքը գրեթե արգելափակված է։ Այնուամենայնիվ գերհոսուն բաղադրիչը կարող է հոսել դրա միջով առանց որևէ խոչընդոտի ( կրիտիկական արագությունից ցածր՝ մոտավորապես 20 սմ/վ)։ Ստանդարտ պայմաններում v _s = 0, այդ պատճառով (7) հավասարումից հետևում է՝

|$p_{l}+\rho _{0}gz_{l}-p_{fl}=p_{r}+\rho _{0}gz_{r}-p_{fr}$ (8)

որտեղ l (r) ինդեքսը վերաբերում է ձախ (աջ) կողմի գերհոսունությանը։ Հետևյալ կոնկրետ դեպքում p_l = 0, z_l = z_r, և p _fl = 0 (քանի որ T _l = 0)։ Հետևաբար․

$0=p_{r}-p_{fr}$

Դա նշանակում է, որ աջ անոթի ճնշումը հավասար է շատրվանային ճնշմանը T_r դեպքում։

Շատրվանը կարելի է ստեղծել փորձի շնորհիվ, որը ներկայացված է նկար 8-ում։ Շատրվանային էֆեկտը օգտագործվում է ³He շրջանառության նպատակով լուծարման սառնարաններում։

Նկար 9. Ջերմության փոխադրումներ He-II-ի նորմալ և գերհոսուն բաղադրիչների հակահոսանքի օգնությամբ

Ջերմության փոխանցումը

Նկ․ 9-ում ցույց է տրվում T_H և T ջերմաստիճաններով երկու անոթների միջև ջերմության փոխանակուման փորձը, որոնք միացված ե He-II-ով լցված խողովակով։ Երբ ջերմությունը մատակարարվում է տաք վերջնամաս, այստեղ առաջանում է ճնշում (7) հավասարման համաձայն։ Այս ճնշումը ստիպում է նորմալ բաղադրիչին տեղաշարժվել տաք ծայրից դեպի սառը հետևյալ հավասարման համաձայն․

|$\Delta p=-\eta _{n}Z{\dot {V}}_{n}$ (9)

Այստեղ η_n-ը նորմալ բաղադրիչի մածուցիկությունն է, Z-ը՝ որոշակի երկրաչափական բազմապատկիչ, իսկ ${\dot {V}}_{n}$-ը՝ ծավալային հոսքը։ Նորմալ հոսքը հավասարակշռվում է գերհոսուն բաղադրիչի հոսքով սառը ծայրից դեպի տաք ծայրը։ Վերջնամասերում տեղի է ունենում վերափոխում, նորմալ բազադրիչը վերածվում է գերհոսունի և հակառակը։ Այսպիսով, ջերմությունը փոխանցվում է ոչ թե ջերմահաղորդականության, այլ կոնվեկցիայի միջոցով։ Ջերմահաղորդականության այս ձևը շատ արդյունավետ է, քանի որ He-II-ի ջերմահաղորդականությունը շատ ավելի մեծ է, քան լավագույն նյութերինը։ Իրավիճակը համեմատելի է ջերմահաղորդիչների հետ, որտեղ ջերմահաղորդականությունը տեղի է ունենում գազ-հեղուկ փոխարկման միջոցով։ He-II-ի բարձր ջերմահաղորդականությունն օգտագործվում է գերհաղորդիչ մագնիսների կայունացման համար, օրինակ՝ ՑԵՌՆ-ում Մեծ հադրոնային բախիչում։

Տեսություն

Լանդաուի երկհեղուկ մոտեցում

Լև Լանդաուն հելիում 4-ի ֆենոմենոլոգիական և կիսամանրադիտակային գերհոսունության տեսության համար 1962 թվականին արժանացել է ֆիզիկայի ասպարեզում Նոբելյան մրցանակի։ Ենթադրելով, որ ձայնային ալիքները ցածր ջերմաստիճանում հելիում-4-ի համար հանդիսանում են առավել կարևոր գրգռիչներ, նա ցույց է տվել, որ հելիում-4-ը, որը հոսում է պատի կողքով, հանկարծակի գրգռականություն չի առաջացնի, եթե հոսքի արագությունը ցածր է ձայնի արագությունից։ Այս մոդելում ձայնի արագությունը հանդիսանում է «կրիտիկական արագություն», որից բարձրում գերհոսունությունը քայքայվում է (հելիում 4-ը իրականում ունի հոսքի ավելի ցածր արագություն, քան լույսի արագությունն է)։ Լանդաուն նաև ցույց է տվել, որ ձայնային ալիքները և այլ խանգարումներ կարող են միմյանց հավասարակշռել և շարժվել անկախ հելիում 4-ի մնացած մասից, որը հայտնի է որպես «կոնդեսատ»։

Ելնելով գրգռման հոսքի իմպուլսից և արագությունից՝ Լանդաուն որոշել է «նորմալ» հեղուկի խտությունը, որը հավասար է 0-ի 0-ական ջերմաստիճանում և աճում է ջերմաստիճանի բարձրացման հետ։ Այսպես կոչված լամբդայի ջերմաստիճանում, որտեղ նորմալ բաղադրիչի խտությունը հավասար է ընդհանուր խտությանը, հելիում 4-ը կորցնում է իր գերհոսունությունը։

Գերհոսուն հելիում 4-ի ջերմունակության առանձնահատկությունները բացատրելու նպատակով Լանդաուն ենթադրել է որոշակի գրգռման գոյության մասին, որը նա անվանել է «Ռոտոն», բայց ճշգրիտ տվյալներն ստանալուց հետո նա որոշել է, որ ռոտոնը չի տարբերվում ձայնի բարձր ինպուլսային տարբերակից։

Լանդաուի տեսությունը մանրամասնորեն մշակել է հեղուկ հելիումի բաղադրիչների կառուցվածքը։ Գերհոսունության բաղադրիչների մանրադիտակային տեսության ստեղծման առաջին փորձը կատարել են Ֆրից Լոնդոնը և Տիշան։ Հետագայում տարբեր գիտնականներ առաջարկել են մանրադիտակային այլ մոդելներ։ Նրանց գլխավոր նպատակն է գերհոսուն վիճակում հելիումի ատոմների միջև մասնակի փոխազդեցությունն արտահայտել քվանտային մեխանիկայի սկզբունքներից ելնելով։ Մինչ օրս առաջարկվել են այդպիսի մի քանի մոդելներ՝ պտույտային օղակների մոդելները, պինդ ոլորտների մոդելները, գաուսսյան կլաստերային տեսությունները և այլն։

Պտույտի օղակի մոդելը

Լանդաուն ենթադրում էր, որ պտտողականությունը հելիում-4-ում առաջանում է պտտվող թերթիկների ձևով, բայց ապացուցվելլ է, որ նման թերթիկներն անկայուն են։ Օնզագերը և նրանից անկախ Ռիչարդ Ֆեյմանը ցույց են տվել, որ պտույտները հայտնվում են քվանտային պտտվող գծերի տեսքով։ Նրանք նաև զարգացրել են քվանտային պտտվող օղակների գաղափարը։ 1940-ական թվականներին Արիե Բայլը, իսկ 1955 թվականին՝ Ֆեյմանը ռոտոնների համար մշակել են մանրադիտակային տեսություններ, ինչը դիտարկվել է Պավլևսկու նեյտրոնների էլաստիկ ցրման փորձում։ Հետագայում Ֆեյմանը խոստովանել է, որ իր մոդելը փորձի հետ տալիս է միայն որակական համապատասխանություն։

Կոշտ ոլորտի մոդելներ

Կոշտ ոլորտի մոդելները օգտագործում են պարզեցված ձևով գերհոսուն հելիում-4-ի ատոմների փոխազդեցության դեպքում։ Մասնավորապես ներուժը ենթադրվում է կոշտ ոլորտների տեսքով։ Այս մոդելներում որակապես ձևավորվում է Լանդաուի գրգռման սպեկտորը։

Գաուսյան կլաստերային մոտեցում

Այս երկմասշտաբային մոտեցումը նկարագրում է հելիում-4-ի գերհոսուն բաղադրիչը։ Այն կազմված է երկու ներմուծված մոդելներից, որոնք փոխկապակցված են պարամետրային տարածությամբ։ Կարճալիք մասը բնութագրում է հոսքի փաթեթի ներքին կառուցվածքը՝ օգտագործելով ոչ յուրահատուկ մոտեցում՝ Շրեդինգի լոգարիթմական հավասարման միջոցով․

$i{\frac {\partial \psi }{\partial t}}+\Delta \psi +\psi \ln |\psi |^{2}=0$

Կոմպլեքս ֆունկցիայի համար $\psi =\psi (\mathrm {\mathbf {x} } ,t)$, որտեղ $\Delta \,$ լապլասիան է մինչև $\mathrm {\mathbf {x} }$ վեկտոր, այն ենթադրում է գաուսականի նման վարքագիծ, տարրի խտության և միջմասնիկային պոտենցիալի ներքին փոխազդեցություն։ Երկարալիք մասը այդպիսի տարրերի մարմինների քվանտային տեսությունն է, որը զբաղվում է դրանց դինամիկայով և փոխազդեցություններով։ Այսպիսի մոտեցումը ֆոնոնային, մաքսոնային և ռոտոնային գրգռականությունների միասնական նկարագրման հնարավորություն է տալիս, և նշանակալից համաձայնեցվածություն ունի իր փորձի հետ։ Օգտագործելով միայն մեկ կարևոր չափանիշ՝ կարելի մեծ ճշգրտությամբ արտածել Լանդաուի ռատոնային սպեկտրը, լույսի արագությունը և գերհոսուն հոլիումի-4-ի կառուցվածքային գործոնը։ Այս մոդելը օգտագործում է Բոզեի քվանտային հեղուկների ընդհանուր տեսությունը, որը հիմնված է դիսսիպատիվ տիպի էներգիայի ներմուծման վրա, ինչը կապված է Էվերետ-Գրիշմանի քվանտային ֆունկցիայի հետ։

Գործնական կիրառություններ

Վերջին ժամանակներում գերհոսուն հելիում-4-ը հաջողությամբ օգտագործվում է քիմիական սպեկտրոսկոպիկ մեթոդներում՝ որպես քվանտային լուծիչ։ Գերհոսուն հելիումում կաթիլային սպեկտրոսկոպիան մեծ հետաքրքրություն է ներկայացնում գազի մոլեկուլների հետազոտման համար, քանի որ գերհոսուն միջավայրը մոլեկուլներին ազատ պտտման հնարավորություն է տալիս, ինչի պատճառով մոլեկուլը իրեն դրսևորում է ինչպես «գազային» ֆազում։ Գերհոսուն հելիումի կաթիլներն ունեն բնորոշ մոտավորապես 0,4 Կ ջերմաստիճան, ինչը սառեցնում է հոսուն մոլեկուլը (կամ մոլեկուլները) մինչև ռովիբրիոն վիճակի (պտտվողների միջև միաժամանակյա փոխազդեցություն, տատանողական և էլեկտրոնային աստիճանների ազատություն մոլեկուլում)։

Գերհոսուն հոլիում-4-ում հելիում-3-ի լուծումը հանգեցնում է խառնուրդի սառեցմանը, ինչը հնարավորություն է տալիս հասնել ավելի ցածր ջերմաստիճանների։ Այս գործընթացն օգտագործվում է նոսրացված սառնարաններում։ Երբ լուծույթում հելիում-3-ի կոնցենտրացիան հասնում է հագեցվածության մակարդակի (մոտավորապես 7 %, կախված է ջերմաստիճանից), իսկ ջերմաստիճանը իջնում է մինչև 870 միլիկելվին (մԿ), լուծույթը ինքնաբերաբար բաժանվում է երկու ֆազի՝ գերհոսուն լուծույթ հելիում-3-ը հելիում-4-ում (պարունակում է մոտավորապես 6,6 % հելիում-3) և հելիում-4-ի լուծույթը հելիում-3-ում (գրեթե ամբողջությամբ կազմված է հելիում-3-ից)։ Հելիում-3-ով հարուստ ֆազը կարելի է առանձնացնել հելիում-3-ը գոլորշիացնելով (500—700 մԿ ջերմաստիճանում, դրա գոլորշու մասնակի ճնշումը ավելի մեծ է, քան հելիում-4-ինը), սառեցնել և նորից լցնել լուծման խցիկներ։ Այսպիսով լուծման խցիկում ջերմաստիճանը կրկին նվազում է։ Տեսականորեն այս գործընթացը կարելի է անվերջ շարունակել՝ ստանալով ավելի ու ավելի ցածր ջերմաստիճաններ։ Սակայն սարքավորման չափը աճում է հակադարձ համեմատականորեն T⁴ և 0,2մԿ-ից ցածր ջերմաստիճանում այն դառնում է չափազանց մեծ և թանկ։

Գերհոսուն հելիումով սառեցումը մեծ կիրառություն է գտել տիեզերանավերում, մասնավորապես, գերզգայուն գիրոսկոպերի սառեցման համար, որոնք հնարավորություն են տալիս չափել որոշ տեսականորեն կանխատեսված գրավիտացիոն էֆեկտներ։

• Gravity Probe տիեզերանավում կապարային և նիոբիումային գիրոսկոպները ընկղմվել են հեղուկ հելիումով թերմուսի մեջ 2 Կ ջերմաստիճանում, ինչը նրանց թույլ է տվել պահպանել գերհաղորդիչ վիճակը։

Ինչպես նաև էլեկտրամսգնիսական ճառագայթումը չափող բոլոմետրերի համար։

• IRAS ինֆրակարմիր աստղագիտական արբանյակը, որը գործարկվել է 1983 թվականի հունվարին, ինֆրակարմիր միջակայքում տվյալների հավաքման համարսառեցվել է 73կգ (720 լիտր) գերհոսուն հելիումի օգնությամբ՝ պահպանելով 1,6 Կ ջերմաստիճան (−271,55 °C)։
• Սառեցման նման համակարգ օգտագործվել է COBE արբանյակում, որն ուսումնասիրում էր ռելեկտիվ ճառագայթումը (գործարկվել է 1989 թվականի նոյեմբերին)։ Նրանում առկա էր 650 լիտր գերհոսուն հելիում։
• Պլանկ տիեզերական աստղադիտակում (2009-2013), որն աշխատում էր ցուցիչների մինչև 0,1 Կ ջերմաստիճան սառեցման ուղղությամբ, կիրառվել է լուծման ռեֆրեժատոր։
• Ջեյմս Կլերկ Մաքսվելի աստղադիտակի վրայի նմանատիպ ռեֆրեժատորը ունի բազային 50 մԿ ջերմաստիճան և պահպանում է բոլոմետրի մոտավորապես 75 մԿ ջերմաստիճան։

Գերհոսուն հելիումի տեխնոլոգիան օգտագործվում է ցածր ջերմաստիճանային սահմանները ընդլայնելու համար։ Մինչև հիմա սահմանը կազմում է 1,19 Կ, բայց հնարավոր է հասնել 0,7 Կ-ի։

Գրականություն

• London, F. Superfluids (Wiley, New York, 1950)
• D.R. Tilley and J. Tilley Superfluidity and Superconductivity. — Bristol: IOP Publishing Ltd., 1990.
• Хаген Кляйнерт, Gauge Fields in Condensed Matter, Vol. I, «SUPERFLOW AND VORTEX LINES», pp. 1–742, Paperback ISBN 9971-5-0210-0 (հասանելի է առցանց)
• Antony M. Guénault: Basic superfluids. Taylor & Francis, London 2003, ISBN 0-7484-0891-6
• James F. Annett: Superconductivity, superfluids, and condensates. Oxford Univ. Press, Oxford 2005, ISBN 978-0-19-850756-7
• Leggett, A. Superfluidity(անգլ.) // Reviews of Modern Physics : journal. — 1999. — Т. 71. — № 2. — С. S318—S323. —  —
• Philippe Lebrun & Laurent Tavian: The technology of superfluid helium
• Кресин В.З. Сверхпроводимость и сверхтекучесть. — 2, перераб.. — 1978. — С. 192.(ռուս.)

Արտաքին հղումներ

• Сверхтекучая плотность в непрерывных и дискретных пространствах: Избежание неправильных представлений
• Сверхтекучий Жидкий гелий II: демонстрации лямбда точки перехода/парадокс вязкости/Двухжидкостная модель/фонтанный эффект/ползучая плёнка/второй звук.
• Видео со странным поведением сверхтекучего гелия
• Сверхтекучие фазы гелия
• Superfluid Helium Droplets: An Ultracold Nanolaboratory
• http://web.mit.edu/newsoffice/2005/matter.html
• Индийская статья о сверхтекучих состояния Արխիվացված 2003-12-06 Wayback Machine