Բուլյան հանրահաշիվ
| Բուլյան հանրահաշիվ անգլ.՝ Boolean algebra | |
|---|---|
 | |
| Տեսակ | մաթեմատիկայի ճյուղ |
| Դաս | հանրահաշիվ |
| Անվանված է | Ջորջ Բուլ |
Այս հոդվածը հանրահաշվի ճյուղերից մեկի մասին է։
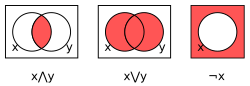
Բուլյան հանրահաշիվ, մաթեմատիկայում և մաթեմատիկական տրամաբանության մեջ հանրահաշվի մի ենթաճյուղ, որտեղ փոփոխականների արժեքները համարվում են «ճշմարիտ» կամ «սխալ» ասույթներ, և սովորաբար դրանք արտահայտվում են 1 ու 0 թվերով։ Ի տարբերություն տարրական հանրահաշվի, որտեղ փոփոխականների արժեքները հիմնականում թվեր են, և իրենց հիմնական գործողություններն են գումարումը և բազմապատկումը, Բուլյան հանրահաշվում հիմնական գործողություններ են համարվում կոնյունկցիան՝ «և» տրամաբանական շաղկապով, որը արտահայտվում է ∧ նշանով, դիզյունկցիան՝ «կամ» շաղկապի կիրառմամբ, որը արտահայտվում է ∨ նշանով և հերքումը, որը ժխտում է դատողությունը` ցույց տալով, որ հակառակն է ճիշտ և նշանակվում է ¬ նշանով։
Բուլյան հանրահաշիվը ներկայացվել է 1854 թվականին Ջորջ Բուլի կողմից իր «Մտքի կանոնների ուսումնասիրություն» գրքում[1]։ Ըստ Հանթինգթոնի՝ «Բուլյան հանրահաշիվ» տերմինն առաջին անգամ առաջարկվել է Շեֆֆերի կողմից 1913 թվականին[2], թեեւ Չարլզ Սանդերս Պերսը դեռևս 1880 թվականին իր «Պարզագույն մաթեմատիկա» գրքի առաջին գլուխը վերնագրել է «Մեկ հաստատունով Բուլյան հանրահաշիվ»[3]։
Բուլի առաջին գիրքը, որը հրապարակվել է 1847 թվականին և վերնագրված է «Տրամաբանության մաթեմատիկական վերլուծություն», իրենում ներառում էր իսկական, բնագիր տեսությունը։ Սա առաջարկված է եղել որպես մաթեմատիկական լեզու, որը զբաղվում էր տրամաբանության հարցերով, ինչը ներկայումս անհրաժեշտ է ժամանակակից թվային սարքավորումներ կառուցելու համար, ծրագրավորման լեզուներում ու սովորաբար կրճատված է որպես bool տեսակ ու բացի այդ այն գոյություն ունի որպես հիմնական տվյալ բոլոր ժամանակակից ծրագրավորման լեզուներում։ Բուլյան հանրահաշիվը հիմնային դեր ունի թվային էլեկտրոնիկայի զարգացման մեջ։ Այն նաև օգտագործվում է վիճակագրության և բազմությունների տեսության մեջ[4]։
Պատմություն[խմբագրել | խմբագրել կոդը]
Բուլյան հանրահաշիվն ավելի վաղ ժամանակներից գոյություն ունի, քան աբստրակտ հանրահաշիվը և մաթեմատիկական տրամաբանությունը, ինչևէ այն կապվում է այս երկու ոլորտների ծագման հետ[5]։ Բուլյան հանրահաշիվը կատարելագործվել է 19րդ դարի վերջին Ջևոնսի, Շրյոդերի, Հանթինգթոնի և ուրիշների կողմից։ Կատարելագործվում է այնքան մինչև, որ ստանում է ժամանակակից մաթեմատիկական կառուցվածքի տեսք։ Իրականում Մ.Հ. Սթոունը ապացուցել է, որ յուրաքանչյուր Բուլյան հանրահաշիվ իզոմորֆ է բազմությունների հանրահաշվին[6]։
Երբ 1930-ական թվականներին Քլոուդ Շենոնը ուսումնասիրում էր անջատիչներով կառավարվող էլեկտրական շղթաները, նա նկատեց նմաննություններ բուլյան հանրահաշվի գործողությունների հետ և հանրահաշվորեն նկարագրեց դրանց աշխատանքը տրամաբանական փականների միջոցով։
Արժեքներ[խմբագրել | խմբագրել կոդը]
Մինչդեռ տարրական հանրահաշվում արտահայտությունները մեծ մասամբ թվեր են ցույց տալիս, բուլյան հանրահաշվում դրանք ցույց են տալիս տրամաբանական արժեքը ՝ ճիշտ և սխալ։ Այս արժեքները ներկայացվածներ են բիթերով (կամ երկուական նիշերով), ավելի կոնկրետ՝ 0 և 1։ Դրանք ամբողջ թվեր՝ 0 և 1-ի նման չեն իրենց պահում, որոնց համար 1+1=2, այլ 2 տարրանոց վերջավոր դաշտ տարրերի պես, որոնց համար 1+1=0, որտեղ “+”-ը գործում է, որպես բուլյան հանրահածվի XOR այսպես կոչված «բացառող կամ»։
Բուլյան հանրահաշիվը բացի այդ գործ ունի նաև ֆունկցիաների հետ, որոնք սահմանված են {0,1} բազմության վրա։ Բիթերի հաջորդականությունն այդպիսի ֆունկցիա է, որը հաճախ է օգտագործվում։ Մեկ ուրիշ տարածված օրինակ է ինդիկատոր ֆունկցիան։
Ինչպես տարրական հանրահաշվում՝ Բուլյան հանրահաշվում ևս կարելի է զարգացնել հանրահաշվական նույնությունների վրա հիմնված տեսություն՝ անկախ փոփոխականների արժեքից։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Բուլ, Ջորջ (2003) [1854]. An Investigation of the Laws of Thought. Prometheus Books. ISBN 978-1-59102-089-9.
- ↑ E. V. Huntington. "New sets of independent postulates for the algebra of logic, with special reference to Whitehead and Russell's Principia mathematica", in Trans. Amer. Math. Soc. 35 (1933), 274-304; footnote, page 278.
- ↑ Peirce, Charles S. (1931). Collected Papers. Vol. 3. Harvard University Press. էջ 13. ISBN 978-0-674-13801-8.
- ↑ Givant, Steven; Halmos, Paul (2009). Introduction to Boolean Algebras. Undergraduate Texts in Mathematics, Springer. ISBN 978-0-387-40293-2.
- ↑ J. Michael Dunn; Gary M. Hardegree (2001). Algebraic methods in philosophical logic. Oxford University Press US. էջ 2. ISBN 978-0-19-853192-0.
- ↑ Marshall H. Stone (1936) "The Theory of Representations of Boolean Algebras," Transactions of the American Mathematical Society 40: 37-111.
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 2, էջ 602)։ |
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Բուլյան հանրահաշիվ» հոդվածին։ |
| ||||||||||||
| ||||||||||
