Հակադարձ եռանկյունաչափական ֆունկցիաներ (շրջանային ֆունկցիաներ , արկֆունկցիաներ ), մաթեմատիկական ֆունկցիաներ , որոնք համարվում են եռանկյունաչափական ֆունկցիաների հակադարձը։ Հակադարձ եռանկյունաչափական ֆունկցիաները հիմնականում լինում են վեց տեսակի.
արկսինուս (նշանակում
:
a
r
c
s
i
n
x
;
a
r
c
s
i
n
x
{\displaystyle :\mathrm {arcsin} \,x;\mathrm {arcsin} \,x}
x
{\displaystyle x}
արկկոսինուս (նշանակում։
a
r
c
c
o
s
x
;
a
r
c
c
o
s
x
{\displaystyle \mathrm {arccos} \,x;\mathrm {arccos} \,x}
x
{\displaystyle x}
արկտանգենս (նշանակում։
a
r
c
t
g
x
{\displaystyle \mathrm {arctg} \,x}
a
r
c
t
a
n
x
{\displaystyle \mathrm {arctan} \,x}
արկկոտանգենս (նշանակում։
a
r
c
c
t
g
x
{\displaystyle \mathrm {arcctg} \,x}
a
r
c
c
o
t
x
{\displaystyle \mathrm {arccot} \,x}
a
r
c
c
o
t
a
n
x
{\displaystyle \mathrm {arccotan} \,x}
արկսեկանս (նշանակում։
a
r
c
s
e
c
x
{\displaystyle \mathrm {arcsec} \,x}
արկկոսեկանս (նշանակում։
a
r
c
c
o
s
e
c
x
{\displaystyle \mathrm {arccosec} \,x}
a
r
c
c
s
c
x
{\displaystyle \mathrm {arccsc} \,x}
Հակադարձ եռանկյունաչափական ֆունկցիաների անունները ստեղծվել են համապատասխան եռանկյունաչափական ֆունկցիաներին «արկ-» նախածանցը ավելացնելով (լատին․ ՝ arc usեռանկյունաչափական ֆունկցիաների երկրաչափական արժեքները կապված են միավոր շրջանագծի վրա այդ աղեղի երկարությունից (կամ անկյունից)։ Սովորական սինուսը հնարավորություն է տալիս աղեղից գտնել նրան ձգող լարը, իսկ հակադարձ ֆունկցիան որոշում է հակառակ խնդիրը։ Եռակնյունաչափական ֆունկցիաների հակադարձ եղանակի մասին հայտնել է ավստրիացի մաթեմատիկոս Կարլ Շերֆերը (գերմ. ՝ Karl Scherffer ; 1716-1783), բայց դրա արմատները հիմնակում պատկանում էին Լագրանժին ։ Եռանկյունաչափական ֆունկցիաների համար առաջին հատուկ նշանը ստեղծել է Դանիել Բերնուլին ՝ 1729 թվականին։ Անգլիական և գերմանական շատ դպրոցների մինչև 19-րդ դարի վերջը առաջարկում էին այլ նշանակումներ.
sin
−
1
,
1
sin
{\displaystyle \sin ^{-1},{\frac {1}{\sin }}}
[1] −1 , cos−1 եղանակը[2]
Եռանկյունաչափական ֆունկցիաների հակադարձները երկիմաստ էին։ Այսինքն արկֆունկցիաների արժեքները իրենցից ներկայացնում էին բազմաթիվ անկյուններ (աղեղի), որի պատճառով համապատասխան ուղիղ եռանկյունաչափական ֆունկցիայի համար ճիշտ էր տվյալ արժեքը։ Օրինակ,
arcsin
1
/
2
{\displaystyle \arcsin 1/2}
(
π
6
,
5
π
6
,
13
π
6
,
17
π
6
…
(
30
∘
,
150
∘
,
390
∘
,
510
∘
…
)
)
{\displaystyle \left({\frac {\pi }{6}},{\frac {5\pi }{6}},{\frac {13\pi }{6}},{\frac {17\pi }{6}}\dots ~(30^{\circ },150^{\circ },390^{\circ },510^{\circ }\dots )\right)}
1
/
2
{\displaystyle 1/2}
−
1
⩽
α
⩽
1
{\displaystyle -1\leqslant \alpha \leqslant 1}
sin
x
=
α
{\displaystyle \sin x=\alpha }
x
=
(
−
1
)
n
arcsin
α
+
π
n
,
n
=
0
,
±
1
,
±
2
,
…
.
{\displaystyle x=(-1)^{n}\arcsin \alpha +\pi n,~n=0,\pm 1,\pm 2,\dots ~.}
[3]
arcsin
x
+
arccos
x
=
π
2
{\displaystyle \arcsin x+\arccos x={\frac {\pi }{2}}}
arctg
x
+
arcctg
x
=
π
2
{\displaystyle \operatorname {arctg} \,x+\operatorname {arcctg} \,x={\frac {\pi }{2}}}
Անուն
Նշանակում
Սահմանում
Միջակայք
Անվանական արժքի միջակայք
Անվանական արժեքի միջակայք
arcsine y = arcsin x x = sin y −1 ≤ x ≤ 1
−π/2 ≤ y ≤ π/2
−90° ≤ y ≤ 90°
arccosine y = arccos x x = cos y −1 ≤ x ≤ 1
0 ≤ y ≤ π
0° ≤ y ≤ 180°
arctangent y = arctan x x = tg y բոլոր իրական թվերը
−π/2 < y < π/2
−90° < y < 90°
arccotangent y = arccot x x = ctg y բոլոր իրական թվերը
0 < y < π
0° < y < 180°
arcsecant y = arcsec x x = sec y x ≤ −1 or 1 ≤ x 0 ≤ y < π/2 or π/2 < y ≤ π
0° ≤ y < 90° or 90° < y ≤ 180°
arccosecant y = arccsc x x = csc y x ≤ −1 or 1 ≤ x −π/2 ≤ y < 0 or 0 < y ≤ π/2
-90° ≤ y < 0° or 0° < y ≤ 90°
Կապը եռանկյունաչափական և հակադարձ եռանկյունաչափական ֆունկցիաների միջև [ խմբագրել | խմբագրել կոդը ] Եռանկյունաչափական և հակադարձ եռանկյունաչափական ֆունկցիաները աղյուսակավորված են ներքևում.
θ
{\displaystyle \theta }
sin
θ
{\displaystyle \sin \theta }
cos
θ
{\displaystyle \cos \theta }
tan
θ
{\displaystyle \tan \theta }
Գծագիր
arcsin
x
{\displaystyle \arcsin x}
sin
(
arcsin
x
)
=
x
{\displaystyle \sin(\arcsin x)=x}
cos
(
arcsin
x
)
=
1
−
x
2
{\displaystyle \cos(\arcsin x)={\sqrt {1-x^{2}}}}
tan
(
arcsin
x
)
=
x
1
−
x
2
{\displaystyle \tan(\arcsin x)={\frac {x}{\sqrt {1-x^{2}}}}}
arccos
x
{\displaystyle \arccos x}
sin
(
arccos
x
)
=
1
−
x
2
{\displaystyle \sin(\arccos x)={\sqrt {1-x^{2}}}}
cos
(
arccos
x
)
=
x
{\displaystyle \cos(\arccos x)=x}
tan
(
arccos
x
)
=
1
−
x
2
x
{\displaystyle \tan(\arccos x)={\frac {\sqrt {1-x^{2}}}{x}}}
arctan
x
{\displaystyle \arctan x}
sin
(
arctan
x
)
=
x
1
+
x
2
{\displaystyle \sin(\arctan x)={\frac {x}{\sqrt {1+x^{2}}}}}
cos
(
arctan
x
)
=
1
1
+
x
2
{\displaystyle \cos(\arctan x)={\frac {1}{\sqrt {1+x^{2}}}}}
tan
(
arctan
x
)
=
x
{\displaystyle \tan(\arctan x)=x}
arccot
x
{\displaystyle \operatorname {arccot} x}
sin
(
arccot
x
)
=
1
1
+
x
2
{\displaystyle \sin(\operatorname {arccot} x)={\frac {1}{\sqrt {1+x^{2}}}}}
cos
(
arccot
x
)
=
x
1
+
x
2
{\displaystyle \cos(\operatorname {arccot} x)={\frac {x}{\sqrt {1+x^{2}}}}}
tan
(
arccot
x
)
=
1
x
{\displaystyle \tan(\operatorname {arccot} x)={\frac {1}{x}}}
arcsec
x
{\displaystyle \operatorname {arcsec} x}
sin
(
arcsec
x
)
=
x
2
−
1
x
{\displaystyle \sin(\operatorname {arcsec} x)={\frac {\sqrt {x^{2}-1}}{x}}}
cos
(
arcsec
x
)
=
1
x
{\displaystyle \cos(\operatorname {arcsec} x)={\frac {1}{x}}}
tan
(
arcsec
x
)
=
x
2
−
1
{\displaystyle \tan(\operatorname {arcsec} x)={\sqrt {x^{2}-1}}}
arccsc
x
{\displaystyle \operatorname {arccsc} x}
sin
(
arccsc
x
)
=
1
x
{\displaystyle \sin(\operatorname {arccsc} x)={\frac {1}{x}}}
cos
(
arccsc
x
)
=
x
2
−
1
x
{\displaystyle \cos(\operatorname {arccsc} x)={\frac {\sqrt {x^{2}-1}}{x}}}
tan
(
arccsc
x
)
=
1
x
2
−
1
{\displaystyle \tan(\operatorname {arccsc} x)={\frac {1}{\sqrt {x^{2}-1}}}}
Կապը հակադարձ եռանկյունաչափական ֆունկցիաների միջև [ խմբագրել | խմբագրել կոդը ] arcsin(x ) (կարմիր) և arccos(x ) (կապույտ) ֆունկցիաների գրաֆիկների փոխադարձ դասավորությունը: arctan(x ) և arccot(x ) ֆունկցիաների գրաֆիկների փոխադարձ դասավորությունը: arcsec(x ) և arccsc(x ) ֆունկցիաների գրաֆիկների փոխադարձ դասավորությունը: Լրացուցիչ անկյուններ.
arccos
x
=
π
2
−
arcsin
x
arccot
x
=
π
2
−
arctan
x
arccsc
x
=
π
2
−
arcsec
x
{\displaystyle {\begin{aligned}\arccos x&={\frac {\pi }{2}}-\arcsin x\\[0.5em]\operatorname {arccot} x&={\frac {\pi }{2}}-\arctan x\\[0.5em]\operatorname {arccsc} x&={\frac {\pi }{2}}-\operatorname {arcsec} x\end{aligned}}}
Բացասական արգումենտներ.
arcsin
(
−
x
)
=
−
arcsin
x
arccos
(
−
x
)
=
π
−
arccos
x
arctan
(
−
x
)
=
−
arctan
x
arccot
(
−
x
)
=
π
−
arccot
x
arcsec
(
−
x
)
=
π
−
arcsec
x
arccsc
(
−
x
)
=
−
arccsc
x
{\displaystyle {\begin{aligned}\arcsin(-x)&=-\arcsin x\\\arccos(-x)&=\pi -\arccos x\\\arctan(-x)&=-\arctan x\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccot} x\\\operatorname {arcsec}(-x)&=\pi -\operatorname {arcsec} x\\\operatorname {arccsc}(-x)&=-\operatorname {arccsc} x\end{aligned}}}
Դրական արգումենտներ.
arccos
(
1
/
x
)
=
arcsec
x
arcsin
(
1
/
x
)
=
arccsc
x
arctan
(
1
/
x
)
=
π
2
−
arctan
x
=
arccot
x
,
if
x
>
0
arctan
(
1
/
x
)
=
−
π
2
−
arctan
x
=
arccot
x
−
π
,
if
x
<
0
arccot
(
1
/
x
)
=
π
2
−
arccot
x
=
arctan
x
,
if
x
>
0
arccot
(
1
/
x
)
=
3
π
2
−
arccot
x
=
π
+
arctan
x
,
if
x
<
0
arcsec
(
1
/
x
)
=
arccos
x
arccsc
(
1
/
x
)
=
arcsin
x
{\displaystyle {\begin{aligned}\arccos(1/x)&=\operatorname {arcsec} x\\[0.3em]\arcsin(1/x)&=\operatorname {arccsc} x\\[0.3em]\arctan(1/x)&={\frac {\pi }{2}}-\arctan x=\operatorname {arccot} x\,,{\text{if}}x>0\\[0.3em]\arctan(1/x)&=-{\frac {\pi }{2}}-\arctan x=\operatorname {arccot} x-\pi \,,{\text{ if}}x<0\\[0.3em]\operatorname {arccot}(1/x)&={\frac {\pi }{2}}-\operatorname {arccot} x=\arctan x\,,{\text{ if}}x>0\\[0.3em]\operatorname {arccot}(1/x)&={\frac {3\pi }{2}}-\operatorname {arccot} x=\pi +\arctan x\,,{\text{ if}}x<0\\[0.3em]\operatorname {arcsec}(1/x)&=\arccos x\\[0.3em]\operatorname {arccsc}(1/x)&=\arcsin x\end{aligned}}}
arccos
x
=
arcsin
1
−
x
2
,
if
0
≤
x
≤
1
arctan
x
=
arcsin
x
x
2
+
1
{\displaystyle {\begin{aligned}\arccos x&=\arcsin {\sqrt {1-x^{2}}}\,,{\text{ if}}0\leq x\leq 1\\\arctan x&=\arcsin {\frac {x}{\sqrt {x^{2}+1}}}\end{aligned}}}
arcsin
x
=
2
arctan
x
1
+
1
−
x
2
arccos
x
=
2
arctan
1
−
x
2
1
+
x
,
if
−
1
<
x
≤
+
1
arctan
x
=
2
arctan
x
1
+
1
+
x
2
{\displaystyle {\begin{aligned}\arcsin x&=2\arctan {\frac {x}{1+{\sqrt {1-x^{2}}}}}\\[0.5em]\arccos x&=2\arctan {\frac {\sqrt {1-x^{2}}}{1+x}}\,,{\text{ if}}-1<x\leq +1\\[0.5em]\arctan x&=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}\end{aligned}}}
arctan
u
+
arctan
v
=
arctan
(
u
+
v
1
−
u
v
)
(
mod
π
)
,
u
v
≠
1
{\displaystyle \arctan u+\arctan v=\arctan \left({\frac {u+v}{1-uv}}\right){\pmod {\pi }}\,,\quad uv\neq 1\,}
Ստացվածը տանգենսների գումարման բանաձևն է.
tan
(
α
+
β
)
=
tan
α
+
tan
β
1
−
tan
α
tan
β
,
{\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}\,,}
α
=
arctan
u
,
β
=
arctan
v
:
{\displaystyle \alpha =\arctan u\,,\quad \beta =\arctan v\,:}
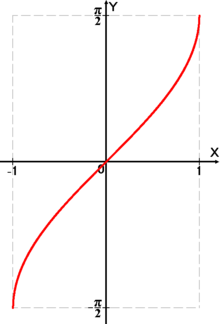
y
=
arcsin
x
{\displaystyle y=\arcsin x}
Արկսինուս m թվից կոչվում է այն x անկյունը՝ արտահայտված ռադիաններով , որի համար
sin
x
=
m
,
−
π
2
⩽
x
⩽
π
2
,
|
m
|
⩽
1
:
{\displaystyle \sin x=m,\,-{\frac {\pi }{2}}\leqslant x\leqslant {\frac {\pi }{2}},\,|m|\leqslant 1:}
y
=
sin
x
{\displaystyle y=\sin x}
y
=
arcsin
x
{\displaystyle y=\arcsin x}
sin
(
arcsin
x
)
=
x
{\displaystyle \sin(\arcsin x)=x\qquad }
−
1
⩽
x
⩽
1
{\displaystyle -1\leqslant x\leqslant 1}
arcsin
(
sin
y
)
=
y
{\displaystyle \arcsin(\sin y)=y\qquad }
−
π
2
⩽
y
⩽
π
2
{\displaystyle -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}}}
D
(
arcsin
x
)
=
[
−
1
;
1
]
{\displaystyle D(\arcsin x)=[-1;1]\qquad }
E
(
arcsin
x
)
=
[
−
π
2
;
π
2
]
{\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad }
arcsin
(
−
x
)
=
−
arcsin
x
{\displaystyle \arcsin(-x)=-\arcsin x\qquad }
arcsin
x
>
0
{\displaystyle \arcsin x>0\,}
0
<
x
⩽
1
{\displaystyle 0<x\leqslant 1}
arcsin
x
=
0
{\displaystyle \arcsin x=0\,}
x
=
0.
{\displaystyle x=0.}
arcsin
x
<
0
{\displaystyle \arcsin x<0\,}
−
1
⩽
x
<
0.
{\displaystyle -1\leqslant x<0.}
arcsin
x
=
{
arccos
1
−
x
2
,
0
⩽
x
⩽
1
−
arccos
1
−
x
2
,
−
1
⩽
x
<
0
{\displaystyle \arcsin x=\left\{{\begin{matrix}\arccos {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\-\arccos {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.}
arcsin
x
=
arctg
x
1
−
x
2
{\displaystyle \arcsin x=\operatorname {arctg} {\frac {x}{\sqrt {1-x^{2}}}}}
arcsin
x
=
{
arcctg
1
−
x
2
x
,
0
<
x
⩽
1
arcctg
1
−
x
2
x
−
π
,
−
1
⩽
x
<
0
{\displaystyle \arcsin x=\left\{{\begin{matrix}\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}}-\pi ,\qquad -1\leqslant x<0\end{matrix}}\right.}
Տրված է
y
=
sin
x
{\displaystyle y=\sin x}
մոնոտոն , բայց դրա հակադարձ
y
=
arcsin
x
{\displaystyle y=\arcsin x}
[
−
π
2
;
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}
y
=
sin
x
{\displaystyle y=\sin x}
[
−
π
2
;
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}
y
=
arcsin
x
{\displaystyle y=\arcsin x}
y
=
sin
x
{\displaystyle y=\sin x}
[
−
π
2
;
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}
O
x
y
{\displaystyle Oxy}
կիսորդը )
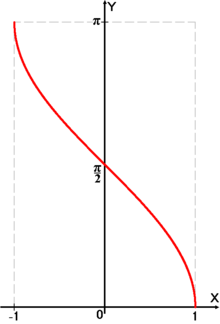
y
=
arccos
x
{\displaystyle y=\arccos x}
Արկոսինուս m թվից կոչվում է այն x անկյունը՝ արտահայտված ռադիաններով, որի համար
cos
x
=
m
,
0
⩽
x
⩽
π
,
|
m
|
⩽
1
:
{\displaystyle \cos x=m,\qquad 0\leqslant x\leqslant \pi ,|m|\leqslant 1:}
y
=
cos
x
{\displaystyle y=\cos x}
y
=
arccos
x
{\displaystyle y=\arccos x}
cos
(
arccos
x
)
=
x
{\displaystyle \cos(\arccos x)=x}
−
1
⩽
x
⩽
1
,
{\displaystyle -1\leqslant x\leqslant 1,}
arccos
(
cos
y
)
=
y
{\displaystyle \arccos(\cos y)=y}
0
⩽
y
⩽
π
.
{\displaystyle 0\leqslant y\leqslant \pi .}
D
(
arccos
x
)
=
[
−
1
;
1
]
,
{\displaystyle D(\arccos x)=[-1;1],}
E
(
arccos
x
)
=
[
0
;
π
]
.
{\displaystyle E(\arccos x)=[0;\pi ].}
arccos
(
−
x
)
=
π
−
arccos
x
{\displaystyle \arccos(-x)=\pi -\arccos x\,}
կոորդինատային հարթության
(
0
;
π
2
)
{\displaystyle \left(0;{\frac {\pi }{2}}\right)}
arccos
x
>
0
{\displaystyle \arccos x>0\,}
−
1
⩽
x
<
1.
{\displaystyle -1\leqslant x<1.}
arccos
x
=
0
{\displaystyle \arccos x=0\,}
x
=
1.
{\displaystyle x=1.\,}
arccos
x
=
π
2
−
arcsin
x
.
{\displaystyle \arccos x={\frac {\pi }{2}}-\arcsin x.}
arccos
x
=
{
arcsin
1
−
x
2
,
0
⩽
x
⩽
1
π
−
arcsin
1
−
x
2
,
−
1
⩽
x
<
0
{\displaystyle \arccos x=\left\{{\begin{matrix}\arcsin {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\\pi -\arcsin {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.}
arccos
x
=
{
arctg
1
−
x
2
x
,
0
<
x
⩽
1
π
+
arctg
1
−
x
2
x
,
−
1
⩽
x
<
0
{\displaystyle \arccos x=\left\{{\begin{matrix}\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\pi +\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad -1\leqslant x<0\end{matrix}}\right.}
arccos
x
=
2
arcsin
1
−
x
2
{\displaystyle \arccos x=2\arcsin {\sqrt {\frac {1-x}{2}}}}
arccos
x
=
2
arccos
1
+
x
2
{\displaystyle \arccos x=2\arccos {\sqrt {\frac {1+x}{2}}}}
arccos
x
=
2
arctg
1
−
x
1
+
x
{\displaystyle \arccos x=2\operatorname {arctg} {\sqrt {\frac {1-x}{1+x}}}}
Տրված է
y
=
cos
x
{\displaystyle y=\cos x}
y
=
arccos
x
{\displaystyle y=\arccos x}
[
0
;
π
]
{\displaystyle [0;\pi ]}
y
=
cos
x
{\displaystyle y=\cos x}
[
0
;
π
]
{\displaystyle [0;\pi ]}
y
=
arccos
x
{\displaystyle y=\arccos x}
y
=
x
{\displaystyle y=x}
y
=
cos
x
{\displaystyle y=\cos x}
[
0
;
π
]
{\displaystyle [0;\pi ]}
y
=
arctg
x
{\displaystyle y=\operatorname {arctg} \,x}
Արկտանգենս m թվից կոչվում է այն
α
{\displaystyle \alpha }
tg
α
=
m
,
−
π
2
<
α
<
π
2
:
{\displaystyle \operatorname {tg} \,\alpha =m,\qquad -{\frac {\pi }{2}}<\alpha <{\frac {\pi }{2}}:}
y
=
arctg
x
{\displaystyle y=\operatorname {arctg} x}
y
=
arctg
x
{\displaystyle y=\operatorname {arctg} x}
tg
(
arctg
x
)
=
x
{\displaystyle \operatorname {tg} \,(\operatorname {arctg} \,x)=x}
x
∈
R
,
{\displaystyle x\in \mathbb {R} ,}
arctg
(
tg
y
)
=
y
{\displaystyle \operatorname {arctg} \,(\operatorname {tg} \,y)=y}
−
π
2
<
y
<
π
2
,
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}},}
D
(
arctg
x
)
=
(
−
∞
;
∞
)
,
{\displaystyle D(\operatorname {arctg} \,x)=(-\infty ;\infty ),}
E
(
arctg
x
)
=
(
−
π
2
;
π
2
)
{\displaystyle E(\operatorname {arctg} \,x)=\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}
arctg
(
−
x
)
=
−
arctg
x
{\displaystyle \operatorname {arctg} (-x)=-\operatorname {arctg} x\qquad }
arctg
x
=
arcsin
x
1
+
x
2
{\displaystyle \operatorname {arctg} x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}}
arctg
x
=
arccos
1
1
+
x
2
{\displaystyle \operatorname {arctg} x=\arccos {\frac {1}{\sqrt {1+x^{2}}}}}
arctg
x
=
arcctg
1
x
{\displaystyle \operatorname {arctg} x=\operatorname {arcctg} {\frac {1}{x}}}
Տրված է
y
=
tg
x
{\displaystyle y=\operatorname {tg} \,x}
y
=
arctg
x
{\displaystyle y=\operatorname {arctg} \ x}
(
−
π
2
;
π
2
)
:
{\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right):}
y
=
tg
x
{\displaystyle y=\operatorname {tg} \ x}
(
−
π
2
;
π
2
)
{\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}
y
=
arctg
x
{\displaystyle y=\operatorname {arctg} \ x}
y
=
tg
x
{\displaystyle y=\operatorname {tg} \,x}
y
=
x
{\displaystyle y=x}
(
−
π
2
;
π
2
)
{\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}
y
=
arcctg
x
{\displaystyle y=\operatorname {arcctg} x}
Արկկոտանգենս m թվից կոչվում է այն x անկյունը՝ արտահայտված ռադիաններով, որի համար
ctg
x
=
m
,
0
<
x
<
π
:
{\displaystyle \operatorname {ctg} \,x=m,\qquad 0<x<\pi :}
y
=
arcctg
x
{\displaystyle y=\operatorname {arcctg} \,x}
y
=
arcctg
x
{\displaystyle y=\operatorname {arcctg} \,x}
նվազող ։
ctg
(
arcctg
x
)
=
x
{\displaystyle \operatorname {ctg} \,(\operatorname {arcctg} \,x)=x}
x
∈
R
,
{\displaystyle x\in \mathbb {R} ,}
arcctg
(
ctg
y
)
=
y
{\displaystyle \operatorname {arcctg} \,(\operatorname {ctg} \,y)=y}
0
<
y
<
π
,
{\displaystyle 0<y<\pi ,}
D
(
arcctg
x
)
=
(
−
∞
;
∞
)
,
{\displaystyle D(\operatorname {arcctg} \,x)=(-\infty ;\infty ),}
E
(
arcctg
x
)
=
(
0
;
π
)
:
{\displaystyle E(\operatorname {arcctg} \,x)=(0;\pi ):}
arcctg
(
−
x
)
=
π
−
arcctg
x
{\displaystyle \operatorname {arcctg} \,(-x)=\pi -\operatorname {arcctg} \,x}
(
0
;
π
2
)
{\displaystyle \left(0;{\frac {\pi }{2}}\right)}
arcctg
x
>
0
{\displaystyle \operatorname {arcctg} \,x>0}
x
{\displaystyle x}
arcctg
x
=
{
arcsin
1
1
+
x
2
,
x
⩾
0
π
−
arcsin
1
1
+
x
2
,
x
<
0
{\displaystyle \operatorname {arcctg} \,x=\left\{{\begin{matrix}\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\\pi -\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x<0\end{matrix}}\right.}
arcctg
x
=
π
/
2
−
arctg
x
:
{\displaystyle \operatorname {arcctg} x=\pi /2-\operatorname {arctg} x:}
Տրված է
y
=
ctg
x
{\displaystyle y=\operatorname {ctg} \,x}
y
=
arcctg
x
{\displaystyle y=\operatorname {arcctg} \,x}
(
0
;
π
)
{\displaystyle (0;\pi )}
y
=
ctg
x
{\displaystyle y=\operatorname {ctg} \,x}
(
0
;
π
)
{\displaystyle (0;\pi )}
y
=
arcctg
x
{\displaystyle y=\operatorname {arcctg} \,x}
y
=
x
{\displaystyle y=x}
y
=
ctg
x
{\displaystyle y=\operatorname {ctg} \,x}
(
0
;
π
)
{\displaystyle (0;\pi )}
Արկկոտանգենս ֆունկցիայի գրաֆիկը ստացվում է արկտանգենս ֆունկցիայի միջոցով, վերջինս օրդինատների առանցքով արտապատկերելով (որը պետք է փոխարինել արգումենտի նշանով.
x
→
−
x
{\displaystyle x\rightarrow -x}
π/2 միավորով. դա կարող ենք տերկայացնել հետևյալ բանաձևով՝
arcctg
x
=
arctg
(
−
x
)
+
π
/
2
:
{\displaystyle \operatorname {arcctg} x=\operatorname {arctg} (-x)+\pi /2:}
arcsec
(
x
)
=
arccos
(
1
x
)
{\displaystyle \mathop {\operatorname {arcsec} } \,(x)\,=\operatorname {arccos} \left({\frac {1}{x}}\right)\,}
arccosec
(
y
)
=
arcsin
(
1
y
)
{\displaystyle \mathop {\operatorname {arccosec} } \,(y)\,=\operatorname {arcsin} \left({\frac {1}{y}}\right)\,}
Հակադարձ եռանկյունաչափական ֆունկցիաների ածանցյալ [ խմբագրել | խմբագրել կոդը ]
(
arcsin
x
)
′
=
1
1
−
x
2
{\displaystyle (\arcsin x)'={\frac {1}{\sqrt {1-x^{2}}}}}
(
arccos
x
)
′
=
−
1
1
−
x
2
{\displaystyle (\arccos x)'=-{\frac {1}{\sqrt {1-x^{2}}}}}
(
arctg
x
)
′
=
1
1
+
x
2
{\displaystyle (\operatorname {arctg} \,x)'={\frac {1}{\ 1+x^{2}}}}
(
arcctg
x
)
′
=
−
1
1
+
x
2
{\displaystyle (\operatorname {arcctg} \,x)'=-{\frac {1}{\ 1+x^{2}}}}
Հակադարձ եռանկյունաչափական ֆունկցիաների ինտեգրալ [ խմբագրել | խմբագրել կոդը ] Իրական և կոմպլեքս x -երի համար.
∫
arcsin
x
d
x
=
x
arcsin
x
+
1
−
x
2
+
C
,
∫
arccos
x
d
x
=
x
arccos
x
−
1
−
x
2
+
C
,
∫
arctg
x
d
x
=
x
arctg
x
−
1
2
ln
(
1
+
x
2
)
+
C
,
∫
arcctg
x
d
x
=
x
arcctg
x
+
1
2
ln
(
1
+
x
2
)
+
C
,
∫
arcsec
x
d
x
=
x
arcsec
x
−
ln
(
x
(
1
+
x
2
−
1
x
2
)
)
+
C
,
∫
arccosec
x
d
x
=
x
arccosec
x
+
ln
(
x
(
1
+
x
2
−
1
x
2
)
)
+
C
:
{\displaystyle {\begin{aligned}\int \arcsin x\,dx&{}=x\,\arcsin x+{\sqrt {1-x^{2}}}+C,\\\int \arccos x\,dx&{}=x\,\arccos x-{\sqrt {1-x^{2}}}+C,\\\int \operatorname {arctg} \,x\,dx&{}=x\,\operatorname {arctg} \,x-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcctg} \,x\,dx&{}=x\,\operatorname {arcctg} \,x+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\,\right)\!\right)+C,\\\int \operatorname {arccosec} \,x\,dx&{}=x\,\operatorname {arccosec} \,x+\ln \left(x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\,\right)\!\right)+C:\end{aligned}}}
Իրական թվերի համար՝ x ≥ 1:
∫
arcsec
x
d
x
=
x
arcsec
x
−
ln
(
x
+
x
2
−
1
)
+
C
,
∫
arccosec
x
d
x
=
x
arccosec
x
+
ln
(
x
+
x
2
−
1
)
+
C
:
{\displaystyle {\begin{aligned}\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C,\\\int \operatorname {arccosec} \,x\,dx&{}=x\,\operatorname {arccosec} \,x+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C:\end{aligned}}}
ABC ուղղանկյուն եռանկյուն Հակադարձ եռանկյունաչափական ֆունկցիաները օգտագործում են եռանկյան անկյունները գտնելու համար, եթե հայտնի են նրա կողմները, օրինակ կոսինուսների թեորեմի միջոցով։
Ուղղանկյուն եռանկյան մեջ այդ ֆունկցիաները միանգամից տալիս են անկյունը.
α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
arcsin
z
=
−
i
ln
(
i
z
+
1
−
z
2
)
,
{\displaystyle {\begin{aligned}\arcsin z&{}=-i\ln(iz+{\sqrt {1-z^{2}}}),\end{aligned}}}
arccos
z
=
π
2
+
i
ln
(
i
z
+
1
−
z
2
)
,
{\displaystyle {\begin{aligned}\arccos z&{}={\dfrac {\pi }{2}}+i\ln(iz+{\sqrt {1-z^{2}}}),\end{aligned}}}
arctg
z
=
i
2
(
ln
(
1
−
i
z
)
−
ln
(
1
+
i
z
)
)
,
{\displaystyle {\begin{aligned}\operatorname {arctg} \,z&{}={\dfrac {i}{2}}(\ln(1-iz)-\ln(1+iz)),\end{aligned}}}
arcctg
z
=
i
2
(
ln
(
z
−
i
z
)
−
ln
(
z
+
i
z
)
)
,
{\displaystyle {\begin{aligned}\operatorname {arcctg} \,z&{}={\dfrac {i}{2}}\left(\ln \left({\dfrac {z-i}{z}}\right)-\ln \left({\dfrac {z+i}{z}}\right)\right),\end{aligned}}}
arcsec
z
=
arccos
(
z
−
1
)
=
π
2
+
i
ln
(
1
−
1
z
2
+
i
z
)
,
{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left(z^{-1}\right)={\dfrac {\pi }{2}}+i\ln \left({\sqrt {1-{\dfrac {1}{z^{2}}}}}+{\dfrac {i}{z}}\right),\end{aligned}}}
arccosec
z
=
arcsin
(
z
−
1
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
.
{\displaystyle {\begin{aligned}\operatorname {arccosec} \,z&{}=\arcsin \left(z^{-1}\right)=-i\ln \left({\sqrt {1-{\dfrac {1}{z^{2}}}}}+{\dfrac {i}{z}}\right).\end{aligned}}}





























































![{\displaystyle {\begin{aligned}\arccos x&={\frac {\pi }{2}}-\arcsin x\\[0.5em]\operatorname {arccot} x&={\frac {\pi }{2}}-\arctan x\\[0.5em]\operatorname {arccsc} x&={\frac {\pi }{2}}-\operatorname {arcsec} x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38e12876da2ea4b62a660e43e93d9ae73194388e)

![{\displaystyle {\begin{aligned}\arccos(1/x)&=\operatorname {arcsec} x\\[0.3em]\arcsin(1/x)&=\operatorname {arccsc} x\\[0.3em]\arctan(1/x)&={\frac {\pi }{2}}-\arctan x=\operatorname {arccot} x\,,{\text{if}}x>0\\[0.3em]\arctan(1/x)&=-{\frac {\pi }{2}}-\arctan x=\operatorname {arccot} x-\pi \,,{\text{ if}}x<0\\[0.3em]\operatorname {arccot}(1/x)&={\frac {\pi }{2}}-\operatorname {arccot} x=\arctan x\,,{\text{ if}}x>0\\[0.3em]\operatorname {arccot}(1/x)&={\frac {3\pi }{2}}-\operatorname {arccot} x=\pi +\arctan x\,,{\text{ if}}x<0\\[0.3em]\operatorname {arcsec}(1/x)&=\arccos x\\[0.3em]\operatorname {arccsc}(1/x)&=\arcsin x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d83d08dae0e31939e0cd147314efc326e0c774f8)

![{\displaystyle {\begin{aligned}\arcsin x&=2\arctan {\frac {x}{1+{\sqrt {1-x^{2}}}}}\\[0.5em]\arccos x&=2\arctan {\frac {\sqrt {1-x^{2}}}{1+x}}\,,{\text{ if}}-1<x\leq +1\\[0.5em]\arctan x&=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff57584887465d739221d65d55a9c1bd349cb8e)










![{\displaystyle D(\arcsin x)=[-1;1]\qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3f4bf3e28749594b902927c25d875de43acb55)
![{\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35cf0029d59f77e2edbf4e49629cd8563aa42d0b)










![{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8953e7a70dae484772b5a2b5cab77216226235d)







![{\displaystyle D(\arccos x)=[-1;1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91792aac1d518a870d412d3e7d0e9fb7f53e5887)
![{\displaystyle E(\arccos x)=[0;\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc41ed783f7a7698b111ce8f052693448a23a75c)












![{\displaystyle [0;\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45ba33419dc889bf6c0c684b11285afda3437c95)

















































