100 բանտարկյալների խնդիր

100 բանտարկյալի խնդիր, մաթեմատիկական խնդիր հավանականությունների տեսությունում և կոմբինատորիկայում։ Խնդրում 100 համարակալված բանտարկյալներ փրկվելու համար պետք է գտնեն իրենց թիվը 100 տարբեր դարակներում։ Ըստ կանոնների՝ յուրաքանչյուր բանտարկյալ իրավունք ունի բացել 50 դարակ և չի կարող շփվել այլ բանտարկյալների հետ։ Առաջին հայացքից իրավիճակը անհույս է թվում, սակայն որոշ մարտավարությունների դեպքում փրկության բարձր հավանականություն կա։

Դանիացի ինֆորմատիկ Փիթեր Բրո Միլթերսոնը առաջին անգամ ներկայացրել է խնդիրը 2003 թվականին։

Խնդիր[խմբագրել | խմբագրել կոդը]

Գրականության մեջ կան 100 բանտարկյալների խնդրի տարբեր ձևակերպումներ։ Հետևյալ տարբերակը առարաջկել են Ֆիլիպ Ֆլայոլեն և Ռոբերտ Սեջվիկը^[1].

Բանտի տնօրենը մահվան դատապարտված 100 բանտարկյալների, որոնք համարակալված են 1-100 թվերով, առաջարկում է փրկության վերջին հնարավորություն։ Սենյակում կա 100 դարակ ունեցող պահարան։ Տնօրենը յուրաքանչյուր դարակում պատահականության սկզբունքով դնում է բանտարկյալներից մեկի համարը։ Բանտարկյալները իրար հետևից մտնում են սենյակ։ Յուրաքանչյուր բանտարկյալ կարող է բացել և ստուգել 50 կամայական դարակ։ Ստուգելուց հետո դարակները կրկին փակվում են։ Եթե այս որոնման ժամանակ բոլոր բանտարկյալները գտնում են իրենց թիվը, բոլոր բանտարկյալները ներվում են։ Եթե բանտարկյալներից մեկը չի գտնում իր թիվը, բոլոր բանտարկյալները մահվան են դատապարտվում։ Նախքան առաջին բանտարկյալի սենյակ մտնելը, բանտարկյալները կարող են քննարկել և որոշել մարտավորություն, բայց առաջին բանտարկյալի սենյակ մտնելուց հետ միմիյանց հետ շփվելու իրավունք չունեն։ Ո՞րն է լավագույն մարտավարությունը։

Եթե բանտարկյալները դարակները ստուգեն իրարից անկախ և պատահական, ապա մեկ բանտարկյալի կողմից իր թիվը գտնելու հավանականությունը 50% է։ Հետևաբար, հավանականությունը, որ բոլոր բանտարկյալները կգտնեն իրենց թիվը հավասար է բոլոր առանձին հավանականությունների արտադրյալին, որը (12)¹⁰⁰ ≈ 6969800000000000000♠0.0000000000000000000000000000008 է, ինչը չափազանց փոքր թիվ է։

Լուծում[խմբագրել | խմբագրել կոդը]

Մարտավարություն[խմբագրել | խմբագրել կոդը]

Գոյություն ունի մարտավարություն, որի կիրառման դեպքում բանտարկյալների փրկման հավանականությունը ավելի քան 30% է։ Բանտարկյալները չպետք է նախօրոք որոշեն, թե որ դարակներն են բացելու։ Յուրաքանչյուր բանտարկյալ կարող է օգտագործել բացված դարակում եղած ինֆորմացիան, որպեսզի որոշի, թե հաջորդը որ դարակը պետք է բացի։ Կարևոր դիտարկում է այն, որ այս կերպ բանտարկյալների հաջողությունը այլ բանտարկյալների հաջողությունից հավանականորեն անկախ չէ, քանի որ բոլոր կախված են թվերի բաշխումից^[2]։

Մարտավարությունը նկարագրելու համար հարմար է բանտարկյալներից բացի համարակալել նաև դարակները, օրինակ՝ ըստ տողերի՝ սկսած վերևի ձախ անկյունից։ Համարակալումից հետո մարտավարությունը հետևյալն է^[3]՝

Յուրաքանչյուր բանտարկյալ առաջինը բացում է իր թվով համարակալված դարակը,
Եթե այդ դարակում կա իր թիվը, ուրեմն առաջադրանքը ավարտված է հաջողությամբ,
Հակառակ դեպքում բանտարկյալը հաջորը բացում է դարակում գրված թվով դարակը,
Բանտարկյալը կրկնում է 2 և 3 կետերը մինչև իրենց թիվը գտնելը, կամ ձախողվելը, եթե թիվը չի գտնվում առաջին 50 փորձից հետո։

Եթե բանտարկյալը անվերջ փորձերի իրավունք ունենար, նա ի վերջո կբացեր իր դարակը՝ ձևավորելով շղթա։ Սկսելով իր համարի դարակից, բանտարկյալը երաշխավորում է, որ նա գտնվում է այն շղթայում, որի մեջ գտնվում է իր թիվը։ Գոյություն ունի միայն մեկ շղթա, որի երկարությունը 50-ից մեծ է, քանի որ առավելագույնը մեկ շղթա կարող է պարունակել կեսից ավելի դարակներ։

Օրինակներ[խմբագրել | խմբագրել կոդը]

Ստորև ներկայացված է խնդրի պարզեցված տարբերակ, որտեղ կան ընդամենը 8 բանտարկյալներ և դարակներ, բայց յուրաքանչյուր բանտարկյալ կարող է ստուգել 4 դարակ։ Բանտի տնօրենը դարակներում դասավորել է բանտարկյալների թվերը հետևյալ կերպ․

դարակի համար	1	2	3	4	5	6	7	8
բանտարկյալի համար	7	4	6	8	1	3	5	2

Բանտարկյալները այժմ վարվում են հետրյալ կերպ․

Առաջին բանտարկյալը բացում է առաջին դարակը և գտնում յոթ թիվը։ Հետո բացում է յոթերորդ դարակը և գտնում հինգ թիվը։ Հետո բացում է հինգերորդ դարակը, որտեղ գտնում է իր թիվը։
Երկրորդ բանտարկյալը բացում է երկրորդ, չորրորդ և ութերորդ դարակները այս հերթականությամբ։ Վերջին դարակում գտնում է իր թիվը՝ երկուսը։
Երրորդ բանտարկյալը բացում է երրորդ և վեցերորդ դարակները, որտեղ գտնում է իր թիվը։
Չորրորդ բանտարկյալը բացում է չորրորդ, ութերորդ և երկրորդ դարակները, որտեղ գտնում իր թիվը։ Սա նույն շղթան է, որը հանդիպել էր երկրորդ բանտարկյալին և կհանդիպի ութերորդ բանտարկյալին նույնպես։ Այս բանտարկյալներից յուրաքանչյուրը կգտնի իր թիվը երրորդ բացված դարակում։
Հինգերորդ և յոթերորդ բանտարկյալները կգտնեն իրենց թվերը նույն սկզբունքով։

Այս օրինակում բոլոր բանտարկյալները գտան իրենց թվերը։ Սակայն, միշտ չէ, որ դա հնարավոր է։ Օրինակ՝ եթե հինգերորդ և ութերորդ դարակների թվերը փոխարինեք միմիյանց հետ, առաջին բանտարկյալը չի կարողանա գտնել իր թիվը առաջին, յոթերորդ, հինգերորդ և երկրորդ դարակները բացելուց հետո․

դարակի համար	1	2	3	4	5	6	7	8
բանտարկյալի համար	7	4	6	8	2	3	5	1

Իսկ հետևյալ դասավորության դեպքում առաջին բանտարկյալը բացում է առաջին, երրորդ, յոթերորդ և չորրորդ դարակները, որից հետո ձախողվում է․

դարակի համար	1	2	3	4	5	6	7	8
բանտարկյալի համար	3	1	7	5	8	6	4	2

Ընդ որում, այս դասավորության դեպքում վեցերորդ բանտարկյալից բացի բոլորը ձախողվում են։

Տեղափոխությամբ ներկայացում[խմբագրել | խմբագրել կոդը]

Տեղափոխության ներկայացումը գրաֆի տեսքով (1 7 5)(2 4 8)(3 6) և (1 3 7 4 5 8 2)(6)

Տնօրենի կողմից դարակներին բանարկյալների թիվ նշանակելը մաթեմատիկորեն կարելի է ներկայացնել որպես 1-100 թվերի տեղափոխություն։ Նման տեղափոխությունը 1-100 բնական թվերի բազմության փոխմիարժեք համապատասխանություն է ինքն իր հանդեպ։ Թվերի հաջորդականությունը, որը շարունակական տեղափոխությունից հետո վերադառնում է առաջին թվին կոչվում է տեղափոխության ցիկլ։ Յուրաքանչյուր տեղափոխություն կարելի է բաժանել տարանջատ ցիկլերի, այսինքն՝ ցիկլերի, որոնք չունեն ընդհանուր տարր։ Վերևի առաջին օրինակի տեղափոխությունը կարելի է ներկայացնել հետևյալ կերպ

(1~7~5)(2~4~8)(3~6)

որը կազմված է 3 երկարությամբ երկու և 2 երկարությամբ մեկ ցիկլից։ Երրորդ օրինակի տեղափոխությունը կունենա հետևյալ տեսքը՝

(1~3~7~4~5~8~2)(6)

որը կազմված է 7 և 1 երկարություններ ունեցող մեկական ցիկլերից։ Այս նշանակումը եզակի չէ, քանի որ $l$ երկարությամբ ցիկլը կարելի է գրել $l$ տարբեր ձևով՝ կախված ցիկլի առաջին թվից։ Դարակները բացելու ընթացքում յուրաքանչյուր բանտարկյալ հետևում է մեկ ցիկլի, որը միշտ ավարտվում է իրենց թվով։ Ութ բանտարկյալների դեպքում այս մարտավարությունը հաջողվում է այն և միայն այն դեպքում, երբ ամենաերկար ցիկլի երկարությունը չի գերազանցում 4-ը։ Եթե տեղափոխությունը պարունակում է 5 կամ ավել երկարություն ունեցող ցիկլ, ապա բոլոր այն բանտարկյալները, որոնց թիվը գտնվում է այդ ցիկլում չեն գտնում իրենց թիվը առաջին չորս քայլից հետո։

Հաջողության հավանականություն[խմբագրել | խմբագրել կոդը]

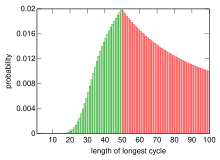
Նախնական խնդրում 100 բանտարկյալներին հաջողվում է փրկվել, եթե տեղափոխության ամենաերկար ցիկլի երկարությունը չի գերազանցում 50-ը։ Հետևաբար, իրենց փրկվելու հավանականությունը հավասար է հավանականությանը, որ 1-ից 100 թվերի պատահական տեղափոխությունը չի փարունակում 50-ից մեծ երկարություն ունեցող ցիկլ։ Այս հավանականությունը կարելի է հաշվել հետևյալ կերպ։

1-ից 100 թվերի տեղափոխությունը կարող է պարունակել առավելագույնը մեկ $l>50$ երկարությամբ ցիկլ։ Գոյություն ունի այդ ցիկլի տարրեը ընտրելու ճիշտ ${\tbinom {100}{l}}$ տարբերակ (տես՝ ընտրույթ)։ Այս ցիկլում թվերը կարող են դասավորվել $(l-1)!$ ձևով, քանի որ $l$ երկարություն ունեցող իրարից տարբեր ցիկլերը կարելի է ներկայացնել $l$ տեղափոխությամբ՝ ցիկլերի սիմետրիայի պատճառով։ Մնացած թվերը կարելի է դասավորել $(100-l)!$ ձևով։ Հետևաբար, 1-ից 100 թվերի $l>50$ երկարություն ունեցող տեղափոխությունների քանակը հավասար է

{\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}

։

Հավանականությունը, որ հավասարաչափ բաշխված պատահական տեղափոխությունը չի ունենա 50-ից մեծ երկարություն ունեցող ցիկլ հաշվվում է պատահույթի և այդ պատահույթի լրույթի բանաձևով․

1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183,

որտեղ $H_{n}$ -ը $n$ -րդ հարմոնիկ թիվն է։ Հետևաբար, ցիկլին հետևող մարտավարությամբ բանատրկյալները փրկվում են ավելի քան 31% դեպքերում^[3]։

Ասիմպտոտիկ հավանականություն[խմբագրել | խմբագրել կոդը]

Եթե 100-ի փոխարեն դիտարկվում է $2n$ բանտարկյալ, որտեղ $n$ -ը կամայական բնական թիվ է, ապա այս մարտավարությունը կիրառելու դեպքում բանտարկյալների փրկության հավանականությունը տրվում է հետևյալ կերպ՝

1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2

։

Օգտվելով Էյլեր-Մասկերոնի $\gamma$ հաստատունից և դիրատկելով $n\to \infty$ սահմանաը, ստանում ենք՝

\lim _{n\to \infty }(H_{n}-\ln n)=\gamma

որից հետևում է, որ փրկման ասիմպտոտիկ հավանականությունը հավասար է՝

\lim _{n\to \infty }(1-H_{2n}+H_{n})=1-\gamma +\gamma -\ln 2=1-\ln 2\approx 0.30685

։

Քանի որ հավանականությունների հաջորդականությունը մոնոտոն նվազում է, հետևաբար այս մարտավարությամբ բանտարկյալները փրկվում են ավելի քան 30% դեպքերում՝ անկախ բանտարկյալների քանակից^[3]։

Օպտիմալություն[խմբագրել | խմբագրել կոդը]

2006 թվականին Յուջին Կուրտինը և Մաքս Վարշաուերը ապացուցեցին, որ ցիկլին հետևելու մարտավարությունը օպտիմալ է։ Ապացույցը հիմնված է այս և առնչվող խնդրի, որտեղ բանտարկալները իրավունք ունեն ներկա գտնվել սենյակում և տեսնել դարակների բացումը, համարժեքության վրա։ Մաթեմատիկորեն այս համարժեքությունը հիմնված է Ֆոատայի լեմմայի վրա (ցիկլերի կանոնական նշանակման և տեղափոխությունների նշանակման փոխմիարժեք համապատասխանություն)։ Երկրորդ խնդրում փրկության հավանականությունը կախված չէ ընտրված մարտավարությունից և հավասար է նախնական խնդրի հավանականությանը, եթե այն լուծելու համար կիրառվի ցիկլին հետևելու մարտավարությունը։ Քանի որ նախնական խնդրի կամայական մարտավարություն կարելի է կիրառել երկրորդ խնդրի համար, բայց այն չի կարող ունենալ ավելի բարձր փրկման հավանականություն, ուրեմն ցիկլին հետևելու մարտավարությունը օպտիմալ է^[4]։

Պատմություն[խմբագրել | խմբագրել կոդը]

100 բանտարկյալների խնդիրն առաջին անգամ դիտարկել է դանիացի ինֆորմատիկ Փիթեր Բրո Միլթերսոնը 2003 թվականին։ Նա այն հրատարակել է Աննա Գալի հետ «30. Ավտոմատների, լեզուների և ծրագրավորման միջազգային կոլոքվիումի» (անգլ.՝ 30. International Colloquium on Automata, Languages and Programming, (ICALP)) աշխատություններում^[5]։ Իրենց տարբերակում առաջին խաղացողը (թիմ Ա) պատահական գունավորում է Բ թիմի անդամների անուններով թղթի կտորները կարմիր կամ կապույտ և տեղադրում տարբեր տուփերում։ Որոշ տուփեր դատարկ են (տես ներքևում)։ Հաղթելու համար Բ թիմից յուրաքանչյուրը տուփերի կեսը բացելուց հետո պետք է գուշակի իր գույնը^[5]։ Սկզբում Միլթերսոնը ենթադրել է, որ հաղթելու հավանականությունը արագ ձգտում է զրոյի, երբ խաղացողների քանակը ձգտում է անվերջության։ Սական, Սվեն Սքյումը, որը Օրհուսի համալսարանում Միլթերսոնի կոլեգան էր, առաջարկել է ցիկլին հետևելու մարտավարությունը խնդրի այն դեպքի համար, երբ դատարկ տուփեր չկան։ Հրատարակությունում այս պարտավարությունը գտնելը հանձնարարված էր որպես վարժություն։ Հոդվածը ստացել լավագույն հոդվածի մրցանակ^[4]։

2004 թվականի ամռանը խնդիրը հայտնվել է Մաթեմատիկական գիտությունների գիտահետազոտական ինստիտուտի կողմից հրատարակվող «Էմիսարը» (անգլ.՝ The Emissary) եռամսյա հանդեսի Ջո Բուլերի և Էլվին Բեռլեկեմպի կողմից գլուխկոտրուկների բաժնում։ Այնտեղ հեղինակները տուփերը փոխարինել են ROM-ներով (միայն կարդալու հիշողություն), իսկ մասնակիցների համարով գունավորված թղթերը՝ մասնակիցների թիվը դրական կամ բացասական նշանով։ Հեղինակները նշել են, որ հաղթելու հավանականությունը կարելի է մեծացնել նույնիսկ այն դեպքում, երբ առաձին խաղացողը չի գտնում իր թիվը։ Դրան հասնելու համար, յուրաքանչյուր անդամ է հաշվի բոլոր բացված տուփերում նշանների արտադրյալը, և եթե վերջում նրան չի հաջողվում գտնել իր թիվը, խաղացողը պետք է ենթադրի, որ իր թիվը ունի հաշվված նշանը։ Չնայած այս ենթադրությունը ճիշտ է միայն 50% դեպքերում, եթե ցիկլի երկարությունը $1+\lfloor n/2\rfloor$ է, ապա բոլոր խաղացողները միաժամանակ կա՛մ ճիշտ կլինեն, կա՛մ սխալ։ Մարտավարության այս փոփոխությունը զգալի առավելություն է տալիս փոքր քանակով խաղացողների դեպքում, բայց աննշան է մեծ թվով խաղացողների դեպքում^[6]։

Հաջորդ տարիներին խաղը մտել է մաթեմատիկական գրականության մեջ, որտեղ ներկայացվել է տարբեր տեսքերով, ինչպես օրինակ՝ սեղանին քաղաքարտերով^[7] կամ պահարաններում դրամապանակներով^[4]։ Բանտարկյալների տեսքով այն հրատարակվել է 2006 թվականին Քրիստոֆ Պոպպեի կողմից «Scientific American»-ում և Փիթեր Ուինքլերի կողմից «College Mathematics Journal»-ում^[8]^[9]։ Փոքր փոփոխություններով Ֆիլիպ Ֆլայոլեն, Ռոբերտ Սեջվիկը և Ռիչարդ Պ. Սթենլին օգտագործել են այս խնդիրը իրենց կոմբինատորիկայի դասագրքում^[1]^[3]։

Տարբերակներ[խմբագրել | խմբագրել կոդը]

Դատարկ տուփեր[խմբագրել | խմբագրել կոդը]

ՍԿզբում Գալն ու Միլթերսենը իրենց հոդվածում դիտարկել են այն դեպքը, երբ տուփերի քանակը երկու անգամ մեծ է երկրորդ թիմի անդամների քանակից, բայց տուփերի կեսը դատարկ է։ Սա ավելի բարդ խնդիր է, քանի որ դատարկ տուփերը ոչ մի տեղ չեն ուղղորդում, հետևաբար ցիկլին հետևելու մարտավարությունը չի կարող կիրառվել։ Հայտնի չէ, թե արդյոք այս դեպքում հաղթելու հավանականությունը ձգտում է զրոյի, երբ խաղացողների քանակը ձգտում է անվերջության^[5]։

2005 թվականին Նավին Գոյալը և Մայքլ Սաքսը ավելի ընդհանուր խնդրի համար, որտեղ դատարկ տուփերի և թիմի յուրաքանչյուր անդամին թույլատրվող փորձերի քանակը փոփոխական է, մշակել են մարտավարություն՝ հիմնվելով ցիկլին հետևելու մարտավարության վրա։ Այս դեպքում նույնպես հաղթելու հավանականությունը ձգտում է զրոյի, բայց ավելի դանդաղ, քան Գալն ու Միլթերսենը առաջարկել էին։ Եթե խաղացողների քանակն ու թույլատրելի փորձերի հարաբերությունը ֆիքսված է, փրկվելու հավանականությունը մեծ է զրոյից, երբ ավելի շատ դատարկ տուփեր են ավելացվում^[10]։

2009 թվականին Դեյվիդ Ավիսը և Էնն Բրոդբենտը դիտարկել են խնդրի քվանտային տարբերակ, որտեղ երկրորդ թիմի անդամները վստահաբար հաղում են^[11]։

Չարամիտ տնօրեն[խմբագրել | խմբագրել կոդը]

Եթե տնօրենը պարտավոր չէ թվերը դարակներում պատահական բաշխել, և տեղյակ է, որ բանտարկյալները պատրաստվում են կիրառել վերևում նշված մարտավարությունը, նա կարող է ձախողել մարտավարությունը։ Դրա համար տնօրենը պարզապես պետք է համոզվի, որ դարակներում բանտարկյալների թվերը 50-ից մեծ ցիկլով տեղափոխություն են կազմում։ Այս դեպքում բանտարկյալները կարող են պարզապես համաձայնվել և դարակները պատահականության սկզբունքով վերահամարակալել^[12]։

Բանտարկյալների մեկը կարող է մեկ փոփոխություն անել[խմբագրել | խմբագրել կոդը]

Այն դեպքում, երբ բանտարկյալներից մեկը կարող է սկզբում մտնել սենյակ, ստուգել բոլոր դարակները և փոխանակել երկու դարակի պարունակությունը, բոլորը բանտարկյալները միշտ փրկվում են։ Այս պնդումը ճիշտ է, քանի որ 50-ից մեծ երկարություն ունեցող կամայական ցիկլ հնարավոր է կոտրել այնպես, որ բոլոր ցիկլերը 50-ից փոքր երկարություն ունենան։

Իր թիվը գտնող յուրաքանչյուր բանտարկյալ փրկվում է[խմբագրել | խմբագրել կոդը]

Այն դեպքում, երբ իր թիվը գտնող յուրաքանչյուր բանտարկյալ ազատ է արձակվում, կամայական բանտարկյալի փրկվելու սպասվող հավանականությունը հետևյալն է (եթե տեղափոխությունը պատահական է).

առանց պարտավարության՝ ${\frac {1}{2}}$ ,

սկզբնական խնդրի մարտավարությամբ՝ $(1-\ln(2))\cdot 1+\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}\left(1-{\frac {k}{n}}\right)=1-\ln(2)+\sum _{\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}-\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{n}}=1-\ln(2)+\ln(2)-{\frac {1}{2}}={\frac {1}{2}}:$

Պետք է նշել, որ չնայած այս սպասումները նույն արժեքն ունեն, դրանք տարբեր բաշխումներից են։ Երկրորդ մարտավարության դեպքում որոշ բանտարկյալների մահը կամ փրկվելը նախորոշված է տրված տեղափոխության դեպքում, մինչդեռ առաջին մարտավարության դեպքում (պատահական ընտրություն) անկախ տեղափոխությունից յուրաքաչյուր բանտարկյալ ունի փրկվելու 1/2 շանս։

Մոնտի Հոլի խնդիր[խմբագրել | խմբագրել կոդը]

2009 թվականին Ադամ Ս. Լանդսբերգը առաջարկել է 100 բանտարկյալների խնդրի հետևյալ տարբերակը, որը հիմնված է հայտնի Մոնտի Հոլի պարադոքսի վրա^[13].

Երեք փակ դռների հետևում պատահական բաշխված են մեքենա, մեքենայի բանալի և այծ։ Կան երկու խաղացողներ. առաջին խաղացողը պետք է գտնի մեքենան, երկրորդը՝ մեքենայի բանալին։ Խաղացողները շահում են մեքենան միայն այն դեպքում, երբ երկուսն էլ հաղջությամբ գտնում են իրենց մասը։ Առաջին խաղացողը մտնում է սենյակ և կարող է բացել երեք դռներից մեկը։ Եթե առաջինը հաջողությամբ գտնում է մեքենան, դռները նորից փակվում են և երկրորդ խաղացողն է մտնում սենյակ։ Երկրորդ խաղացողը նույնպես կարող է բացել երկու դուռ, բայց խաղացողները չեն կարող հաղորդակցվել միմիայնց հետ։ Ինչքա՞ն է հաղթելու հավանականությունը, եթե երկու խաղացողներն էլ օպտիմալ վարվեն։

Եթե խաղացողները դռները պատահական բացեն, ապա հաղթելու հավանականությունը 49 (մոտ 44%) է։ Սակայն, օպտիմալ մարտավարությունը հետևյալն է.

Առաջին խաղացողը սկզբում բացում է առաջին դուռը։ Եթե մեքենան առաջին դռան հետևում է, ուրեմն առաջին խաղացողին հաջողվեց գտնել մեքենան։ Եթե առաջին դռան հետևում մեքենայի բանալին է, ուրեմն խաղացողը հաջորդը բացում է երկրորդ դուռը, իսկ եթե առաջին դռան հետևում այծն է, առաջին խաղացողը հաջորդը բացում է երրորդ դուռը։
Երկրորդ խաղացողը սկզբում բացում է երկրորդ դուռը։ Եթե մեքենայի բանալին երկրորդ դռան հետևում է, ուրեմն երկրորդ խաղացողին հաջողվեց գտնել մեքենայի բանալին։ Եթե երկրորդ դռան հետևում այծ է, ուրեմն խաղացողը հաջորդը բացում է երրորդ դուռը, իսկ եթե երկրորդ դռան հետևում մեքենան է, ուրեմն խաղացողը բացում է առաջին դուռը։

Մեքենայի, մեքենայի բանալու և այծի հնարավոր վեց բաշխումների դեպքում խաղացողները բացում են հետևյալ դռները (կանաչ դեպքերում խաղացողին հաջողվել է գտնել իր իրը).

	Մեքենա − Բանալի − Այծ	Մեքենա − Այծ − Բանալի	Բանալի − Մեքենա − Այծ	Բանալի − Այծ − Մեքենա	Այծ − Մեքենա − Բանալի	Այծ − Բանալի − Մեքենա
Խաղացող 1	Դուռ 1։ Մեքենա	Դուռ 1։ Մեքենա	Դուռ 1։ Բանալի Դուռ 2։ Մեքենա	Դուռ 1։ Բանալի Դուռ 2։ Այծ	Դուռ 1։ Այծ Դուռ 3։ Բանալի	Դուռ 1։ Այծ Դուռ 3։ Մեքենա
Խաղացող 2	Դուռ 2։ Բանալի	Դուռ 2։ Այծ Դուռ 3։ Բանալի	Դուռ 2։ Մեքենա Դուռ 1։ Բանալի	(Դուռ 2։ Այծ) (Դուռ 3։ Մեքենա)	(Դուռ 2։ Մեքենա) (Դուռ 1։ Այծ)	Դուռ 2։ Բանալի

Այս մարտավարության հաջողությունը հիմնված է խաղացողների հաջողության և ձախողման միջև կորելացիա ստեղծելու վրա։ Այստեղ, հաղթելու հավանականությունը 23 է, որը օպտիմալ է, քանի որ առաջին խաղացողը չի կարող դրանից ավելի բարձր հաղթելու հավանականություն ունենալ^[13]։ Այլ տարբերակներում երեք մրցանակներ թաքնված են երեք դռների հետևում և երեք խաղացողներ պետք է գտնեն իրենց նշանակված մրցանակը։ Այս դեպքում ևս հաղթելու հավանականությունը 23 է, երբ կիրառվում է օպտիմալ մարտավարություն^[14]։

Կենտ թվով հնարավորություններ[խմբագրել | խմբագրել կոդը]

Խնդրի տարբերակներից մեկում բանտարկյալները իրենց թվերը պետք է գտնեն ոչ թե առաջին 50 փորձի ընթացքում, այլ պետք է գտնեն կենտ համարով փորձի ժամանակ $1, 3, ..., 97, 99$ : Այս դեպքում ևս ցանկացած բանտարկյալ ունի հաջողելու 50% հնարավորություն։ Հիմնական մարտավարությունը կաշխատի, եթե բանտարկյալների տեղափոխությունը ունի միայն կենտ երկարությամբ ցիկլեր։ 100 բանտարկյալների և հիմնական մարտավարության դեպքում փրկվելու հավանականությունը 7.9589% է, որը զգալիորեն մեծ է պատահական ընտրության դեպքում փրկվելու հավանականությունից` $(1/2) 100$ -ից։

Տես նաև[խմբագրել | խմբագրել կոդը]

Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]

↑ ^1,0 ^1,1 Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, էջ 124
↑ Eugene Curtin, Max Warshauer (2006), «The locker puzzle», Mathematical Intelligencer, 28: 28–31, doi:10.1007/BF02986999, S2CID 123089718
↑ ^3,0 ^3,1 ^3,2 ^3,3 Richard P. Stanley (2013), Algebraic Combinatorics: Walks, Trees, Tableaux, and More, Springer, էջեր 187–189
↑ ^4,0 ^4,1 ^4,2 Eugene Curtin, Max Warshauer (2006), «The locker puzzle», Mathematical Intelligencer, 28: 28–31, doi:10.1007/BF02986999, S2CID 123089718
↑ ^5,0 ^5,1 ^5,2 Anna Gál, Peter Bro Miltersen (2003), «The cell probe complexity of succinct data structures», Proceedings 30th International Colloquium on Automata, Languages and Programming (ICALP), էջեր 332–344
↑ Joe Buhler, Elwyn Berlekamp (2004), «Puzzles Column», The Emissary, Spring 2004: 3, Արխիվացված օրիգինալից 2023 թ․ հուլիսի 5-ին, Վերցված է 2024 թ․ փետրվարի 9-ին
↑ Richard E. Blahut (2014), Cryptography and Secure Communication, Cambridge University Press, էջեր 29–30
↑ Christoph Pöppe (2006), «Mathematische Unterhaltungen: Freiheit für die Kombinatoriker», Spektrum der Wissenschaft (german), 6/2006: 106–108, Արխիվացված օրիգինալից 2014 թ․ դեկտեմբերի 21-ին, Վերցված է 2024 թ․ փետրվարի 9-ին{{citation}}: CS1 սպաս․ չճանաչված լեզու (link)
↑ Peter Winkler (2006), «Names in Boxes Puzzle», College Mathematics Journal, 37 (4): 260, 285, 289
↑ Navin Goyal, Michael Saks (2005), «A parallel search game», Random Structures & Algorithms, 27 (2): 227–234, doi:10.1002/rsa.20068, S2CID 90893
↑ David Avis, Anne Broadbent (2009), «The quantum locker puzzle», Third International Conference on Quantum, Nano and Micro Technologies ICQNM '09, էջեր 63–66
↑ Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, էջ 177
↑ ^13,0 ^13,1 Adam S. Landsberg (2009), «The Return of Monty Hall», Mathematical Intelligencer, 31 (2): 1, doi:10.1007/s00283-008-9016-8
↑ Eric Grundwald (2010), «Re: The Locker Puzzle», Mathematical Intelligencer, 32 (2): 1, doi:10.1007/s00283-009-9107-1

Գրականություն[խմբագրել | խմբագրել կոդը]

Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, ISBN 978-1-139-47716-1
Richard P. Stanley (2013), Algebraic Combinatorics: Walks, Trees, Tableaux, and More, Undergraduate Texts in Mathematics, Springer, ISBN 978-1-461-46998-8
Peter Winkler (2007), Mathematical Mind-Benders, Taylor and Francis, ISBN 978-1-568-81336-3

Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]

Rob Heaton: Mathematicians hate civil liberties - 100 prisoners and 100 boxes, 13 January 2014
Oliver Nash: Pity the prisoners Արխիվացված 2014-07-14 Wayback Machine, 12 December 2009
Jamie Mulholland: Prisoners in Boxes, Spring 2011 (PDF)
MinutePhysics: An Impossible Bet ՅուԹյուբում and Solution to The Impossible Bet ՅուԹյուբում, 8 December 2014
Veritasium: The Riddle That Seems Impossible Even If You Know The Answer ՅուԹյուբում, 20 June 2022
Robert Feldt: Stochastic simulation in Julia to check the optimal strategy, 6 July 2022

[flajolet-1] 1,0 ^1,1 Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, էջ 124

[curtin2-2] Eugene Curtin, Max Warshauer (2006), «The locker puzzle», Mathematical Intelligencer, 28: 28–31, doi:10.1007/BF02986999, S2CID 123089718

[stanley-3] 3,0 ^3,1 ^3,2 ^3,3 Richard P. Stanley (2013), Algebraic Combinatorics: Walks, Trees, Tableaux, and More, Springer, էջեր 187–189

[curtin-4] 4,0 ^4,1 ^4,2 Eugene Curtin, Max Warshauer (2006), «The locker puzzle», Mathematical Intelligencer, 28: 28–31, doi:10.1007/BF02986999, S2CID 123089718

[miltersen-5] 5,0 ^5,1 ^5,2 Anna Gál, Peter Bro Miltersen (2003), «The cell probe complexity of succinct data structures», Proceedings 30th International Colloquium on Automata, Languages and Programming (ICALP), էջեր 332–344

[buhler-6] Joe Buhler, Elwyn Berlekamp (2004), «Puzzles Column», The Emissary, Spring 2004: 3, Արխիվացված օրիգինալից 2023 թ․ հուլիսի 5-ին, Վերցված է 2024 թ․ փետրվարի 9-ին

[7] Richard E. Blahut (2014), Cryptography and Secure Communication, Cambridge University Press, էջեր 29–30

[pöppe-8] Christoph Pöppe (2006), «Mathematische Unterhaltungen: Freiheit für die Kombinatoriker», Spektrum der Wissenschaft (german), 6/2006: 106–108, Արխիվացված օրիգինալից 2014 թ․ դեկտեմբերի 21-ին, Վերցված է 2024 թ․ փետրվարի 9-ին{{citation}}: CS1 սպաս․ չճանաչված լեզու (link)

[winkler-9] Peter Winkler (2006), «Names in Boxes Puzzle», College Mathematics Journal, 37 (4): 260, 285, 289

[10] Navin Goyal, Michael Saks (2005), «A parallel search game», Random Structures & Algorithms, 27 (2): 227–234, doi:10.1002/rsa.20068, S2CID 90893

[11] David Avis, Anne Broadbent (2009), «The quantum locker puzzle», Third International Conference on Quantum, Nano and Micro Technologies ICQNM '09, էջեր 63–66

[12] Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, էջ 177

[landsberg-13] 13,0 ^13,1 Adam S. Landsberg (2009), «The Return of Monty Hall», Mathematical Intelligencer, 31 (2): 1, doi:10.1007/s00283-008-9016-8

[14] Eric Grundwald (2010), «Re: The Locker Puzzle», Mathematical Intelligencer, 32 (2): 1, doi:10.1007/s00283-009-9107-1

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]