Ոսկե ուղղանկյուն
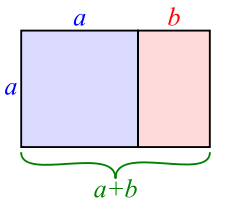
Ոսկե ուղղանկյուն, ուղղանկյուն, որի կողմերի երկարությունները գտնվում են ոսկե համեմատականության մեջ , կամ (հունական ֆի տառը), որտեղ φ ≈ 1,618.
Կառուցում[խմբագրել | խմբագրել կոդը]

Ոսկե ուղղանկյուն կարելի է կառուցել կարկինի և քանոնի օգնությամբ։
- Կառուցում ենք սովորական քառակուսի։
- Գագաթից տարվում է ուղիղ մինչև հանդիպակաց կողմի միջնակետը։
- կառուցում ենք շրջանագիծб հատման կետը ընդունելով որպես կենտրոն, շառավղի չափ ենք ընդունում ստացված հատվածի երկարությունը։
- Շարունակում ենք հանդիպակաց կողմըб մինչև հատվի շրջանագծի հետ։
Կապը կանոնավոր բազմանիստերի և բազմանկյունների հետ[խմբագրել | խմբագրել կոդը]
Առանձնահատկությունը կայանում է նրանում, որ քառակուսին հեռացնելուց հետո մնում է ոսկե ուղղանկյուն, պահպանելուվ նույն չափերը։ Քառակուսիների հեռացումը կարող է լինել անվերջ, ընդվորում համապատասխան անկյունները կազմում են անվերջ ոսկե պարույրի(բնական լոգարիթմական պարույր այդ հատկությունով) վրա գտնվող կետերի շարք։

Այլ ձևով կառուցելու համար օգտագործում են միանման շրջանագծերոմ ներգծված երեք կանոնավոր բազմանկյուններ՝ տասնանկյուն, վեցանկյուն և հնգանկյուն։ Այդ բազմանկյունների a, b և c կողմերի երկարությունները բավարարում են a 2 + b2 = c2 հավասարմանը, այնպես, որ այդ երկարությամբ հատվածները կազմում են յուրահատուկ ուղղանկյուն եռանկյուն(Պյութագորասի թեորեմի համաձայն)։ Վեցանկյան կողմի երկարության հարաբերությունը տասնանկյան կողմի երկարությանը հավասար է ոսկե հատմանը, այնպես, որ եռանկյունը կազմում է ոսկե ուղղանկյան կեսը[1]։
Իկոսաեդրի տասներկու գագաթները կարելի է բաժանել երեք փոխադարձ ուղղահայաց ոսկե ուղղանկյունների, որոնց սահմանները պատկերում են Բորոմեոյի օղակները[2]։
Հավելված[խմբագրել | խմբագրել կոդը]
Համաձայն աստղաֆիզիկայի և մաթեմատիկայի հանրայնացնող Մարիո Լիվիոյի, Պաչոլիի[3]«Աստվածային համեմատականություն»(1509 թվական[4]), երբ ոսկե համեմատականությունը հայտնի դարձավ նկարիչներին, առանց ավելորդ մաթեմատիկայի[5] , շատ արվեստագետներ հիացած էին ոսկե հատույթով, համարելուվ դա էսթետիկորեն հաճելի երևույթ։ Այնպիսի ճարտարապետական գլուխգործոցները, ինչպիսիք են Պարթենոնը Աթենքում, կամ Գրանադայի Ալգեմբրան, ակնհայտորեն օգտագործվել է ոսկե ուղղանկյան հարաբերակցությունները։
- Ճարտարապետ Լե Կարբյուզեի կառուցած Շտեյնի առանձնատունը (1927թվական)՝ հորիզոնական, արտաքին կամ ներքին կառուցման մեջ օգտագործված է ոսկե ուղղանկյան հարաբերակցություններին մոտ հարաբերակցությունները [6]։
- Տոգոյի դրոշը նույնպես, մշակված է ոսկե ուղղանկյան հարաբերակցությանը մոտ հարաբերակցությամբ[7]։
Տես նաև[խմբագրել | խմբագրել կոդը]
- Ֆիբոնաչիի թվեր
- Ոսկե միջին
- Ոսկե հատում
- Ոսկե շեղանկյուն
- Կեպլերի եռանկյուն
- Արծաթե հատում
Ծանոթագրություն[խմբագրել | խմբագրել կոդը]
- ↑ Euclid, Book XIII, Proposition 10.
- ↑ Burger, Starbird, 2005, էջ 382
- ↑ Van Mersbergen, 1998
- ↑ Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
- ↑ Livio, 2002
- ↑ Padovan, 1999, էջ 320
- ↑ «Flag of Togo». FOTW.us. Flags Of The World. Արխիվացված է օրիգինալից 2007 թ․ հունիսի 7-ին. Վերցված է 2007 թ․ հունիսի 9-ին.
Գրականություն[խմբագրել | խմբագրել կոդը]
- Edward B. Burger, Michael P. Starbird The Heart of Mathematics: An Invitation to Effective Thinking. — Springer, 2005. — ISBN 9781931914413
- Mario Livio The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. — New York: Broadway Books, 2002. — ISBN 0-7679-0815-5
- Audrey M. Van Mersbergen Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic // Communication Quarterly. — 1998. — Т. 46. 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.
- Le Corbusier The Modulor. — С. 35., как цитировано у Падована Richard Padovan Proportion: Science, Philosophy, Architecture. — Taylor & Francis, 1999. — С. 320.: "Both the paintings and the architectural designs make use of the golden section".
- JoJo bizare adventure "Stell ball run"-Arraki-
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- Golden Ratio at MathWorld
- The Golden Mean and the Physics of Aesthetics Արխիվացված 2015-03-30 Wayback Machine
- Golden rectangle demonstration Ինտերակտիվ անիմացիաներով



