Հնգանկյուն

Հնգանկյուն, բազմանկյուն հինգ անկյուններով։ Այդպես են անվանում նաև նմանատիպ տեսք ունեցող ցանկացած առարկա։

Ուռուցիկ հնգանկյուն[խմբագրել | խմբագրել կոդը]

Ուսռուցիկ կոչվում է այն հնգանկյունը, որի բոլոր կողմերն ընկած են կողմերից կամայականն ընդգրկող ուղղի մի կողմում։

Ուռուցիկ հնգանկյան բոլոր ներքին անկյունների գումարը 540° է։

\sum {\alpha =}(n-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }

Յուրաքանչյուր կամայական 9 կետեր պարունակում են ուռուցիկ հնգանկյան գագաթներ, բայց կան 8 կամայական կետերի այնպիսի խմբեր, որոնցում չկան հնգանկյան գագաթներ^[1]։. Նաև ապացուցված է, որ հարթության մեջ ցանկացած 10 կետեր պարունակում են հնգանկյուն, նաև, կան այնպիսի 9 կետերի դասավորություններ, որոնք չեն պարունակում հնգանկյուն^[1].։

Կառուցում[խմբագրել | խմբագրել կոդը]

Կանոնավոր հնգանկյուն[խմբագրել | խմբագրել կոդը]

Պենտագոն կամ կանոնավոր հնգանկյուն կոչվում է այն հնգանկյունը, որի բոլոր կողմերն ու գագաթները հավասար են։ Եթե տանենք հնգանկյան անկյունագծերը, ապա կստացվի^[2]

փոքր պենտագոն (որն առաջանում է անկյունագծերի հատման կետերով)՝ կենտրոնում։
Փոքր պենտագոնի շուրջը հինգ հավասարասրուն եռանկյուն երկու տեսակի (սրունքի ու նհիմքի հարաբերիությունը հավասար է ոսկե չափին)․
- 1) ունեն 36° աստիճանի հավասար անկյուններ գագաթում և 72° աստիճանային չափով անկյուններ հիմքին առընթեր։
- 2) ունեն 108° անկյուն գագաթում և հիմքին առընթեր 36° աստիճանի անկյուններ։

Երկու առաջին և երկու երկրորդ եռանկյունների իրենց հիմքերով միացման դեպքում առաջանում են երկու «ոսկե» շեղանկյուններ (առաջինն ունի 36° սուր անկյուն և 144° բութ անկյուն)։ Ռոջեր Պենրոուզը օգտագորշել է «ոսկե» շեղանկյունները «ոսկե» մանրահատակի համկար (Պենրոուզի խճանկար)։

Աստղաձև հնգանկյուններ[խմբագրել | խմբագրել կոդը]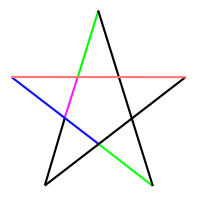

Բազմանկյունը, որի երկու կողմերն ուն երկու անկյունները հավասար են, իսկ օգագաթները համընկնում են կանոնավոր բազմանկյան գագաթների հետ, կոչվում է աստղաձև։ Կանոնավորի հետ մեկտեղ գոյություն ունի ևս մեկ աստղաձև հնգանկյուն՝ պենտագրամա։

Պենտագրաման, ինչպես ենթադրում էր Պյութագորասը, իրենից ներկայացնում է մաթեմատիկական կատարելություն, քանի որ դեմոնստրացնում է ոսկե հատումը (φ = (1+√5)/2 = 1,618…)։ Եթե յուրաքանչյուր գունավոր հատվածի երկարությունը բաժանենք մնացած հատվածներից ամենամեծի վրա, ապա կստացվի φ։

\varphi ={\frac {\mathrm {\color {red}red} }{\mathrm {\color {Blue}blue} }}={\frac {\mathrm {\color {Blue}blue} }{\mathrm {\color {Green}green} }}={\frac {\mathrm {\color {Green}green} }{\mathrm {\color {Magenta}magenta} }}

Հնգանկյունների օրինակներ[խմբագրել | խմբագրել կոդը]

Բույսեր[խմբագրել | խմբագրել կոդը]

Կենդանիներ[խմբագրել | խմբագրել կոդը]

Ճարտարապետության մեջ[խմբագրել | խմբագրել կոդը]

Հնգանկյունները բազմանիստերում[խմբագրել | խմբագրել կոդը]


Դոդեկաեդր	Pyritohedron	Պենտագոնալ իկոսատետրաեդր	Պենտագոնալ հեքսակոնտաեդր	Truncated trapezohedron

Տես նաև[խմբագրել | խմբագրել կոդը]

Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]

↑ ^1,0 ^1,1 Kalbfleisch, J.D.; Kalbfleisch, J.G.; Stanton, R.G. (1970), «A combinatorial problem on convex regions», Proc. Louisiana Conf. Combinatorics, Graph Theory and Computing, Congressus Numerantium, 1, Baton Rouge, La.: Louisiana State Univ., pp. 180–188
↑ Պենրոուզի սալիկներ

Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]

Տես՝ Պենտագոն Վիքիբառարան, բառարան և թեզաուրուս

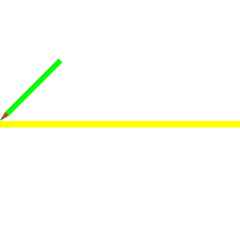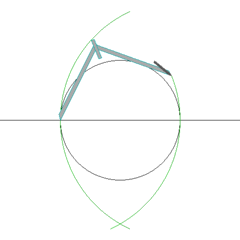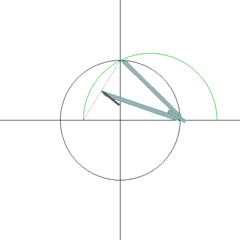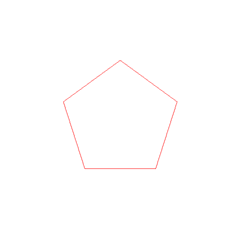
Animated demonstration constructing an inscribed pentagon with compass and straightedge.
How to construct a regular pentagon with only a compass and straightedge.
How to fold a regular pentagon using only a strip of paper
Definition and properties of the pentagon, with interactive animation
Renaissance artists' approximate constructions of regular pentagons Archived 2007-06-25 at the Wayback Machine.
Pentagon. How to calculate various dimensions of regular pentagons.

[Louisiana_State_Univ-1] 1,0 ^1,1 Kalbfleisch, J.D.; Kalbfleisch, J.G.; Stanton, R.G. (1970), «A combinatorial problem on convex regions», Proc. Louisiana Conf. Combinatorics, Graph Theory and Computing, Congressus Numerantium, 1, Baton Rouge, La.: Louisiana State Univ., pp. 180–188

[2] Պենրոուզի սալիկներ

[1]

[2]