Ուղիղ

Վերևից ներքև՝ ուղիղ, կիսաուղիղ (ճառագայթ) և հատված։

Ուղիղ, երկրաչափության հիմնական հասկացություններից մեկն է։ Երբ երկրաչափությունը օգտագործվում է իրական աշխարհը մոդելավորելու համար, ապա գիծը կամ ուղիղը լայնք և բարձրություն չունեցող մարմնի մոդել է ծառայում։ Համարվում է, որ ուղիղն ունի անվերջ մեծ երկարություն։

Ուղղին պատկանող որևէ կետից միայն մի ուղղությամբ շարունակություն ունեցող ուղղի մասը կոչվում է կիսաուղիղ կամ ճառագայթ։ Այդ կետը կոչվում է սկզբնակետ։

Հատված է կոչվում ուղղի այն մասը, որը բաղկացած է նրան պատկանող տրված երկու կետերի միջև գտնվող բոլոր կետերից։ Այդ երկու կետերը կոչվում են հատվածի ծայրեր կամ ծայրակետեր։

Ուղղի երկրաչափական հատկությունները Էվկլիդեսյան երկրաչափությունում

Ցանկացած երկու կետով կարելի է տանել ուղիղ, և այն էլ միայն մեկը։ Երկու տարբեր ուղիներ կամ չեն հատվում, կամ էլ հատվում են միայն մեկ կետում։ Ուղիղը հարթությունը տրոհում է երկու կիսահարթությունների։

Ցանկացած կիսաուղղի վրա սկսած նրա սկզբնակետից կարելի է տեղադրել տրված երկարությամբ հատված, և այն էլ միայն մեկը։

Տրված ուղղի վրա չգտնվող կետով հարթության վրա կարելի է տանել այդ ուղղին զուգահեռ մեկից ոչ ավել ուղիղ։ Ուղղի յուրաքանչյուր կետով կարելի է տանել նրան ուղղահայաց ուղիղ, այն էլ միայն մեկը։

Ուղղի հավասարումը հարթությունում

Երեք տարբեր ուղիղներ։

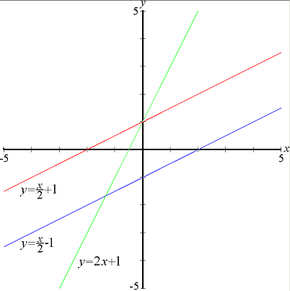
Ուղղի ընդհանուր հանրաշավական հավսարումը դեկարտյան կոորդինատային համակարգում ունի հետևյալ տեսքը՝

$Ax+By+C=0,\,$

որտեղ A, B և C-ն կամայական հաստատուններ են, ընդ որում A և B-ն միաժամանակ հավասար են չեն զրոյի։ Եթե C-ն հավսար է զրոյի, ապա ուղիղը անցնում է կոորդինատների սկզբնակետով։

Ուղղի հավասարման տարբեր ներկայացումներ՝
$y=kx+b,$ կամ $x\cos\theta+y\sin\theta-p=0\,$

Ուղղի հավասարումը անկյունային գործակցով։ Ուղիղը, որը հատում է $Oy$ առանցքը $(0,\;b)$ կետում և կազմում է $\varphi$ $Ox$ առանցքի դրական ուղղության նկատմամբ՝

$y=kx+b,\quad k=\mathrm{tg}\,\varphi.$

$k$ գործակիցը կոչվում է ուղղի անկյունային գործակից։

Ուղղի հավասարումը բևեռային կոորդինատային համակարգում։

$r=\frac{kr\cos\theta+b}{\sin\theta}:$

Այն ներկայացնում են նաև այս տեսքով՝

$r\sin\theta=mr\cos\theta+b.\,$

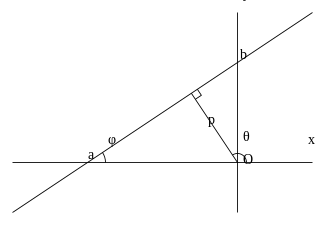
Ուղղի նորմալ հավասարում։

$x\cos\theta+y\sin\theta-p=0,\,$

որտեղ $p$ — կոորդինատների սկզբնակետից ուղղին տարված ուղղահայացի երկարությունն է, իսկ $\theta$ — $Ox$ դրական առանցքի և այդ ուղղահայցի միջև կազմած անկյունն է՝ դրական ուղղությամբ չափելիս։ Եթե $p=0$, ապա ուղիղը անցնում է սկզբնակետով։ Անկյունների միջև գործում է հետևյալ կապը՝

$\theta=\varphi+\frac{\pi}{2}$։

Հետևյալ երկու ուղիղները

$y=k_1x+b_1$,

$y=k_2x+b_2$

իրար զուգահեռ են, եթե նրանց անկյունային գործակիցները հավասար են՝ $k_1=k_2$։

Հետևյալ երկու ուղիղները

$y=k_1x+b_1$,

$y=k_2x+b_2$

մեկը մյուսին ուղղահայաց են, եթե նրանց անկյունային գործակիցների արտադրյալը հավասար է մինուս մեկի՝ $k_1k_2=-1$ և ուղղահայց չեն, եթե արտադրյալը մինուս մեկ չէ։

Երեք $(x_1,\;y_1), (x_2,\;y_2)$ և $(x_3,\;y_3)$ կետերը պատկանում են միևնույն ուղղին այն և միայն այն դեպքում, երբ

$\begin{vmatrix} x_2-x_1 & y_2-y_1 \\ x_3-x_1 & y_3-y_1 \end{vmatrix} = 0$։

$(x_1,\;y_1), (x_2,\;y_2)$ կետերով անցնող ուղղի հավասարումն է

$\begin{vmatrix} x_2-x_1 & y_2-y_1 \\ x-x_1 & y-y_1 \end{vmatrix} = 0$։

կամ էլ պարզեցված տեսքով՝

$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$։

Աղբյուրներ

• Ա․ Վ․ Պոգորելով «Երկրաչափություն», 1988։
• М. Я. Выгодский «Справочник по высшей математики», 1977։