Պրիզմա

 Անվան այլ կիրառումների համար տե՛ս՝ Պրիզմա (այլ կիրառումներ)
Անվան այլ կիրառումների համար տե՛ս՝ Պրիզմա (այլ կիրառումներ)
Պրիզմա (լատին․՝ prisma, հին հունարեն՝ πρίσμα «սղոցվածք» բառից, նաև՝ հատվածակողմ), բազմանիստ։ Պրիզմայի նիստերից երկուսը զուգահեռ հարթություններում ընկած հավասար բազմանկյուններ են, իսկ մյուս բոլոր նիստերը՝ այդ բազմանկյունների հետ ընդհանուր կողմեր ունեցող զուգահեռագծեր։ Այդ երկու հավասար բազմանկյունները կոչվում են պրիզմայի հիմքեր, իսկ մյուս նիստերը, այսինքն՝ զուգահեռագծերը՝ կողմնային նիստեր։ Յուրաքանչյուր կողմնային նիստի երկու հանդիպակաց կողերը գտնվում են հիմքերի վրա, իսկ մյուս երկու կողերը միացնում են հիմքերի գագաթները։ Այդ կողերը կոչվում են կողմնային կողեր։
Պրիզմայի հիմքում ընկած բազմանկյունով էլ որոշվում է նրա տեսակը՝ եռանկյուն, քառանկյուն, հնգանկյուն (պենտապրիզմա) պրիզմա և այլն։
Պրիզման գլանի մասնավոր դեպք է ընդհանուր իմաստով։
Պրիզմաների տեսակներ
[խմբագրել | խմբագրել կոդը]Պրիզման, որի հիմքը զուգահեռագիծ է, կոչվում է զուգահեռանիստ։

Ուղիղ պրիզման այն պրիզման է, որի կողմնային կողերն ուղղահայաց են հիմքի հարթությանը, որտեղից հետևում է, որ նրա կողմնային նիստերն ուղղանկյուններ են[1]։ Մյուս պրիզմաները կոչվում են թեք։ Ուղիղ ուղղանկյուն պրիզման կոչվում նաև ուղղանկյուն զուգահեռանիստ։ Այդպիսի պրիզմայի Շլեֆլի կոդն է՝ { }×{ }×{ }։ Ուղիղ պրիզմայի բարձրությունը հավասար է նրա կողին։
Կանոնավոր պրիզման այն ուղիղ պրիզման է, որի հիմքերը կանոնավոր բազմանկյուններ են։ Կանոնավոր պրիզմայի կողմնային նիստերը հավասար ուղղանկյուններ են։ Կանոնավոր պրիզման, որի կողմնային նիստերը քառակուսիներ են (որոնց բարձրությունը հավասար է հիմքի կողմին) համարվում է կիսականոնավոր բազմանիստ։ Այդպիսի պրիզմայի Շլեֆլի կոդն է՝ t{2,p}:
Կանոնավոր հիմքերով և կողերի նույն երկարությամբ ուղիղ պրիզմաները կազմում են կիսականոնավոր բազմանիստերի երկու անվերջ հաջորդականություններից մեկը, որոնցից երկրորդը կազմում են անտիպրիզմաները։
Հատած պրիզման ոչ զուգահեռ հիմքերով պրիզման է[2]։
Պրիզմայի տարրեր
[խմբագրել | խմբագրել կոդը]| Անվանում | Սահմանում | Գծագրի վրա նշում | Գծագիր |
|---|---|---|---|
| Հիմքեր | Երկու նիստեր, որոնք համընկնող բազմանկյուններ են և ընկած են զուգահեռ հարթություններում։ | , | 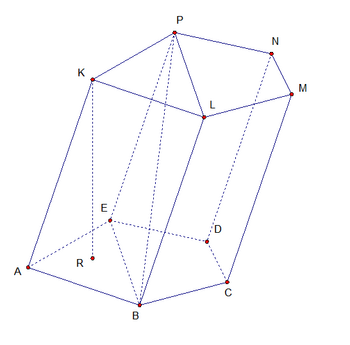 |
| Կողմնային նիստեր | Բոլոր նիստերը, բացի հիմքերից։ Յուրաքանչյուր կողմնային նիստ անպայման զուգահեռանիստ է։ | , , , , | |
| Կողմնային մակերևույթի մակերես | Կողմնային նիստերի մակերևույթների մակերեսների գումարը։ | ||
| Լրիվ մակերևույթի մակերես | Հիմքային և կողմնային նիստերի մակերևույթների մակերեսների գումարը։ | ||
| Կողմնային կողեր | Կողմնային նիստերի ընդհանուր կողմերը։ | , , , , | |
| Բարձրություն | Հատված, որը միացնում է այն հարթությունները, որոնցում ընկած են պրիզմայի հիմքերը, և ուղղահայաց է այդ հարթություններին։ | ||
| Անկյունագիծ | Պրիզմայի՝ նույն նիստին չպատկանող երկու գագաթներ միացնող հատված։ | ||
| Անկյունագծային հարթություն | Հարթություն, որն անցնում է պրիզմայի կողմնային կողով և հիմքի անկյունագծով։ | ||
| Անկյունագծային հատույթ | Պրիզմայի՝ նույն նիստին չպատկանող երկու կողմնային կողերով անցնող հարթությամբ հատույթ, պրիզմայի և անկյունագծային հարթության հատում։ Առաջանում է զուգահեռագիծ, այդ թվում նաև նրա մասնավոր դեպքերը՝ շեղանկյուն, ուղղանկյուն և քառակուսի։ | ||
| Ուղղահայաց հատում | Պրիզմայի և հարթության հատումը, որն ուղղահայաց է նրա կողմնային կողին։ |
Պրիզմայի հատկություններ
[խմբագրել | խմբագրել կոդը]- Պրիզմայի հիմքերը հավասար բազմանկյուններ են։
- Պրիզմայի կողմնային նիստերը զուգահեռագծեր են։
- Պրիզմայի կողմնային կողերը զուգահեռ և հավասար են։
- n-անկյուն պրիզման ունի 3n կող, 2n գագաթ, n+2 նիստ, ընդ որում՝ այդ նիստերից երկուսը նրա հիմքերն են, իսկ n-ը՝ կողմնային նիստերը։
- Պրիզմայի ծավալը հավասար է նրա հիմքի մակերեսի և բարձրության արտադրյալին
- n-անկյուն կանոնավոր հիմքով պրիզմայի ծավալը հավասար է՝
- (որտեղs-ը բազմանկյան կողմի երկարությունն է)։
- Պրիզմայի լրիվ մակերևույթի մակերեսը հավասար է նրա կողմնային մակերևույթի մակերեսի և հիմքի մակերեսի կրկնապատիկի գումարին։
- Կամայական պրիզմայի կողմնային մակերևույթի մակերեսը հավասար է , որտեղ -ն անկյունագծային հատույթի պարագիծն է, -ը՝ կողմնային կողի երկարությունը։
- Ուղիղ պրիզմայի կողմնային մակերևույթի մակերեսը հավասար է նրա հիմքի պարագծի և պրիզմայի բարձրության արտադրյալին, այսինքն՝ , որտեղ -ն հիմքի պարագիծն է, -ը՝ պրիզմայի բարձրությունը։
- Կանոնավոր n-անկյուն հիմքով ուղիղ պրիզմայի կողմնային մակերևույթի մակերեսը հավասար է՝
Կանոնավոր պրիզմայի կողմնային մակերևույտի մակերեսը հավասար է հիմքի պարագիծ անգամ բարձրություն
S կողմնային=Pհիմք x h
- Ուղղահայաց հատույթն ուղղահայաց է պրիզմայի բոլոր կողմնային կողերին։
- Ուղղահայաց հատույթն ուղղահայաց է պրիզմայի բոլոր կողմնային նիստերին։
- Ուղիղ պրիզմայի կրկնակի բազմանիստը երկբուրգն է։
- Կանոնավոր պրիզմայի կողմնային մակերևույտի մակերեսը հավասար է հիմքի պարագիծ անգամ բարձրություն
- Ուղղահայաց հատույթի անկյունները համապատասխան կողմնային կողերին կից երկնիստ անկյունների գծային անկյուններն են։
Ներգծված և արտագծված մարմիններ
[խմբագրել | խմբագրել կոդը]- Պրիզման կոչվում է գնդային մակերևույթին արտագծած, եթե գնդային մակերևույթը շոշափում է նրա բոլոր նիստերը։ Այդ դեպքում գնդային մակերևույթը կոչվում է ներգծված պրիզմային։
- Պրիզման կոչվում է ներգծված գլանին, եթե նրա հիմքերը ներգծված են գլանի հիմքերին։
- Եթե կանոնավոր պրիզմային կարելի է ներգծել գնդային մակերևույթ, ապա գնդային մակերևույթի կենտրոնը բազմանիստի հիմքերի կենտրոնները միացնող հատվածի միջնակետն է։
- Կանոնավոր պրիզմային արտագծած գնդային մակերևույթի կենտրոնը բազմանիստի հիմքերի կենտրոնները միացնող հատվածի միջնակետն է։
Ծանոթագրություններ
[խմբագրել | խմբագրել կոդը]- ↑ Kern, Bland, 1938, էջ 28
- ↑ Kern, Bland, 1938, էջ 81
Գրականություն
[խմբագրել | խմբագրել կոդը]- William F. Kern, James R. Bland ոչ թէ Վիլլիամ, այլ Վիլլիս Ֆ․ Քեռն Solid Mensuration with proofs. — 1938.
- Catherine A. Gorini The facts on file: Geometry handbook. — New York: Infobase Publishing, 2003. — (Facts on file).
- Anthony Pugh Chapter 2: Archimedean polyhedra, prisma and antiprisms // Polyhedra: A visual approach. — California: University of California Press Berkeley, 1976. — ISBN 0-520-03056-7
Արտաքին հղումներ
[խմբագրել | խմբագրել կոդը]- Weisstein, Eric W., "Prism", MathWorld.
- George Olshevsky. «Prismatic polytope». Glossary for Hyperspace.
- Surface Area MATHguide
- Volume MATHguide
- Paper models of prisms and antiprisms
| Ընթերցե՛ք «պրիզմա» բառի բացատրությունը Հայերեն Վիքիբառարանում։ |
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Պրիզմա» հոդվածին։ |
| ||||||
























