Քառակուսային հավասարում
Քառակուսային հավասարում,
- ընդհանուր տեսքի հանրահաշվական հավասարում
որտեղ -ը, անկախ փոփոխական, , , -ն, գործակիցներ, ընդ որում
արտահայտությունը անվանում են քառակուսային եռանդամ[1].
Արմատը, դա փոփոխականի արժեքն է, վերածելով քառակուսային եռանդամը զրոյի, իսկ քառակուսային հավասարումը` ճշմարիտ հավասարության։ Քառակուսային հավասարման տարրերն ունեն հատուկ անվանումներ:[1]։
- -ն կոչվում է առաջին կամ ավագ գործակից,
- -ն կոչվում է երկրորդ, միջին կամ -ի գործակից,
- -ն կոչվում է ազատ անդամ.
Քառակուսային հավասարումը կոչվում է բերված, որում ավագ գործակիցը հավասար է մեկի [1]. Այդպիսի հավասարում կարող ենք ստանալ ամբողջ հավասարումը բաժանելով ավագ գործակցի։
Լրիվ կոչվում է այնպիսի քառակուսային հավասարումը, որի բոլոր գործակիցները տարբեր են 0-ից։
Թերի կոչվում է այնպիսի քառակուսային հավասարումը, որում, բացի ավագ անդամից, գործակիցներից մեկը (կամ երկրորդ գործակիցը, կամ ազատ անդամը), հավասար է 0-ի։
Պատմական տեղեկություններ քառակուսային հավասարման մասին[խմբագրել | խմբագրել կոդը]
Հին Բաբելաոն[խմբագրել | խմբագրել կոդը]
Մեր թվարկությունից առաջ երկրորդ հազարամյակին բաբելոնցիները գիտեին ինչպես լուծել քառակուսային հավասարումը [1]։ Հին Բաբելոնում նրանց լուծումը խիստ կապված էր գործնական խնդիրների հետ, հիմնականում այնպիսին, ինչպես հողատարածքների մակերեսների չափումը, հողային աշխատանքները,ռազմական կարիքների հետ կապված,ընդհանրապես մաթեմատիկայի և աստղագիտության զարգացումով պայմանավորված է այդպիսի գիտելիքների առկայությունը։ Հայտնի է եղել ինչպես լրիվ, այնպես էլ թերի քառակուսային հավասարման լուծման եղանակներ:Բերենք, Հին Բաբելոնում լուծվող քառակուսային հավասարման լուծումների օրինակներ, օգտագործելով ժամանակակից հանրահաշվական գրառումներ։
Քառակուսային հավասարման լուծման կանոնների ժամանակակից շատ անալոգիաներ,բայց բաբելոնյան տեքստերում դատողությունները ֆիքսված չէին,ըստ որի ստացել էին այդ կանոնները։
Հնդկաստան[խմբագրել | խմբագրել կոդը]
Քառակուսային հավասարման օգնությամբ լուծվող խնդիրներ, հանդիպում ենք «Ариабхаттиам» աստղագիտության տրակտում, գրված հնդիկ աստղագետ և մաթեմատիկոս Արիաբխատաի կողմից մեր թվարկության 499 թվականին։ Քառակուսային հավասարման արմատների առաջին հայտնի բանաձևի ընդհանրացումը պատկանում է հնդիկ գիտնական Բրահմագուպտա (մոտ 598 թ.)[1]; Բրահմագուպտան շարադրեց քառակուսային հավասարման լուծման ունիվերսալ կանոնը , բերված կանոնական տեսքի։ ; բացի այս ենթադրվեց, որ գործակիցները, բացի -ից կարող են բացասական լինել։ Գիտնականի ձևակերպված կանոնը իր գոյությամբ համընկնում է այժմյանի հետ։
Քառակուսային հավասարման արմատները իրական թվերի բազմությունում[խմբագրել | խմբագրել կոդը]
I եղանակ Արմատների հաշվման ընդհանուր բանաձևը[խմբագրել | խմբագրել կոդը]
քառակուսային հավասարման արմատները ընդհանուր դեպքում գտնելու համար պետք է օգտվել ներքևում բերված ալգորիթմից։
| Պայման | |||
| Իրական արմատների թիվը | Երկու արմատ | Մեկ արմատ (ինչ որ կոնտեքստում ասում են երկու հավասար արմատների մասին կամ նրա համընկնող արմատների, նաև անվանում են 2-ի բազմապատիկ արմատ) | եզրակացնում են այն մասին, որ իրական թվերի բազմությունում արմատ չկա |
| Բանաձև | Կոմպլեքս արմատների բանաձևը տես ներքևում համապատասխան բաժնում |
Բանաձևը կարելի է ստանալ հետևյալ կերպ
Բազմապատկենք յուրաքանչյուր մասը -ով և ավելացնենք :
Ծանոթություն։ ակնհայտ է, 2-ի բազմապատիկ արմատների համար բանաձևը հանդիսանում է ընդհանուր բանաձևի մասնավոր դեպք, ստացվում է տեղադրելով նրա մեջ D=0 հավասարությունը, իսկ եզրակացությունը իրական արմատների բացակայության մասին, երբ D<0 հետևում է նույնը կատարել, հաշվի առնելով, որ այդ դեպքում -D>0, իսկ .}}
Շարադրված մեթոդը ունիվերսալ է, սակայն ոչ միակը։ Մի հավասարման լուծմանը կարելի է մոտենալ տարբեր եղանակներով, նախապատվությունը ընդհանրապես կախված է հենց լուծվողից։ Բացի դրանից, հաճախ այդ եղանակներից մի քանիսը թվում է բավականաչափ նրբագեղ, պարզ, պակաս աշխատատար, քան ստանդարտը։
II եղանակ. Քառակուսային հավասարման արմատները b զույգ գործակցի դեպքում[խմբագրել | խմբագրել կոդը]
տեսքի հավասարման համար, այսինքն, զույգ -ի դեպքում, որտեղ
(1) բանաձևի փոխարեն, գտնված արմատների համար կարելի է օգտագործել ավելի պարզ արտահայտություն[1].
Ծանոթություն։ վարը տրված բանաձևը կարելի է ստանալ ստանդարտ բանաձևի մեջ տեղադրելով b=2k արտահայտությունը և կատարել այդ դեպքում ոչ բարդ ձևափոխություններ։
| Ոչ բերված | Բերված | D>0 | Ոչ բերված | Բերված |
| հարմար է հաշվել տարբերիչի մեկ չորրորդի արժեքը
Բոլոր անհրաժեշտ հատկություններն այդ դեպքում պահպանվում է . |
. | |||
| D=0 | ||||
III եղանակ. Թերի քառակուսային հավասարման լուծում[խմբագրել | խմբագրել կոդը]
Թերի քառակուսային հավասարման լուծման համար պետք է մոտենալ առանձնակի։ Քննարկենք երեք հնարավոր իրադրություն։
|
|
Եթե , ապա հավասարումը ունի երկու իրական արմատներ , եթե , ապա , իսկ եթե , ապա հավասարումը չունի իրական արմատներ. |
կամ Այդպիսի հավասարումը անպայման ունի երկու իրական արմատներ |
IV եղանակ.Գործակիցների մասնակի հարաբերակցությունների օգտագործում[խմբագրել | խմբագրել կոդը]
Գոյություն ունի քառակուսային հավասարման մասնավոր դեպքեր, որում գործակիցները գտնվում են միմյանց միջև հարաբերակցության մեջ, թույլատրվում է լուծել այն անհամեմատ ավելի պարզ։
Քառակուսային հավասարման արմատներ, որի ավագ գործակցի և ազատ անդամի գումարը հավասար է երկրորդ գործակցին[խմբագրել | խմբագրել կոդը]
Եթե քառակուսային հավասարման առաջին գործակցի և ազատ անդամի գումարը հավասար է երկրորդ գործակցին՝ , ապա նրա արմատ է հանդիսանում և ազատ անդամի հարաբերությունը ավագ անդամին՝ հակադիր նշանով թիվը ().
Եղանակ 1. Սկզբից պարզենք, իրոք այդպիսի հավասարումը ունի արմատ (այդ թվում ,երկու համընկնող)
- .
Այո, դա այդպես է, չէ որ ցանկացած իրական գործակիցների դեպքում , իսկ դա նշանակում է տարբերիչը ոչ բացասական է։ Այսպիսով, եթե , ապա հավասարումը ունի երկու արմատ, իսկ եթե , ապա այն ունի միայն մեկ արմատ։ Գտնենք այդ արմատները։
- .
Մասնավորապես, եթե , ապա կլինի մեկ արմատը՝
Օգտվենք քառակուսային հավասարման երկրաչափական մոդելից, մենք այն կդիտենք ինչպես պարաբոլի աբսցիսների առանցքի հետ հատման կետեր։ Յուրաքանչյուր պարաբոլ անկախ նրա տրված արտահայտությունից հանդիսանում է պատկեր, համաչափ ուղղի նկատմամբ։Դա ցույց է տալիս, որ այդ ուղղին ուղղահայաց յուրաքանչյուր հատված , նրան հատվող պարաբոլը բաժանում է առանցքը համաչափ երկու հավասար մասերի։ Ասվածը, մասնավորապես ճշմարիտ է և աբսցիսների առանցքի համար։ Այսպիսով ցանկացած պարաբոլի համար ճշմարիտ է հետևյալ հավասարություններից մեկը՝ (если ) կամ (եթե ճշմարիտ է հակադիր իմաստով անհավասարությունը։) Օգտագործելով նույնությունը , արտահայտված մոդուլի երկրաչափական իմաստ, նույնպես ընդունելով, որ ( դա կարող ենք ապացուցել, տեղադրելով հավասարությունը քառակուսային եռանդամի մեջ , դրա համար -1 այդ հավասարման արմատն է), անցնենք հաջորդ հավասարության՝ : Եթե հաշվի առնենք, որ տարբերությունը այդ դեպքում, երբ ավելացնում ենք մոդուլը, միշտ դրական է, այն դեպքում, երբ հանում ենք՝ բացասական, որը ասում է այդ դեպքերում նույնությունների մասին և հիշելովէ հավասարության մասին , բացենք մոդուլը : Երկրորդ դեպքում կատարենք անալոգ ձևափոխություններ, հանգում ենք նույն արդյունքի }}
- Այստեղից, նախքան ինչ-որ քառակուսային հավասարում լուծել, հետևում է ստուգել նրա նկատմամբ այդ թեորեմայի հնարավորությունը՝ համեմատել ավագ գործակցի և ազատ անդամի գումարը երկրորդ գործակցի հետ։
Քառակուսային հավասարման արմատներ, որի բոլոր գործակիցների գումարը հավասար է զրոյի[խմբագրել | խմբագրել կոդը]
Եթե քառակուսային հավասարման բոլոր արմատների գումարը հավասար է 0-ի՝(), ապա այդպիսի հավասարման արմատը հանդիսանում է -ը և ազատ անդամի հարաբերությունը ավագ գործակցին՝ ().
Եղանակ 1. Ամենից առաջ նկատենք, որ հավասարությունից հետևում է, որ
Որոշենք արմատների թիվը
գործակիցների ցանկացած արժեքների դեպքում հավասարումը ունի առնվազն մեկ արմատ, իրոք, ցանկացած գործակիցների դեպքում՝ , իսկ նշանակում է և տարբերիչը ոչ բացասական է։ Ուշադրություն դարձրեք, որ եթե , ապա հավասարումը ունի երկու արմատ, եթե , ապա միայն մեկ արմատ։ Գտնենք այդ արմատները.
ինչը և պահանջվում էր ապացուցել։
- մասնավորապես, եթե , ապա հավասարումը ունի միայն մեկ արմատ, որը հանդիսանում է -ը:.
Եղանակ 2. Օգտվենք վերը նշված քառակուսային հավասարման որոշումից, հայտնաբերենք տեղադրման եղանակով, որ 1 թիվը ներկայացնում է այնպիսի դեպք՝ ճշմարիտ հավասարության , հետևաբար միավորը այդպիսի քառակուսային հավասարման արմատն է, Հետո, Վիետի թեորեմի համաձայն գտնենք երկրորդ արմատը, համաձայն այդ թեորեմի հավասարման արմատների արտադրյալը հավասար է թվի՝ հավասար ազատ անդամի առաջին գործակցի հարաբերությանը։- , ч.т.д. }}
- Այսպիսով նախ, ստանդարտ եղանակով հավասարումը լուծելուց առաջ հետևում է ստուգել դրա նկատմամբ այդ թեորեմի կիրառելությունը, գումարել այդ հավասարման բոլոր գործակիցները և տեսնել հավասար է 0-ի այդ գումարը։
V եղանակ. Քառակուսային եռանդամի վերլուծումը գծային արտադրիչների[խմբագրել | խմբագրել կոդը]
Եթե տեսքի եռսնդամը հաջողվում է ինչ-որ կերպով ներկայացնել գծային բազմապատկիչների արտադրյալի, ապա կարելի է գտնել հավասարման արմատները, այն կլինեն և , իրոք, չէ որ , իսկ լուծելով գծային տրված հավասարումները, կստանանք վերը գրվածը։Նշենք, որ քառակուսային եռանդամը միշտ չէ բաշխվում իրական գործակիցներով գծային բազմատկիչների,դա հնարավոր է, եթե նրան համապատասխան հավասարումը ունի իրական արմատներ։
Դիտարկենք մի քանի մասնավոր դեպքեր.
Գումարի (տարբերության) քառակուսու բանաձևի օգտագործումը[խմբագրել | խմբագրել կոդը]
Եթե քառակուսային եռանդամը ունի տեսք, ապա կիրառելով տրված բանաձևը, մենք կարող ենք վերլուծել այն գծային բազմապատկիչների և նշանակում է գտնել արմատները։
Գումարի (տարբերության) լրիվ քառակուսու անջատումը[խմբագրել | խմբագրել կոդը]
Նմանապես տրված բանաձևը կիրառում են, օգտվելով մեթոդից, ստանալով «գումարի (տարբերության) լրիվ քառակուսու անջատումը» անվանումը։ Բերված քառակուսային հավասարման համեմատ ներմուծված նախկին նշանակումներով, դա ցույց է տալիս հետևյալը
- Գումարում և հանում ենք նույն թիվը
. - կիրառվում է բանաձևը ստացված արտահայտությունում, հանելին և ազատ անդամը տեղափոխում են աջ մաս
- աջ և ձախ մասերից դուրս են բերում քառակուսային հավասարման արմատը և արտահայտում է փոփոխականով
Ծանոթություն։ եթե նկատել եք, տրված բանաձևը համընկնում է «Բերված քառակուսային հավասարման արմատները» առաջարկված բաժնի հետ, որը իր հերթին, կարելի է ստանալ (1)ընդհանուր բանաձևից, a=1 հավասարության տեղադրման եղանակով։Այդ փաստը պարզապես համընկում չէ, նկարագրված մեթոդով, դուրս բերելով, ճշմարիտ է մի քանի լրացուցիչ դատողություններ կարելի է բերել ընդհանուր բանաձևով, և նույնպես ապացուցել տարբերիչի հատկությունը։
VI եղանակ. Վիետի ուղիղ և հակադարձ թեորեմի օգտագործումը[խմբագրել | խմբագրել կոդը]
Վիետի ուղիղ թեորեմը (տես ստորև համանուն բաժնում) և նրա հակադարձ թեորեմը թույլ են տալիս բանավոր լուծել բերված քառակուսային հավասարումները, չդիմելով բավարար մեծածավալ բանաձևային հաշվարկումներին (1)։
Համաձայն հակադարձ թեորեմայի, ցանկացած թվերի զույգ (թիվ) ,լինելով ստորև բերված հավասարումների համակարգի լուծումներ, հանդիսանում են հավասարման արմատներ։
Ընտրել բանավոր թվեր, այդ հավասարումներին բավարարելով, կօգնի ուղիղ թեորեմը։Նրա օգնությամբ կարելի է որոշել արմատների նշանները, չիմանալով հենց արմատները։ Դրա համար հետևում է ղեկավարվել կանոններով.
- 1) Եթե ազատ անդամը բացասական է, ապա արմատները ունեն տարբեր նշաններ և մոդուլով ամենամեծ արմատի նշանը՝հ ավասարման երկրորդ գործակցի հակադիր նշանը։
- 2) Եթե ազատ անդամը դրական է, ապա երկու արմատները ունեն միանման նշաններ և այդ նշանը՝ հակադիր է երկրորդ գործակցի նշանին։
VII եղանակ. «Տեղափոխումների» մեթոդ[խմբագրել | խմբագրել կոդը]
Այսպես կոչված «տեղափոխումների» մեթոդը թույլ է տալիս հանգեցել չբերված և չձևափոխված լուծումը ամբողջ գործակիցներով բերված տեսքի այն հավասարման ավագ գործակցին բաժանելու եղանակով՝ ամբողջ գործակիցներով բերվածի լուծման։ Այն եզրափակվում է հետևյալում.
- 1)բազմապատկում ենք երկու մասը արտահայտությամբ
- 2) ներմուծենք նոր փոփոխական y=ax:
- .
Հետո հավասարումը լուծվում է բանավոր վերը նշված եղանակով, հետո վերադառնում ենք տրված ներմուծմանը և գտնում հավասարման արմատները и .
Ենթադրենք, մենք ցանկանում ենք լուծել հավասարումը օգտագործելով Վիետի հակադարձ թեորեմը։Եթե մենք փորձենք նրա երկու մասը 8-ի բաժանենք, ապա կստանանք կոտորակային գործակիցներով բերված տեսքի հավասարում, դրա համար կիրառել թեորեմը, կլինի շատ դժվար։Սակայն օգտվելով տեղափոխումների մեթոդից, մենք կարող ենք ստանալ բերված ամբողջ գործակիցներով։
- .
y=8x բանաձևով կատարենք փոփոխականի փոխարինում, կհանգենք հավասարման.
- .
Ակնհայտ է,որ նրա արմատները կլինեն -4 и 2 թվերը։. Անենք հակադարձ փոխարինումը.
Երկրաչափական իմաստ[խմբագրել | խմբագրել կոդը]
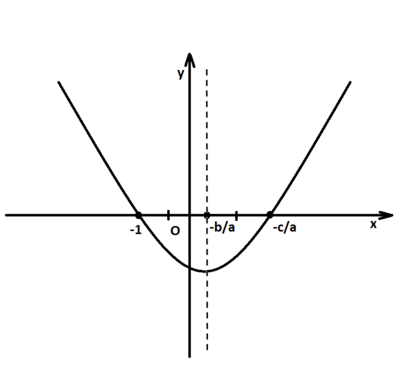
Քառակուսային ֆունկցիայի գրաֆիկը հանդիսանում է պարաբոլ. Քառակուսային հավասարման լուծումներ «արմատներ» անվանում են պարաբոլի աբսցիսների առանցքի հատման կետի աբսցիսը։Եթե քառակուսային ֆունկցիան նկարագրող պարաբոլը, չի հատվում աբսցիսների առանցքի հետ, հավասարումը իրական արմատներ չունի։ Եթե պարաբոլը հատվում է աբսցիսների առանցքի հետ մի կետում (պարաբոլի գագաթում), հավասարումը ունի մեկ իրական արմատ (նույնպես ասում են հավասարումը ունի երկու համընկած արմատներ)։Եթե պարաբոլը հատվում է աբսցիսների առանցքի հետ երկու կետերում, հավասարումը ունի երկու իրական արմատ (տես. պատկերը աջից)։
Եթե գործակիցը դրական է, պարաբոլի ճյուղերը ուղղված են վերև և ընդհակառակը։Եթե գործակիցը դրական է (դրական -ի դեպքում, ընդհակառակը բացասականի դեպքում), ապա պարաբոլի գագաթը գտնվում է ձախ կիսահարթությունում և ընդահակառակը։
Քառակուսային հավասարման լուծման գրաֆիկական եղանակ[խմբագրել | խմբագրել կոդը]
Բացի վերը նկարագրված ունիվերսալ եղանակից, գոյություն ունի այսպես կոչված գրաֆիկական եղանակ։ Ընդհանուր առմամբ այս եղանակը ռացիոնալ տեսքի հավասարման լուծումը կայանում է հետևյալում, միևնույն կոորդինատային հարթությունում կառուցվում է и ֆունկցիաները և գտնում են գրաֆիկների ընդհանուր կետի աբսցիսը, գտնված թիվը և կլինի հավասարման արմատը։
- Կան քառակուսային հավասարման գրաֆիկական լուծման հինգ եղանակներ։
Եղանակ I[խմբագրել | խմբագրել կոդը]
Այդ եղանակով քառակուսային հավասարման լուծման համար կառուցում են ֆունկցիայի գրաֆիկը և գտնում առանցքի հետ հատման կետերի աբսցիսները։
Եղաննակ II[խմբագրել | խմբագրել կոդը]
Այդ եղանակով նույն հավասարման լուծման համար այն ձևափոխում են տեսքի և կառուցում են միևնույն կոորդինատային համակարգում քառակուսային ֆունկցիայի և գծային ֆունկցիայի գրաֆիկները, հետո գտնում են նրանց հատման կետի աբսցիսը։
Եղանակ III[խմբագրել | խմբագրել կոդը]
Այդ եղանակով լուծելու համար տրված հավասարումը նախապես ձևափոխում են տեսքի, օգտվելով գումարի (տարբերության) լրիվ քառակուսու առանձնացման մեթոդից և հետո :Դրանից հետո կառուցվում ֆունկցիայի գրաֆիկը (այն հանդիսանում է ֆունկցիայի գրաֆիկը, տեղաշարժելով միավոր մասշտաբով աջ կամ ձախ կախված նշանից) և ուղղից, զուգահեռ աբսցիսների առանցքին։Հավասարման արմատները կլինեն պարաբոլի և ուղղի հատման կետերի աբսցիսները։
Եղանակ IV[խմբագրել | խմբագրել կոդը]
Քառակուսային հավասարումը ձևափոխվում է տեսքի, կառուցվում է ֆունկցիայի գրաֆիկը (այն ներկայացնում է ֆունկցիայի գրաֆիկը, տեղափոխելով միավոր մասշտաբով վերև, եթե այդ գործակիցը դրական է կամ ներքև, եթե գործակիցը բացասական է ) և , գտնում են նրանց ընդհանուր կետերի աբսցիսները։
Եղանակ V[խմբագրել | խմբագրել կոդը]
Քառակուսային հավասարումը ձևափոխվում է հատուկ տեսքի.
հետո
- .
վերջացնելով ձևափոխությունները կառուցվում է գծային ֆունկցիայի գրաֆիկը և հակադարձ համեմատությամբ -ը, գտնում են այդ ֆունկցիաների հատման կետերի աբսցիսները։ Այդ մեթոդը ունի կիրառելիության սահման, եթե , ապա մեթոդը չեն օգտագործում։
Քառակուսային հավասարումների լուծումը կարկինի և քանոնի օգնությամբ[խմբագրել | խմբագրել կոդը]
Վերը նկարագրված գրաֆիկական մեթոդը ունեն գոյության թերություններ, այն բավականին աշխատատար է, այդ դեպքում կորերի՝ պարաբոլի և հիպերբոլի ճշգրտությամբ կառուցումը անբավարար։ Տրված խնդիրները հատուկ չէ ստորև առաջադրված մեթոդին, ենթադրվում է ավելի ճշգրիտ կառուցումներ կարկնի և քանոնի նկատմամբ։ Որպեսզի կատարենք այդպիսի լուծումը, պետք է կատարել հետևյալ գործողությունների հաջորդականությունը։
- Oxy կոորդինատային համակարգում կառուցել կենտրոնով շրջանագիծ, y առանցքի հետ հատելով C(0;1)կետում։
- Հետո հնարավոր է երեք դեպք.
- շրջանագծի շառավղի երկարությունը գերազանցում է S կետից աբսցիսների առանցքին իջեցված ուղղահայացի երկարությանը։ Այդ դեպքում շրջանագիծը հատվում է x առանցքի հետ երկու կետերում, իսկ հավասարումն ունենում է երկու իրական արմատներ, հավասար այդ կետերի աբսցիսներին։
- շառավիղը հավասար է ուղղահայացին; մեկ կետ և 2-ի բազմապատիկ մեկ իրական արմատ;
- շառավիղը փոքր է ուղղահայացից; բազմությունում արմատներ չկան։
Դիտարկվող եղանակը ենթադրում է շրջանագծի կառուցում, հատվող օրդինատների առանցքին՝ կետերում (կետում), որի աբսցիսները հանդիսանում են լուծվող հավասարման արմատներ։ Ինչպե՞ս կարելի է կառուցել այդպիսի շրջանագիծ։ Ենթադրենք այն կառուցված է։ Շրջանագիծը միարժեքորեն որոշվում է իր տրված երեք կետերով։ Ենթադրենք այն դեպքում, եթե արմատները երկուսն են, դա թող լինի կետերը, որտեղ , բնականաբար, քառակուսային հավասարման իրական արմատները (ընդգծում եմ, եթե նրանք գոյություն ունեն)։ Գտնենք այդպիսի շրջանագծի կենտրոնի կոորդինատները։ Դրա համար ապացուցենք, որ այդ շրջանագիծը անցնում է կետերով։ Իրոք, համաձայն հատողի թեորեմի, ընդունված նշանակումներում տեղի է ունենում հավասարությունը(տես. նկարը)։ Ձևափոխելով այդ արտահայտությունը , ստանում ենք OD հատվածը , որը և որոշում է որոնելի D կետի օրդինատը։ (վերջին ձևափոխություններում օգտագործված է Վիետի թեորեմը (տես, ստորև համանուն բաժնում))։Եթե արմատը մեկն է, ապա աբսցիսների առանցքը այդպիսի շրջանագծի շոշափող է և շրջանագիծը y առանցքի հետ հատվում է 1 կետում, ապա այն անպայման անցնում է նրանից և նշված օրդինատով կետից վերև (մասնավորապես, եթե 1=c/a, դա դեպքում համընկնող կետեր են), որ ապացուցում է հանգունորեն արդեն հատողի և շոշափողի մասին թեորեմի օգտագործումը, հանդիսանալով հատողի մասին թեորեմի մասնավոր դեպք։ Առաջին դեպքում (), որոշվածը կլինի շփման կետ, y առանցքի կետ 1 օրդինատով, և նրա նույն կետը օրդինատով։ Եթե c/a և 1, համընկնող կետեր են, իսկ արմատներն երկուս են, սահմանվածը կլինեն այդ կետերը և հատման կետերը աբսցիսների առանցքի հետ։Այն դեպքում, երբ (1=c/a) և արմատը մեկն է, ընդգծված տեղեկությունը բավարար է ապացուցման համար, որովհետև այդպիսի շրջանագիծը կարող է լինել միակը, նրա կենտրոնը կլինի քառակուսու գագաթը, առաջացած շոշոափողի և ուղղահայացի հատումից, իսկ շառավիղը՝ այդ քառակուսու կողմը կազմված 1:Ենթադրենք շրջանագծի կենտրոնը S-ն է,աբսցիսների առանցքի հետ ունենալով երկու ընդհանուր կետեր։ Գտնենք նրա կոորդինատները, դրա համար այդ կետից իջեցնենք ուղղահայացներ առանցքներին։ Այդ ուղղահայացների ծայրերը կլինեն AB и CD հատվածների միջնակետերը, չէ որ ASB и CSD եռանկյունները հավասարասրուն են, քանի որ AS=BS=CS=DS որպես միևնույն շրջանագծի շառավիղներ, հետևաբար, նրանց բարձրությունները տարված հիմքերին նույնպես հանդիսանում են միջնագծեր։ Գտնենք նշված հատվածների միջնակետերի կոորդինատները։ Քանի որ պարաբոլը համաչափ է ուղղի նկատմամբ,ապա այդ ուղղի կետը նույն աբսցիսով հանդիսանում է AB հատվածի միջնակետ։ Հետևաբար, S կետի աբսցիսը հավասար է այդ թվին։ Այն դեպքում, երբ հավասարումը ունի մեկ արմատ, ապա x առանցքը հանդիսանում է շոշափողային կապ շրջանագծին, դրա համար համաձայն նրա հատկությանը, նրա շառավիղը ուղղահայաց է առանցքներին, հետևաբար և այդ դեպքում նշված թիվը կենտրոնի աբսցիսն է։ Նրա օրդինատը գտնենք այսպես. . Երրորդ հնարավոր դեպքը, երբc\a=1 (և նշանակում է, a=c), ապա :
Քառակուսային հավասարման արմատները կոմպլեքս թվերի բազմությունում[խմբագրել | խմբագրել կոդը]
Իրական գործակիցներով հավասարում[խմբագրել | խմբագրել կոդը]
իրական գործակիցներով քառակուսային հավասարումը ունի ճիշտ երկու կոմպլեքս արմատ, որի մասին ասում է հանրահաշվի հիմնական թեորեմը. Այդ դեպքում, տարբերիչի արժեքից կախված, ինչպես մեկ, այնպես էլ երկու արմատը կարող են չունենալ կեղծ մաս և լինել իրական։
- դեպքում, իրական արմատները երկուսն են և այն որոշվում է հետևյալ բանաձևով
- դեպքում, արմատը մեկն է (որի մասին կարող ենք ասել ինչպես երկու հավասար կամ համընկնող արմատներ), 2-ի բազմապատիկ։
- դեպքում իրական (իրական) արմատ չունի, սակայն գոյություն ունի երկու կոմպլեքս արմատ, արտահայտված նույն բանաձևով, ինչ դրական տարբերիչի դեպքում։ Այդպես նրան կարելի կրկին գրել, արտահայտված արմատ բացասական թվի կեղծ միավորի արտադրյալի տեսքով։
Կոմպլեքս գործակիցներով հավասարում[խմբագրել | խմբագրել կոդը]
Կոմպլեքսի դեպքում՝ քառակուսային հավասարումը լուծվում է նույն (1) բանաձևով և վերը նշված իր տարբերակով, բայց տարբերելիությունը կայանում է միայն երկու դեպքում՝զրոյական տարբերիչ (մեկ կրկնակի արմատ) և ոչ զրոյական՝ (երկու պարզ արմատ)։
Բերված քառակուսային հավասարման արմատներ[խմբագրել | խմբագրել կոդը]
տեսքի քառակուսային հավասարումը, որում ավագ գործակից -ն հավասար է 1-ի, անվանում են բերված:Այս դեպքում արմատների համար (1) բանաձևը պարզեցվում է
Վիետի թեորեմը[խմբագրել | խմբագրել կոդը]
Ձևակերպում[խմբագրել | խմբագրել կոդը]
բերված քառակուսային հավասարման արմատների գումարը հավասար է գործակցին «մինուս» նշանով, իսկ արմատների արտադրյալը հավասար է ազատ անդամին։
Ընդհանուր տեսքի,այսինքն՝ չբերված քառակուսային հավասարման։
Օգտվելով այդ թեորեմից, կարելի է լուծել որոշ չբերված քառակուսային հավասարումներ բանավոր։
}}
Քառակուսային եռանդամի վերլուծումը արտադրիչների և նրանից հետևող թեորեմ[խմբագրել | խմբագրել կոդը]
Եթե հայտնի է քառակուսային եռանդամի երկու արմատները, կարելի է այն վերլուծել հետևյալ բանաձևով
- (2)
Ապացույց[խմբագրել | խմբագրել կոդը]
Այդ պնդման ապացուցման համար օգտվենք Վիետի թեորեմից։Համաձայն այդ թեորեմի и արմատները քառակուսային հավասարումը ծնում համապատասխանություն նրա գործակիցների հետ։ . Տեղադրենք այդ համապատասխանությունը քառակուսի եռանդամի մեջ
- :
Զրոյական տարբերիչի դեպքում լինում է գումարի կամ տարբերության քառակուսու բանաձևի տարբերակներից մեկը։
- (2) բանաձևից ունենք երկու կարևոր հետևություն.
Հետևություն 1[խմբագրել | խմբագրել կոդը]
- Եթե քառակուսային եռանդամը վերլուծվում է իրական գործակիցներով գծային արտադրիչների , ապա նա ունի նույն թվային բազմությանը պատկանող արմատներ:
Ապացույց[խմբագրել | խմբագրել կոդը]
Ենթադրենք :Այդ ժամանակ կրկին գրենք այդ վերլուծությունը, կստանանք,
- .
Համեմատենք ստացված արտահայտությունը (2) բանաձևի հետ, գտնում ենք, որ այդպիսի եռանդամի արմատները հանդիսանում են և : Քանի որ գործակիցները իրական են, ապա և նրանց հակադիր հարաբերությամբ թիվը նույնպես հանդիսանում է բազմության տարր։
Հետևություն 2[խմբագրել | խմբագրել կոդը]
- Եթե քառակուսային եռանդամը չունի իրական գործակիցներով արմատներ, ապա նա չի վերլուծվում իրական գործակիցներով գծային արտադրիչների:
Ապացույց[խմբագրել | խմբագրել կոդը]
Իրոք, եթե մենք ենթադրենք հակառակը (որ այդպիսի եռանդամը վերլուծվում է գծային արտադրիչների), ապա համաձայն հետևություն 1-ի, նա ունի արմատներ բազմությունում,որ հակասում է պայմանին և մեր ենթադրությունը ճշմարիտ չէ և այդպիսի եռանդամը չի վերլուծվում գծային արտադրիչների։

f (x) = x2 − x − 2 = (x + 1)(x − 2) իրական փոփոխական x, x — կետերի կոորդինատներ, որտեղ գրաֆիկը հատվում է x առանցքի հետ, x = −1 и x = 2, հանդիսանում է քառակուսային հավասարման լուծումներ։ x2 − x − 2 = 0.
Քառակուսայինի բերվող հավասարումներ[խմբագրել | խմբագրել կոդը]
Հանրահաշվական[խմբագրել | խմբագրել կոդը]
տեդքի հավասարումը հանդիսանում է քառակուսայինի բերված հավասարում։
Ընդհանուր դեպքում այն լուծվում է տեղադրմամբ, լուծելով վերջին քառակուսային հավասարումը.
Լուծման դեպքում կարելի է վարվել առանց փոխարինման, լուծել երկու հավասարումների համախումբը,
- и
Եթե , ապա հավասարումը ընդունում է տեսքը,
Այդպիսի հավասարումը կոչվում է երկքառակուսի[2][1].
Փոխարինման միջոցով
քառակուսային հավասարումը հանգեցվում է
- հավասարման, հայտնի ինչպես
կրկնվող կամ ընհանրացված-համաչափ հավասարում[1].
Դիֆֆերանցիալ[խմբագրել | խմբագրել կոդը]
Երկրորդ կարգի հաստատուն գործակիցներով համասեռ դիֆֆերենցիալ հավասարումը
տեղադրմամբ հանգեցվում է բնութագրական քառակուսային հավասարման,
Եթե այդ հավասարման լուծումներն են և մեկը մյուսին ոչ հավասար, ապա լուծման ընդհանուր տեսքն է՝
- , որտեղ և , կամայական հաստատուներ են։
Կոմպլեքս արմատների՝ , համար կարելի է գրառել ընդհանուր լուծումը, օգտվելով Էյլերի բանաձևից։
Եթե բնութագրական հավասարման լուծումները համընկնում են , ընդհանուր լուծումը գրառվում է հետևյալ տեսքով
Հաճախ այդպիսի տիպի հավասարումներ հանդիպում է մաթեմատիկայի և ֆիզիկայի ավելի տարաբնույթ խնդիրներում, օրինակ տատանման տեսություն կամ հաստատուն հոսանքի շղթայի տեսություն։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
Գրականություն[խմբագրել | խմբագրել կոդը]
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом / Фестиваль педагогических идей «Открытый урок».
- Калькулятор квадратного уравнения.