Բրահմագուպտայի բանաձև

Էվկլիդեսյան երկրաչափության մեջ Բրահմագուպտայի բանաձևը կապ է հաստատում ներգծյալ քառանկյան կողմերի և մակերեսի միջև։

Բանաձև

Եթե ներգծյալ քառանկյան մակերեսը K է, իսկ կողմերը՝ a, b, c, d, ապա՝

$K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}$

որտեղ s–ը քառանկյան կիսապարագիծն է և հավասար է՝

$s={\frac {a+b+c+d}{2}}.$

Բանաձևը եռանկյան համար Հերոնի բանաձևի ընդհանրացումն է։ Եռանկյունը կարելի է դիտել որպես քառանկյուն, որի կողմերից մեկը հավասար է զրոյի։ Այսպիսով, եթե d կողմը ընդունենք զրո, ապա ներգծյալ քառանկյունը վերածվում է ներգծյալ եռանկյան (քանի որ բոլոր եռանկյուններին հնարավոր է արտագծել շրջանագիծ), իսկ Բրահմագուպտայի բանաձևը՝ Հերոնի բանաձևի պարզեցված ձևն է։

Կիսապարագծից չօգտվելու դեպքում Բրահմագուպտայի բանաձևը կունենա հետևյալ տեսքը՝

$K={\frac {1}{4}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}},$

որը հավասար է

$K={\frac {\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}{4}}$ հավասարմանը։

Ապացույց

Գծանկար ապացույցի համար

Եռանկյունաչափական ապացույց

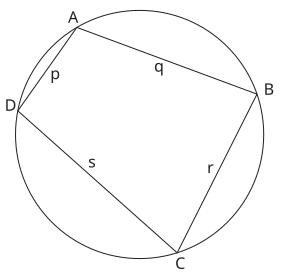
Ներգծյալ քառանկյան K մակերեսը հավասար է △ADB և △BDC եռանկյունների մակերեսների գումարին (գծանկար)․

$={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin C$։

Բայց քանի որ ABCD–ն ներգծյալ քառանկյուն է, ուրմեն ∠DAB = 180° − ∠DCB։ Հետևաբար՝ sin A = sin C։ Այստեղից՝

$K={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin A$

$K^{2}={\frac {1}{4}}(pq+rs)^{2}\sin ^{2}A$

$4K^{2}=(pq+rs)^{2}(1-\cos ^{2}A)=(pq+rs)^{2}-(pq+rs)^{2}\cos ^{2}A.\,$

Կոսինուսների թեորեմի օգնությամբ △ADB և △BDC եռանկյուներից հաշվելով ընդհանուր DB կողը, կստանանք՝

$p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}-2rs\cos C.\,$

Փոխարինելով cos C = −cos A (քանի որ A և C անկյունները հանդիպակաց են) և ձևափոխելով բանաձևը, կստանանք՝

$2(pq+rs)\cos A=p^{2}+q^{2}-r^{2}-s^{2}.\,$

Տեղադրելով սա մակերեսի բանաձևի մեջ՝ կունենանք՝

$4K^{2}=(pq+rs)^{2}-{\frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}$

$16K^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2}.$

Հավասարման աջ կողմը a² − b² = (a − b)(a + b) տեսքի է, ուստի կարելի է ձևափոխել

$[2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2}][2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2}]\,$

որը հավասար է հետևյալ հավասարումներին՝

$=[(r+s)^{2}-(p-q)^{2}][(p+q)^{2}-(r-s)^{2}]\,$

$=(q+r+s-p)(p+r+s-q)(p+q+s-r)(p+q+r-s).\,$

Ներմուծելով S = p + q + r + s2 կիսապարագիծը,

$16K^{2}=16(S-p)(S-q)(S-r)(S-s).\,$

և քառակուսի արմատ հանելով կստանանք՝

$K={\sqrt {(S-p)(S-q)(S-r)(S-s)}}.$

Ոչ-եռանկյունաչափական հավասարում

Բանաձևը կարելի է նաև ապացուցել օգտվելով եռանկյան մակերեսի Հերոնի բանաձից՝ հաշվելով նման երկու եռանկյուները։

Ընդլայնում ոչ ներգծյալ քառանկյունների համար

Ոչ ներգծյալ քառանկյան դեպքում Բրահմագուպտայի բանաձևը կարելի է վերաձևակերպել օգվելով քառանկյան երկու հանդիպակաց անկյուններից.

$K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\theta }}$

որտեղ θ-ն կամայական երկու հանդիպակաց անկյունների կիսագումարն է։ (Անկյունների ընտրությունը էական չէ. եթե ընտրվի մյուս զույգը, ապա դրանց կիսագումարը կլինի 180° − θ։ Քանի որ cos(180° − θ) = −cos θ, ուրեմն՝ cos²(180° − θ) = cos² θ)։ Այս՝ ավելի ընդլայնված բանաձևը, հայտնի է Բրետշնայդերի բանաձև անվամբ։

Ներգծյալ քառանկյան հատկության համաձայն՝ քառանկյան հանդիպակաց անկյունների գումարը հավասար է 180°։ Ուստի, ներգծյալ քառանկյան դեպքում θ–ն 90° է, հետևաբար, Բրետշնայդերի բանաձևը ստանում է Բրահմագուպտայի բանաձևի տեսքը․

$abcd\cos ^{2}\theta =abcd\cos ^{2}\left(90^{\circ }\right)=abcd\cdot 0=0,\,$

Սրանից հետևում է, որ տրված կողմերով քառանկյուններից ամենամեծ մակերեսն ունի ներգծյալ քառանկյունը։

Ցանկացած ուռուցիկ քառանկյան մակերես հավասար է՝

$K={\sqrt {(s-a)(s-b)(s-c)(s-d)-\textstyle {1 \over 4}(ac+bd+pq)(ac+bd-pq)}}\,$

որտեղ p–ն և q–ն քառանկյան անկյունագծերն են։ Ներգծյալ քառանկյան դեպքում, ըստ Պտղոմեոսի թեորեմի, pq = ac + bd և այս բանաձևը վերածվում է Բրահմագուպտայի բանաձևի։

Արտաքին հղումներ

• Weisstein, Eric W. "Brahmagupta's Formula". MathWorld. 

This article incorporates material from proof of Brahmagupta's formula on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.