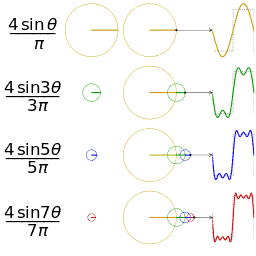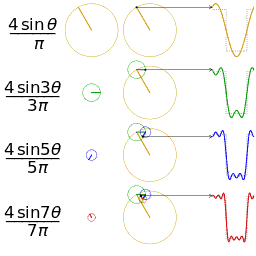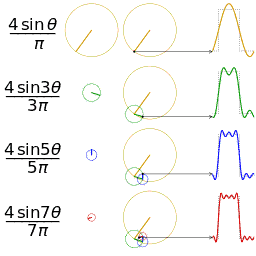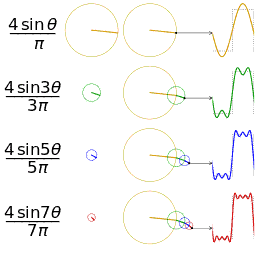Ֆուրիեի շարք
Ֆուրիեի շարք, մաթեմատիկայում պարբերական ֆունկցիայի (որը կարող է լինել որևէ ազդանշան կամ ալիք) վերլուծությունն է ավելի պարզ ֆունկցիաների կամ տատանումների, այն է՝ սինուսոիդների (կամ կոմպսլեքս տեսքով՝ կոմպլեքս էքսպոնենցիալների) վերջավոր կամ անվերջ գումարի տեսքով։ Այդպես է անվանվել ի պատիվ Ֆրանսիացի մաթեմատիկոս Ժոզեֆ Ֆուրիեի, ով առաջինն է ուսումնասիրել այդ շարքերը ջերմահաղորդականության հավասարման կոնտեքստում։ Ֆուրիեյի շարքերի ուսումնասիրությունը Ֆուրիե-անալիզի ճյուղերից է, որն էլ իր հերթին մաս է կազմում Հարմոնիկ անալիզի։ Դեռ խորհրդային տարիներից Հայաստանում մի խումբ մաթեմատիկոսներ, մասնավորապես՝ ակադեմիկոս Ալեքսանդր Թալալյանը և իր ուսանողները, զբաղվում են Ֆուրիեի շարքերի ուսումնասիրությամբ։
Սահմանումը
[խմբագրել | խմբագրել կոդը]Ենթադրենք -ը որևէ ինտեգրելի -պարբերական ֆունկցիա է՝ որոշված ամբողջ իրական թվային առանցքի վրա։ Մենք ցանկանում ենք այն ներկայացնել որպես հետևյալ տեսքի եռանկյունաչափական շարքի գումար.
- ։
Կիրառելով եռանկյունաչափական ֆունկցիաների պարզագույն հատկությունները՝ շարքը կարելի է ձևափոխել և գրել՝
տեսքով։ Սակայն երբեմն նախընտրելի է առավել կոմպակտ
ներկայացումը, որը ստացվում է Ֆուրիեյի շարքից՝ կոմպլեքս էքսպոնենցիալի համար
Եթե -ը եռանկյունաչափական ֆունկցիաների վերջավոր գումար է, ապա կարելի է հեշտորեն համոզվել (օգտվելով եռանկյունաչափական համակարգի օրթոգոնալությունից), որ և գործակիցները որոշվում են հետևյալ բանաձևերով.
- , ,
իսկ կոմպլեքս ներկայացմամբ՝
բանաձևով։
Ընդհանուր դեպքում, տվյալ ինտեգրելի ֆունկցիայի համար կդիտարկենք
եռանկյունաչափական շարքը, որտեղ , և գործակիցները որոշվում են վերը նշված բանաձևերով և այն կանվանենք ֆունկցիայի Ֆուրիեի շարք։
Դասական Ֆուրիե-անալիզն ուսումնասիրում է Ֆուրիեի շարքերի զուգամիտությունը և տարամիտությունը, դրանց պայմանները։
Ներկայացում
[խմբագրել | խմբագրել կոդը]Ֆունկցիայի եռանկյունաչափական շարքով վերլուծությունը հասկանալու համար դիտարկենք
ֆունկցիան, որտեղ ։
Սովորաբար -ով նշվում է ժամանակը, իսկ ֆունկցիան՝ ալիքային տատանումը նկարագրող թվային պարամետրերից որևէ մեկի կախումը ժամանակից։
Վերոնշյալ բանաձևով որոշվող տատանումը կոչվում է հարմոնիկ (ներդաշնակ) տատանում։ Եթե, օրինակ, -ով նկարագրելու լինենք ճոճանակի շեղումը հավասարակշռության դիրքից, ապա այդ կերպ է կտատանվի հավասարակշռության դիրքից շեղված առանց դիմադրության տատանվող ճոճանակը (մաթեմատիկական ճոճանակ)։ Նմանատիպ բանաձևով են որոշվում նաև հավասարաչափ շրջանագծային շարժում կատարող կետի կոորդինատները։
-ն կոչվում է տատանման ամպլիտուդ, -ն՝ հաճախականություն, իսկ -ն՝ փուլ (սկզբնական շեղում)։
Եթե երկու ալիք վերադրվում են, արդյունքում ստացված նոր ալիքի տատանումները նկարագրող թվային գործակիցները սովորաբար հավասար են լինում առանձին ալիքների համապատասխան գործակիցների գումարին (վերադրման սկզբունք, տե՛ս w:Superposition principle)։ Հետևաբար, եթե ունենք տարբեր ներդաշնակ տատանումներ՝
- ,
նրանց վերադրումից առաջացած նոր ալիքի համար կստացվի՝
- ։
Պարզագույն դեպքում, բոլոր -երը որևէ թվի պատիկներ են, ինչը նշանակում է, որ -երը ունեն ընդհանուր պարբերություն։ Մասշտաբը փոխելով՝ առանց ընդհանրությունը խախտելու կարող ենք ենթադրել, որ , այսինքն դիտարկում ենք -պարբերական տատանումները (ընդհանուր դեպքը՝ առանց վերջին ենթադրության, մաթեմատիկայում առանձին ուսումնասիրության առարկա է. տե՛ս w:Almost periodic functions)։ Այդ դեպքում
- ։
Նման վերջավոր գումարի միջոցով կարող ենք ներկայացնել բազմաթիվ -պարբերական տատանումներ, սակայն ոչ բոլորը։ Դա հստակ էր անգամ Ֆուրիեի շարքերի ուսումնասիրության ակունքներում կանգնած մաթեմատիկոսների համար։ Ուստի, հաջորդ բնական քայլը կլիներ փորձել ներկայացնել անվերջ գումարի տեսքով՝
- ։
Սակայն Ֆուրիեյի ժամանակներում ֆունկցիաների անվերջ շարքի գումարը հստակորեն սահմանված չէր. անցավ որոշ ժամանակ, մինչև մաթեմատիկոսներին կհաջողվեր իմաստավորել Ֆուրեի ձևակերպած գաղափարները։ Ֆուրիեի շարքերի ուսումնասիրությունը հետագայում հիմք դարձավ բազմաթիվ նոր մաթեմատիկական տեսությունների և հայտնագործությունների, օրինակ՝ Գեորգ Կանտորի Բազմությունների տեսությունը, որը համարվում է մաթեմատիկայի հիմնարար տեսություներից մեկը։ Բազմությունների տեսությունը ստեղծելի՝ Կանտորը զբաղվում էր Ֆուրիեի շարքերի ուսումնասիրությամբ[1]։
Երկրաչափական մեկնաբանություն
[խմբագրել | խմբագրել կոդը]Նկատենք, որ
վերջավոր գումարին կարելի է տալ հետևյալ երկրաչափական մեկնաբանությունը․ պատկերացնենք՝ ունենք հաջորդական շրջանագծեր, այնպես որ առաջին շրջանագիծն ունի շառավիղ, որի կենտրոնը կոորդինական առանցքի սկզբնակետում է։ Հաջորդ շրջանագիծն ունի շառավիղ, որի կենտրոնը կետում է և այսպես շարունակ (նման նրան, թե ինչպես է Երկիրը պտտվում արեգակի շուրջը, Լուսինն էլ՝ Երկրի)։ Եթե այս շրջանագծերը տեղադրենք «ամեն հաջորդի կենտրոնը մյուսի ընթացիկ կետում» սկզբունքով, ապա վերջին շրջանագծի դիրքին համապատասխանող կետի կոորդինատը պահին կլինի -ն։
-
քառակուսային ալիքի Ֆուրեյի շարքի առաջին չորս ոչ զրոյական անդամներով մոտարկումը
Ընդհանրացումներ
[խմբագրել | խմբագրել կոդը]Ֆուրիեի շարքերը կարելի է սահմանել ցանկացած պարբերական ֆունկցիայի համար՝ փոխելով մասշտաբը։ Երբ պարբերությունը ձգտում է անվերջության, ինքնըստինքյան հանգում ենք Ֆուրիեի ձևափոխությանը։ Վեջինս Ֆուրիեի շարքերի անալոգն է ոչ պարբերական ֆունկցիաների համար։
Ավելի աբստրակտ մոտեցումը հնարավորություն է տալիս Ֆուրիեյի ձևափոխությունները սահմանել Լոկալ կոմպակտ աբելյան խմբերի վրա։ Մաթեմատիկայի՝ նմանատիպ հարցերն ուսումնասիրող բաժինը կոչվում է Աբստրակտ հարմոնիկ անալիզ։ Ավելի ընդհանուր՝ Ֆուրեյի շարքը կարելի դիտարկել Գելֆանդի ձևափոխություն շրջանագծի պտույտների խմբով ծնված խմբային հանրահաշվի վրա։
Ֆուրիեյի ձևափոխությունը հնարավոր է սահմանել նաև գրաֆների և բազմաձևությունների վրա։ Այստեղ մոտեցումը Լապլաս-Բերտրամի օպերատորի սպեկտրալ տեսության միջոցով է՝ ի տարբերություն Աբստրակտ Հարմոնիկ անալիզի առավել հանրահաշվական մոտեցման։
Մեկ այլ ընդհանրացում է եռանկյունաչափական շարքերի փոխարեն այլ ֆունցկիաներ դիտարկելը։ Քսաներորդ դարի երկրորդ կեսում սա ակտիվ բնագավառ էր և կապված էր համակարգերի բազիսության (հետագայում՝ ֆրեյմ) ուսումնասիրության հետ։
Կիրառություններ
[խմբագրել | խմբագրել կոդը]Ժամանակակից տեխնոլոգիաների զարգացումը բազմաթիվ հարցերում պարտական է Ֆուրիեյի հայտնագործությանը։ Այն ժամանակակից ինժեներների ամենկարևոր գործիքներից մեկն է։
Օրինակ, Ռիմանն-Լեբեգի լեմման պնդում է, որ ազդանշանում մեծ հաճախականությունների ներդրումը փոքր է։ Քանի որ մեծ հաճախականությունները պատասխանատու են խզման կետերի համար, նրանց գործակիցները հարմար ձևով ընտրված ֆիլտրերի միջոցով զրոյացնելը հնարավորություն է տալիս մոդիֆիկացնել ֆունկցիան՝ պահպանելով նրա հիմնական մասը և վերացնելով խզման կետերը։ Այս սկզբունքն է ընկած վնասված նկարների կամ ֆայլերի վերակագնման, արխիվացիայի, աղմուկի հեռացման մեթոդների և այլքի հիմքում։ Երբեմն եռանկյունաչափական համակարգի փոխարեն օգտագործվում են այլ համակարգեր, ինչպես օրինակ Վեյվելեթներ, Շիրլեթներ, սակայն հիմնական սկզբունքը նույնն է և հաճախ հանգեցվում է եռանկյունաչափական համակարգով որոշվող հաճախականությունների անալիզին։
Մաթեմատիկայում ևս Ֆուրիեի շարքերն ունեն բազում կիրառություններ, օրինակ՝ մասնակի ածանցյալներով դիֆերենցիալ հավասարումները լուծման գործում և այլն։
Աղբյուրներ
[խմբագրել | խմբագրել կոդը]Գրականություն
[խմբագրել | խմբագրել կոդը]- Grafakos, Loukas (2008), Classical Fourier analysis, Graduate Texts in Mathematics, vol. 249 (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-0-387-09432-8, ISBN 978-0-387-09431-1, MR 2445437
- Grafakos, Loukas (2009), Modern Fourier analysis, Graduate Texts in Mathematics, vol. 250 (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-0-387-09434-2, ISBN 978-0-387-09433-5, MR 2463316
- Zygmund, A. (2002) [1935], Trigonometric series. Vol. I, II, Cambridge Mathematical Library (3rd ed.), Cambridge University Press, ISBN 978-0-521-89053-3, MR 1963498
- Katznelson, Yitzhak (1976). «An introduction to harmonic analysis» (Second corrected ed.). New York: Dover Publications, Inc. ISBN 0-486-63331-4.
{{cite journal}}: Cite journal requires|journal=(օգնություն) - Nina K. Bary, A treatise on trigonometric series, Vols. I, II. Authorized translation by Margaret F. Mullins. A Pergamon Press Book. The Macmillan Co., New York 1964.
- Körner, T.W. (1988), Fourier Analysis, Cambridge University Press, ISBN 0521389917
Արտաքին հղումներ
[խմբագրել | խմբագրել կոդը]- Գրառումներ Ֆուրիեի ձևոփոխության մասին (անգլ.)
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Ֆուրիեի շարք» հոդվածին։ |
| ||||||||||||




































![{\displaystyle f(t)=\operatorname {sgn}[\sin(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf38b4a4145b1eb9ee033ba9fc76962c27d019da)