Ուղղահայացություն

Ուղղահայացություն, երկչափ առնչություն տարբեր օբյեկտների (վեկտորների, ուղիղների, ենթատարածությունների և այլն) միջև:

Ուղղահայացությունը նշանակելու համար գոյություն ունի համընդհանուր նշան՝ $\perp$, որը 1634 թվականին առաջարկել է ֆրանսիացի մաթեմատիկոս Պիեռ Էրիգոնը: Օրինակ, $m$ և $n$ ուղիղների ուղղահայացությունը նշանակվում է այսպես՝ $m\perp n$:

Հարթության վրա

Ուղղահայաց ուղիղները հարթության վրա

Երկու ուղիղներ հարթության վրա կոչվում են ուղղահայաց, եթե հատվելիս առաջացնում են 4 ուղիղ անկյուններ:

$\ell$ ուղղից դուրս գտնվող $P$ կետից $\ell$ ուղղին ուղղահայաց տարված $m$ ուղիղն անվանում են նաև $P$ կետից $\ell$ ուղղին իջեցված ուղղահայաց: Իսկ եթե $P$ կետը գտնվում է $\ell$ ուղղի վրա, ապա ասում են, որ $m$ ուղիղը $P$ կետում $\ell$ ուղղին կանգնեցված ուղղահայացն է:

Կոորդինատներով

Անալիտիկ տեսանկյունից արտահայտած՝

$y=a\cdot x+b$

և

$y=k\cdot x+m$

գծային ֆունկցիաներով տրված ուղիղները կլինեն ուղղահայաց, եթե նրանց անկյունային գործակիցները բավարարեն հետևյալ պայմանը.

$a\cdot k=-1:$

Ուղղահայացի կառուցումը

Ուղղահայացի կառուցում

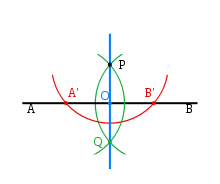
Քայլ 1: Կարկինի միջոցով կառուցենք P կենտրոնով կիսաշրջանագիծ՝ ստանալով А և В կետերը:

Քայլ 2: Չփոփոխելով շառավիղը՝ կառուցենք P կետով անցնող երկու կիսաշրջանագծեր՝ համապատասխանաբար A և В կենտրոններով: Բացի P կետից այդ շրջանագծերը հատվում են ևս մեկ կետում, որը նշանակենք Q:

Քայլ 3: Միացնենք P և Q կետերը: PQ կլինի AB ուղղին տարված ուղղահայաց:

Ուղղին տարված ուղղահայացի հիմքի կոորդինատներ

Դիցուք ուղիղը տրված է $A(x_{a},y_{a})$ և $B(x_{b},y_{b})$ կետերով: $P(x_{p},y_{p})$ կետից ուղղին տարվում է ուղղահայաց: Այդ դեպքում ուղղահայացի $O(x_{o},y_{o})$ հիմքը կարելի է գտնել հետևյալ կերպ․ Եթե $x_{a}=x_{b}$ (ուղղաձիգ), ապա $x_{o}=x_{a}$ և $y_{o}=y_{p}$, Եթե $y_{a}=y_{b}$ (հորիզոնական), ապա $x_{o}=x_{p}$ և $y_{o}=y_{a}$:

Մնացած բոլոր դեպքերում՝

$x_{o}={\frac {x_{a}\cdot (y_{b}-y_{a})^{2}+x_{p}\cdot (x_{b}-x_{a})^{2}+(x_{b}-x_{a})\cdot (y_{b}-y_{a})\cdot (y_{p}-y_{a})}{(y_{b}-y_{a})^{2}+(x_{b}-x_{a})^{2}}}$,

$y_{o}={\frac {(x_{b}-x_{a})\cdot (x_{p}-x_{o})}{(y_{b}-y_{a})}}+y_{p}$:

Եռաչափ տարածության մեջ

Ուղղահայաց ուղիղներ

Երկու ուղիղներ տարածության մեջ ուղղահայաց են միմյանց, եթե նրանք համապատասխանաբար զուգահեռ են երկու այլ՝ միևնույն հարթության մեջ գտնվող փոխուղղահայաց ուղիղների: Միևնույն հարթության մեջ գտնվող երկու ուղիղներ կոչվում են ուղղահայաց (կամ փոխուղղահայաց), եթե կազմում են չորս ուղիղ անկյուններ:

Ուղղի և հարթության ուղղահայացություն

Սահմանում. Ուղիղը կոչվում է հարթությանն ուղղահայաց, եթե այն ուղղահայաց է այդ հարթության մեջ գտնվող բոլոր ուղիղներին (ցանկացած ուղղի):

Հայտանիշ. Եթե ուղիղն ուղղահայաց է հարթության երկու հատվող ուղիղների, ապա այն ուղղահայաց է այդ հարթությանը:

Հարթությունը, որն ուղղահայաց է երկու զուգահեռ ուղիղներից մեկին, ուղղահայաց է նաև մյուսին: Տարածության կամայական կետով անցնում է տրված հարթությանն ուղղահայաց ուղիղ, ընդ որում՝ միայն մեկը:

Ուղղահայաց հարթություններ

Երկու հարթություններ կոչվում են ուղղահայաց, եթե նրանց կազմած երկնիստ անկյունը հավասար է 90°:

• Եթե հարթությունն անցնում է մյուս հարթությանն ուղղահայաց ուղղով, ապա այդ հարթություններն ուղղահայաց են:
• Եթե ուղղահայաց հարթություններից մեկին պատկանող կետից ուղղահայաց տարվի մյուս հարթությանը, ապա այդ ուղղահայացն ամբողջությամբ ընկած կլինի առաջին հարթության մեջ:
• Եթե երկու ուղղահայաց հարթություններից մեկում ուղղահայաց տարվի նրանց հատման գծին, ապա այդ ուղղահայացն ուղղահայաց կլինի երկրորդ հարթությանը:
• Հարթությունը, որն ուղղահայաց է երկու հատվող հարթություններին, ուղղահայաց է նրանց հատման գծին:

Բազմաչափ տարածություններում

Հարթությունների ուղղահայացությունը քառաչափ տարածությունում

Հարթությունների ուղղահայացությունը քառաչափ տարածությունում երկու իմաստ ունի. հարթությունները կարող են ուղղահայաց լինել եռաչափ իմաստով, եթե նրանք հատվում են ուղղով (այսինքն՝ գտնվում են միևնույն հիպերտարածության մեջ), և նրանց կազմած երկնիստ անկյունը հավասար է 90°:

Հարթությունները կարող են ուղղահայաց լինել նաև քառաչափ իմաստով, եթե նրանք հատվում են մի կետում (այսինքն՝ չեն գտնվում միևնույն հիպերտարածության մեջ), և ցանկացած 2 ուղիղներ, որոնք տարված են այդ հարթություններում նրանց հատման կետով (յուրաքանչյուրն իր հարթությունում), ուղղահայաց են:

Քառաչափ տարածության մեջ տրված կետով կարելի է տանել քառաչափ իմաստով փոխուղղահայաց ճիշտ 2 հարթություններ (այդ պատճառով քառաչափ էվկլիդեսյան տարածությունը կարելի է ներկայացնել որպես երկու հարթությունների դեկարտյան արտադրյալ): Իսկ եթե միավորենք ուղղահայացության երկու տեսակներն էլ, ապա տրված կետով կարելի է տանել 6 փոխուղղահայաց հարթություններ (որոնք ուղղահայաց կլինեն վերոնշյալ երկու դեպքերից յուրաքանչյուրում):

Վեց փոխուղղահայաց հարթությունների գոյությունը կարելի է պարզաբանել հետևյալ օրինակով: Դիցուք տրված է x y z t դեկարտյան կոորդինատների համակարգ: Կոորդինատային ուղիղների յուրաքանչյուր զույգի համար գոյություն ունի այդ երկու ուղիղներն ընդգրկող հարթություն: Այդպիսի զույգերի քանակը հավասար է ${\tbinom {4}{2}}=6$: xy, xz, xt, yz, yt, zt, և նրանց համապատասխանում են 6 հարթություններ: Այդ հարթություններից նրանք, որոնք ներառում են նույնանուն առանցք, ուղղահայաց են եռաչափ իմաստով և հատվում են ուղղով (օրինակ, xy և xz, yz և zt), իսկ նրանք, որոնք նույնանուն առանցք չեն ներառում, ուղահայաց են քառաչափ իմաստով և հատվում են կետով (օրինակ, xy և zt, yz և xt):

Հիպերտարածության և ուղղի ուղղահայացություն

Դիցուք տրված է n-աչափ $\mathbb {R} ^{n}$(n>2) էվկլիդեսյան տարածություն և նրա հետ զուգակցված $W^{n}$ վեկտորական տարածություն, իսկ l ուղիղը $L^{1}$ ուղղորդված վեկտորական տարածության հետ և $\Pi _{k}$ հիպերտարածությունը $L^{k}$ ուղղորդված վեկտորական տարածության հետ (որտեղ $L_{1}\subset W^{n}$, $L^{k}\subset W^{n},\ k<n$) պատկանում են $\mathbb {R} ^{n}$ տարածությանը:

l ուղիղը կոչվում է $\Pi _{k}$ հիպերտարածությանն ուղղահայաց, եթե $L_{1}$ ենթատարածությունը օրթոգոնալ է $L^{k}$ ենթատարածությանը, այսինքն՝ $(\forall {\vec {a}}\in L_{1})\ (\forall {\vec {b}}\in L_{k})\ {\vec {a}}{\vec {b}}=0$:

Տարբերակներ և ընդհանրացումներ

• Ինվերսիայի տեսությունում ներմուծվում են շրջանագիծ կամ ուղիղ՝ ուղղահայաց $\Gamma$ շրջանագծին:
• Շրջանագծերի և ինվերսիայի տեսությունում երկու շրջանագծեր, որոնք հատվում են ուղիղ անկյան տակ, կոչվում են օրթոգոնալ (ուղղահայաց): Շրջանագծերը կարելի է համարել օրթոգոնալ, եթե նրանք միմյանց հետ կազմում են ուղիղ ակյուն: Սովորաբար կորերի կազմած անկյունը նրանց՝ հատման կետում տարված շոշափողների կազմած անկյունն է:
• Ինվերսիայի տեսությունում ուղիղն ուղղահայաց է $\Gamma$ շրջանագծին, եթե անցնում է վերջինիս կենտրոնով:

Տես նաև

• Նորմալ
• Զուգահեռություն
• Ուղղանկյունություն