Ինքնակամ ճառագայթում
Ինքնակամ ճառագայթում, կամ ինքնաբերական ճառագայթում քվանտային համակարգերի (ատոմներ, մոլեկուլներ) կողմից ինքնակամ էլեկտրամագնիսական ճառագայթման երևույթ։ Այն տեղի է ունենում երբ համակարգը գրգռված վիճակից անցնում է ստացիոնար վիճակ։ Եթե ատոմը E2 մակարդակում է, այն չի կարող ֆոտոն կլանել, բայց կարող է ինքնակամորեն վերադառնալ E1 մակարդակ։
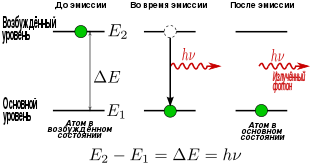
Ինքնակամ ճառագայթումը մի գործընթաց է, որտեղ քվանտային-մեխանիկական համակարգը (օրինակ, մոլեկուլ, ատոմ կամ այլ մասնիկ) անցնում է գրգռված էներգետիկ վիճակից ավելի ցածր էներգետիկ վիճակի (օրինակ՝ հիմնական վիճակ) և արտանետում է ֆոտոնի տեսքով՝ քվանտային էներգիայի քանակություն։ Այս գործընթացը կոչվում է քվանտային ճառագայթում։ Ինքնակամ ճառագայթումը, ի վերջո, պատասխանատու է լույսի մեծ մասի համար, որը մենք տեսնում ենք մեր շուրջը։ Այն այնքան համատարած է, որ կան բազմաթիվ անուններ կրող երևույթներ, որոնք, ըստ էության, նույն գործընթացն են։ Եթե ատոմները (կամ մոլեկուլները), որոնք հարուցվել են որևէ այլ կերպ, քան ջեռուցման, ինքնաբուխ ճառագայթման կոչվում է լումիսիսցենցիա։ Երբեմն մոլեկուլները մետա-կայուն մակարդակ ունեն և շարունակում են լուսարձակող ճառագայթումը անջատելուց հետո երկար ժամանակ։ Սա կոչվում է ֆոսֆորեսցենզիա։ Մարմինները, որոնք խավարում լուսարձակում են, ֆոսֆորեսծում են։ Լազերները սկսում են ինքնաբուխ ճառագայթումից, իսկ հետո շարունակական աշխատանքի ընթացքում աշխատում են խթանված ճառագայթման միջոցով։
Ինքնակամ ճառագայթումը չի կարող բացատրվել դասական էլեկտրամագնիսական տեսությամբ և իր էությամբ քվանտային գործընթաց է։ Առաջին մարդը, ով հենց ինքնաբուխ ճառագայթման արագությունը դուրս բերեց առաջին սկզբունքներից, Դիրակն էր իր քվանտային ճառագայթման տեսության մեջ, տեսություն, որը նա հետագայում անվանեց Քվանտային էլեկտրադինամիկա։ Ժամանակակից ֆիզիկոսները, երբ նրանք խնդրել են ֆիզիկական բացատրություն տալ ինքնակամ ճառագայթմանը, սովորաբար վերաբերում են էլեկտրամագնիսական դաշտի զրոյական էներգիային։ 1963 թվականին մշակվել է Ջեյնս–Կամմինգսի մոդելը, որը նկարագրում է երկմակարդակ ատոմի համակարգը, որը փոխազդում է քվանտային դաշտային մոդայի (այսինքն վակուումային) հետ օպտիկական ռեզոնատորի մեջ։ Այն տվել է ոչ ինտուիտիվ կանխատեսում, որ ինքնակամ ճառագայթման արագությունը կարող է ճշգրտվել՝ կախված շրջակա վակուումային դաշտի սահմանային պայմաններից։
Ալբերտ Այնշթայնի ֆենոմենատրամաբանական սահմանում[խմբագրել | խմբագրել կոդը]
Ինքնակամ ճառագայթման հաճախությունը որոշվում է 1 և 2 մակարդակների էներգիաների տարբերությունով․
Եթե մակարդակի ատոմային «բնակելիությունը» հավասար է , ապա ինքնակամ ճառագայթման հզորությունը հավասար է․
որտեղ -ը 2-րդ մակարդակից 1-ին անցնելու հավանականությունն է․
Ինքնակամ ժառագայթման լրիվ հավանականությունը հավասար է․
Օսցիլիատորի ուժը հավասար է․
Ինքնակամ ճառագայթման արագության հաստատունություն[խմբագրել | խմբագրել կոդը]
Այնշթայնի կողմից ֆենոմենատրամաբանական ներդրված ինքնակամ ճառագայթման արագությունը երկար ժամանակ համարվում էր ատոմների (մոլեկուլների) ներքին անբաժանելի հատկությունը։ Շրջապատի հետ ջերմադինամիկ հավասարակշռությունը ժամանակ այս հատկության կարևորագույն նշաններից մեկը իր անշրջելիությունն է։ Այս հատկությունը պայմանավորված է ատոմի (մոլեկուլի) կողմից անսահման թվով վակուումային մոդերի հետ փոխազդեցությամբ։ Դրանց քանակի փոփոխությանը հանգեցնում է ճառագայթման արագության փոփոխությանը։ Դրա հասնելու համար կարելի է ատոմը տեղադրել ռեզոնատորի մեջ[1]։
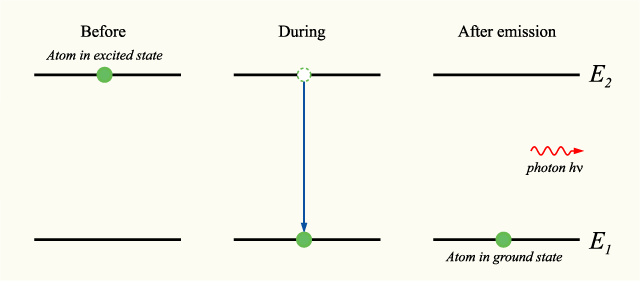 Ուսումնասիրենք միաէլեկտրոն ատոմ, որը ունի երկու էներգետիկ մակարդակ և , որոնք իրարից տարբերվում են -ով։
Ուսումնասիրենք միաէլեկտրոն ատոմ, որը ունի երկու էներգետիկ մակարդակ և , որոնք իրարից տարբերվում են -ով։
Ֆոտոնի ճառագայթման հավանականությունը հայտնի է որպես - Այնշթայնի գործակից և հավասար է․
որտեղ միավոր հաճախության մեջ մոդերի քանակն է՝ մոդերի խտությունը։.
Գրգռված վիճակից ժամանակ հետո մակարդակում գրգռված ատոմ գտնելու հավանականությունը հավասար է .
Ինքնակամ ճառագայթման պատճառ[խմբագրել | խմբագրել կոդը]
Ինքնակամ ճառագայթման գործընթացը հնարավոր չէ բացատրել քվանտային մեխանիկայի նախնական տարբերակի տեսանկյունից, որտեղ տեղի է ունեցել ատոմի էներգիայի մակարդակների քվանտավորում, սակայն չի եղել էլեկտրամագնիսական դաշտի քվանտավորում։ Գրգռված ատոմների վիճակը իրենից ներկայացնում է Շրյոդինգերի հավասարման ճշգրիտ ստացիոնար լուծումները։ Այսպիսով, ատոմների անսահման երկար պետք է մնան գրգռված վիճակում։ Ինքնակամ ճառագայթման պատճառը ատոմի հետ զրոյական տատանումներ ունեցող էլեկտրամագնիսական դաշտի փոխազդեցության է։ Ատոմի վիճակը դադարում է կայուն լինել առաքվող քվանտի հաճախականության հավասար հաճախականությամբ զրոյական տատանումների բաղադրիչի ազդեցության հետևանքով[2]։
Տես նաև[խմբագրել | խմբագրել կոդը]
Ծանոթագրություն[խմբագրել | խմբագրել կոդը]
- ↑ Serge, KLleppner, 1989
- ↑ Мигдал, Аркадий Бейнусович, В. П. Крайнов Глава 1. Размерные и модельные оценки. 4. Оценки в квантовой электродинамике. Нулевые колебания электромагнитного поля // Приближенные методы квантовой механики. — Москва: Наука, 1966. — С. 47—50.
Գրականություն[խմբագրել | խմբագրել կոդը]
- Serge Haroche and Daniel KLleppner Cavity Quantum Electrodynamics. — Physics Today, 1989. — С. 24.
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 4, էջ 366)։ |

















