Պարաբոլ
| Այս հոդվածն աղբյուրների կարիք ունի։ Դուք կարող եք բարելավել հոդվածը՝ գտնելով բերված տեղեկությունների հաստատումը վստահելի աղբյուրներում և ավելացնելով դրանց հղումները հոդվածին։ Անհիմն հղումները ենթակա են հեռացման։ |
Պարաբոլը (հունարեն παραβολή՝ ավելացում բառից), հարթ կոր է, ունի համաչափության առանցք։
Պարաբոլի սահմանումներն են՝
- Պարաբոլը կոորդինատային հարթության այն կետերի բազմությունն է, որոնք հավասարահեռ են առանցքից եւ կիզակետից։
- Պարաբոլը կոնական հատույթներից այն մեկն է, որն ստացվում է կոնի մակերևույթը նրա ծնիչին զուգահեռ հարթությունով հատելիս։
- Պարաբոլը քառակուսի եռանդամ ֆունկցիայի գրաֆիկն է։
Պարաբոլը որպես քառակուսի եռանդամի գրաֆիկ[խմբագրել | խմբագրել կոդը]

Պարաբոլ կոչվում է քառակուսային եռանդամի գրաֆիկը։
Այս դեպքում պարաբոլի գագաթ է հանդիսանում կետը։
Մասնավորապես, դեպքում (1)
պարաբոլի գագաթը գտնվում է կոորդինատների սկզբնակետում։
Անցնենք կոորդինատային նոր համակարգի, փոխելով կոորդինատային առանցքների անունները՝ այսինքն օրդինատների առանցքը նախկին աբսցիսների առանցքն է, իսկ աբսցիսների առանցքը՝ նախկին օրդինատնեռի առանցքը։ Այս նոր համակարգում (1)-ը կգրվի տեսքով, կամ նշանակելով -ն 2p-ով՝ (համարենք, որ a > 0)
տեսքով։ (2)-ը կոչվում է պարաբոլի կանոնական հավասարում նշված կոորդինատային համակարգում։ Պարզենք p գործակցի երկրաչափական իմաստը։ Դիտարկենք կետը, որը կոչվում է պարաբոլի ֆոկուս և հավասարումով որոշվող d ուղիղը, որը կոչվում է պարաբոլի դիրեկտրիս։ Դիցուք M(x;y)-ը պարաբոլի կամայական կետ է։ (2) հավասարումից հետևում է, որ x ≥ 0: Ուստի M կետի հեռավորությունը d դիրեկտրիսից կլինի δ = +x, իսկ և քանի որ , ապա MF=δ: Ուստի, պարաբոլի բոլոր կետերը հավասարահեռ են նրա ֆոկուսից և դիրեկտրիսից։ Այսպիսով, պարաբոլի երկրաչափական սահմանումը հետևյալն է՝
- Պարաբոլ կոչվում է հարթոււթյան այն կետերի երկրաչափական տեղը, որոնք հավասարահեռ են տված կետից և տված ուղղից[1]։
Պարաբոլի երկրաչափական տեսքը[խմբագրել | խմբագրել կոդը]

Պարաբոլի բոլոր կետերը գտնվում են հավասար հեռավորության վրա այն ուղղից, որը համարվում է առանցք եւ այն կետից, որը համարվում է կիզակետ։
Պարաբոլը բնության մեջ[խմբագրել | խմբագրել կոդը]
Բնության մեջ պարաբոլը հանդիպում է տարբեր իրավիճակներում։ Պարաբոլի տեսք ունեն երկնային մարմինների ուղեծրերը, որոնք պտտվում են ավելի մեծ մարմնի ստեղծած գրավիտացիոն դաշտում։
Որոշակի անկյան տակ դեպի վեր նետված ֆիզիկական մարմինների, օրինակ՝ գնդակի հետագիծը նույնպես ունի պարաբոլի տեսք։ Այդպիսի հետագիծ ունի նաեւ շատրվանի ջրի շիթը։
Կիրառությունը[խմբագրել | խմբագրել կոդը]
Առանցքին զուգահեռ ճառագայթների փունջը կիզակետում հավաքելու պարաբոլի հատկությունը կիրառվում է լուսարձակների, լապտերների, ինչպես նաեւ արբանյակային ալեհավաքների եւ արեւային մարտկոցների կառուցվածքներում եւ այլ բնագավառներում։
Պարաբոլը որպես կոնական հատույթ[խմբագրել | խմբագրել կոդը]
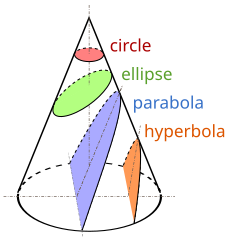
Պարաբոլը ստացվում է այն դեպքում, երբ կոնի մակերեւույթը հատում ենք նրա ծնիչին զուգահեռ հարթությամբ։
Պարաբոլը կոնական հատույթների երկու բաց կորերից մեկն է։ Մյուսը հիպերբոլն է։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Պրիվալով, Ի․. Անալիտիկ երկրաչափություն. Արխիվացված է օրիգինալից 2021 թ․ օգոստոսի 13-ին. Վերցված է 2021 թ․ օգոստոսի 20-ին.











