Սեղան (երկրաչափություն)
| Այս հոդվածն աղբյուրների կարիք ունի։ Դուք կարող եք բարելավել հոդվածը՝ գտնելով բերված տեղեկությունների հաստատումը վստահելի աղբյուրներում և ավելացնելով դրանց հղումները հոդվածին։ Անհիմն հղումները ենթակա են հեռացման։ |
 Անվան այլ կիրառումների համար տե՛ս՝ Սեղան (այլ կիրառումներ)
Անվան այլ կիրառումների համար տե՛ս՝ Սեղան (այլ կիրառումներ)

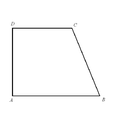
Սեղան է կոչվում այն քառանկյունը, որի երկու հանդիպակաց կողմերը զուգահեռ են միմյանց, իսկ մյուս երկուսը՝ ոչ։
Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր։ (Օրինակ՝ նկարում AB-ն սեղանի փոքր հիմքն է, DC-ն՝ մեծ հիմքը)
Սեղանի ոչ զուգահեռ կողմերը կոչվում են սրունքներ։ (Օրինակ՝ նկարում AD-ն, BC-ն)
Սեղանները կարող են լինել հավասարասրուն և ուղղանկյուն։ Հավասարասրուն սեղան է կոչվում այն սեղանը, որի սրունքները (կողմնային կողերը) հավասար են միմյանց։ Իսկ ուղղանկյուն սեղան է կոչվում այն սեղանը, որի սրունքներից մեկը ուղղահայաց է հիմքերին[1][2]։
Սեղանի տարրերի սահմանումներ[խմբագրել | խմբագրել կոդը]
Սեղանի տարրեր[խմբագրել | խմբագրել կոդը]

- Զուգահեռ կողմերը կոչվում են հիմքեր․
- 2 մյուս կողմերը կոչվում են սրունքներ.
- Սրունքների միջնակետերը միացնող գիծը կոչվում է սեղանի միջին գիծ.
Սեղանների տեսակները[խմբագրել | խմբագրել կոդը]
- Այն սեղանները, որոնց սրունքները հավասար են կոչվում են հավասարասրուն[3][4] սեղաններ։
- Այն սեղանը, որն ունի ուղիղ անկյուն, կոչվում է ուղղանկյուն սեղան։
-
Հավասարասրուն սեղան
-
Ուղղանկյուն սեղան
Ընդհանուր հատկություններ[խմբագրել | խմբագրել կոդը]
- Սեղանի բարձրությունը
- որտեղ — մեծ հիմքն է, — փոքր հիմքն է, и — սրունքներ.
- և անկյունագծերը, և կողմերը կապված են
- արտահայտությամբ։
- Անկյունագծերը արտահայտվում են՝
- Եվ ընդհակառակը՝
- Եթե հայտնի է բարձրությունը,ապա
Ներգծված և արտագծված շրջանագծեր[խմբագրել | խմբագրել կոդը]
- Արտագծված շրջանագծի շառավիղը՝
- որտեղ — սրունք, — մեծ հիմք, — փոքր հիմք, — հավասարասրուն սեղանի անկյունագծերը
- Եթե , ապա հավասարասրուն սեղանին կարելի է ներգծել,
- շառավղով շրջանագիծ։
Սեղանի մակերեսը[խմբագրել | խմբագրել կոդը]
- և սեղանի հիմքերի և — բարձրության միջոցով՝
- միջին գծի և բարձրության միջոցով՝
- միջին գիծը հավասար է հիմքերի կիսագումարին՝
- սեղանի մակերեսը , հիմքերի և և ոչ զուգահեռ կողմերի միջոցով՝
- հավասարասրուն սեղանի մակերեսը ներգծված շրջանագծի շառավիղի և հիմքին կից անկյան միջոցով՝
- մասնավորապես, եթե տվյալ անկյունը 30° է, ապա
- հավասարասրուն սեղանի մակերեսը կողմի և մեծ հիմքին կից անկյան միջացով։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Wolfram MathWorld
- ↑ «Вся элементарная математика». Արխիվացված է օրիգինալից 2015 թ․ հուլիսի 9-ին. Վերցված է 2018 թ․ օգոստոսի 12-ին.
- ↑ Коллектив авторов Современный справочник школьника. 5-11 классы. Все предметы. — Litres, 2015-09-03. — С. 82. — 482 с. — ISBN 9785457410022
- ↑ М. И. Сканави Элементарная математика. — 2013. — С. 437. — 611 с. — ISBN 9785458254489