Խորանարդ ֆունկցիա

Խորանարդ ֆունկցիայի գրաֆիկը (խորանարդ պարաբոլ)

Խորանարդ ֆունկցիան մաթեմատիկայում դա $f:\mathbb {R} \to \mathbb {R}$ տեսքի թվային ֆունկցիան է

$f(x)=ax^{3}+bx^{2}+cx+d,\quad x\in \mathbb {R} ,$

որտեղ $a\neq 0.$ Այլ կերպ ասած՝ խորանարդ ֆունկցիան երրորդ աստիճանի բազմանդամ է։

Անալիտիկ հատկությունները

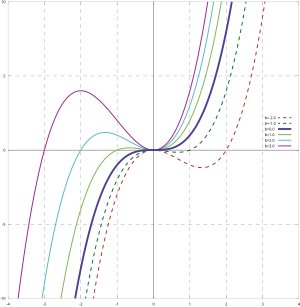
$f(x)=ax^{3}+bx^{2}+cx+d$ ֆունկցիայի ածանցյալը ունի $f'(x)=3ax^{2}+2bx+c$ տեսքը։ Այն դեպքում, երբ $f'(x)=0$ քառակաուսային հավասարման դիսկրիմինանտը (տարբերիչը)՝ ${\frac {D}{4}}=b^{2}-3ac$ մեծ է 0-ից, այն ունի երկու տարբեր արմատներ, որոնք հանդիսանում են $f$ ֆունկցիայի կրիտիկական կետերը։ Ընդ որում․ նրանցից մեկը հանդիսանում է լոկալ մաքսիմումի, իսկ մյուսը՝ լոկալ մինինումի կետ։

Գրաֆիկը

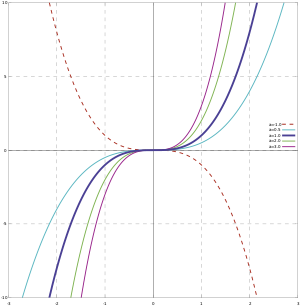
Խորանարդ ֆունկցիայի գրաֆիկը կոչվում է խորանարդ պարաբոլ։ Գրականության մեջ հաճախ հանդիպում են ֆունկցիայի սահմանումները $y=ax^{3}$ կամ $y=x^{3}$ տեսքով։ Հեշտ է նկատել, որ զուգահեռ տեղափոխմամբ խորանարդ պարաբոլը կարելի է բերել այն տեսքին, երբ այն տրված է $y=ax^{3}-px$ հավասարումով։ Հարթության աֆինական ձևափոխության միջոցով կարելի է հասնել այն բանին, որ $a=1$ և $p=0$։

Բացի այդ, խորանարդ պարաբոլը

• համաչափ ՝ թեքման կետի նկատմամբ,
• միշտ հատում է աբցիսների առանցքը, գոնե մեկ կետում,
• չունի ընդհանուր կետ թեքման կետում տարված շոշափողի հետ՝ բացի շոշափման կետից։

Ֆունկցիայի վարքը գործակցի փոփոխության դեպքում

Գործակիցը խորանարդի դեպքում	Գործակիցը քառակուսու դեպքում	Գործակիցը առաջին աստիճանի դեպքում

Կոլինեարությունը

Խորանարդ ֆունկցիայի գրաֆիկի կոլինեար կետերում տարված շոշոփողները գրաֆիկը հատում են նորից կոլինեար կետերում։

Գրականություն

• Л. С. Понтрягин, Кубическая парабола // «Квант», 1984, № 3։
• Ի․Ն․ Բրոնշտեյն, Կ․ Ա․ Սեմենդյաև, «Մաթեմատիկայի խնդրագիրք», «Наука», М. 1967, էջ 84։