Շելլի տեսակավորում

Շելլի տեսակավորում
Տեսակ	տեսակավորման ալգորիթմ, in-place algorithm? և համեմատություններով դասակարգում
Դաս	տեսակավորման ալգորիթմ
Տվյալների կառուցվածք	$O(1)$
Վատագույն դեպքում կատարումը	$O(n^{2})$
Լավագույն դեպքում կատարումը	$O(n\log n)$
Օգտագործում է	զանգված
Հայտնաբերող	Donald Shell?

Շելլի տեսակավորում ալգորիթմ գունավոր բարեր

Շելլի տեսակավորումը (անգլ.՝ Shell sort) — տեսակավորման ալգորիթմ, հանդիսանում է ներդրմամբ տեսակավորման կատարելագործված տեսակը։ Շելլի մեթոդի գաղափարն այն է, որ իրար հետ կարող են համեմատվել ոչ միայն կողք կողքի գտնվող տարրեը, այլ նաև նրանք, որոնք գտնվում են իրարից որոշակի հեռավորության վրա։ Այլ կերպ ասած դա հենց ներդրմամբ տեսակավորումն է՝նախնական «կոպիտ» անցումներով։ Պղպջակային տեսակավորման անալոգային մեթոդը կոչվում է սանրային տեսակավորում։

Նկարագրություն

Շելլի տեսակավորման ժամանակ իրար հետ համեմատվում և տեսակավորվում են այն արժեքները, որոնք գտնվում են իրարից որոշակի $d$ հեռավորության վրա (տես.ներքևում)։ Դրանից հետո այդ գործընթացը կրկնվում է $d$-ի ավելի փոքր արժեքների համար, իսկ տեսակավորումն ավարտվում է, երբ $d=1$ (այսինքն սովորական ներդրմամբ տեսակավորում)։ Շելլի տեսակավորման էֆֆեկտիվությունը որոշ դեպքերում այն է, որ տարրերը ավելի արագ են դասավորվում իրենց տեղերում (տեսակավորման հասարակ մեթոդների ժամանակ, օրինակ պղպջակային, երկու էլեմենտի յուրաքանչյուր տեղաշարժը փոքրացնում է ինվերսիաների քանակը ցանկում առավելագույնը 1-ով, իսկ Շելլի տեսակավորման ժամանակ այդ թիվը կարող է ավելի շատ լինել)։

Չնայած նրան, որ Շելլի տեսակավորումը շատ դեպքերում ավելի դանդաղ է, քան արագ տեսակավորումը, այն ունի որոշակի առավելություններ.

• Պահանջարկի բացակայությունը հիշողության գրապահոցում,
• դեգրադացիայի բացակայությունը տվյալների անհաջող հավաքածուի դեպքում — արագ տեսակավորումը հեշտ դեգրադացվում է մինչև O(n²), որն ավելի վատ է, քան Շելլի տեսակավորման համար ապահովագրած ամենավատ ժամանակը։

Պատմություն

Շելլի տեսակավորումը անվանլելի է նրա հեղինակի — Դոնալդ Շելլի պատվին, որը հրապարակել է այս ալգորիթմը 1959 թ-ին։ Որոշ երկրներում այս ալգորիթմը անվանում են Շելլ-Մեցների ալգորիթմ Մառլեն Մենցեր-Նորտոնի պատվին։ Սակայն հետագայում Մենցերը հերքել է դա՝ ասելով. «Ես ոչ մի առնչություն չունեմ այդ տեսակավորման հետ, և իմ անունը երբեք չպետք է կապվի դրա հետ»։

Օրինակ

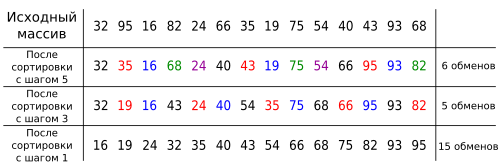
Ենթադրենք տրված է $A=(32,95,16,82,24,66,35,19,75,54,40,43,93,68)$ ցուցակ, և կատարվում է այս ցուցակի տեսակավորումը Շելլի մեթոդով, իսկ որպես $d$ նշանակաություն տրված են $5,3,1$։

Առաջին քայլում տեսակավորվում են $A$ - գրվածքները։ $A$-ի մեջ ընդգրկված բոլոր էլեմենտները, բաժանվում են 5 մասի։ Այսինքն $A_{5,1}=(32,66,40)$, $A_{5,2}=(95,35,43)$, $A_{5,3}=(16,19,93)$, $A_{5,4}=(82,75,68)$, $A_{5,5}=(24,54)$.

Երկրորդ քայլում նույնպես կատարվում է ստացված ցուցակի տեսակավորումը, սակայն մնացած գրվածքները արդեն բաժանվում են 3 մասի։

Ցանկի տեսակավրումը ավարտվում է սովորական ներդրման տեսակավորմամբ։

Ժամանակահատվածների ընտրությունը

Ալգորիթմի աշխատանքի միջին ժամանակը կախված է $d$ ժամանակահատվածների երկարություններից, որոնց վրա հետագայում պետք է գտնվեն $N$ կարողությամբ զանգվածի տեսակավորվող տարրերը։ Գոյություն ունեն այդ արժեքների ընտրության մի քանի մոտեցումներ.

• Ի սկզբանե Շելլի կողմից օգտագործվող ժամամանակահատվածների երկարության հաջորդականությունը այսպիսին էր՝ $~d_{1}=N/2,d_{i}=d_{i-1}/2,d_{0}=1$ վատագույն դեպքում, ալգորիթմի դժվարությունը կայանում է՝ $cN^{2}$-ում;
• Հիբբարդի կողմից առաջարկած հաջորդականությունը հետևյալն է՝ $~(2^{i}-1)/2\leq N/2,i\in \mathbb {N}$ բոլոր արժեքները։ Քայլերի մնան հաջորդականությունը բերում է $O(N^{3/2})$ բարդության ալգորիթմի;
• Սեդժիկի կողմից առաջարկած հաջորդականությունը հետևյալն է՝ $~d_{i}=9\cdot 2^{i}-9\cdot 2^{i/2}+1$, եթե i-ն հաշվելի է և $~d_{i}=8\cdot 2^{i}-6\cdot 2^{(i+1)/2}+1$, եթե i-ն անվերջ է։ Քայլերի նման հաջորդականության դեպքում ալգորիթմի միջին դժվարությունը կայանում է՝ $O(n^{7/6})$-ում, դասավորվածության վատագույն դեպքում՝ $O(n^{4/3})$: Սեդժիկի բանաձևի օգտագործման ժամանակ պետք է կանգ առնել inc[s-1] արժեքի վրա, եթե 3*inc[s] > size.;
• Պրատտի կողմից առաջարկած հաջորդականությունը հետևյալն է՝ $~2^{i}\cdot 3^{j}\leq N/2,i,j\in \mathbb {N}$ բոլոր արժեքները։ Այս դեպքում ալգորիթմի դյժարություն կայանում է $O(N(logN)^{2})$-ում;
• Մարցին Ցիուրի առաջարկած էմպիրիկ հաջորդականությունը՝(A102549-ի հաջորդականությունը OEIS-ում)։ $~d\in \left\{1,4,10,23,57,132,301,701,1750\right\}$; հանդիսանում է լավագույններից մեկը, մոտավորապես մինչև 4000 էլեմենտների տեսակավորման կարողությամբ։.;
• Ֆիբոնատտիի թվերի վրա հիմնված էմպիրիկ հաջորդականությունը `$~d\in \left\{F_{n}\right\}$;
• $~(3^{j}-1)/2\leq N/2$ բոլոր արժեքները, $j\in \mathbb {N}$։ Քայլերի նման հաջորդականությունը բերում է` $O(N^{3/2})$ բարդության ալգորիթմի։

Արտաքին հղումներ

• * Д. Кнут. Искусство программирования. Том 3. Сортировка и поиск, 2-е изд. Гл. 5.2.1. ISBN 5-8459-0082-4
• Анимированное представление алгоритма сортировки Шелла
• Представление алгоритма сортировки Шелла в виде танца (видео)