Լիսաժուի պատկերներ

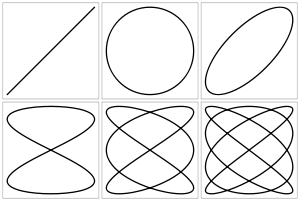
Լիսաժուի պատկերներ, երկու փոխուղղահայաց ուղղություններով միաժամանակ երկու ներդաշնակ տատանումների մասնակցող կետի փակ հետագծեր։ Առաջինն ուսումնասիրել է ֆրանսիացի ֆիզիկոս Ժյուլ Լիսաժուն (1822-1880)։ Լիսաժուի պատերների տեսքը կախված է երկու տատանումների պարբերությունների, փուլերի և ամպլիտուդների միջև եղած հարաբերակցությունից։ Պարզագույն դեպքում, երբ պարբերությունները հավասար են, Լիսաժուի պատկերներն էլիպսներ են, որոնք փուլերի տարբերության $0$ և $\pi$ արժեքների դեպքում վերածվում են ուղիղի հատվածի, իսկ ${\frac {\pi }{2}}$-ի դեպքում՝ շրջանագծի։ Եթե տատանումների պարբերությունները տարբեր են, բայց հարաբերում են ինչպես ամբողջ թվեր, ապա ստացվում են ավելի բարդ պատկերներ։ Այդ դեպքում Լիսաժուի պատկերների ն դրանց արտագծված ուղղանկյունների կողմերի հպման կետերի թիվը տալիս է երկու տատանումների պարբերությունների հարաբերությունը։ Լիսաժուի պատկերը կարելի է տեսնել օսցիլոգրաֆի էկրանի վրա։

Տես նաև

• Տատանումներ
• Ֆուկոյի ճոճանակ

Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից  (հ․ 4, էջ 623)։

Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Լիսաժուի պատկերներ» հոդվածին։