Կոսինուսների թեորեմ

Եռանկյուն

Կոսինուսների թեորեմը կապ է հաստատում եռանկյան կողմերի երկարությունների և երկու կողմերի միջև ընկած անկյան կոսինուսի միջև։

Թեորմի ձևակերպումը․

Եռանկյան ցանկացած կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին՝ հանած այդ կողմերի և նրանցով կազմված անկյան կոսինուսի կրկնապատիկ արտադրյալը՝

$c^2 = a^2 + b^2 - 2ab\cos\gamma\$։

Այն հանդիսանում է Պյութագորասի թեորեմի ընդհանրացված տարբերակը։ Երբ γ անկյունը ուղիղ է (90^° կամ π/2 ռադիան), կոսինուսների թեորեմը վերածվում է Պյութագորասի թեորեմին․

$c^2 = a^2 + b^2 \,$

Եռանկյան տարբեր կողմերի միջև ընկած անկյունները ընտրելիս՝ այն կստանա հետևյալ տեսքը․

$a^2 = b^2 + c^2 - 2bc\cos\alpha\,$

$b^2 = a^2 + c^2 - 2ac\cos\beta\,$։

Ապացույց եռանկյունաչափական մեթոդով

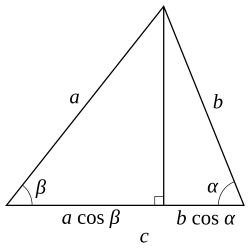
Նկար 1

c կողմին ուղղահայ տարեք (Նկար 1)․ այդ դեպքում

$c=a\cos\beta+b\cos\alpha\,.$

Երկու կողմերը բազմապատկելով c-ով՝, կստանաք

$c^2 = ac\cos\beta + bc\cos\alpha.\,$

Մյուս ուղղահայցները տանելով՝ կստանաք

$a^2 = ac\cos\beta + ab\cos\gamma,\,$

$b^2 = bc\cos\alpha + ab\cos\gamma.\,$

Վերջին երկու հավասարությունները գումարելով՝ կստանաք

$a^2 + b^2 = ac\cos\beta + bc\cos\alpha + 2ab\cos\gamma.\,$

Առաջին հավասարումը եկրկորդ հավասարումից հանելով՝ կստանանք

$a^2 + b^2 - c^2 = - ac\cos\beta - bc\cos\alpha+ ac\cos\beta + bc\cos\alpha + 2ab\cos\gamma\,$

որը կարելի է պարզեցնել հետևյալ տեսքի․

$c^2 = a^2 + b^2 - 2ab\cos\gamma.\,$

Այս ապացուցման հարմարությոնը կայանում է նրանում, որ կարիք չկա առանձին դիտարկել սուր և բութ γ անկյան դեպքերը։

Ապացույց վեկտորների օգտագործմամբ

Թեորեմը կարելի է ապացուցել՝ օգտվելով վեկտորների գումարման կանոնից և վեկտորների սկալյար արտադրյալի բանաձևից

$\vec b\cdot \vec c = \Vert \vec b\Vert\Vert\vec c\Vert\cos \theta$։

Նկար 2 — Վեկտորական եռանկյուն

Նկար 2-ից երևում է, որ

$\vec a=\vec b-\vec c\,,$։

Հաշվի առնելով դա՝

$\begin{align} \Vert\vec a\Vert^2 & = \Vert\vec b - \vec c\Vert^2 \\ & = (\vec b - \vec c)\cdot(\vec b - \vec c) \\ & = \Vert\vec b \Vert^2 + \Vert\vec c \Vert^2 - 2 \vec b\cdot\vec c. \end{align}$։

Այսպիսով, ստացանք

$\Vert\vec a\Vert^2 = \Vert\vec b \Vert^2 + \Vert\vec c \Vert^2 - 2 \Vert \vec b\Vert\Vert\vec c\Vert\cos(\theta), \,$

որը համարժեք է կոսինուսների թեորեմի հավասարմանը։