Պոտենցիալ հոր
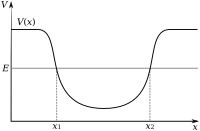
Պոտենցիալ հորը այն տիրույթն է, որը շրջափակում է պոտենցիալ էներգիայի լոկալ մինիմումը, կամ այլ կերպ ասած, տարածության սահմանափակ տիրույթ է, որտեղ մասնիկի պոտենցիալ էներգիայի արժեքներն ավելի փոքր են, քան այդ տիրույթից դուրս։ Պոտենցիալ հորում պարփակված էներգիան չի կարող փոխակերպվել այլ տիպի էներգիայի, քանի որ այն պարփակված է լոկալ մինիմումում, այսպիսով, պոտենցիալ հորի հիմնական հատկությունը մասնիկը պահելու ունակությունն է։ Այդպիսի կապված վիճակում մասնիկը միշտ շարժվում է հորի մեջ, այսինքն՝ մնում է տարածության վերջավոր տիրույթում (վերջավոր շարժում)։ Դասական ֆիզիկայում մասնիկը հորի սահմաններից դուրս գալ չի կարող։ Միաչափ շարժման դեպքում այն կատարում է պարբերական տատանումներ հավասարման արմատներով որոշվող դարձակետերի միջև։ Եռաչափ դեպքում մասնիկի շարժումն ունի բարդ բնույթ, իսկ կենտրոնասիմետրիկ դաշտում շարժումը տեղի է ունենում հարթության վրա։
Ընդհանուր մաթեմատիկական նկարագիրը[խմբագրել | խմբագրել կոդը]
Դիտարկենք ուղղանկյունաձև ֆունկցիայով նկարագրվող ուժային դաշտում մասնիկի շարժումը։
- ։
Այդպիսի ուժային դաշտը կոչվում է «ուղղանկյուն պատերով միաչափ պոտենցիալ հոր» կամ «պոտենցիալ արկղ», որտեղ - ն հորի խորությունն է։ Հորի ներսում Շրյոդինգերի հավասարման համար կունենանք
իսկ հորից դուրս
որտեղ ։ Այստեղ ։ Եթե , ապա էներգիայի սպեկտրը կլինի անընդհատ, շարժումն՝ անսահմանափակ, իսկ դեպքում սպեկտրը դիսկրետ է, շարժումը՝ սահմանափակ։
Մանրամասն հետազոտենք երկրորդ դեպքը։ Սկզբում դիտենք մասնիկի շարժումն անվերջ բարձր պոտենցիալ հորում՝ ։ Նկատի ունենալով, որ և -ի ածանցյալները պետք է լինեն վերջավոր, հավասարումից ստանում ենք
եզրային պայմանները։ Այսինքն գործ ունենք միայն (2) հավասարման հետ։ Լուծումը փնտրենք հետևյալ տեսքով
- ։
- և սահմանային պայմաններից ստանում ենք
- , որտեղից անմիջապես հետևում է՝
- ։
արժեքը պետք է բացառել, քանի որ նրա համար ալիքային ֆունկցիան դառնում է զրո։ -երը կարող են ունենալ նաև բացասական արժեքներ, սակայն դրանք նոր արդյունք չեն տալիս։ Իսկապես, -ը փոխարինելիս -ով էներգիան մնում է անփոփոխ, իսկ ալիքային ֆունկցիան փոխում է միայն նշանը։ -երի սահմանումներից էներգիայի համար ստանում ենք
- ։
Էներգիայի արժեքին համապատասխանող սեփական ֆունկցիան կլինի՝
- ։
Նորմավորման պայմանից ստացվում է
- ,
այսինքն
- ։
Սա ցույց է տալիս, որ քվանտմեխանիկական նկարագրությամբ պոտենցիալ հորում առաջանում են դիսկրետ վիճակներ, որոնցում կարող է գտնվել մասնիկը։
Քվանտային պոտենցիալ հոր[խմբագրել | խմբագրել կոդը]
Քվանտային նկարագրության դեպքում, մասնիկի ալիքային հատկությունների շնորհիվ, սահմանափակ շարժման տիրույթը կարող է գերազանցել պոտենցիալ հորի չափերը․ մասնիկը որոշ հավանականությամբ կարող է ներթափանցել այն տիրույթները, որտեղ (օրինակ, թունելային էֆեկտի շնորհիվ մասնիկը կարող է դուրս գալ վերջավոր հաստության «պատեր» ունեցող պոտենցիալ հորից)։ Առանձին դեպքերում (օրինակ, եռաչափ շարժում) սահմանափակ շարժումն անհնար է։ Այսպես, գնդային սիմետրիկ հորումում, քանի դեռ , շարժումն անսահմանափակ է (-ն հորի լայնությունն է, -ը՝ մասնիկի զանգվածը, -ը՝ Պլանկի հաստատունը)։ Հորի խորությունը կամ լայնությունը մեծացնելիս, երբ բերված անհավասարությունը նշանը փոխում է, առաջանում է սահմանափակ շարժման քվանտային վիճակ։ Միաչափ և երկչափ հորերի դեպքում կապված վիճակ գոյանում է և մեծությունների արժեքների ցանկացած փոխհարաբերության ժամանակ։
Տես նաև[խմբագրել | խմբագրել կոդը]
Գրականություն[խմբագրել | խմբագրել կոդը]
- Սահակյան Գ. Ս., Չուբարյան Է. Վ., Քվանտային մեխանիկա, ԵՊՀ հրատ., 2009, ISBN 978-5-8084-1133-3
- Buhro WE, Colvin VL (2003). «Semiconductor nanocrystals: Shape matters». Nat Mater. 2 (3): 138–9. Bibcode:2003NatMa...2..138B. doi:10.1038/nmat844. PMID 12612665.



































