Մասնակից:Gohar Piloyan/Ավազարկղ57

Հաշվումներում, սովորաբար հնարավոր է հաշվարկել երկու ֆունկցիաների գումարի, տարբերության, արտադրյալի, քանորդի կամ աստիճանի սահմանը՝ յուրաքանչյուր համապատասխան ֆունկցիայի առանձին սահմանների համապատասխան գումարը վերցնելով։ Օրինակ,

${\begin{aligned}\lim _{x\to c}{\bigl (}f(x)+g(x){\bigr )}&=\lim _{x\to c}f(x)+\lim _{x\to c}g(x),\\[3mu]\lim _{x\to c}{\bigl (}f(x)g(x){\bigr )}&=\lim _{x\to c}f(x)\cdot \lim _{x\to c}g(x),\end{aligned}}$

ինչպես նաև այլ թվաբանական գործողությունների համար. սա երբեմն կոչվում է հանրահաշվական սահմանային թեորեմ: Այնուամենայնիվ, որոշակի սահմանափակ արժեքների որոշակի գումարներ չեն կարող այս կերպ հաշվարկվել, և յուրաքանչյուր ֆունկցիայի սահմանն առանձին իմանալը բավարար չէ գումարի սահմանը որոշելու համար: Այս կոնկրետ իրավիճակներում սահմանը համարվում է անորոշ ձևով, որը նկարագրված է ոչ պաշտոնական արտահայտություններում։

${\frac {0}{0}},~{\frac {\infty }{\infty }},~0\times \infty ,~\infty -\infty ,~0^{0},~1^{\infty },{\text{ or }}\infty ^{0},$

որտեղ յուրաքանչյուր արտահայտություն նշանակում է ֆունկցիայի սահման, որը կառուցված է երկու ֆունկցիաների թվաբանական գումարի միջոցով, որոնց սահմանները համապատասխանաբար նշված են։

Այս անորոշ ձևերից որևէ մեկն ընդունող սահմանը կարող է ձգտել զրոյի, կարող է ձգտել դեպի ցանկացած վերջավոր արժեք, կարող է ձգտել դեպի անսահմանություն կամ կարող է ձգտել՝ կախված ներգրավված հատուկ ֆունկցիաներից: Սահմանի օրինակ, որը միանշանակորեն ձգտում է դեպի անսահմանություն ${\textstyle \lim _{x\to 0}1/x^{2}=\infty ,}$ չի համարվում անորոշ։ Տերմինն ի սկզբանե ներմուծվել է Կոշիի աշակերտ Մոյնոյի կողմից 19-րդ դարի կեսերին։

Անորոշ ձևի ամենատարածված օրինակը երկու ֆունկցիաների քանորդն է, որոնցից յուրաքանչյուրը համընկնում է զրոյի: Այս անորոշ ձևը նշվում է $0/0$.Օրինակ, ինչպես 𝑥 ձգտում է 0, գործակիցները $x/x^{3}$, $x/x$, and $x^{2}/x$ ձգտում է $\infty$, $1$, և $0$ համապատասխանաբար։ Յուրաքանչյուր դեպքում, եթե համարիչի և հայտարարի սահմանները փոխարինվեն. $0/0$, ստացված արտահայտությունը անորոշ է։ Այս առումով, $0/0$ կարող է ընդունել արժեքներ $0$, $1$, or $\infty$, համարիչի և հայտարարի մեջ դնելու գործառույթների համապատասխան ընտրություն: Գործառույթների մի զույգ, որի սահմանը ցանկացած որոշակի արժեք է, կարող է իրականում գտնվել: Նույնիսկ ավելի զարմանալի է, հավանաբար, որ երկու ֆունկցիաների գործակիցները կարող են իրականում ձգտել դեպի անսահմանություն: Օրինակ, $x\sin(1/x)/x$.

Այսպիսով, այն փաստը, որ երկու ֆունկցիաներ $f(x)$ և $g(x)$ ձգտեն $0$ ինչպես $x$ մոտենում է որոշ սահմանային 𝑐 կետի,  սահմանը որոշելու համար բավարար չէ։

Արտահայտությունը, որն առաջանում է հանրահաշվական սահմանային թեորեմը կիրառելուց բացի այլ եղանակներով, կարող է ունենալ անորոշ ձևի նույն ձևը: Այնուամենայնիվ, տեղին չէ արտահայտությունն անվանել «անորոշ ձև», եթե արտահայտությունն արված է սահմանների որոշման համատեքստից դուրս: Օրինակ է արտահայտություն $0^{0}$. Անկախ նրանից, թե այս արտահայտությունը մնացել է չսահմանված, թե սահմանվել է հավասար 1, կախված է կիրառման ոլորտից և կարող է տարբեր լինել: Նշենք, որ 0∞․  իսկ անսահմանություն պարունակող այլ արտահայտությունները անորոշ ձևեր չեն:

Որոշ օրինակներ

Անորոշ ձև 0/0

• 
  Նկար 1
• 
  Նկար 2
• 
  Նկար 2
• 
  Նկար 4
• 
  Նկար 5
• 
  Նկար 6

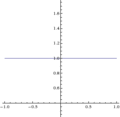
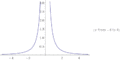
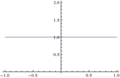
Անորոշ ձև $0/0$ շատ տարածված է, քանի որ այն հաճախ առաջանում է ածանցյալ գործիքների գնահատման ժամանակ՝ օգտագործելով դրանց սահմանը:

Ինչպես նշվեց վերևում, մինչդեռ սա բավական է ցույց տալու համար $0/0$ iանորոշ ձև է։ Այս անորոշ ձևով այլ օրինակներ ներառում են թվի ուղղակի փոխարինում $x$-ով։ Այս արտահայտություններից որևէ մեկի մոտեցումները ցույց են տալիս, որ սրանք օրինակներ են, որոնք համապատասխանում են անորոշ ձևին $0/0$, բայց այս սահմանները կարող են ենթադրել շատ տարբեր արժեքներ, ցանկալի արժեք 𝑎 ։ Այս անորոշ ձևի $\infty$ համար, կարելի է նաև արժեք ստանալ (անսահմանության շեղման իմաստով)։

Անորոշ ձև 0⁰

• 
  Նկար 7
• 
  Նկար 8

Հետևյալ սահմանները ցույց են տալիս, որ $0^{0}$արտահայտությունը անորոշ ձև է։

Այսպիսով, ընդհանուր առմամբ, իմանալով, որ $\textstyle \lim _{x\to c}f(x)\;=\;0$ and $\textstyle \lim _{x\to c}g(x)\;=\;0$ սահմանը գնահատելու համար բավարար չէ։

Եթե ֆունկցիաներ $f$ և $g$ վերլուծական են $c$-ին և $f$ -ի համար դրական է 𝑥  բավականաչափ մոտ (բայց ոչ հավասար) 𝑐, ապա սահման $f(x)^{g(x)}$ կլիմի $1$։ Հակառակ դեպքում սահմանը գնահատելու համար օգտագործեք ստորև բերված աղյուսակի փոխակերպումը:

Արտահայտություններ, որոնք անորոշ ձևեր չեն

Արտահայտությունը $1/0$ սովորաբար չի դիտվում որպես անորոշ ձև, եթե սահման $f/g$ գոյություն ունի, ապա դրա արժեքի վերաբերյալ երկիմաստություն չկա, քանի որ այն միշտ տարբերվում է: Մասնավորապես, եթե $f$ ձգտում է $1$ և $g$ ձգտում է $0,$ ապա $f$ և $g$ կարող է ընտրվել այնպես, որ.

1. $f/g$ ձգտում է $+\infty$,
2. $f/g$ ձգտում է $-\infty$;
3. Սահմանը գոյություն չունի:

Յուրաքանչյուր դեպքում բացարձակ արժեքը $|f/g|$ ձգտում է $+\infty$, և այսպես գործակիցը $f/g$ պետք է շեղվի՝ ընդլայնված իրական թվերի իմաստով (պրոյեկտիվ ընդլայնված իրական գծի շրջանակներում սահմանը անստորագիր անվերջությունն է $\infty$ բոլոր երեք դեպքերում)։ Նման ձևի ցանկացած արտահայտություն $a/0$ -ն $a\neq 0$ հետ (այդ թվում $a=+\infty$ և $a=-\infty$) անորոշ ձև չէ, քանի որ նման արտահայտություն առաջացնող գործակիցը միշտ տարբերվելու է:

$0^{\infty }$ արտահայտությունը անորոշ ձև չէ. Արտահայտություն՝ $0^{+\infty }$ հաշվի առնելով ստացված $\lim _{x\to c}f(x)^{g(x)}$ տալիս է $0,$ սահման պայմանով, որ $f(x)$ մնում է ոչ բացասական, քանի որ $x$ ձգտում է $c$։ Արտահայտություն՝ $0^{-\infty }$ նմանապես համարժեք է $1/0$; եթե $f(x)>0$ ինչպես 𝑥  ձգտում է 𝑐, սահմանը ստացվում է $x$ ձգտում է $c$, սահմանը ստացվում է $+\infty$։

Տեսնելու համար, թե $L=\lim _{x\to c}f(x)^{g(x)},$ որտեղ $\lim _{x\to c}{f(x)}=0,$ և $\lim _{x\to c}{g(x)}=\infty .$ Վերցնելով երկու կողմերի բնական լոգարիթմը և օգտագործելով $\lim _{x\to c}\ln {f(x)}=-\infty ,$ մենք դա ստանում ենք $\ln L=\lim _{x\to c}({g(x)}\times \ln {f(x)})=\infty \times {-\infty }=-\infty ,$ նշանակում է, որ $L={e}^{-\infty }=0.$

Անորոշ ձևերի գնահատում

Անորոշ ածանցյալը չի նշանակում, որ սահմանը գոյություն չունի, ինչպես ցույց են տալիս վերը նշված օրինակներից շատերը: Շատ դեպքերում, հանրահաշվական մոտարկումը, Լոպիտալիի կանոնը կամ այլ մեթոդներ կարող են օգտագործվել արտահայտությունը շահարկելու համար, որպեսզի սահմանը հնարավոր լինի գնահատել:

Անսահման փոքրին համարժեք

Երբ երկու փոփոխական $\alpha$ և $\beta$ նույն սահմանային կետում ձգտում են զրոյի և $\textstyle \lim {\frac {\beta }{\alpha }}=1$,դրանք կոչվում են համարժեք անվերջ փոքր (համարժեք. $\alpha \sim \beta$).

Ընդ որում, եթե փոփոխականներ $\alpha '$ և $\beta '$ այնպիսին են, որ $\alpha \sim \alpha '$ և $\beta \sim \beta '$։

Ահա մի հակիրճ ապացույց.

Ենթադրենք կան երկու համարժեք անվերջ փոքրեր $\alpha \sim \alpha '$ և $\beta \sim \beta '$.

$\lim {\frac {\beta }{\alpha }}=\lim {\frac {\beta \beta '\alpha '}{\beta '\alpha '\alpha }}=\lim {\frac {\beta }{\beta '}}\lim {\frac {\alpha '}{\alpha }}\lim {\frac {\beta '}{\alpha '}}=\lim {\frac {\beta '}{\alpha '}}$

Անորոշ ձևի գնահատման համար $0/0$, կարելի է օգտագործել հետևյալ փաստերը համարժեք անվերջ փոքրերի վերաբերյալ (օրինակ., $x\sim \sin x$ եթե x մոտենում է զրոյին):

Օրինակ,

${\begin{aligned}\lim _{x\to 0}{\frac {1}{x^{3}}}\left[\left({\frac {2+\cos x}{3}}\right)^{x}-1\right]&=\lim _{x\to 0}{\frac {e^{x\ln {\frac {2+\cos x}{3}}}-1}{x^{3}}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln {\frac {2+\cos x}{3}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln \left({\frac {\cos x-1}{3}}+1\right)\\&=\lim _{x\to 0}{\frac {\cos x-1}{3x^{2}}}\\&=\lim _{x\to 0}-{\frac {x^{2}}{6x^{2}}}\\&=-{\frac {1}{6}}\end{aligned}}$

2-րդ հավասարության մեջ, $e^{y}-1\sim y$ ,որտեղ $y=x\ln {2+\cos x \over 3}$ երբ y-ը մոտենում է 0-ին և $y\sim \ln {(1+y)}$ ,որտեղ $y={{\cos x-1} \over 3}$ օգտագործվում է 4-րդ հավասարության մեջ, և $1-\cos x\sim {x^{2} \over 2}$ օգտագործվում է 5-րդ հավասարության մեջ։

Լոպիտալի կանոն

Լոպիտալի կանոնը անորոշ ձևերի $0/0$ և $\infty /\infty$ գնահատման ընդհանուր մեթոդ է։ Այս կանոնը սահմանում է, որ (համապատասխան պայմաններում) $f'$ և $g'$, $f$ և $g$-ի ածանցյալները (Նկատի ունեցեք, որ այս կանոնը չի տարածվում $\infty /0$, $1/0$ և այլ արտահայտությունների վրա, քանի որ այս արտահայտությունները անորոշ ձևեր չեն)։ Այս ածանցյալները թույլ կտան կատարել հանրահաշվական պարզեցում և ի վերջո գնահատել սահմանը:

Լոպիտալի կանոնը կարող է կիրառվել նաև այլ անորոշ ձևերի վրա՝ նախ օգտագործելով համապատասխան հանրահաշվական փոխակերպումը։ Օրինակ՝ ձևը գնահատելու համար և այլն, քանի որ այս արտահայտությունները անորոշ ձևեր չեն:) Այս ածանցյալները թույլ կտան կատարել հանրահաշվական պարզեցում և ի վերջո գնահատել սահմանը:

Լոպիտալի կանոնը կարող է կիրառվել նաև այլ անորոշ ձևերի վրա՝ նախ օգտագործելով համապատասխան հանրահաշվական փոխակերպումը։ Օրինակ՝ 0⁰ ձևը գնահատելու համար։ Աջ կողմը ձև է $\infty /\infty$, Լոպիտալի կանոնը կիրառվում է դրա համար. Նկատի ունեցեք, որ այս հավասարումը վավեր է (քանի դեռ սահմանված է աջ կողմը), քանի որ բնական լոգարիթմ (ln) շարունակական ֆունկցիա է. կապ չունի, թե որքան լավ է իրեն պահում 𝑓  և 𝑔  կարող է (կամ չի կարող) լինել այնքան ժամանակ, որքանմ 𝑓  ասիմպտոտիկ դրական է: (լոգարիթմների տիրույթը բոլոր դրական իրական թվերի բազմությունն է):

Չնայած Լոպիտալի կանոնը վերաբերում է երկուսին էլ $0/0$ և $\infty /\infty$, Այս ձևերից մեկը կարող է ավելի օգտակար լինել, քան մյուսը կոնկրետ դեպքում (հետագայում հանրահաշվական պարզեցման հնարավորության պատճառով): Կարող է փոխվել այս ձևերի միջև՝ փոխակերպվելով $f/g$ to $(1/g)/(1/f)$։

Անորոշ ձևերի ցանկ

Հետևյալ աղյուսակը թվարկում է ամենատարածված անորոշ ձևերը և Լոպիտալի կանոնը կիրառելու եղանակները,

Անորոշ ձև	Պայմաններ	Փոխակերպում դեպի $0/0$	Փոխակերպում դեպի $\infty /\infty$
$0$$0$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!$	—	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$
$\infty$$\infty$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$	—
$0\cdot \infty$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {g(x)}{1/f(x)}}\!$
$\infty -\infty$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!$	$\lim _{x\to c}(f(x)-g(x))=\ln \lim _{x\to c}{\frac {e^{f(x)}}{e^{g(x)}}}\!$
$0^{0}$	$\lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$
$1^{\infty }$	$\lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$
$\infty ^{0}$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$