Էլիպս

ў

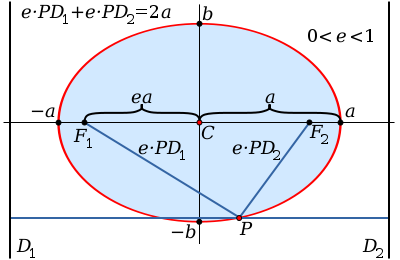
Էլիպս երկրաչափական պատկեր է: Էլիպս է կոչվում հարթության այն կետերի երկրաչափական տեղը, որոնց հեռավորությունների գումարը տրված երկու
$F_1$ և $F_2$ կետերից հաստատուն է և մեծ է $F_1 F_2$ հատվածի երկարությունից: Այդ հաստատունը կնշանակենք 2a-ով: $F_1$-ը և $F_2$-ը կոչվում են էլիպսի ֆոկուսներ, իսկ $F_1 F_2$ հատվածի երկարությունը կնշանակենք 2c-ով, և կանվանենք ֆոկուսային հեռավորություն:

Էլիպսի հավասարումը

Հարթության վրա ուղղանկյուն կոորդինատային համակարգն ընտրենք այնպես , որ Ox առանցքն անցնի $F_1$ և $F_2$ կետերով , իսկ Oy առանցքը` $F_1 F_2$ հատվածի միջնակետով : Այս դեպքում , ըստ սահմանման , էլիպսի ցանկացած P(x, y) կետի համար`

P$F_1$ + P$F_2$ = 2a

Հաշվի առնելով , որ $F_1$ կետի կոորդինատներն են $F_1$(-c;0) , իսկ $F_2$ կետինը $F_1$(c;0), երկու կետի հեռավորության բանաձևից ստանում ենք`

$\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} = 2a$

Սա էլ հենց հանդիսանում է էլիպսի հավասարումը ընտրված կոորդինատային համակարգում: Փորձենք այն գրել կոմպակտ տեսքով: Դրա համար երկրորդ գումարելին տեղափոխենք հավասարման աջ մաս և երկու կողմերը բարձրացնենք քառակուսի`

$~(x+c)^2+y^2 = 4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2$

Պարզեցումներից հետո ստանում ենք`

$~(a^2-c^2)x^2+a^2y^2 = a^2(a^2-c^2)$

Քանի որ $~a > c$, ապա $~a^2-c^2$ > 0 : Նշանակենք $~b^2 = a^2-c^2$, ուստի $b = \sqrt{a^2-c^2}$ հետևաբար հավասարումը կընդունի հետևյալ տեսքը`

$~b^2x^2+a^2y^2 = a^2b^2$

կամ

$~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

որը կոչվում է էլիպսի կանոնական հավասարում : Այստեղ 2a-ն և 2b-ն կոչում են էլիպսի համապատասխանաբար մեծ և փոքր առանցքների երկարություններ, իսկ կոորդինատների սկզբնակետը` քլիպսի կենտրոն : $e = \frac{c}{a}$ թիվը կոչվում է էլիպսի էքսցենտրիսիտետ : Կոորդինատային առանցքների հետ հատման կետերը կոչվում են էլիպսի գագաթներ :

Դիտողություն

Նշենք, որ իրականում մենք ցույց տվեցինք, որ(1) հավասարմանը բավարարող ցանկացած M(x;y) բավարարում է նաև (2) հավասարմանը: Կարելի է ցույց տալ, որ ճիշտ է նաև հակառակը, այսինքն (2)-ին բավարարող ցանկացած M(x;y) կետ բավարարում է նաև (1)-ին: Օրինակ: Գտնել հետևյալ հավասարումով տրված էլիպսի ֆոկուսների հեռավորությունը և էքսցենտրիսիտետը:

$~3x^2+4y^2 = 5$

Լուծում

հավասարման երկու մասը բաժանելով 5-ի` ստանում ենք

$\frac{x^2}{\frac{5}{3}} +\frac{y^2}{\frac{5}{4}}=1$

ուստի $a = \sqrt{\frac{5}{3}}$; $b = \sqrt{\frac{5}{4}}$

$~{c^2}={a^2} - {b^2} = {\frac{5}{3}} - {\frac{5}{4}} = {\frac{5}{12}}$ ,$~2c=2\sqrt{\frac{5}{12}}$

$e = \sqrt{\frac{5}{12}} : \sqrt{\frac{5}{3}}$ = ${\frac{1}{2}}$