Հյույգենս-Ֆրենելի սկզբունք

Հյույգենս-Ֆրենելի սկզբունք, Հյույգենսի սկզբունք, ալիքային տեսության հիմնական պոստուլատը, ալիքների տարածման խնդիրների լուծման մոտավոր մեթոդ, հիմնականում վերաբերում է լուսային ալիքներին. նկարագրում և բացատրում է ալիքների, մասնավորապես՝ լույսի տարածման մեխանիզմը։
Նկարագրությունը[խմբագրել | խմբագրել կոդը]
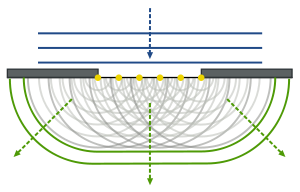
Հյույգենս Ֆրենելի սկզբունքը 1678 թ. Քրիստիան Հյույգենսի կողմից ձևակերպված սկզբունքի զարգացումն է. մակերևույթի յուրաքանչյուր կետ, որին հասել է լուսային ալիքը, ալիքների երկրորդային աղբյուր է։ Երկրորդային ալիքների պարուրիչը ժամանակի հաջորդ պահին դառնում է ալիքի ճակատ։ Հյույգենսի սկզբունքը հնարավորություն է տալիս խնդիրներ լուծելիս ամբողջ ալիքային պրոցեսի փոխարեն դիտարկել կամայականորեն ընտրված ալիքային մակերևույթ։
Հյույգենսի սկզբունքով ալիքների տարածման բացատրությունը համապատասխանում է երկրաչափական օպտիկայի օրենքների հետ, սակայն դիֆրակցիայի երևույթը հնարավոր չէ բացատրել դրանով։
1815 թ. Օգյուստեն Ֆրենելը լրացրեց այն՝ ներմուծելով տարրական ալիքների կոհերենտության և ինտերֆերենցիայի հասկացությունները, ինչը թույլ տվեց Հյույգենս-Ֆրենելի սկզբունքի հիման վրա դիտարկել նաև դիֆրակցիոն երևույթները։
Հյույգենս-Ֆրենելի սկզբունքը ձևակերպվում է հետևյալ կերպ.
Ալիքային ճակատի յուրաքանչյուր տարր կարելի է դիտարկել որպես երկրորդային գնդային ալիքներ ծնող երկրորդային գրգռման կենտրոն, իսկ արդյունարար լուսային դաշտը տարածության յուրաքանչյուր կետում կորոշվի այդ ալիքների ինտերֆերենցիայով։
Գուստավ Կիրխհոֆը Հյույգենսի սկզբունքին տվեց խիստ մաթեմատիկական տեսք՝ ցույց տալով, որ այն կարելի է համարել Կիրխհոֆի ինտեգրալային թեորեմ կոչված թեորեմի մոտավոր ձևը։
Համասեռ իզոտրոպ տարածությունում կետային աղբյուրի ալիքի ճակատը գնդոլորտ է։ Կետային աղբյուրից տարածվող գնդային ալիքի գրգռման ամպլիտուդը բոլոր կետերում միևնույնն է։
Հյույգենսի սկզբունքի հետագա ընդհանրացումը և զարգացումը ըստ հետագծերով ինտեգրալների ձևակերպումն է, ինչը հիմք է հանդիսանում ժամանակակից քվանտային մեխանիկայի համար։
Տես նաև[խմբագրել | խմբագրել կոդը]
Գրականություն[խմբագրել | խմբագրել կոդը]
- Լանդսբերգ Գ. Ս., Օպտիկա, Ե., 1973 (Ֆիզիկայի ընդհանուր դասընթաց, հ. 3)։
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 6, էջ 439)։ |
