«Սեղան (երկրաչափություն)»–ի խմբագրումների տարբերություն
չ +{{անաղբյուր}} |
No edit summary |
||
| Տող 9. | Տող 9. | ||
Սեղանները կարող են լինել հավասարասրուն և ուղղանկյուն։ Հավասարասրուն սեղան է կոչվում այն սեղանը, որի սրունքները (կողմնային կողերը) հավասար են միմյանց։ Իսկ ուղղանկյուն սեղան է կոչվում այն սեղանը, որի սրունքներից մեկը ուղղահայաց է հիմքերին։ |
Սեղանները կարող են լինել հավասարասրուն և ուղղանկյուն։ Հավասարասրուն սեղան է կոչվում այն սեղանը, որի սրունքները (կողմնային կողերը) հավասար են միմյանց։ Իսկ ուղղանկյուն սեղան է կոչվում այն սեղանը, որի սրունքներից մեկը ուղղահայաց է հիմքերին։ |
||
== Варианты определения == |
|||
Существует и другое определение трапеции. |
|||
Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны<ref>[http://www.bymath.net/studyguide/geo/sec/geo8.htm Вся элементарная математика]</ref><ref>[http://mathworld.wolfram.com/Trapezoid.html Wolfram MathWorld]</ref>. Согласно этому определению, [[параллелограмм]] и [[прямоугольник]] — частные случаи трапеции. Приведённые ниже формулы верны для обоих определений трапеции. |
|||
== Связанные определения == |
|||
=== Элементы трапеции === |
|||
[[Պատկեր:Трапеция и диагонали.png|thumb|300px|right|Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой]] |
|||
* Параллельные противоположные стороны называются '''основаниями''' трапеции. |
|||
* Две другие стороны называются '''боковыми сторонами'''. |
|||
* Отрезок, соединяющий середины боковых сторон, называется '''[[Средняя линия трапеции|средней линией]]''' трапеции. |
|||
=== Виды трапеций === |
|||
* Трапеция, у которой боковые стороны равны, называется '''равнобедренной''' трапецией (реже '''равнобокой'''<ref>{{Книга|автор=Коллектив авторов|заглавие=Современный справочник школьника. 5-11 классы. Все предметы|ссылка=https://books.google.com/books?id=YRmFAQAAQBAJ|издательство=Litres|год=2015-09-03|страницы=82|страниц=482|столбцы=|isbn=9785457410022}}</ref> или '''равнобочной'''<ref>{{Книга|автор=М. И. Сканави|заглавие=Элементарная математика|ссылка=https://books.google.com/books?id=6EX6AgAAQBAJ&pg=PA437|издательство=|год=2013|страницы=437|страниц=611|isbn=9785458254489}}</ref> трапецией). |
|||
* Трапеция, имеющая [[Прямой угол|прямые]] углы при боковой стороне, называется '''прямоугольной'''. |
|||
<gallery> |
|||
Trapezoid2 1.png|Равнобедренная трапеция |
|||
Trapezoid1.png|Прямоугольная трапеция |
|||
</gallery> |
|||
== Общие свойства == |
|||
{{Mainref|<ref>{{книга | заглавие = Четырёхугольники | ссылка =http://math4school.ru/chetyrehugolniki.html |
|||
}}</ref>}} |
|||
* Средняя линия трапеции параллельна основаниям и равна их полусумме. |
|||
* Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. |
|||
* (Обобщённая [[теорема Фалеса]]). Параллельные прямые, пересекающие стороны [[угол|угла]], отсекают от сторон угла пропорциональные отрезки. |
|||
* В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. |
|||
* Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен <math>\frac{2xy}{x+y}</math> [[Среднее гармоническое|среднему гармоническому]] длин оснований трапеции (формула Буракова). |
|||
* Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой. |
|||
* Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их [[wikt:полуразность|полуразности]]. |
|||
* Треугольники, лежащие на основаниях при пересечении диагоналей, [[Подобие треугольников|подобные]]. |
|||
* Треугольники, лежащие на боковых сторонах, равновеликие. |
|||
* Если отношение оснований равно <math>K</math>, то отношение площадей треугольников, лежащих на основаниях, равно <math>K^2</math>. |
|||
* Высота трапеции определяется формулой: |
|||
:: <math> h=\sqrt{c^2-\frac 14 \left ( \frac{c^2-d^2}{b-a}+b-a\right )^2}</math> |
|||
: где <math> b </math> — большее основание, <math> a </math> — меньшее основание, <math> c </math> и <math> d </math> — боковые стороны. |
|||
* Диагонали трапеции <math> d_1</math> и <math> d_2 </math> связаны со сторонами соотношением: |
|||
:: <math>d_1^2+d_2^2=2ab+c^2+d^2 </math> |
|||
: Их можно выразить в явном виде: |
|||
:: <math> d_1=AC=\sqrt{ab+d^2+\frac{b(c^2-d^2)}{b-a}}</math> |
|||
:: <math> d_2=BD=\sqrt{ab+c^2-\frac{b(c^2-d^2)}{b-a}}</math> |
|||
: Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами: |
|||
:: <math>a=\sqrt{\frac{(c^2-d_1^2)^2-(d^2-d_2^2)^2}{2(c^2-d^2+d_1^2-d_2^2)}}</math> |
|||
:: <math>b=\sqrt{\frac{(c^2-d_2^2)^2-(d^2-d_1^2)^2}{2(c^2-d^2-d_1^2+d_2^2)}}</math> |
|||
:: а при известных основаниях и диагоналях боковые стороны следующие: |
|||
:: <math>c=\sqrt{\frac{a(d_2^2-b^2)+b(d_1^2-a^2)}{a+b}}</math> |
|||
:: <math>d=\sqrt{\frac{a(d_1^2-b^2)+b(d_2^2-a^2)}{a+b}}</math> |
|||
: Если же известна высота <math> h </math>, то |
|||
:: <math>d_1=\sqrt{b^2+d^2-2b\sqrt{d^2-h^2}}=\sqrt{h^2+\left (b-\sqrt{d^2-h^2} \right )^2}</math> |
|||
:: <math>d_2=\sqrt{b^2+c^2-2b\sqrt{c^2-h^2}}=\sqrt{h^2+\left (b-\sqrt{c^2-h^2} \right )^2}</math> |
|||
== Свойства и признаки равнобедренной трапеции == |
|||
Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий: |
|||
* прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции); |
|||
* высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований; |
|||
* углы при любом основании равны; |
|||
* сумма противоположных углов равна 180°; |
|||
* длины диагоналей равны; |
|||
* вокруг этой трапеции можно описать окружность; |
|||
* вершинами этой трапеции также являются вершины некоторого [[антипараллелограмм]]а. |
|||
Кроме того |
|||
* если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований. |
|||
== Вписанная и описанная окружность == |
|||
{{Нет ссылок|В этом разделе|дата=6 июля 2015}} |
|||
* Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно [[Вписанная окружность|вписать]] [[окружность]]. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований). |
|||
* В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°. |
|||
* Если трапеция равнобедренная, то около неё можно [[Описанная окружность|описать]] [[окружность]]. |
|||
* Радиус описанной окружности равнобедренной трапеции:{{нет АИ|6|07|2015}} |
|||
:: <math>R=\frac{bcd_1}{4\sqrt{p(p-b)(p-c)(p-d_1)}}=\sqrt{\frac{ab+c^2}{4-\left ( \frac{b-a}{c}\right )^2}}</math> |
|||
: где <math>p=\frac 12 (b+c+d_1) \, , \, c</math> — боковая сторона, <math>b</math> — бо́льшее основание, <math>a</math> — меньшее основание, <math> d_1=d_2 </math> — диагонали равнобедренной трапеции. |
|||
* Если <math>a+b=2c </math>, то в равнобедренную трапецию можно вписать окружность радиуса |
|||
:: <math>r=\frac h2=\frac{\sqrt{ab}}{2}</math> |
|||
* Если в трапецию [[Вписанная окружность|вписана]] [[окружность]] с радиусом <math>r</math>, и она делит боковую сторону точкой касания на два отрезка — <math>v</math> и <math>w</math> — то <math>r = \sqrt{vw}</math>. |
|||
== Սեղանի մակերեսը == |
== Սեղանի մակերեսը == |
||
06:25, 12 Օգոստոսի 2018-ի տարբերակ
| Այս հոդվածն աղբյուրների կարիք ունի։ Դուք կարող եք բարելավել հոդվածը՝ գտնելով բերված տեղեկությունների հաստատումը վստահելի աղբյուրներում և ավելացնելով դրանց հղումները հոդվածին։ Անհիմն հղումները ենթակա են հեռացման։ |
 Անվան այլ կիրառումների համար տե՛ս՝ Սեղան (այլ կիրառումներ)
Անվան այլ կիրառումների համար տե՛ս՝ Սեղան (այլ կիրառումներ)

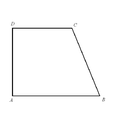
Սեղան, երկրաչափական պատկեր, ուռուցիկ քառանկյուն, որի երկու հակադիր կողմերը զուգահեռ են միմյանց, իսկ մյուս երկուսը՝ ոչ։
Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր։ (Օրինակ՝ նկարում AB-ն սեղանի փոքր հիմքն է, DC-ն՝ մեծ հիմքը)
Սեղանի ոչ զուգահեռ կողմերը կոչվում են սրունքներ։ (Օրինակ՝ նկարում AD-ն, BC-ն)
Սեղանները կարող են լինել հավասարասրուն և ուղղանկյուն։ Հավասարասրուն սեղան է կոչվում այն սեղանը, որի սրունքները (կողմնային կողերը) հավասար են միմյանց։ Իսկ ուղղանկյուն սեղան է կոչվում այն սեղանը, որի սրունքներից մեկը ուղղահայաց է հիմքերին։
Варианты определения
Существует и другое определение трапеции.
Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны[1][2]. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Приведённые ниже формулы верны для обоих определений трапеции.
Связанные определения
Элементы трапеции

- Параллельные противоположные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Виды трапеций
- Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой[3] или равнобочной[4] трапецией).
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
-
Равнобедренная трапеция
-
Прямоугольная трапеция
Общие свойства
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии.
- (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен среднему гармоническому длин оснований трапеции (формула Буракова).
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
- Треугольники, лежащие на основаниях при пересечении диагоналей, подобные.
- Треугольники, лежащие на боковых сторонах, равновеликие.
- Если отношение оснований равно , то отношение площадей треугольников, лежащих на основаниях, равно .
- Высота трапеции определяется формулой:
- где — большее основание, — меньшее основание, и — боковые стороны.
- Диагонали трапеции и связаны со сторонами соотношением:
- Их можно выразить в явном виде:
- Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:
- а при известных основаниях и диагоналях боковые стороны следующие:
- Если же известна высота , то
Свойства и признаки равнобедренной трапеции
Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:
- прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции);
- высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
- углы при любом основании равны;
- сумма противоположных углов равна 180°;
- длины диагоналей равны;
- вокруг этой трапеции можно описать окружность;
- вершинами этой трапеции также являются вершины некоторого антипараллелограмма.
Кроме того
- если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная и описанная окружность
- Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
- В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
- Если трапеция равнобедренная, то около неё можно описать окружность.
- Радиус описанной окружности равнобедренной трапеции:Կաղապար:Нет АИ
- где — боковая сторона, — бо́льшее основание, — меньшее основание, — диагонали равнобедренной трапеции.
- Если , то в равнобедренную трапецию можно вписать окружность радиуса
- Если в трапецию вписана окружность с радиусом , и она делит боковую сторону точкой касания на два отрезка — и — то .
Սեղանի մակերեսը
- և սեղանի հիմքերի և — բարձրության միջոցով՝
- միջին գծի և բարձրության միջոցով՝
- միջին գիծը հավասար է հիմքերի կիսագումարին՝
- սեղանի մակերեսը , հիմքերի և և ոչ զուգահեռ կողմերի միջոցով՝
- հավասարակողմ սեղանի մակերեսը ներգծված շրջանագծի շառավիղի և հիմքին կից անկյան միջոցով՝
- մասնավորապես, եթե տվյալ անկյունը 30° է, ապա
- հավասարակողմ սեղանի մակերեսը կողմի և մեծ հիմքին կից անկյան միջացով։
- ↑ Вся элементарная математика
- ↑ Wolfram MathWorld
- ↑ Коллектив авторов Современный справочник школьника. 5-11 классы. Все предметы. — Litres, 2015-09-03. — С. 82. — 482 с. — ISBN 9785457410022
- ↑ М. И. Сканави Элементарная математика. — 2013. — С. 437. — 611 с. — ISBN 9785458254489