«Գրաֆների տեսություն»–ի խմբագրումների տարբերություն
չ →Կիրառություններ: կաղապարներ |
լուսանկար |
||
| Տող 1. | Տող 1. | ||
[[File:Complete graph K6.svg|thumb|Վեց գագաթանի [[լրիվ գրաֆ]] <math>K_6</math>]] |
|||
[[Մաթեմատիկա]]յում և [[Ինֆորմատիկա|համակարգչային գիտության]] մեջ '''գրաֆների տեսությունը''' ուսումնասիրում է [[գրաֆներ]]ը, որոնք օբյեկտների միջև զույգ առ զույգ կապերը մոդելավորող մաթեմատիկական օբյեկտներ են: Գրաֆը կազմված է «գագաթներից» (կամ «հանգույցներից») և «կողերից», որոնք միացնում են գագաթների որոշ զույգեր: |
[[Մաթեմատիկա]]յում և [[Ինֆորմատիկա|համակարգչային գիտության]] մեջ '''գրաֆների տեսությունը''' ուսումնասիրում է [[գրաֆներ]]ը, որոնք օբյեկտների միջև զույգ առ զույգ կապերը մոդելավորող մաթեմատիկական օբյեկտներ են: Գրաֆը կազմված է «գագաթներից» (կամ «հանգույցներից») և «կողերից», որոնք միացնում են գագաթների որոշ զույգեր: |
||
| Տող 4. | Տող 5. | ||
Գրաֆների տեսության հիմնական հասկացությունների համար այցելեք [[Գրաֆների տեսության բառարան]]։ |
Գրաֆների տեսության հիմնական հասկացությունների համար այցելեք [[Գրաֆների տեսության բառարան]]։ |
||
{| align="center" |
|||
|----- |
|||
| [[Պատկեր:Complete graph K1.svg|100px]] |
|||
| [[Պատկեր:Complete graph K2.svg|100px]] |
|||
| [[Պատկեր:Complete graph K3.svg|100px]] |
|||
| [[Պատկեր:Complete graph K4.svg|100px]] |
|||
|----- |
|||
| [[Պատկեր:Complete graph K5.svg|100px]] |
|||
| [[Պատկեր:Complete graph K6.svg|100px]] |
|||
| [[Պատկեր:Complete graph K7.svg|100px]] |
|||
| [[Պատկեր:Complete graph K8.svg|100px]] |
|||
|----- |
|||
| colspan="4" align="center" | Մեկից ութ գագաթանի լրիվ գրաֆները․ <math>K_1...K_8</math>: |
|||
|} |
|||
==Սահմանումներ== |
==Սահմանումներ== |
||
10:49, 7 Դեկտեմբերի 2014-ի տարբերակ

Մաթեմատիկայում և համակարգչային գիտության մեջ գրաֆների տեսությունը ուսումնասիրում է գրաֆները, որոնք օբյեկտների միջև զույգ առ զույգ կապերը մոդելավորող մաթեմատիկական օբյեկտներ են: Գրաֆը կազմված է «գագաթներից» (կամ «հանգույցներից») և «կողերից», որոնք միացնում են գագաթների որոշ զույգեր:
Գրաֆը կարող է լինել չուղղորդված (չկողմնորոշված), երբ յուրաքանչյուր կողի երկու ծայրակետերը համարժեք են, կամ կողերը կարող են ուղղորդված (կողմնորոշված) լինել մի ծայրակետից մյուսը: Տես գրաֆներ հոդվածը ավելի մանրամասն սահմանումների համար։ Գրաֆները Դիսկրետ մաթեմատիկա բաժնում ուսումնասիրվող պարզագույն օբյեկտներից են։
Գրաֆների տեսության հիմնական հասկացությունների համար այցելեք Գրաֆների տեսության բառարան։
Սահմանումներ

Գրաֆը սահմանվում է որպես կարգավոր զույգ G=(V,E), որտեղ V-ն գագաթների (կամ հանգույցների) բազմությունն է, իսկ E-ն՝ կողերի (գծերի), որոնք V բազմության երկու տարրանոց ենթաբազմություններ են (այսինքն, կողը բնութագրվում է որպես երկու տարբեր գագաթների չկարգավորված զույգ): Գրականությունում հանդիպող այլ սահմանումներից տարբերելու համար այսպես սահմանվող գրաֆները երբեմն կոչում են չկողմնորոշված և հասարակ գրաֆներ:
Կողին պատկանող գագաթները կոչվում են այդ գագաթի ծայրակետեր: Հաճախ {u, v} կողը կրճատ նշանակում են uv-ով:
Երբեմն E բազմությունը սահմանվում է որպես (իրարից տարբեր) գագաթների չկարգավորված զույգերի մուլտիբազմություն: Այսպես սահմանվող օբյեկտները կոչվում են մուլտիգրաֆներ: Գագաթների միևնույն զույգի միջև մեկից ավելի կողերը կոչվում են պատիկ կողեր: Եթե թույլատրվում են նաև այնպիսի կողեր, որոնց երկու ծայրերն էլ միանում են միևնույն գագաթին (առաջացնելով օղակ), այդ դեպքում ասում են, որ գործ ունենք պսևդոգրաֆի հետ:
Սովորաբար V և E բազմությունները ընդունվում են վերջավոր: Հակառակ դեպքում գործ ունենք անվերջ գրաֆների հետ, որոնց համար վերջավոր գրաֆների բազմաթիվ հատկություններ տեղի չունեն: Գրաֆի կարգը գագաթների բազմության հզորությունն է: Որևէ գագաթի աստիճանը այդ գագաթին միացած կողերի քանակն է: Պսևդոգրաֆների դեպքում, երբ որևէ կողի երկու ծայրերն էլ միացած են միևնույն գագաթին, այդպիսի կողերը (օղակները) հաշվվում են երկու անգամ:
Կիրառություններ

Գրաֆները կիրառվում են ֆիզիկայի, քիմիայի, կենսաբանության, սոցիալական և ինֆորմացիոն համակարգերի մոդելավորման մեջ: Այս և այլ ուղղություններում բազմաթիվ խնդիրներ արդյունավետ կերպով լուծվում են գրաֆային ալգորիթմներով:
Համակարգչային գիտություններում գրաֆներով մոդելավորում են համակարգչային ցանցերը, տվյալների կառուցվածքները, հաշվարկի ընթացքը և այլն: Օրինակ, որպես գագաթների բազմություն կարելի է ընտրել ինտերնետային կայքերը, իսկ կայքերի միջև հղումները կդառնան ուղղորդված կողեր գագաթների միջև: Գրաֆների միջոցով ներկայացվող տվյալները արդյունավետ պահելու և կառավարելու համար գոյություն ունեն գրաֆային տվյալների հենքեր: Գրաֆների տեսությամբ են մոդելավորվում գերմեծ ինտեգրալ սխեմաների նախագծման ժամանակ առաջացող բազմաթիվ խնդիրներ (օրինակ՝ routing-ի խնդիրը):
Քիմիայում և պինդ մարմնի ֆիզիկայում գրաֆների միջոցով մոդելավորում են ատոմները և նրանց միջև կապերը:
Գրաֆների պատկերում

Գրաֆները հաճախ ներկայացվում են հարթության վրա պատկերի միջոցով: Յուրաքանչյուր գագաթի համար պատկերվում է կետ կամ շրջան, իսկ կողերը ներկայացվում են գագաթները միացնող կորերով: Ուղղորդված գրաֆների դեպքում կորերի մի ծայրում պատկերվում են սլաքներ:
Ակնհայտորեն, միևնույն գրաֆը կարելի է պատկերել տարբեր ձևերով, և ընդհանուր դեպքում դժվար է ճանաչել, թե երբ են տարբեր պատկերները համապատասխանում միևնույն գրաֆին: Գրաֆների գեղեցիկ կամ հարմար պատկերումը գրաֆների տեսության բարդագույն խնդիրներից է: Մշակված են մի շարք որակի չափանիշներ (կողերի հատումների թիվը, համաչափությունը, գագաթների հեռավորությունը իրենցով չանցնող կողերից և այլն), ինչպես նաև բազմաթիվ պատկերման ալգորիթմներ [2]:
Այն գրաֆները, որոնք հնարավոր է պատկերել հարթության վրա այնպես, որ կողերը չհատվեն, կոչվում են հարթ գրաֆներ: Եթե այդպիսի պատկերում հնարավոր չէ, ապա հատումների նվազագույն քանակը, որին կարելի է հասնել, կոչվում է գրաֆի խաչումների թիվ: Հարթ գրաֆների խաչումների թիվը հավասար է զրոյի: Հարթ գրաֆների հետազոտությունը, ինչպես նաև տրված գրաֆի խաչումների թիվը հաշվելը գրաֆների տեսության հայտնի խնդիրներից են:
Գրաֆների տեսության խնդիրներ
Ենթագրաֆներ, մինորներ
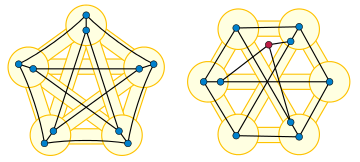
Գրաֆների տեսության հետաքրքիր խնդիրներից է ենթագրաֆների իզոմորֆիզմի խնդիրը, երբ տրված գրաֆում անհրաժեշտ է պարզել որոշակի ենթագրաֆի գոյությունը: Այս խնդիրները կարևորվում են այն պատճառով, որ գրաֆների բազմաթիվ հատկանիշներ (հարթ լինելը, երկկողմանի լինելը և այլն) ժառանգական են ենթագրաֆների նկատմամբ, այսինքն տրված գրաֆը բավարարում է այդ հատկությանը այն և միայն այն դեպքում, երբ նրա բոլոր ենթագրաֆները ևս բավարարում են նույն հատկությանը: Սակայն, որոշակի ենթագրաֆների գոյությունը պարզելը հաճախ բարդ խնդիր է: Մասնավորապես, տրված գրաֆում ամենամեծ լրիվ գրաֆ ենթագրաֆի գտնելը NP-լրիվ խնդիր է[3]:
Նման խնդիրներ դրվում են նաև ծնված ենթագրաֆների համար: Այս խնդիրներն էլ հաճախ բարդ են: Օրինակ, տրված գրաֆում մեծագույն անկախ բազմություն գտնելու խնդիրը (այսինքն, մեկուսացված գագաթներով ծնված ենթագրաֆ գտնելը) նույնպես NP-լրիվ է:
Հայտնի խնդիր է տրված գրաֆում որոշակի մինորների գոյության հարցը: H գրաֆը կոչվում է G գրաֆի մինոր, եթե այն ստացվում է G-ից գագաթներ և կողեր հեռացնելով, ինչպես նաև կողեր կծկելով: Գրաֆների շատ հատկանիշներ ժառանգական են մինորների նկատմամբ, որոնցից թերևս ամենահայտնին գրաֆի հարթ լինելու պայմանն է: Վագների թեորեմը պնդում է, որ գրաֆը հարթ է այն և միայն դեպքում, երբ այն չի պարունակում K3,3 լրիվ երկկողմանի գրաֆը և K5 լրիվ գրաֆը որպես մինոր:
Գրաֆների ներկումներ

Գրաֆների տեսության բազմաթիվ խնդիրներում գրաֆի տարբեր տարրերին (կող, գագաթ և այլն) համապատասխանեցվում են գույներ կամ թվեր: Այդպիսի արտապատկերումները գրաֆի տարրերից թվերին կոչվում են ներկումներ:
Գագաթային ներկումներ
Ճիշտ գագաթային ներկման դեպքում գագաթներին համապատասխանեցվում են գույներ (թվեր) այնպես, որ հարևան գագաթների գույները լինեն տարբեր: Ակնհայտորեն, բոլոր գրաֆները ունեն այդպիսի ներկումներ, քանի որ կարելի է ամեն գագաթին համապատասխանեցնել մի նոր գույն: Սակայն խնդիր է առաջանում գտնել գույների ամենափոքր թիվը, որոնցով կարելի է ապահովել ճիշտ գագաթային ներկում: Այդ թիվը կոչվում է գրաֆի քրոմատիկ թիվ: Դրա որոշումը NP-լրիվ խնդիր է[4], սակայն հայտնի են բազմաթիվ գնահատականներ: Օրինակ, ըստ Բրուքսի թեորեմի [5], գրաֆի քրոմատիկ թիվը չի գերազանցում գրաֆի առավելագույն աստիճանը, բացառությամբ ցիկլերի և լրիվ գրաֆների:

Հարթ գրաֆների դեպքում քրոմատիկ թիվը գտնելու խնդիրը հայտնի է որպես քարտեզ ներկելու խնդիր: Եթե երկրներին (կամ ցանկացած տարածքային միավորին) համպատախասնեցվեն գագաթներ հարթության վրա, իսկ հարևան երկրները միացվեն կողերով, ապա ճիշտ գագաթների ներկումը կհամապատասխանի քարտեզի ներկմանը: Չորս գույների թեորեմի համաձայն, հարթ գրաֆի քրոմատիկ թիվը չորսից մեծ չէ, հետևաբար ցանկացած քարտեզ ներկելու համար բավարար է օգտագործել չորս գույն:
Ճիշտ գագաթային ներկումների հայտնի չլուծված խնդիրներից է Հադվիգերի հիպոթեզը, ըստ որի k քրոմատիկ թիվ ունեցող գրաֆը պետք է պարունակի k-գագաթանի լրիվ գրաֆը որպես մինոր: Այս հիպոթեզը չորս գույների թեորեմի ընդհանրացումն է:
Կողային ներկումներ
Երբ գագաթների փոխարեն ներկվում են կողերը և պահանջ է դրվում, որ կից կողերը ունենան տարբեր գույներ, այդպիսի ներկումը կոչվում է ճիշտ կողային ներկում: Ճիշտ կողային ներկման դեպքում նվազագույն գույների քանակը կոչվում է գրաֆի քրոմատիկ դաս, որը հաշվելը ևս NP-լրիվ խնդիր է: Վիզինգի թեորեմի համաձայն, քրոմատիկ դասը կարող է հավասար լինել գրաֆի առավելագույն աստիճանին, կամ դրանից մեծ լինել ճիշտ մեկով:
Գրաֆի ճիշտ կողային ներկումը համարժեք է գրաֆի կողային գրաֆի ճիշտ գագաթային ներկմանը:
Ինչպես գագաթային, այնպես էլ կողային ներկումների համար սահմանվում են ցուցակային ներկումներ, երբ յուրաքանչյուր գագաթի (կողի) համապատասխանեցվում է գույների ցուցակ, որտեղից անհրաժեշտ է ընտրել գույներ այնպես, որ ստացված ներկումը լինի ճիշտ: Կողային ցուցակային ներկման հիպոթեզի համաձայն, ցանկացած օղակ չպարունակող մուլտիգրաֆի համար կողային ցուցակային քրոմատիկ թիվը պետք է հավասար լինի գրաֆի քրոմատիկ դասին: Այս խնդիրը ևս լուծված չէ [6]:
Տոտալ ներկումներ
Ներկումը կոչվում է տոտալ, երբ ներկվում են ինչպես գագաթները, այնպես էլ կողերը: Այս ոլորտի ամենահայտնի խնդիրը տոտալ ներկման հիպոթեզն է, որը ձևակերպվել է Վիզինգի և Բեհզադի կողմից 1965թ․ և մինչ այժմ լուծված չէ [7]:
Ծանոթագրություններ
- ↑ Scott Hale, Multilinguals and Wikipedia Editing, 2013 [1]
- ↑ Գրաֆների պատկերում (անգլերեն)
- ↑ Մեծագույն լրիվ ենթագրաֆի հզորությունը կոչվում է clique number: Ավելի մանրամասն՝ Wolfram MathWorld: Clique Number
- ↑ Քրոմատիկ թվի մասին Wolfram MathWorld-ում
- ↑ Բրուքսի թեորեմը Wolfram MathWorld-ում
- ↑ Կողային ցուցակային ներկման հիպոթեզը Open Problem Garden-ում
- ↑ Տոտալ ներկման հիպոթեզը Open Problem Garden-ում
| Վիքիպահեստ նախագծում կարող եք այս նյութի վերաբերյալ հավելյալ պատկերազարդում գտնել Գրաֆների տեսություն կատեգորիայում։ |

