Մասնակից:Narine Man/Ավազարկղ

Միջին մակերևույթային ջերմաստիճանը 1961 թվականից մինչև 1990 թվականը

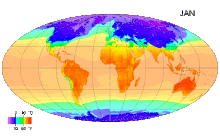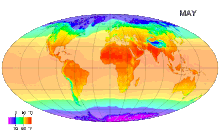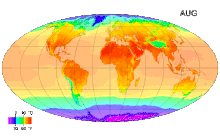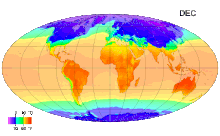
Ջերմաստիճան (լատ. temperatura - պատշաճ խառնուրդ, նորմալ վիճակ,) ֆիզիկական մեծություն, որը բնութագրում է թերմոդինամիկական համակարգը  և աստիճանաբար արտահայտում է մարմնի տարբեր աստիճանի ջերմության ներըմբռնումհասկացությունը:

Կենդանի օրգանիզմները կարող են ուղակիորեն ջերմության և սառնության զգացողությունները զգալ զգայարանների միջոցով: Այնուամենայնիվ, ջերմաստիճանի ճշգրիտ որոշումը պահանջում է, որ ջերմաստիճանը չափվի օբյեկտիվորեն օգտագործելով որոշակի գործիքներ: Նման սարքերը կոչվում են ջերմաչափեր և չափում են այսպես կոչված էմպիրիկ ջերմաստիճանը: Էմպիրիկ սանդղակով ջերմաստիճանը որոշվում է 2 հիմնարար կետերի միջև եղած ստորաբաժանումների քանակով, այդպես են ստեղծված կիրառվող Ցելսյուսի սանդղակը, ֆարենհայտի և ուրիշների սանդղակները: Կելվինի սանդղակով ջերմաստիճանը որոշվում է մեկ հիմակետի միջոցով հաշվի առնելով այն հանգամանքը,որ բնության մեջ կա մի նվազագույն սահմանաչափ՝ բացարձակ զրո: Վերին ջերմաստիճանը սահմանափակում է Պլանկի ջերմաստիճանը:

Եթե համակարգը գտնվում է ջերմային հավասարակշռության մեջ, ապա նրա բոլոր մասերի ջերմությունը նույնն է: Հակառակ դեպքում համակարում էներգիան փոխանցվում է ավելի ջեռուցված մասերից դեպի ավելի քիչ ջերմացնող մասերը, ինչը հանգեցնում է ջերմաստիճանի հավասարեցմանը համակարգում և նրանք համապատասխանում են ջերմաստիճանի բաշխման համակարգում կամ ջերմաստիճանի սկալյար դաշտում: Ջերմադինամիկայում ջերմաստիճանը ինտենսիվ թերմոդինամիկ մեծություն է:

Թերմոդինամիկայի հետ մեկտեղ, ֆիզիկայի այլ բաժիններում կարող են ներկայացվել ջերմաստիճանի որոշման այլ եղանակներ: Մոլեկուլային-կինետիկ տեսությունում ցույց է տրված, որ ջերմաստիճանը համամասնական է համակարգի մասնիկների միջին քանակային էներգիային: Ջերմաստիճանը որոշում է մասնիկների բաշխումը էներգետիկ համակարգի մակարդակներում (տե՛ս Մաքսվել- Բոլցմանի վիճակագրություն), մասնիկների բաշխման արագությունները (Տես, Մաքսվելի բաշխումը), իոնացման աստիճանը (տես, Սախայի հավասարում), արտանետումների սպեկտրային խտությունը (տես Պլանկի ճառագայթման օրենք), ամբողջական ճառագայթման խտությունը (տես, Ստեֆան-Բոլցմանի օրենք) և այլն: Բոլցմանի բաշխման պարամետրերի մեջ մտնող ջերմաստիճանները հաճախ կոչվում են շարժման ջերմաստիճան, Սահայի բանաձևը՝ իոնացման ջերմաստիճան և Ստեֆանի- Բոլցմանի օրենքը՝ ճառագայթային ջերմաստիճան: Թերմոդինամիկ հավասարակշռության համակարգում այս բոլոր պարամետրերը հավասար են միմյանց և կոչվում են պարզապես ջերմաստիճանային համակարգ:

Միջազգային միավորների համակարգում (անգլ. International System of Quantities, ISQ) ջերմաստիճանը ընտովեւմ է, որպես համակարգի յոթ հիմնական ֆիզիկական մեծություններից մեկը: Միավորների միջազգային համակարգում (SI) Կելվինի ջերմաստիճանը համարվում է յոթ հիմանական սորաբաժանումներից մեկը SI : SI համակարգում եւ գործնականում կիրառվում ևնաեւ Ցելսիուսի ջերմաստիճանը, որի միավորը Ցելսիուսի սանդղակում (° C) աստիճանն է, հավասար է Կել ինին: Սա հարմար է, քանի որ Երկրի կլիմայական առավելագույն գործընթացները ընթանում են բնական պայմաններում, -50-ից +50 °C-ի պայմաններում:

Միջին մակերևույթային ջերմաստիճանը 1961 թվականից մինչև 1990 թվականը

Ջերմաստիճանը որպես տեղական պարամետր: Ջերմաստիճանային դաշտ:

Խտացված նյութի ֆիզիկական ջերմաստիճանը դիտարկում են, որպես տեղային մակրոսկոպիկ փոփոխական, այսինքն, շրջակա միջավայրի մոտավոր հատկացված տարածքի տարրական ծավալը բնութագրող արժեքը,որի չափերը անսահման փոքր է քան միջավայրի անհամապատասխանությունները և անսահմանորեն մեծ են միջավայրի մասնիկների (ատոմներ, իոնների, մոլեկուլներ և այլն) չափերից: Ջերմաստիճանը կարող է փոփոխվել մի կետից մյուսը (մեկ տարրական ծավալից մյուսը ), տիեզերքում ջերմաստիճանի որոշումը տվյալ ժամանակում կատարվում է սկալյարային դաշտով (ջերմաստիճանի դաշտ ):

Ջերմաստիճանային դաշտը կարող է լինել անկայուն (ժամանակի ընթացքում փոփոխվող), և կախված չէ ժամանակի կայունությունից: Միևնույն ջերմաստիճանի արժեքն ունեցող միջավայրը բոլոր կետերում համարվում է ջերմայինորեն համասեռ: Մաթեմատիկական առումով, ջերմաստիճանը բնութագրվում է ջերմաստիճանի կախվածության հավասարման միջոցով  T՝ տարածական կոորդինատներով (Երբեմն դիտարկում են մեկ կամ երկու կոորդինատներ) և ժամանակով: Ջերմային համասեռ համակարգերի համար, T=0:

Թերմոդինամիկ սահմանումը

Թերմոդինամիկ մոտեցման պատմություն

«Ջերմաստիճան» բառը ծագեց այն օրերին, երբ մարդիկ հավատում էին, որ ավելի շատ ջերմային մարմիններում կա ավելի շատ հատուկ նյութ`ջերմություն, քան ավելի քիչ ջերմացվում է: Հետեւաբար, ջերմաստիճանը ընկալվեց որպես մարմնի և ջերմության խառնուրդի ուժ: Այդ պատճառով ալկոհոլի և ջերմաստիճանի ուժեղ միավորները կոչվում են նույն աստիճաններ:

Ջերմադինամիկական հավասարակշռության պայմաններում ջերմաստիճանը նույն արժեքն ունի համակարգի բոլոր մակրոսկոպիկ մասերի համար: Եթե երկու մարմիններն ունեն նույն ջերմաստիճանը համակարգում, ապա մասնիկների կինետիկ էներգիան (ջերմաքանակ)նրանց մևեւ չի փոխանցվում: Եթե կա ջերմաստիճանի տարբերություն, ապա ջերմության փոխանցումը տեղի է ունենում ավելի բարձր ջերմաստիճանի մարմնից դեպի ավելի ցածր ջերմաստիճանի մարմնը:

Ջերմությունը նույնպես կապված է ջերմության և ցրտի զգացողության հետ, այսինքն կապված կենդանի հյուսվածքից ստանում է ջերմություն կամ տալիս է այն:

Որոշ քվանտային մեխանիկական համակարգեր (օրինակ, լազերային աշխատանքային մարմինը, որտեղ առկա են ներկառուցված մակարդակները) կարող է լինել այնպիսի պետությունում, որտեղ էնտրոպիան չի աճում, բայց նվազում է էներգիայի ավելացման հետ, որը պաշտոնապես համապատասխանում է բացասական բացարձակ ջերմաստիճանի: Այնուամենայնիվ այսպիսի վիճակը գտնվում է «բացարձակ զրոյից ցածր», բայև«վերեւում անսահմանություն», քանի որ այս համակարգի շփումը մաշկի հետ է ջերմային էներգիան փոխանցբում է համակարգից մարմնին, բայց հակառակը տեղի չի ունենում (տես, բացարձակ ջերմաստիճանը):

Ջերմաստիճանի հատկությունները ուսումնասիրվում են ֆիզիկայի բաժնում`թերմոդինամիկայում: Ջերմաստիճանը նույնպես կարևոր դեր է խաղում գիտության բազմաթիվ ոլորտներում, այդ թվում` ֆիզիկայի այլ ճյուղերում, ինչպես նաև քիմիայում և կենսաբանությունում:

Հավասարակշռված և անհավասարակշռված ջերմաստիճան

Թերմոդինամիկական համակարգը, որը գտնվում է թերմոդինամիկական համակարգի հավասարակշռության վիճակում, ունի կայուն ջերմաստիճանի դաշտ: Եթե ​​նման համակարգում գոյություն չունեն ադիաբատիկ (էներգակիրային) բաժանմունքներ, ապա համակարգի բոլոր մասերը նույն ջերմաստիճանը ունեն: Այլ կերպ ասած, ջերմային համասեռ համակարգի հավասարակշռման ջերմաստիճանն անմիջապես կախված չէ կախվածությունից (բայց կարող է տարբեր լինել քվազի-ստատիկ գործընթացներում): Ընդհանուր գործողության մեջ անհավատարմային համակարգ ունի ոչ կայուն ջերմաստիճանի դաշտ, որի միջավայրի յուրաքանչյուր տարրական ծավալը ունի իր անհավասարակշռող ջերմաստիճանը, որը կախված է իր ժամանակից:

Ֆենոմենոլոգիական թերմոդինամիկայի ջերմաստիճան

Ֆենոմենոլոգիական ջերմոդինամիկայում ջերմաստիճանի որոշումը կախված է տվյալ կարգի մաթեմատիկական ապարատի կառուցվածքի մեթոդից (տես,Թերմոդինամիկայի ակսիոմատիկա):

Ֆենոմենոլոգիական թերմոդինամիկայում ջերմաստիճանը կախված է մաթեմատիկական ապարատի կառուցումով (տես Թերմոդինամիկայի ակսիոմատիկա):Թերմոդինամիկական ջերմաստիճանի սահմանումների տարբերությունները տարբեր համակարգերում թերմոդինամիկայի կառուցումը չի ենթադրում ավելի մեծ տեսանելիություն որոշ նման համակարգերի համեմատ,բոլոր այդ համակարգերում առաջին հերթին ջերմաստիճանը նկարագրելու համար դիտարկվում է տաքացվածության աստիճանը/մարմնի սառեցմանը, և երկրորդ իմաստալից սահմանումը, որը ստեղծում է կապ թերմոդինամիկական ջերմաստիճանի և նրա չափման համար կիրառվող ջերմաստիճանները համնկնում են:

Ռացիոնալ թերմոդինամիկայում առաջին հերթին հրաժարվելով այդ կարգու կանոնից բաժանվում են թերմոդինամիկական հավասարակշռության և թերմոդինամիկական անհավասարակշռության մեջ (այսինքն, չկատարելու հավասարակշռությաևեւ հավասարակշռության ջերմաստիճանների մևեւ տարբերություն), ջերմաստիճանը նախնական չճանաչելի փոփոխական է, նկարագրվում են միայն այն հատկություններով, որոնք կարող են արտահայտվել մաթեմատիկայի լեովվ: ով Էներգիայի, ջերմության, էնտրոպիական և քիմիական պոտենցիալ հասկացությունները ռացիոնալ թերմոդինամիկայում ներկայացվում են միաժամանակ. սկզբունքորեն նրանք անհատապես չեն կարող որոշվել:  Այս հասկացությունների ներդրման մեթոդը ցույց է տալիս, որ հաշվի են առնվում տարբեր էներգետիկ հոսքերին համապատասխանող տարբեր ջերմաստիճանները: Օրինակ, մենք կարող ենք ներկայացնել տրանսֆորմացիոն և սպինորային ջերմաստիճաններով, ճառագաայիլ|ջերմաստիճանին և այլն։

Զրոյական սկիզբը (օրենքը) ներկայացնում է թերմոդինամիկական հավասարակշռման էմպիրիկական ջերմաստիճանի հասկացթյոււ նը , որպես պետությունների պարամետր, որի բոլոր կետերում հավասարությունը ջերմային հավասարակշռության պայման է առանց համակարգային բաժանման առանցքային համակարգում:

Ռ.Կ Կլաուզիուսի հևեւորդների կողմից օգտագործվող տերմոդինամիկայի կառուցման մոտեցման մեջ հավասարակշռության պարամետրերը`տերմոդինամիկային ջերմաստիճանը T- ն եւ էնտրոպիան S- ը որոշում են թերմոդինամիկային պարամետրը:

$\delta Q=TdS,$

(Թերմոդինամիկական ջերմաստիճանը և էնտրոպիան, ըստ Կլաուզիուսի)

որտեղ $\delta Q$- ն տարրական (անսահմանափակ) հավասարակշռման գործընթացում ստացված կամ տրամադրված ջերմության քանակն է փակ համակարգում: Ավելին, ըստ Կլաուզիուսի համաձայն ջերմոդինամիկ ջերմաստիճանի հասկացությունը տարածվում է բաց համակարգերի և օրենքների շարքում լրացուցիչ ակիոմներ ներառելու հարցը:

Կարատեոդիալ ակսիոմատիկայում $\delta Q$- ն համարվում է, որպես դիֆերենցիալ Պֆաֆֆյան ձև, իսկ հավասարակշռության թերմոդինամիկ ջերմաստիճանը, որպես այս դիֆերենցիալ ձևի ինտեգրող բաժանարար :

Ա.Ա. Գուխմանի ակսիոմաների համակարգում $U$ համակարգի ներքին էներգիայի փոփոխությունը տարրական հավասարակշռության գործընթացում արտահայտվում է փոխգործակցության ներուժով՝ $P_{k}$, և պետական կոորդինատներով՝ $x_{k}$:

$dU=\sum _{k}P_{k}dx_{k},$

(Գուխմանի հավասարում)

Ջերմային ներուժը հանդիսանում է թերմոդինամիկական ջերմաստիճանը $T$, իսկ ջերմային կոորդինատը՝ էնտրոպիան՝ $S$. ճնշումը (հակառակ նշանով) դեր է խաղում մեխանիկական դեֆորմացիայի փոխազդեցության ներդաշնակության, հեղուկների և գազերի ներգործության համար, և ճնշման ծավալը համադրում է որպես ծավալ: քիմիական և փուլային անցումների համար պետական ​​կոորդինատներն ու պոտենցիալները, և դրանց հետ կապված քիմիական ներուժը բաղադրիչների զանգվածներն են: Այլ կերպ ասած, Գուխմանի ակսիոմատիկայում, ըստ Գիբբսի հավասարման թերմոդինամիկայում ջերմաստիճանը և քիմիական պոտենցիալները հավասարապես հավասարակշռում են: Օգտագործվում է Գուխմանի և նրա հետեւորդների կողմից առաջարկված պետական համակարգը, որը երկրաչափական, մեխանիկակաևեւ էլեկտրամագնիսական փոփոխականներից բացի իր մեջ ներառում է տարրերի էնտրոպիան և զանգվածը, և բացառում է ընդհանրացված թերմոդինամիկական կոորդինատների հետ կապված երկիմաստությունը. Որոշ հեղինակներ առնչվում են ընդհանրացված համակարգերի փոփոխականներին՝ Էնտրոպիաին և զանգվածին, իսկ մյուսները սահմանափակվում են երկրաչափական, մեխանիկական և էլեկտրամագնիսական փոփոխականներով:

Գիբբսի թերմոդինամիկայում հավասարակշռության ջերմաստիճանը արտահայտվում է ներքին էներգիայով և էնտրոպիայով:

$T\equiv \left({\frac {\partial U}{\partial S}}\right)_{\{x_{i}\}},$

(Թերմոդինամիկական ջերմաստիճանը, ըստ Գիբսի)

որտեղ ${\{x_{i}\}}$-ն ներքին էներգիայի բնական փոփոխականների (առանց էնտրոպիա) սահմանումն է, որպես բնորոշ գործընթաց: Համակարգի բոլոր կետերում ջերմաստիճանի հավասարությունը, առանց ադրբիատիկ ճնշման, որպես Գիբսսի թերմոդինամիկային ջերմային հավասարակշռության պայման, բխում է ներքին էներգիայի հատկություններից և թերմոդինամիկ հավասարակշռության վիճակում գտնվող էնթրոպիայից:

Ֆալկի եւ Յունգի ակսիոմատիկան, էնտրոպիայի որոշման ժամանակ, չի զիջում հավասարակշռության և հավասարակշռված պետությունների միջև, և, հետեւաբար, այս համակարգում տեղադրված ջերմաստիճանի և ներքին էներգիայի սահմանման համար ջերմաստիճանի սահմանումը հավասարապես կիրառելի է ցանկացած ջերմային համասեռ համակարգերի համար.

$T\equiv \left[\left({\frac {\partial S}{\partial U}}\right)_{\{x_{i}\}}\right]^{-1},$

(Թերմոդինամիկական ջերմաստիճանը, ըստ Ֆալկի և Յունգի)

որտեղ ${\{x_{i}\}}$-ն անկախ էնտրոպիայի փոփոխականների սահմանն է (որը չի պարունակում ներքին էներգիա):

Լոկալ հավասարակշռության սկզբունքը թույլ է տալիս ոչ հավասարակշռված համակարգերին փոխարինել ջերմաստիճանի սահմանումը հավասարակշռության տերմոդինամիկայից եւ օգտագործել այս փոփոխականը, որպես միջավայրի տարրական ծավալի անխափան ջերմաստիճան.:

Լոկալ անհավասարակշռության սկզբունքի մերժման հիման վրա ընդլայնված տատանումային տերմոդինամիկայի (RNT) պայմաններում անհավասարակշռող ջերմաստիճանը տրվում է Ֆալկի և  Յունգի ակսիոմատկայի (տես Ֆալկի և  Յունգի Թերմոդինամիկ ջերմաստիճան) օգտագործման հետ կապված հարաբերության հետ, այլ ընդարձակ մուտանտի տարբեր փոփոխականների հետ: Գիբսի տեղական հավասարակշռված ջերմաստիճանի պայմաններում տարբերում են նաև RNT- ի անհավասարակշռված ջերմաստիճանի ընտրությամբ կախված էնտրոպիայի փոփոխությունից :

Ն. Ի. Բելոկոնի  ակսիոմատիկայում ջերմաստիճանի նախնական որոշումը հետևում է Բելոկոնի պոստուլից, որը կրում է հետևյալ անվանումը՝ ջերմաքանակի երկրորդ սկզբունքի պոստուլիտը: Ջերմաստիճանը մարմինների վիճակի միակ գործառույթն է, որը որոշում է այդ մարմինների միջև ինքնաբուխ ջերմության փոխանակման ուղղությունը, այսինքն` ջերմային հավասարակշռության մարմինները նույն ջերմաստիճանը ունեն ցանկացած ջերմաստիճանի մասշտաբով: Հևեւաբար, երկու մարմինները, որոնք չունեն ջերմային կոնտակտներ միմյանց հետ, սակայն նրանցից յուրաքանչյուրը ջերմային հավասարման մեջ երրորդի (չափիչ սարքի) հետ, ապա ունեն նույն ջերմաստիճանը:

Էմպիրիկական, բացարձակ և թերմոդինամիկ ջերմաստիճան

Ջերմաստիճանը չի կարող ուղղակիորեն չափվել: Ջերմաստիճանի փոփոխությունները գնահատվում են մարմնի այլ ֆիզիկական հատկությունների փոփոխություններով (ծավալ, ճնշում, էլեկտրական դիմադրություն, ճառագայթման ինտենսիվություևեւ այլն), որը միանգամայն կապված է դրա հետ (այսպես կոչված, ջերմաչափական հատկություններ): Քանակականորեն, ջերմաստիճանը որոշվում է`ցույց տալով, թե ինչպես է այն չափվում ջերմաչափով: Նման որոշումը չի ամրագրում կամ հաշվետվության սկիզբը կամ ջերմաստիճանի միավորի չափումը, այնպես որ ջերմաստիճանի չափման ցանկացած մեթոդ կապված է ջերմաստիճանային ցուցիչի ընտրության հետ: Էմպիրիկական ջերմաստիճանը  չափվում է ընտրված ջերմաստիճանում:

Թերմոդինամիկ ջերմաստիճանի որոշման ֆենոմենոլոգիական թերմոդինամիկան  կախված չի չափման համար օգտագործվող ջերմաչափային գույքի ընտրությունից: Ջերմաստիճանի փոփոխությունը  սահմանվում է թերմոդինամիկական ջերմաստիճանային սանդղակի օգնությամբ:

Թերմոդինամիկայում, որպես ակսիոմ, ենթադրությունը հիմնված է այն փորձի վրա, որ հավասարակշռության թերմոդինամիկ ջերմաստիճանը քանակական էբոլոր միակողմանի համակարգերի համար, ինչպես նաև ջերմաստիճանը համապատասխան այս ինտերֆեյսի նույնն է բոլոր թերմոդինամիկական համակարգերի համար, հետեւաբար, կարող է օգտագործվել որպես բնական ստուգիչ տվյալկետում ջերմաստիճանի ստուգման համար:Եթե ​տվյալ կետում ջերմաստիճանը զրոյական արժեք ունի է ջերմաստիճանի, ապա ջերմաստիճանային սանդղակի հիման վրա նույն տեղեկանքում միշտ կունենա նույն նշանը: Երկրորդ կետին դրական ջերմաստիճանի արժեքը սահմանելով` դրական ջերմաստիճանի բացարձակ ջերմաստիճան է տրվում, բացարձակ զրոյից չափվող ջերմաստիճանը կոչվում է բացարձակ ջերմաստիճան: Հետեւաբար, բացարձակ զրոյից չափվող թերմոդինամիկ ջերմաստիճանը կոչվում է բացարձակ թերմոդինամիկական ջերմաստիճան (տես, Կելվինի ջերմաստիճանը): Բացարձակ զրոյից ջերմաստիճանի ընթերցմամբ էմպիրիկ ջերմաստիճանի օրինակ է միջազգային գործնական ջերմաստիճանի մասշտաբը:

Ցելսիուսի ջերմաստիճանի մասշտաբը բացարձակ չէ:

Բացարձակ ջերմաստիճանի որոշումը որոշ հեղինակների կարծիքով կախված չէ բացարձակ զրոյից, այլ կախված է ջերմաստիճանային ցուցնակներից և չափման համար օգտագործվող ջերմաչափային գույքի ընտրությունից:

Բացասական բացարձակ ջերմաստիճանները

Հիմնական հոդված՝ Բացասական բացարձակ ջերմաստիճանները

Հավասարակշռված թերմոդինամիկ բացարձակ ջերմաստիճանը միշտ դրական է (տես էմպիրիկ, բացարձակ և թերմոդինամիկական ջերմաստիճանները): Բացասական ( Կելվինի մասշտաբով) ջերմաստիճանի օգտագործումը հարմար մաթեմատիկական մեթոդ է, որը հատուկ է առանձնահատկություններ ունեցող անհավասարակշիռ համակարգերը նկարագրելու համար : Այս մեթոդը բաղկացած է մտավոր բաժանման մեջ ֆիզիկական համակարգի մի մասնիկ ունեցող առանձնահատկություններ ունեցող օբյեկտների անկախ ենթահամակարգերից և ձեռք բերված մասնակի ենթահամակարգի առանձին հետազոտություններից: Այլ կերպ ասած, տիեզերքի նույն ծավալը համարվում է միաժամանակ զբաղված երկու կամ ավելի մասնակի ենթահամակարգերի կողմից, որոնք միմյանց հետ խոցելի են: Այս մոտեցման օրինակ է մագնիսական դաշտում բյուրեղի միջուկային պտույտների դիտարկումը, որը կախված է թույլ բյուրեղյա վանդակի ջերմային թրթռումներից: Եթե ​​մագնիսական դաշտի ուղղությունը արագ փոխվում է, երբ սպիններըիեն կարողանում փոփոխել դաշտը, միջուկային պտույտների համակարգը միաժամանակ կունենա բացասական անհավասարակշռության ջերմաստիճան , այսինքն, այս տեսանկյունից ներկայիս նույն տարածական տարածաշրջանում կլինեն երկու զուգահեռ փոխազդող համակարգեր տարբեր ջերմաստիճաններով : Շնորհիվ փոխազդեցության, երկու համակարգերի ջերմաստիճանը  որոշ ժամանակ անց հավասարվում է:

Դասական ֆենոմենոլոգիական տերմոդինամիկայի ֆորմալիզմը կարելի է համալրել բացասական բացարձակ ջերմաստիճանների ներկայացմամբ :

  Տեսիի պոստուլին համապատասխան, ցանկացած համակարգի ներքին էներգիան սահմանափակվում է նվազագույնից, և այս սահմանը համապատասխանում է բացարձակ զրոյական ջերմաստիճանին : Համակարգերում, որոնք ունեն ոչ միայն ստորին, այլև ներքին էներգիայի վերին սահման, ջերմաստիճանը մեծանալով ներքին էներգիան ավելանում է և հասնում է իր սահմանային արժեքին. $T$ ջերմաստիճանի հետագա աճը չի հանգեցնում ներքին էներգիայի ավելացմանը, այլեւ $S$ համակարգի իջեցմանը $S\rightarrow 0$-ից $T\rightarrow -0$ : Թերմոդինամիկական բանաձևերի համաձայն, դա համապատասխանում է դրական ջերմաստիճանի շրջանից անցում դեպի բացասական ջերմաստիճան $\pm \infty$ ( $T=+\infty$ և $T=-\infty$ ջերմաստիճանները ֆիզիկապես նույնական են) հավասարաչափ ջերմաստիճանի սահմանով կետի ուղղությունը $-0$ :

Մոլեկուլային-կինետիկ հասկացությունը

Մոլեկուլային-կինետիկ տեսության մեջ ջերմաստիճանը սահմանվում է որպես մակրոսկոպիկական համակարգի մասնիկների միջին քննակականն էներգիայի բնութագիր, որը գտնվում է թերմոդինամիկ հավասարակշռության վիճակում մի աստիճանի ազատության վրա:

«... ջերմաստիճանի չափը շարժումը չէ, այլ շարժման պատահականությունը: Մարմնի քաոսային վիճակը սահմանում է իր ջերմաստիճանը և այդ գաղափարը (որն առաջին անգամ մշակել է Բոլցմանը), որ մարմնի որոշակի ջերմաստիճանի վիճակն ամենևին էլ չի որոշվում շարժման էներգիայով, այլ այս շարժման քաոսային բնույթով և այն նոր հայեցակարգ է, որը նկարագրում է ջերմային երեւույթները, որոնք մենք պետք է օգտագործենք ...

Պ.Լ. Կապիցա |

Վիճակագրական ֆիզիկայի ջերմաստիճանի որոշում

Վիճակագրական ֆիզիկայի մեջ ջերմաստիճանը որոշվում է որպես համակարգային էներգիայի ածանցյալ իր էնտրոպիայից

$T={\frac {dE}{dS}}$

որտեղ $S$-ը էնտրոպիան է, $E$-ն ջերմատունկի էներգիան է: Աև ձեւով ներկայացված քանակությունը $T$ նույնն է տարբեր մարմինների համար`թերմոդինամիկ հավասարակշռության ներքո: Երբ երկու մեծ արժեքով $T$ մարմինները շփվում են մեկը մյուսին էներգիա է տալիս:

Ջերմաստիճանի չափում

Հիմնական հոդված՝ Ջերմաչափ

Թերմոդինամիկ ջերմաստիճանը չափելու համար ընտրվում է ջերմաչափային նյութի որոշակի թերմոդինամիկ պարամետր: Այս պարամետրի փոփոխությունը բացառապես կապված է ջերմաստիճանի փոփոխության հետ: Թերմոդինամիկ ջերմաչափի դասական օրինակ կարող է հանդիսանալ գազայինի ջերմաչափը, որի ջերմաստիճանը որոշվում է մշտական գոլորշիով գազի ճնշումը չափելու մեթոդով: Հայտնենե ւ բացարձակ ճառագայթման ջերմաչափեր, աղմուկևեւ ակուստիկ ջերմաչափեր:

Թերմոդինամիկ ջերմաչափերը շատ բարդ կառուցվածքներ են, որոնք չեն կարող օգտագործվել գործնական նպատակների համար: Հետևաբար, չափումների մեծ մասը կատարվում է պրակտիկ ջերմաչափերով, որոնք երկրորդական են, քանի որ դրանք չեն կարող ուղղակիորեն չափել որոշակի նյութերի ջերմաստիճանը: Ինտերպոլիֆիկացման գործառույթը ձեռք բերելու համար դրանք պետք է ստուգեն միջազգային ջերմաստիճանը հիմնական կետերում:

Մարմնի ջերմաստիճանը չափելու համար սովորաբար չափվում է ցանկացած ֆիզիկական պարամետր, որը կապված է ջերմաստիճանի հետ, օրինակ, գազերի համար երկրաչափական չափերը (տես, դիլատոմետր) ծավալը կամ ճնշումը, ձայնի արագությունը, էլեկտրական հաղորդունակությունը, էլեկտրամագնիսական կլանումը կամ ճառագայթման սպեկտրը (օրինակ, պիրոմետրերը, ֆոտոսֆերայի ջերմաստիճանի չափումը և մթնոլորտում աստղերի ճնշումը, վերջին դեպքում դոպլեր ընդլայնումը  սպեկտրալ գծերի կլանումը կամ ճառագայթումը):

Ամենօրյա պրակտիկայում ջերմաստիճանը սովորաբար չափվում է հատուկ գործիքներով՝ կոնտակտային ջերմաչափերո վ:Այս դեպքում ջերմաչափը հաստատում է ջերմային կապ ուսումնասիրվող մարմնի հետ և ջերմաչափը մարմնի թերմոդինամիկ հավասարակշռությունը  հաստատելուց հետո,  հավասարեցնում է ջերմաստիճանը, կախված ջերմաչափի ֆիզիկական հատկություններից: Թերմոմետրի և մարմնի մևեւ ջերմային կոնտակտը պետք է լինի բավարար, որպեսզի ջերմաստիճանի հավասարությունը տեղի ունենա ավելի արագ, ինչպես նաև ջերմաստիճանի հավասարեցման արագությունը տեղի է ունենում ջերմաչափի ջերմային հզորությունը իջեցնելու հետ մեկտեղ, համեմատած մարմնի ուսումնասիրության հետ, սովորաբար նվազեցնելով ջերմաչափի չափերը: Ջերմաչափի ջերմային հզորության նվազումը նույնպես նվազեցնում է չափման արդյունքները, քանի որ ուսումնասիրվող մարմնի ջերմության փոքր մասը տեղափոխվում է կամ փոխանցվում է ջերմաչափին: Իդեալական ջերմաչափը զրոյական ջերմային հզորություն ունի :

Ջերմաստիճանի չափման միջոցներ՝ Ցելսիուսի կամ Ֆարենհայտի սանդղակներ:

Գործնականում ջերմաստիճանի չափուման համար կիրառվում է նաև

• հեղուկ եւ մեխանիկական ջերմաչափեր,
• ջերմատուն,
• դիմադրության ջերմաչափ,
• գազային ջերմաչափ,
• Պիրոմետր:

Առավել ճշգրիտ գործնական ջերմաչափը պլատինային դիմադրության ջերմաչափն է  : Լազերային ճառագայթման չափման հիման վրա մշակվում են ջերմաստիճանի չափման նորագույն մեթոդներ ։

Ջերմաստիճանի չափման սանդղակը և միավորները

Հիմնական հոդված՝ Ջերմաստիճանի չափման միավորները

Այն փաստը, որ ջերմաստիճանը մոլեկուլների կինետիկ էներգիան է, պարզ է, որ դա բնական է չափել էներգետիկ միավորներում (այսինքն, SI համակարգում, տես նաեւ eV): Այնուամենայնիվ, ջերմաստիճանի չափումը սկսվել է դեռևս մոլեկուլային-կինետիկ տեսության ստեղծումից առաջ, այնպես որ գործնական սանդղակներով ջերմաստիճանը չափում են  պայմանական միավորների համակարգում՝  աստիճաններով:

Բացարձակ ջերմաստիճան: Կելվինի ջերմաստիճանը

Հիմնական հոդված՝ Կելվին

Բացարձակ ջերմաստիճանի հասկացությունը ներկայացրեց ՈՒ. Թոմսոնը (Կելվին), ըստ որի բացարձակ ջերմաստիճանի սանդղակը կոչվում է Կելվինի սանդղակ կամ մթնոլորտային ջերմաստիճան: Բացարձակ ջերմաստիճանի միավորը Կելվինն (K) է:

Բացարձակ ջերմաստիճանը է կոչվում, քանի որ  ջերմաստիճանի ցածր սահմանային հորիզոնականը՝ բացարձակ զրոն է, այսինքն, ամենացածր հնարավոր ջերմաստիճանը, ըստ որի սկզբունքորեն հնարավոր չէ ջերմային էներգիա հանել նյութից:

Բացարձակ զրոն ներկայացված է այսպես՝ 0 K, որը հավասար է -273.15 °C և -459.67 °F:

Կալվինի ջերմաստիճանը սանդղակ է, որը սկսվում է բացարձակ զրոյից:

Կելվինի սանդղակը կարևոր նշանակություն ունի գործնականում կիրառվող միջազգային սանդղակներում, ելակետային կետերի հիման վրա մաքուր նյութերի փուլային անցումը առաջնային որոշվում է ջերմաչափերի միջոցով: Առաջին միջազգային ջերմաստիճանային սանդղակը ընդունվել է 1927 թ.՝ ՄՏՍ-27: 1927 թ.-ից սկսած սանդղալը մի քանի անգամ վերանայվել է (ՄՏՍ-48, ՄՊՏՍ-68, ՄՏՍ-90).  հիմնական ջերմաստիճանն ու ինտերպոլյացիոն մեթոդները փոխվել են, սակայն սկզբունքը մնաց նույնը: Ներկայումս գործում է ՄՏՍ-90 սանդղակը: Հիմնական փաստաթուղթը (սանդղակների մասին կանոնակարգ) սահմանում է Կելվինի սահմանումը, ֆազային անցումների ջերմաստիճանի արժեքները (ուղիները) և ինտերպոլացիայի մեթոդները:

Ամենօրյա կյանքում օգտագործվող ջերմաստիճանի սանդղակները Ցելսիուսը և Ֆարենհայտ (օգտագործում են հիմնականում ԱՄՆ-ում), բացարձակ են և անհարմար են փորձերի անցկացման համար, երբ ջերմաստիճանը ջրի սառեցման աստիճանից ցածր է, ապա ջերմաստիճանը  արտահայտվում է բացասական թիվով: Նման դեպքերում, ներկայացվել են բացարձակ ջերմաստիճանի սանդղակներ:

Նրանցից մեկը կոչվում է Ռանկինի սանդղակ, իսկ մյուսը կոչվում է բացարձակ թերմոդինամիկ սանդղակ (Կելվինի սանդղակ), այս սանդղակներով ջերմաստիճանները համապատասխանաբար չափվում են Ռանկինի (° Ra) և Կելվինի (K) աստիճաններով: Երկու սանդղակները սկսվում են բացարձակ զրոյից:

Նրանք տարբերվում են, նրանով որ Կելվինի սանդղակով մեկ բաժնի գինը հավասար է Ցելսիուսի սանդղակի բաժանման գնին, իսկ Ռանկինի սանդղակի բաժանման գինը համարժեք է Ֆարենհայտի սանդղակով ջերմաչափերի բաժանման գնին: Ստանդարտ մթնոլորտային ճնշման տակ ջրի սառեցման ջերմաստիճանը համապատասխանում է 273.15 K, 0 ° C, 32 ° F:

Կելվինի սանդղակի մասշտաբըը կապված է ջրի եռակի  մակարդակի հետ (273.16 К), իսկ Բոլցմանի մշտական կախվածությունը դրա վրա է: Դա առաջացնում է խնդիրներ բարձր ջերմաստիճանի չափման ճշգրտությունը ապահովելու համա ր:Այժմ Միջազգային բյուրոյի կշիռներով եւ միջոցառումներից հաշվի ենք առնում անցումը դեպի  կելվինի նոր սահմանմանին, որը թվային արժեք է՝ Բոլցմանի հաստատունը,որի չափման համար պարտադիր չէ   եռակի մակարդակի ջերմաստիճանի որոշումը:

ՑԵլսիուսի սանդղակ

Հիմնական հոդված՝ ՑԵլսիուսի սանդղակ

Ճարտարագիտության, բժշկության, օդերեւութաբանության մեջ և տանը Ցելսիուսի սանդղակը օգտագործվում է, որպես ջերմաստիճանի չափման միավոր: Ներկայումս SI համակարգում Ցելսիուսի թերմոդինամիկ սանդղակը որոշվում է Կելվինի սանդղակով `t (° C) = T (K) - 273.15 (ճշգրտորեն), այսինքն, Ցելսիուսի սանդղակով մեկ բաժանման գինը հավասար է Կելվինի բաժանման սանդղակին: Ցելսիուսի սանդղակով ջրի եռակի ջերմաստիճանը կազմում է մոտավորապես 0.008 ° C, , ուստի ջրի սառեցման աստիճանը 1 ատմ. ճնշման տակ շատ մոտ է 0 ° C- ին: Ջրի եռման աստիճանը սկզբնապես ընտրվել է Ցելսիուսի կողմից, որպես 100°С: Ըստ ժամանակակից գնահատականների, ջերմաստիճանի նորմալ մթնոլորտային ճնշման տակ ջրի եռման կետը Ցելսիուսի թերմոդինամիկական սանդղակում կազմում է մոտ 99.975 ° C: Ցելսիուսի  սանդղակը շատ հարմար է գործնական տեսանկյունից, քանի որ մեր մոլորակում շատ տարածված է ջուրը, և մեր կյանքը հիմնված է դրա վրա: Ցելսիուսի զրոյականը օդերևութաբանական հատուկ կետ է, քանի որ այն կապված է մթնոլորտային ջրի սառեցման հետ: Սանդղակը 1742-ին առաջարկել է Անդերս Ցելսիուսը:

Ֆարենհայտի սանդղակ

Հիմնական հոդված՝ Ֆարենհայտի սանդղակ

Անգլիայում և, մասնավորապես, ԱՄՆ-ում, օգտագործվում է Ֆարենհեյթի սանդղակը: Զրոյական աստիճան ցելսիուսը համապատասղանում է 32 աստիճան Ֆարենհեյթի, իսկ 100 աստիճանի ցելյոսը `212 աստիճան Ֆարենհայտի:

Ներկայումս Ֆարենհեյթի սանդղակի սահմանումն ընդունվում է այսպես. Այն ջերմաստիճանի մասշտաբ է, որի 1 աստիճանը (1 ° F) հավասար է 1/180 ջերմաստիճանի միջև եղած տարբերության և մթնոլորտի միջև ջերմաստիճանի մթնոլորտային ճնշման , և սառույցի հալման կետն ունի +32 ° F ջերմաստիճան: Ֆարենհայտիի սանդղակի վրա ջերմաստիճանը պայմանավորված է Ցելսիուսի ջերմաստիճանային սանդղակով (t ° C) t ° C = 5/9 (t ° F-32), t ° F = 9/5 t ° C + 32. Սանդղակը առաջարկավել է 1724 թ. Գ. Ֆարենհայտի կողմից:

Ռեոմյուրի սանդղակ

Հիմնական հոդված՝ Ռեոմյուրի սանդղակ

Այն առաջարկվել է 1730 թ. Ռ. Ա. Ռեոմյուրի կողմից, որը նկարագրել է իր հորինած ալկոհոլային ջերմաչափը:

Ռեոմյուրի միավորը (° Ré) աստիճանն է, 1 ° Ré հավասար է 1/80 ջերմաստիճանի, սառույցի հալման ջերմաստիճանը (0 °Ré), իսկ ջրի եռման ջերմաստիճանը (80 °Ré) է:

1 °Ré = 1,25 °C:

Ներկայումս սանդղակը չի օգտագործվում, այն երկար կիրառվել է Ֆրանսիայում` հեղինակի հայրենիքում:

Ջերմային շարժման էներգիան բացարձակ զրոյի պայմաններում

Երբ մատերիան սառչում է, ջերմային էներգիայի և դրանց հետ կապված ազդեցությունների բազմաթիվ ձևերը միաժամանակ նվազում են:Նյութը անցնում է ավելի քիչ կարգավորված վիճակից դեպի ավելի կարգավորվածը:

«... բացարձակ զրոյի ժամանակակից հայեցակարգը բացարձակ հանգստության գաղափար չէ, ընդհակառակը, բացարձակ զրոյի դեպքում կարող է շարժում լինել, և դա ամբողջական կարգավիճակ է ...

Պ. Լ. Կապիցա»

Գազը վերածվում է հեղուկի և այնուհետեւ բյուրեղացվում է ամուր մարմնի ( բացարձակ զրո մթնոլորտային ճնշման դեպքում հելիումը մնում է հեղուկ վիճակում ): Ատոմների և մոլեկուլների շարժումը դանդաղում է, դրանց կինետիկ էներգիան նվազում է: Մետաղների մեծամասնության դիմադրությունը ընկնում է էլեկտրոնների ցրման նվազման շնորհիվ, բյուրեղյա ցանցի ատոմների ավելի փոքր ամպլիտուդի թրթռանքով: Այսպիսով, նույնիսկ բացարձակ զրոյի դեպքում, էլեկտրոնները շարժվում են ատոմների որոշակի արագությամբ, որն ըստ Ֆերմի հավասար է 10⁶ մ / վ:

Ջերմաստիճանը, որում նյութի մասնիկները ունեն նվազագույն քանակի արագություն, որը պահպանվում է միայն քվանտային մեխանիկական շարժման միջոցով անվանում են բացարձակ զրոյական ջերմաստիճանը (T = 0K):

Ջերմաստիճանները բացարձակ զրոյականի հասնել չեն կարող: 2003 թ-ին ՄՏԻ- ի հետազոտողները ստացել են ամենացարծր ջերմաստիճանը (450 ± 80) ·10⁻¹² К, որն ստացել Բոզե-Այնշտայնը նատրիումի ատոմների կոնդենսատորից: Այս դեպքում ջերմային ճառագայթման ալիքի երկարությոոնը կազմում է 6400 կիլոմետր, որմ մոտավորապես հավասար է Երկրի շառավղին:

Ջերմաստիճանը եւ ճառագայթումը

Մարմնի կողմից արտանետվող էներգիան համաչափ է իր ջերմաստիճանի չորրորդ փուլին: Այսպիսով, 300 կիլոմետր քառակուսի մակերեսի դեպքում հասնում է մինչև  450 վտ: Այսպես բացատրվում է, օրինակ,  ձմռանը երկրի մակերևույթի  օդի ջերմաստիճանից ցածր լինելը:  Բացարձակապես սև մարմնի ճառագայթային էներգիան նկարագրվում է Ստեֆան-Բոլցման օրենքով:

Անցումներ տարբեր սանդղակներից

Հիմնական սանդղակների միջև ջերմաստիճանի վերահաշվարկը

Սանդղակ	Նշան	Ցելսիուսից (°C)	Ցելսիուս
Ֆարենհայտ	(°F)	[°F] = [°C] × 9⁄5 + 32	[°C] = ([°F] − 32) × 5⁄9
Կելվին	(K)	[K] = [°C] + 273,15	[°C] = [K] − 273,15
Ռանկին (Rankin)	(°R)	[°R] = ([°C] + 273,15) × 9⁄5	[°C] = ([°R] − 491,67) × 5⁄9
Դելիսլե (Delisle)	(°Д или °De)	[°De] = (100 − [°C]) × 3⁄2	[°C] = 100 − [°De] × 2⁄3
Նյուտոն (Newton)	(°N)	[°N] = [°C] × 33⁄100	[°C] = [°N] × 100⁄33
Ռեոմոյուր (Réaumur)	(°Re, °Ré, °R)	[°Ré] = [°C] × 4⁄5	[°C] = [°Ré] × 5⁄4
Ռյոմեր (Rømer)	(°Rø)	[°Rø] = [°C] × 21⁄40 + 7,5	[°C] = ([°Rø] − 7,5) × 40⁄21

Ջերմաստիճանի կշիռների համեմատություն

Ջերմաստիճանի սանդղակների համեմատություն

Նկարագրություն	Կելվին	Ցելսիում	Ֆարենհայտ	Ռանկին	Դելիսլե	Նյուտոն	Ռեոմյուր	Ռյոմեր
Բացարձակ զրո	0	−273,15	−459,67	0	559,725	−90,14	−218,52	−135,90
Ֆարենհայտի խառնուրդի հալվածքի ջերմաստիճանը (հավասար քանակությամբ աղ և սառույց)	255,37	−17,78	0	459,67	176,67	−5,87	−14,22	−1,83
Ջրի սառեցման ջերմաստիճան (նորմալ պայմաններ)	273,15	0	32	491,67	150	0	0	7,5
Մարդու մարմնի միջին ջերմաստիճան¹	309,75	36,6	98,2	557,9	94,5	12,21	29,6	26,925
Ջրի եռման ջերմաստիճան (նորմալ պայմաններ)	373,15	100	212	671,67	0	33	80	60
Տիտանի հալեցում	1941	1668	3034	3494	−2352	550	1334	883
Արև²	5800	5526	9980	10440	−8140	1823	4421	2909

¹ Մարդու մարմնի բնականոն միջին ջերմաստիճանը +36.6 ° C ± 0.7 ° C է կամ +98.2 ° F ± 1.3 ° F. +98.6 ° F- ի սովորական արժեքը ճշգրիտ փոխակերպումն է 19-րդ դարում Գերմանիայում +37 ° C արժեքով Ֆարենհեյթի սանդղակին: Այնուամենայնիվ, այդ արժեքը չի ընկնում մարդու բնականոն միջին ջերմաստիճանի սահմաններում, քանի որ մարմնի տարբեր մասերի ջերմաստիճանը տարբեր է:

² Այս աղյուսակում որոշ արժեքներ կլորացվում են: Օրինակ, արեւի մակերեւութային ջերմաստիճանը հավասար է 5800 աստիճանով Կելվիին: Այնուամենայնիվ, մնացած ջերմաստիճանների համար, արդեն իսկ տրվել է 5800 աստիճանով Կելվինի ճշգրիտ արդյունքը:

Ֆազային անցումների բնութագիրը

Նկարագրելու համար տարբեր նյութերի փուլային անցումների բնութագիրը, օգտագործվում են հետևյալ ջերմաստիճանի արժեքները.

• Հալման ջերմաստիճան
• Եռման ջերմաստիճան
• Այրման ջերմաստիճան
• Խտացման ջերմաստիճան
• Սինթեզի ջերմաստջիճան
• Հողի ջերմաստիճան
• Հոմոլոգիական ջերմաստիճան
• Եռակի կետ
• Դեբայի ջերմաստիճան (բնութագրական ջերմաստիճան)
• Կյուրիի ջերմաստիճան
• Նելի ջերմաստիճան

Ընկալման հոգեբանություն

Քանի որ բազմաթիվ փորձերի արդյունքները ցույց են տալիս, որ ցրտի կամ ջերմության զգացումը կախված է ոչ միայն շրջակա միջավայրի ջերմաստիճանից, այլև տրամադրությունից:

Այսպիսով, եթե ուսումնասիրվողը զգում է իրեն միայնակ, օրինակ, գտնվում է մարդկանց հետ մի սենյակում, որը չի կիսում իր տեսակետները կամ արժեքները, կամ պարզապես հեռու է այլ մարդկանցից, ապա սենյակը դառնում է ավելի սառը, և հակառակը:

  Հետաքրքիր փաստեր

• Ամենաբարձր ջերմաստիչանը ստեղծվել է մարդու կողմից 2010 թ.-ին՝ մոտավորապես 10 տրլն К, (որը համապատասխանում է իր կյանքի առաջին վարկյանների տիեզերական ջերմաստիճանին) կապարի իոնների բախման ժամանակ, արագացված մոտ լույսի արագությամբ: Փորձը կատարվել է Մեծ Ադրոն Կոլլերի կողմից :

• Տեսականորեն հնարավոր ամենաբարձր ջերմաստիճանը դա Պլանկի ջերմաստիճանն է: Ավելի բարձր ջերմաստիճան չի կարող գոյություն ունենալ ժամանակակից ֆիզիկական հասկացությունների համաձայն, քանի որ լրացուցիչ էներգիա ավելացնելու համար նման  ջերմաստիճանը չի բարձրացնում մասնիկների արագությունը, այլ միայն բախումներ է առաջացնում նոր մասնիկների հետ, իսկ համակարգում մասնիկների թիվը և զանգվածը աճում է: Դա մոտավորապես հավասար է 1,41679(11)·10³² K (մոտ 142 նոնիլիոն K):
• Արևի մակերևույթը մոտավորապես 6000 K ջերմաստիճան ունի, իսկ արևի միջուկը, մոտ 15.000.000 K.:
• Մարդու կողմից ամենացածր ջերմաստիճանը ստացվել է 1995 թվականին, ԱՄՆ-ում Էրիկ Կոռնելի և Կարլ Վիմանի կողմից, ռուբիդիումի ատոմների սառեցմամբ  : Այն բացարձակ զրոյից բարձր էր, քան կալվինի 1/170 միլիարդերորդը (5,9·10⁻¹² K):
• Երկրի մակերևույթում գրանցված ցածր ջերմաստիճանը` -89.2 ° C, 1983 թ. Հուլիսի 21-ին գրանցվել է Խորհրդային Ներքին գիտական « Վոստոկ » կայանում (Անտարկտիդա) (ծովի մակերեւույթից 3488 մ բարձրության վրա):
• 9 դեկտեմբերի, 2013 թ. Ամերիկյան երկրաֆիզիկական միության կոնֆերանսում մի խումբ ամերիկացի հետազոտողների հաղորդմամբ, 2010 թ. Օգոստոսի 10-ին, Անտարկտիդայի կետերից մեկում օդի ջերմաստիճանը իջավ մինչեւ -135.8 ° F (-93.2 ° C): Այս տեղեկատվությունը հայտնաբերվել է ՆԱՍԱ-ի արբանյակային տվյալների վերլուծության արդյունքում : Ըստ բանախոսի, Տ. Սկամբոսի (անգլերեն Ted Scambos) զեկույցի ձեռք բերված արժեքը չի գրանցվի որպես ռեկորդ, որը որոշվում է արբանյակային չափումներով, այլ ոչ թե ջերմաչափի օգտագործմամբ :
• Երկրի մակերեւույթի +56.7 ˚C ռեկորդային բարձր օդի ջերմաստիճանը գրանցվել է 1913 թ. հուլիսի 10-ին, Կանադայի Death Valley- ում (Կալիֆորնիա, ԱՄՆ) Գրենլանդի ռանչոում:
• Բարձրագույն բույսերի սերմերը պահպանվում են մինչեւ -269 ° C ցրտից հետո:

Տես նաև

• Բացասական բացարձակ ջերմաստիճան
• Գույնի ջերմաստիճան
• Պայծառության ջերմաստիճան
• Անտենային ջերմաստիճան
• Ջերմային պոմպ

• Վիրտուալ ջերմություն

• Օդի ջերմաստիճանը

• Մարմնի ջերմաստիճանը

• Ջերմաչափ