Հիպերխորանարդ

Հիպերխորանարդ, խորանարդի ընդհանրացված դեպքը կամայական թվով չափումների դեպքում։
Ν չափումներով հիպերխորանարդ է կոչվում Ν-աչափ էվկլիդյան հարթության այն կետերի բազմությունը, որոնք բավարարում են անհավասարությանը, որտեղ a-ն հիպերխորանարդի կողի երկարությույնն է։
Հիպերխորանարդը կարելի է որոշել նաև որպես Ν հավասար հատվածների դեկարտյան արտադրյալ։
Նաև, կարելի է ասել, որ Ν-խորանարդը մարմին է, որի յուրաքանչյուր գագաթ կողերով միացված է մյուս բոլոր գագաթներին; Ν-ը իր հերթին, որոշում է այդ մարմնի չափումները։ Կամ, կարող ենք ասել, որ Ν-աչափ խորանարդը առաջանում է Ν զույգ զուգահեռ (Ν-1)-հարթություններից, այնսինք, ունի 2Ν հիպերնիստ, որոնցից յուրաքանչյուրը (Ν-1)-խորանարդ է։
Ընդհանուր դեպքում Ν-աչափ խորանարդի K-աչափ նիստերի քանակը հավասար է ։
Հիպերխորանարդի բնութագրիչները[խմբագրել | խմբագրել կոդը]
| Բնութագրիչ | Արժեք |
|---|---|
| Կողի երկարություն | a |
| Չափ | N |
| Հիպերծավալ | |
| Մակերևույթի հիպերմակերես | |
| Անկյունագծի երկարություն |
Կառուցումը[խմբագրել | խմբագրել կոդը]
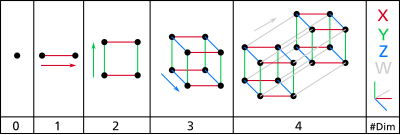
Տարբեր հիպերխորանարդներ[խմբագրել | խմբագրել կոդը]
 Հատված |
 Քառակուսի |
 Խորանարդ |
 4-խորանարդ (tesseract) |
 5-խորանարդ (penteract) |
 6-խորանարդ (hexeract) |
 7-խորանարդ (hepteract) |
 8-խորանարդ (octeract) |
 9-խորանարդ (enneract) |
 10-խորանարդ (dekeract) |
 11-խորանարդ (hendekeract) |
 12-խորանարդ (dodekeract) |

Հիպերխորանարդները գեղարվեստական գրականությունում[խմբագրել | խմբագրել կոդը]
- Ռոբերտ Հայբլայն։ Տուն, որը կառուցել էր Թիլը։
- Ռոբերտ Շեկլի։ Միս Մկնիկն ու չորրորդ չափումը։
- Էդվին Էբոտ։ Ֆլատլանդիա։
- Ուոլտեր Տեվիս։ Նոր չափումներ։
Հրապարակումներ[խմբագրել | խմբագրել կոդը]
- Bowen, J. P. (April 1982). «Hypercubes». Practical Computing. 5 (4): 97–99. Արխիվացված է օրիգինալից 2008 թ․ հունիսի 30-ին. Վերցված է 2014 թ․ դեկտեմբերի 3-ին.
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). Dover. էջեր 123. ISBN 0-486-61480-8. p. 296, Table I (iii)։ Regular Polytopes, three regular polytopes in n dimensions (n ≥ 5)
- Hill, Frederick J.; Gerald R. Peterson (1974). Introduction to Switching Theory and Logical Design: Second Edition. NY: John Wiley & Sons. ISBN 0-471-39882-9.
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- www.4d-screen.de (Rotation of 4D – 7D-Cube)
- Rotating a Hypercube by Enrique Zeleny, Wolfram Demonstrations Project.
- Stereoscopic Animated Hypercube
- Rudy Rucker and Farideh Dormishian's Hypercube Downloads Արխիվացված 2013-03-26 Wayback Machine
- Հատվածից օկտերակտի (և ստերեոպարի) առաջացման անիմացիան





