Կոտանգենսների թեորեմ
Կոտանգենսների թեորեմը, եռանկյունաչափական թեորեմ է, որը կապ է հաստատում եռանկյանը ներգծված շրջանագծի շառավղի և եռանկյան կողմերի երկարությունների միջև։
Բանաձև[խմբագրել | խմբագրել կոդը]


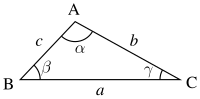
Դիցուք
- -ն եռանկյան երեք կողմերի երկարություններն են,
- -ը՝ համապատասխանաբար կողմերի դիմացի անկյունները,
- -ը՝ եռանկյանը ներգծված շրջանագծի շառավիղ
- -ը՝ եռանկյան կիսապարագիծը։
Այդ դեպքում տեղի ունեն հետևյալ բանաձևերը[1]՝
- ,
- ,
- ,
կամ դրանց համարժեք՝
- :
Թեորեմը կարելի է ձևակերպել հետևյալ կերպ. կիսանկյան կոտանգենսը հավասար է կիսապարագծի և տրված անկյան դիմացի կողմի տարբերության հարաբերությանը ներգծված շրջանագծի շառավղին։
Հետևություն[խմբագրել | խմբագրել կոդը]
Կոտանգենսներից թեորեմից ներգծված շրջանագծի շառավղի համար ստացվում է
- ։
Մյուս կողմից, քանի որ եռանկյան մակերեսը՝ , ապա կարելի է ստանալ Հերոնի բանաձևը՝
Տես նաև[խմբագրել | խմբագրել կոդը]
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.











