Լարերի տեսություն
Լարերի տեսություն, ուղղություն տեսական ֆիզիկայում, որն ուսումնասիրում է ոչ թե կետային մասնիկների[1], այլ միաչափ օբյեկտների՝ այսպես կոչված քվանտային լարերի[2] փոխազդեցության դինամիկան։ Լարերի տեսությունը համադրում է քվանտային մեխանիկայի և հարաբերականության տեսության գաղափարները, այդ պատճառով նրա հիման վրա, հավանաբար, կկառուցվի քվանտային գրավիտացիայի տեսությունը[3][4]։ Լարերի տեսությունը հիմնվում է այն հիպոթեզի վրա[5], որ բոլոր տարրական մասնիկները և նրանց հիմնարար փոխազդեցությունները առաջանում են գերմիկրոսկոպիկ քվանտային լարերի տատանումների և փոխազդեցությունների արդյունքում՝ Պլանկի երկարության կարգի հեռավորությունների վրա՝ մոտ 10−35 մ[2]։ Այս մոտեցումը, մի կողմից, թույլ է տալիս խուսափել դաշտի քվանտային տեսության այնպիսի դժվարություններից, ինչպիսիք են վերանորմավորումը[6], իսկ մյուս կողմից հանգում է նյութի և տարածաժամանակի կառուցվածքի ավելի խոր եզրակացության[6]։ Լարերի տեսությունը առաջացել է 1970-ական թվականներին Գաբրիելե Վենեցիանոյի մի բանաձևի իմաստավորման արդյունքում[7], որը կապված է հադրոնների կառուցվածքի լարային մոդելների հետ։ 1980-ականների և 1990-ականների կեսերը նշանավորվեցին լարերի տեսության բուռն զարգացումով։ Սպասվում էր, որ մոտ ապագայում դրա հիման վրա կձևավորվի այսպես կոչված «միասնական տեսությունը» կամ «ամեն ինչի տեսությունը»[4], որի անհաջող որոնումներով էր զբաղված Այնշտայնը տասնյակ տարիներ[8]։ Սակայն չնայած տեսության մաթեմատիկական խստությանը և ամբողջականությանը, դեռևս լարերի տեսության փորձնական հաստատումներ չեն գտնվել[2]։ Առաջանալով հադրոնային ֆիզիկայի նկարագրման համար, սակայն նպատակահարմար չլինելով դրա համար, այս տեսությունը բոլոր տեսությունների նկարագրման յուրահատուկ փորձարարական վակուում է։
Հիմնական խնդիրներից մեկը, որը առաջանում է լարերի տեսություններում 26 կամ 10 չափականությունից[9] մինչև ցածր էներգիաների 4 չափականությամբ ֆիզիկա կրճատվելու ժամանակ լրացուցիչ չափականությունների կոմպակտավորման բազմաթիվ տարբերակներն են Կալաբի-Յաուի բազմաձևությունների և օրբիձևությունների վրա, որոնք, հավանաբար, Կալաբի-Յաուի տարածության մասնավոր սահմանային դեպքեր են[10]։ Հնարավոր լուծումների մեծ թիվը 1970-ականների վերջին և 1980-ականների սկզբին ստեղծեց «լանդշաֆտի խնդիր» անվանումով խնդիրը[11], ինչի հետ կապված որոշ գիտնականներ կասկածում են, որ արդյոք լարերի տեսությունը կարող է գիտական լինել[12]։
Չնայած այս դժվարություններին, լարերի տեսության մշակումը խթանեց մաթեմատիկական ֆորմալիզմների զարգացմանը, հիմնականում՝ հանրահաշվական և դիֆերենցիալ երկրաչափություններում, տոպոլոգիայում, ինչպես նաև թույլ տվեց ավելի խոր հասկանալ նախորդ՝ քվանտային գրավիտացիայի տեսությունը[2]։ Լարերի տեսությունը շարունակում է զարգանալ, և ակնկալվում է[2], որ տեսության թերի տարրերը և դրանց համապատասխանող երևույթները կբացահայտվեն մոտ ապագայում, այդ թվում Մեծ հադրոնային բախիչի փորձերի միջոցով[13]։
Հիմնական դրույթներ[խմբագրել | խմբագրել կոդը]
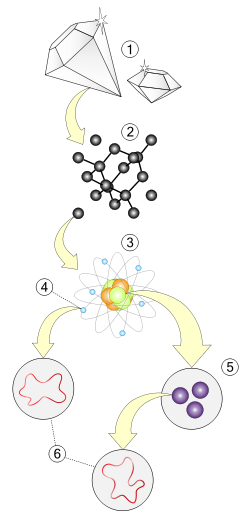
1. Մակրոսկոպիկ մակարդակ՝ նյութ
2. Մոլեկուլային մակարդակ
3. Ատոմային մակարդակ՝ պրոտոններ, նեյտրոններ, էլեկտրոններ
4. Ներատոմային մակարդակ՝ էլեկտրոն
5. Ներատոմային մակարդակ՝ քվարկներ
6. Լարային մակարդակ
Եթե գոյություն ունենար լարերը ցածր էներգիաների ֆիզիկայում արտապատկերելու մեխանիզմ, ապա լարերի տեությունը բոլոր հիմնարար մասնիկները և նրանց փոխազդեցությունները կներկայացներ մեզ ոչ լոկալ միաչափ օբյեկտների գրգռումների սպեկտրի վրա դրված սահմանափակումների տեսքով։ Կոմպակտացված լարերի բնութագրական չափերը խիստ փոքր են՝ 10−33 սմ (Պլանկի երկարության) կարգի, այդ պատճառով նրանք մատչելի չեն փորձում դիտարկելու համար[2]։ Երաժշտական գործիքի լարերի տատանումների նման, քվանտային լարերի սպեկտրային բաղադրիչները հնարավոր են միայն որոշակի հաճախությունների (քվանտային լայնույթների) համար։ Որքան մեծ է հաճախությունը, այնքան մեծ է հաճախության մեջ կուտակված էներգիան[14], և, ըստ E=mc² բանաձևի, այնքան մեծ է մասնիկի զանգվածը, որի դերում դիտարկվող աշխարհում հանդես է գալիս տատանվող լարը։ Լարի համար տատանակի հաճախությանը համանման պարամետրը զանգվածի քառակուսին է[15]։
Ոչ հակասական և ինքնահամաձայնեցված լարերի քվանտային տեսությունները հնարավոր են մ իայն մեծ չափականություններով տարածություններում (չորսից մեծ՝ հաշվի առնելով ժամանակի հետ կապված չափականությունը)։ Սրա հետ կապված լարերի տեսության ֆիզիկայում բաց է տարածաժամանակի չափականության հարցը[16]։ Այն, որ միկրոսկոպիկ (անմիջականորեն դիտարկելի) աշխարհում նկատելի չեն լրացուցիչ տարածական չափումներ, լարերի տեսությունում բացատրվում է երկու հնարավոր մեխանիզմներից մեկով․ այդ չափականությունների կոմպակտավորմամբ, երբ չափականությունները փաթափվում են մինչև Պլանկի երկարության կարգի մասշտաբներում, կամ բազմաչափ տիեզերքի (բազմատիեզերքի) բոլոր մասնիկների լոկալացմամբ քառաչափ համաշխարհային թերթում, որը և բազմատիեզերքի տեսանելի մասն է։ Ենթադրվում է, որ ավելի մեծ չափականությունները կարող են ի հայտ գալ բարձր էներգիաներով տարրական մասնիկների փոխազդեցություններում, սակայն մինչև հիմա փորձարարական վկայություններ չկան։
Լարերի տեսության կառուցման ժամանակ տարբերակում են առաջնային և երկրորդային քվանտացումների մոտեցումները։ Վերջինս կիրառում է լարային դաշտի հասկացությունը՝ ֆունկցիոնալ օղակների տարածությունում, ինչպես դաշտի քվանտային տեսությունը։ Առաջնային քվանտացման ֆորմալիզմում մաթեմատիկական մեթոդներով նկարագրվում է փորձական լարի շարժումը արտաքին լարերի դաշտերում, այդ թվում՝ լարերի տրոհումը և միավորումը։ Առաջնային քվանտացման մոտեցումը լարերի տեսությունը համաշխարհային հարթության վրա կապում է սովորական դաշտի տեսության հետ[4]։
Լարերի ավելի իրատեսական տեսությունները որպես պարտադիր տարր ներառում են սուպերսիմետրիան, այդ պատճառով այդպիսի տեսությունները կոչվում են գերլարային[17]։ Ցածր էներգիաների դեպքում դիտվող մասնիկների համախումբը և նրանց փոխազեցությունները գործնականում վերարտադրվում են տարրական մասնիկների ֆիզիկայի ստանդարտ մոդելով, ընդ որում ստանդարտ մոդելի շատ հատկություններ փայլուն բացատրվում են գերլարերի տեսությունների շրջանակներում։ Այնուհանդերձ մինչ այժմ չկան այնպիսի սկզբունքներ, որոնց օգնությամբ հնարավոր կլիներ բացատրել լարային տեսությունների այս կամ այն սահմանափակումները, որպեսզի ստանայինք ստանդարտ մոդելի նման մի բան[18]։
1980-ականների կեսերին Մայքլ Գրինը և Ջոն Շվարցը եկան եզրակացության, որ սուպերսիմետրիան, որը լարերի տեսության կենտրոնական օղակն է, կարելի է ներառել ոչ թե մեկ, այլ երկու եղանակներով։ Առաջինը լարի համաշխարհային մակերևույթի սուպերսիմետրիան է[4], երկրորդը՝ տարածաժամանակային սուպերսիմետրիան[19]։ Սուպերսիմետրիան ներառելու այս եղանակները իրենց հիմքում դաշտի կոնֆորմ տեսության մեթոդները կապում են դաշտի քվանտային տեսության ստանդարտ մեթոդներին[20][21]։ Սուպերսիմետրիան ներառելու այս եղանակների իրականացման տեխնիկական առանձնահատկությունները պայմանավորեցին հինգ տարբեր լարերի տեսությունների առաջացմանը՝ I տիպի, IIA և IIB տիպի և երկու հետերոտիկ լարերի տեսություններ[22]։ Սրա արդյունքում առաջացած հետաքրքրության բռնկումը լարերի տեսության հանդեպ կոչվեց «առաջին գերլարային հեղափոխություն»։ Այս բոլոր մեթոդները ձևակերպվում են 10-չափանի տարածաժամանակում, սակայն տարբերվում են լարային սպեկտրներով և սիմետրիայի տրամաչափային խմբերով։ 1970-ականներին սկզբնավորված և 1980-ականներին զարգացած 11-չափանի սուպերգրավիտացիայի կառուցվածքը[23], ինչպես նաև փուլային փոփոխականների անսովոր տոպոլոգիական երկվությունները լարերի տեսությունում 1990-ականների կեսերին հանգեցրին «երկրորդ գերլարային հեղափոխությանը»։ Պարզվեց, որ այս բոլոր տեսությունները իրականում սերտորեն կապված են միմյանց հետ որոշակի երկվությունների շնորհիվ[24]։ Ենթադրվեց, որ բոլոր հինգ տեսությունները մեկ հիմնարար տեսության տարբեր սահմանային դեպքեր են, որը ստացավ М-տեսություն անվանումը։ Ներկայումս որոնումներ են արվում այս տեսությունը ձևակերպելու մաթեմատիկական լեզու ստեղծելու համար[18]։
Պատմություն[խմբագրել | խմբագրել կոդը]
Լարերը հադրոնային ֆիզիկայում[խմբագրել | խմբագրել կոդը]

Որպես հիմնարար օբյեկտներ, լարերը սկզբնապես ներմուծվել են տարրական մասնիկների ֆիզիկայում հադրոնների, մասնավորապես պիոնների կառուցման առանձնահատկությունները բացատրելու համար։
1960-ական թվականներին կախվածություն նկատվեց հադրոնի սպինի և զանգվածի միջև (Չու-Ֆրաուչիի գրաֆիկ)[25]։ Այս դիտարկման արդյուքնում ստեղծվեց Ռեջեի տեսությունը, որտեղ տարբեր հադրոններ դիտարկվում են որպես ոչ թե տարրական մասնիկներ, այլ՝ մեկ տարածականացված օբյեկտի՝ ռեջեոնի տարբեր դրսևորումներ։ Վերջին տարիներին Գաբրիելե Վենեցիանոյի, Յոիտիրո Նամբուի, Հոլգեր Բեխ Նիլսոնի և Լեոնարդ Սասկինդի ջանքերով բանաձև արտածվեց ռեջեոնների ցրման համար և տրվեց դրա ընթացքում տեղի ունեցող երևույթների լարային մեկնաբանությունը։
1968 թվականին Գաբրիելե Վենեցիանոն և Մախիկո Սուձուկին պի-մեզոնների բախումները վերլուծելու փորձերի ժամանակ նկատեցին, որ բարձրէներգիական պիոնների զույգային ցրման ամպլիտուդը ճշտորեն նկարագրվում է 1730 թվականին Լեոնադ Էյլերի ներմուծած բետա-ֆունկցիաներից մեկով։ Ավելի ուշ պարզ դարձավ, որ զույգային պիոնային ցրման ամպլիտուդը կարող է վերլուծվել անվերջ շարքի, որի սկիզբը համընկնում է Վենեցիանո-Սուձուկիի բանաձևի հետ[26]։
1970 թվականին Յոիտիրո Նամբուն, Տեցո Գոտոն, Հոլգեր Բեխ Նիլսենը և Լեոնարդ Սասկինդը մի գաղափար առաջ քաշեցին, որ բախվող պիոնների միջև փոխազդեցություն է առաջանում այն բանի հետևանքով, որ այս պիոնները միավորված են «անվերջ բարակ տատանվող թելով»։ Ենթադրելով, որ այդ «թելը» ենթարկվում է քվանտային մեխանիկայի օրենքներին, նրանք արտածեցին Վենեցիանո-Սուձուկիի բանաձևի հետ համընկնող բանաձև։ Այսպիսով, ի հայտ եկան մոդելներ, որոնցում տարրական մասնիկները ներկայանում են միաչափ լարերի տեսքով, որոնք տատանվում են որոշակի հաճախություններով[26]։
Քվանտային քրոմոդինամիկայի մշակմանը զուգահեռ գիտական հասարակությունը հետարքրքրությունը կորցրեց հադրոնային ֆիզիկայի լարային տեսության հանդեպ մինչև 1980-ականները[2]։
Լարերի բոզոնային տեսություն[խմբագրել | խմբագրել կոդը]
1974 թվականին պարզ դարձավ, որ Վենեցիանոյի բանաձևի վրա հիմնված լարային տեսությունները գործում են 4-ից մեծ չափականություններով տարածությունում․ Վենեցիանոյի մոդելը և Շապիրո-Վիրասորոյի մոդելը (S-V) 26 չափականությունում, Ռամոն-Նեվյո-Շվարցի մոդելը (R-NS)՝ 10-ում։ Դրանք բոլորը կանխատեսում են տախիոնի գոյությունը[27]։ Տախիոնների արագությունը գերազանցում է վակուումում լույսի արագությանը, այդ պատճառով նրանց գոյությունը հակասում է պատճառականության սկզբունքին, որն, իր հերթին, խախտվում է միկրոաշխարհում։ Այսպիսով, տախիոնի գոյությունը ապացուցող (առաջին հերթին փորձարարական), կամ հերքող փաստարկներ[28]։ Ներկայումս ավելի գերադասելի է համարվում ֆիզիկական տեսություններ կառուցելիս տախիոնները գաղափարը չկիրառելը։ Տախոնների խնդրի լուծումը հիմնված է ըստ տարածաժամանակային գլոբալ սիմետրիայի (Կոորդինատներից կախում չունեցող) Վեսսի և Զումինոյի աշխատանքների վրա (1974 թվական)[29]։ 1977 թվականին Գլիոցին Ջոել Շվերկը և Դեյվիդ Օլիվը (GSO պրոեկցիա) R-N-S մոդելում ներմուծեցին հատուկ պրոեկցիա լարային փոփոխականների համար, ինչը թույլ տվեց վերացնել տախիոնը և ըստ էության սուպերսիմետրիկ լար տվեց[30]։ 1981 թվականին Գրինին և Շվարցին հաջողվեց նկարագրել GSO պրոեկցիան D-չափանի սուպերսիմետրիայի տերմիններով և ավելի ուշ լարերի տեսության մեջ ներմուծել անոմալիաների բացառման սկզբունքը[31]։
1974 թվականին Ջոն Շվարցը և Ժոել Շվերկը, ինչպես նաև նրանցից անկախ Տամիակի Յոնեան, ուսումնասիրելով որոշ լարայիննկատեցին, որ դրանք ճշտությամբ համապատասխանում են հիպոթետիկ մասնիկի՝ գրավիտացիոն դաշտի քվանտի հատկություններին[32]։ Շվարցը և Շվերկը պնդում էին, որ լարերի տեսությունը սկզբում անհաջողություն կրեց այն պատճառով, որ ֆիզիկոսները թերագնահատում էին դրա մասշտաբը[18]։ Այս մոդելի հիման վրա ստեղծվեց բոզոնային լարերի տեսությունը[4]։ Այս տեսությունը ձևակերպվում է գործողության տերմիններով, որի օգնությամբ կարելի է կանխատեսել լարի շարժումը տարածության և ժամանակի մեջ։ Գործողության քվանտացումը հանգում է նրան, որ լարը կարող է թրթռալ տարբեր եղանակներով և ամեն մի եղանակ գեներացնում է տարբեր տգարրական մասնիկ։ Մասնիկի զանգվածը և փոխազդեցության բնութագրերը որոշվում են լարի թրթռման եղանակներով կամ լարից բխող յուրահատուկ «նոտա»յով։ Այս կերպ ստացված գամման կոչվում է լարերի տեսության զանգվածների սպեկտր։
Սկզբում մոդելում ներառված եին ինչպես բաց լարերը, այսինքն՝ երկու ազատ ծայրեր ունեցող լարերը, այնպես էլ փակ լարերը, այսինքն՝ օղակները։ Այս երկու տիպի լարերը տաևբեր վարք ունեն և երկու տարբեր սպեկտր են գեներացնում։ Ժամանակակից ոչ բոլոր լարերի տեսությաններում են կիրառվում երկու տիպի լարերը․ մի քանիսում միայն փակ լարերն են կիրառվում։
Բոզոնային լարերի տեսությունը զուրկ չէ խնդիրներից։ Ամենից առաջ, տեսությունն ունի հիմնարար անկայություն, որը ենթադրում է հենց իր՝ տարածաժամանակի տրոհումը։ Բացի այդ, ինչպես հետևում է անվանումից, մասնիկների սպեկտրը սահմանափակված է միայն բոզոններով։ Չնայած բոզոնները կարևոր դեր ունեն տիեզերքում, տիեզերքը սահմանափկված չէ միայն նրանցով։ Այն նաև կանխատեսում է բացասական զանգվածի քառակուսի ունեցող մասնիկի՝ տախիոնի գոյությունը[15]։ Ֆերմիոնները լարերի տեսությունում ներառելու հետազոտությունները հանգեցին սուպերսիմետրիայի հասկացությանը՝ բոզոնների և ֆերմիոնների փոխազդեցության տեսությունը, որն այժմ ինքնուրույն նշանակություն ունի։ Լարերի ֆերմիոնային թրթռումները ներառող տեսությունները կոչվում են գերլարային տեսություններ[33]։
Գերլարային հեղափոխություններ[խմբագրել | խմբագրել կոդը]

1984-1986 թվականներին ֆիզիկոսները հասկացան, որ լարերի տեսությունը կարող է նկարագրել բոլոր տարրական մասնիկները և նրանց փոխազդեցությունները․ և հարյուրավոր գիտնականներ սկսեցին աշխատել լարերի տեսության վրա՝ որպես ֆիզիկական տեսությունների միավորման ամենահեռանկարային գաղափարի։
Առաջին գերլարային հեղափոխություն դարձավ 1984 թվականին Մայքլ Գրինի և Ջոն Շվարցի բացահայտումը, որ I տիպի լարերի տեսությունում անոմալիաները կրճատվում են։ Այս կրճատման մեխանիզմը կոչվում է Գրին-Շվարցի մեխանիզմ։ 1985 թվականին այլ էական բացահայտումներ արվեցին, օրինակ՝ հետերոտիկ լարերի բացահայտումը[18]։

1990-ականների կեսերին Էդվարդ Ուիթենը, Ջոզեֆ Պոլչինսկին և այլ ֆիզիկոսներ նկատեցին ծանրակշիռ ապացույցներ այն մասին, որ տարբեր գերլարերի տեսություններ11-չափանի М-տեսության զահմանային դեպքեր են։ Այս բացահայտումով նշանավորվեց երկրորդ գերլարային հեղափոխությունը։
Լարերի տեսության վերջին հետազոտությունները (М-տեսությունը) քննարկում է D-բրանները, բազմաչափ օբյեկտները, որոնց գոյությունը բխում է տեսության մեջ տեսության մեջ բաց լարեր ներառելուց[18]։ 1997 թվականին Խուան Մալդասենան կապ նկատեց լարերի տեսության և տրամաչափային տեսության միջև, որը կոչվում է Յանգ-Միլլասի N=4 սուպերսիմետրիկ տեսություն[4]։ ԱՅս փոխկապակցվածությունը, որը կոչվեց AdS/CFT-համապատասխանություն (անգլերեն կրճատ անտի դե Սիտերի տարածություն՝ anti de Sitter space և կոնֆորմ դաշտի տեսություն արտահայտությունից conformal field theory), ներկայումս մեծ ուշադրություն է վայելում և ակտիվ ուսումնասիրվում է[34]։ AdS/CFT-համապատասխանությունը հոլոգրաֆիկ սկզբունքի իրականացում է, որը հեռուն գնացող հետևանքներ ունի սև խոռոչների, լոկալության և ինֆորմացիայի, ինչպես նաև գրավիտացիոն փոխազդեցության համար։
2003 թվականին մշակվեց լարերի տեսության լանդշաֆտը, որը նշանակում է, որ լարերի տեսությունում գոյություն ունեն էքսպոնենցիալ մեծ թվով ոչ համարժեք կեղծ վակուումներ[35][36][37]։
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ А. А. Комар. «Размер» элементарной частицы // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 3.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 Гросс, Дэвид. Грядущие революции в фундаментальной физике. Проект «Элементы», вторые публичные лекции по физике (25.04.2006).
- ↑ Sunil Mukhi (1999) «The Theory of Strings: A Detailed Introduction» (անգլերեն).
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 А. Ю. Морозов Струн теория // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 5.
- ↑ Scherk J., Schwarz J.H. Dual models for non-hadrons(անգլ.) // Nucl.Phys. — 1974. — В. 1. — Т. 81. — P. 118−144. — ISSN 0550-3213.
- ↑ 6,0 6,1 Морозов А. Ю. Теория струн — что это такое? // УФН. — 1992. — Т. 162, № 8. — С. 83—175.
- ↑ Veneziano G., Nuovo Cim., 1968, 57A, 190 (также неопубликованная работа Suzuki M., 1968) (անգլերեն).
- ↑ Б. Паркер. Мечта Эйнштейна. В поисках единой теории строения Вселенной. — М.: Амфора, 2000. — 333 с. — ISBN 5-8301-0198-Х
- ↑ Polchinski, Joseph (1998). String Theory, Cambridge University Press (անգլերեն).
- ↑ Каку, Мичио. Введение в теорию суперструн / пер. с англ. Г.Э. Арутюнова, А.Д. Попова, С.В. Чудова; под ред. И. Я. Арефьевой. — М.: Мир, 1999. — 624 с. — ISBN 5-03-002518-9.
- ↑ Yau S., Witten E. Simposium on Anomalies, Geometry and Topology, 1985, WS, Singhapur, Witten E.and others Nukl.Phys., 1985, B261, 678; 1986, B274, 286 (անգլերեն).
- ↑ Peter Woit (2001 թ․ փետրվարի 16). «Теория струн: оценка». Արխիվացված է օրիգինալից 2004 թ․ նոյեմբերի 14-ին. Վերցված է 2009 թ․ հոկտեմբերի 31-ին. arXiv:physics/0102051 (անգլերեն).
- ↑ Lisa Randall (2002). «Extra Dimensions and Warped Geometries» (PDF). Science. 296 (5572): 1422–1427. doi:10.1126/science.1072567. PMID 12029124. Արխիվացված է օրիգինալից (PDF) 2018 թ․ հոկտեմբերի 7-ին. Վերցված է 2015 թ․ դեկտեմբերի 12-ին.
- ↑ С. В. Егерев Струна // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 5.
- ↑ 15,0 15,1 Бухбиндер И. Л. Теория струн и объединение фундаментальных взаимодействий. // Соросовский образовательный журнал — 2001, № 7. — С. 99.
- ↑ Барбашов, Б. М., Нестеренко, В. В. Суперструны — новый подход к единой теории фундаментальных взаимодействий // Успехи физических наук. Том 150, № 4. — М.: 1986, с. 489—524.
- ↑ «Новая картина струнной теории». Перевод "Официального Сайта Теории Суперструн". Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 22-ին. Վերցված է 2009 թ․ հոկտեմբերի 1-ին.
- ↑ 18,0 18,1 18,2 18,3 18,4 Грин Б. Элегантная Вселенная. Суперструны, скрытые размерности и поиски окончательной теории: Пер. с англ. / Под ред. В. О. Малышенко. — Изд. 3-е. — М.: Едиториал УРСС, 2007. — 288 с. — ISBN 5-484-00784-4
- ↑ Green M.& Schwarz J. Phys. Lett. 1984, 149B, 117 (անգլերեն).
- ↑ Polyakov A.M. Phys. Lett. 1981, 103B, 207, 211 (անգլերեն).
- ↑ Belavin A.A., Polyakov A.M., Zamolodchikov A.B. Nucl. Phys. 1984, B241, 333 (անգլերեն).
- ↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality «Lecture 23 — Can I Have that Extra Dimension in the Window?», 0:04:54, 0:21:00 (անգլերեն).
- ↑ M. J. Duff, James T. Liu and R. Minasian Eleven Dimensional Origin of String/String Duality: A One Loop Test Center for Theoretical Physics, Department of Physics, Texas A&M University (անգլերեն).
- ↑ «Новая картина струнной теории». Перевод "Официального Сайта Теории Суперструн". Արխիվացված օրիգինալից 2011 թ․ օգոստոսի 22-ին. Վերցված է 2009 թ․ հոկտեմբերի 1-ին.
- ↑ G. F. Chew and S. C. Frautschi, Phys. Rev. Letters, 8, 41 (1962); S. C. Frautschi, «Regge Poles and S-Matrix Theory», (W. A. Benjamin, New York, 1968) (անգլերեն).
- ↑ 26,0 26,1 Левин, А. Струнный концерт для Вселенной Արխիվացված 2007-08-10 Wayback Machine // Популярная механика, март 2006.
- ↑ Shapiro J. Phys. Rev., 1971, 33В, 361. Virasoro M. Phys. Rev., 1969, 177, 2309. Ramond P. Phys. Rev., 1971, D3, 2415. Neveu A.& Schwarz J. Nucl. Phys., 1971, B31, 86.Lovelace C. Phys. Rev., 1974, 34B, 500 (անգլերեն).
- ↑ Ю. П. Рыбаков Тахион // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 5.
- ↑ Wess J., Zumino B. Nucl.Phys. 1974, B70, 39 (անգլերեն).
- ↑ Gliozzi F., Sherk J., Ollive D. Nucl.Phys. 1977, B122, 253 (անգլերեն).
- ↑ Green M.& Schwarz J. Nucl.Phys. 1981, B81, 253, Green M.& Schwarz J. Phys. Lett. 1984, 149B, 117 (անգլերեն).
- ↑ В. И. Огиевецкий Гравитон // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 1.
- ↑ Vladimir G. Ivancevic, Tijana T. Ivancevic. Applied Differential Geometry: A Modern Introduction. — Sydney: World Scientific Publishing Company, 2007. — С. 41. — 1348 с. — ISBN 978-981-270-614-0 (անգլերեն)
- ↑ Статистика опубликованных по тематике статей по годам: AdS/CFT correspondence on arxiv.org (անգլ.)
- ↑ S. Kachru, R. Kallosh, A. Linde and S. P. Trivedi, «de Sitter Vacua in String Theory», Phys.Rev. D68:046005, 2003, arXiv:hep-th/0301240 (անգլերեն).
- ↑ M. Douglas, «The statistics of string / M theory vacua», JHEP 0305, 46 (2003). (անգլերեն).
- ↑ S. Ashok and M. Douglas, «Counting flux vacua», JHEP 0401, 060 (2004) (անգլերեն).
