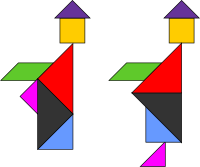
Թանգրամ

Թանգրամ (չին.七巧板, փինյին՝ qī qiǎo bǎn, բառացի՝ «վարպետության յոթ տախտակիկ»), գլուխկոտրուկ՝ կազմված յոթ հարթ ֆիգուրներից, որոնք դասավորվում են որոշակի ձևով մեկ այլ՝ ավելի բարդ պատկեր ստանալու համար (մարդու, կենդանու, կենցաղային առարկայի պատկեր, տառ, թիվ և այլն)։ Ստացվելիք պատկերը սովորաբար սահմանվում է ուրվապատկերի կամ արտաքին ուրվագծի տեսքով։ Գլուխկոտրուկը լուծելու համար պետք է պահպանվի երկու պայման. առաջինը՝ անհրաժեշտ է օգտագործել թանգրամի բոլոր յոթ ֆիգուրները, և երկրորդ՝ ֆիգուրները չպետք է դրվեն իրար վրա։

Պատմություն[խմբագրել | խմբագրել կոդը]

Թանգրամը, հնարավոր է, ծագել է յանցզիտուից (燕几圖). կահույքի տեսակ, որ ի հայտ է եկել Սուն կայսրության շրջանում։ Որպես կահույք՝ յանցզիտուն որոշ փոփոխություններ է կրել Մին դինաստիայի կառավարման տարիներին, իսկ հետագայում վերածվել է խաղի համար նախատեսված փայտե ֆիգուրների հավաքածուի։

Չնայած թանգրամը հաճախ շատ վաղ ժամանակների գյուտ է համարվում, նրա մասին առաջին տպագիր հիշատակությունը հանդիպում է 1813 թվականին հրատարակված չինական գրքում, որն ակնհայտորեն գրվել է Ցզյացին կայսեր օրոք^[1]։

Արևմուտքում թանգրամը ի հայտ է եկել 19-րդ դարի սկզբից ոչ շուտ, երբ այդ գլուխկոտրուկը հայտնվել է Ամերիկայի չինական և ամերիկյան նավերում։ Հնագույն այդպիսի օրինակը, որ 1802 նվիրել են ամերիկացի նավատիրոջ որդուն, պատրաստված է փղոսկրից և պահվում է մետաքսե տուփի մեջ։

«Թանգրամ» բառը 1848 թվականին առաջին անգամ օգտագործել է Հարվարդի համալսարանի ապագա նախագահ Թոմաս Հիլլն իր «Գլուխկոտրուկներ երկրաչափության ուսուցման համար» գրքույկում։

Գրող և մաթեմատիկոս Լուիս Քերոլը համարվում է թանգրամի էնտուզիաստ։ Նրա մոտ պահպանվել է 323 հանձնարարություններով չինական գիրք։

Սուրբ Հեղինեի կղզում աքսորի ժամանակ Նապոլեոնի մոտ եղել են թանգրամի հավաքածու և խնդիրների ու լուծումների գիրք։ Այդ հավաքածուի լուսանկարները ներառված են Ջերրի Սլոկումի «The Tangram Book» գրքում^[2]։

Սեմ Լոյդի «Տանի ութերորդ գիրքը» աշխատությունը, որ տպագրվել է 1903 թվականին, ներկայացնում է թանգրամի մտացածին պատմությունը, համաձայն որի՝ այս գլուխկոտրուկը հորինվել է 4 հազար տարի առաջ Տան անունով աստվածության կողմից։ Գիրքը ներառում է 700 առաջադրանք, որոնցից մի քանիսը լուծված չեն^[3]։

Ֆիգուրներ[խմբագրել | խմբագրել կոդը]

Չափերը ներկայացված են մեծ քառակուսու համեմատությամբ, որի կողմերն ու մակերեսն ընդունվում է հավասար $\scriptstyle {1}$ -ի^[4].

5 ուղղանկյուն եռանկյուն՝
- 2 փոքր (ներքնաձիգը՝ $\scriptstyle {1/2}$ , էջերը՝ $\scriptstyle {{\sqrt {2}}/4}$ ),
- 1 միջին (ներքնաձիգը՝ $\scriptstyle {1/{\sqrt {2}}}$ , էջերը՝ $\scriptstyle {1/2}$ ),
- 2 մեծ (ներքնաձիգը՝ $\scriptstyle {1}$ , էջերը՝ $\scriptstyle {1/{\sqrt {2}}}$ ),
1 քառակուսի ( $\scriptstyle {{\sqrt {2}}/4}$ կողմով),
1 զուգահեռագիծ ( $\scriptstyle {1/2}$ և $\scriptstyle {{\sqrt {2}}/4}$ կողմերով ու $\scriptstyle {45^{\circ }}$ և $\scriptstyle {135^{\circ }}$ անկյուններով)։

Այս յոթ մասերից զուգահեռագիծն առանձնանում է նրանով, որ չունի հայելային համաչափություն (այն օժտված է միայն պտտական համաչափությամբ), այդ պատճառով է նրա հայելային արտացոլումը կարելի է ստանալ միայն այն շրջելով։ Այն թանգրամի միակ մասն է, որը պետք է շրջենք որոշ ֆիգուրները դասավորելու համար։ Միակողմանի հավաքածուի (որոնցում արգելվում է ֆիգուրները շրջել) օգտագործման ժամանակ կան ֆիգուրներ, որոնք կարելի է դասավորել, իսկ նրանց հայելային պատկերները՝ ոչ։

Պարադոքսներ[խմբագրել | խմբագրել կոդը]

Թանգրամի պարադոքսը հետևյալն է. յուրաքանչյուր անգամ ամբողջությամբ օգտագործելով ամբողջ հավաքածուն՝ կարելի է հավաքել երկու պատկեր, որոնցից մեկը կլինի մյուսի ենթաբազմությունը^[5]։ Այդպիսի մի դեպք վերագրվում է Հենրի Դյուդենիին. նմանատիպ երկու պատկերները ներկայացնում են վանականներ, սակայն նրանցից մեկը ոտք ունի, իսկ մյուսը՝ ոչ^[6]։ Այս պարադոքսի լուծումը ներկայացված է բազմաթիվ աղբյուրներում^[5]։ Լուծումն այն է, որ թվացյալ միանման մասերից կազմված պատկերները ձևով տարբեր են («անոտք» պատկերն ավելի երկար է, քան ոտք ունեցողը), նրանց մակերեսները տարբերվում են «ոտքի» մակերեսի չափով։

Մեկ այլ պարադոքս ներկայացնում է Լոյդն իր «Տանի ութերորդ գիրքը» աշխատության մեջ.

Յոթերորդ և ութերորդ ֆիգուրները ներկայացնում են յոթ մասից կազմված խորհրդավոր քառակուսի։ Այնուհետև քառակուսու անկյունը կտրել են, բայց, այնուամենայնիվ, նորից օգտագործվում են նույն յոթ մասերը^[7]։

Բնօրինակ տեքստ (անգլ.)

The seventh and eighth figures represent the mysterious square, built with seven pieces: then with a corner clipped off, and still the same seven pieces employed.

Այս պարադոսքի լուծումը Լոյդի գրքում տրված չէ։ Այդ գրքի մյուս չլուծված առաջադրանքները քննարկվում են համացանցում^[8];

Դյուդենիի պարադոքս
Լոյդի պարադոքս

Ուրվանկարների հաշվարկ[խմբագրել | խմբագրել կոդը]

Վան Ֆուտրայնն ու Սյուն Ցյուանչժին (熊全治) 1942 թվականին ապացուցել են, որ գոյություն ունի թանգրամի միայն 13 ուռուցիկ ուրվանկար (այնպիսին, որ արտաքին ուրվագծի ցանկացած երկու կետերով անցնող հատվածն անցնում է միայն այդ ուրվագծի մեջ ներառված կետերով) ^[9]^[10]^[11]:

Ռոնալդ Ռիդի «Թանգրամ։ 300 խնդիր» (անգլ.՝ Tangrams: 330 Puzzles) գիրքն ընթերցողներին խնդրում է ուղարկել ցանկացած այլ ֆիգուր։ Այդ պայմանի շնորհիվ թեև ստացվում է՝ տարրերի թիվն ավելանում է այնքանով, որքանով որ ուռուցիկ ֆիգուրները բազմաթիվ են, այնուամենայնիվ դրանք վերջավոր են^[12]։

Ի պատասխան առաջարկվել է մոտավորապես 6,13 միլիոն հնարավոր ուրվանկար^[13], ընդ որում՝ դրանցից յուրաքանչյուրում ցանկացած մասի առնվազն մեկ գագաթը և առնվազն մեկ կողմը համընկնում են մեկ այլ մասի գագաթի և կողմի հետ։

Թանգրամի մանկավարժական դերը[խմբագրել | խմբագրել կոդը]

Նպաստում է կանոններով խաղալու և հրահանգներին հետևելու կարողության, ակնառու-պատկերային մտածողության, երևակայության, ուշադրության, գույները, չափերն ու ձևերն ըմբռնելու, համադրելու ունակությունների զարգացմանը։

Տես նաև[խմբագրել | խմբագրել կոդը]

Մանրահատակ

Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]

↑ Chen, Zhongying (1999). Advances in computational mathematics: proceedings of the Guangzhou international symposium. New York, N.Y: Marcel Dekker. էջեր 466. ISBN 0-8247-1946-8.
↑ Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica Ma, Xiaohe Ma (2003). The Tangram Book. Sterling Publishing Company. ISBN 1-4027-0413-5.{{cite book}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link)
↑ Costello, Matthew J. (1996). The Greatest Puzzles of All Time. New York: Dover Publications. ISBN 0-486-29225-8.
↑ «Tangram» by Enrique Zeleny, Wolfram Demonstrations Project
↑ ^5,0 ^5,1 Tangram Paradox, by Barile, Margherita, From MathWorld — A Wolfram Web Resource, created by Eric W. Weisstein.
↑ Dudeney, H. (1958). Amusements in Mathematics. New York: Dover Publications.
↑ Loyd, Sam (1968). The eighth book of Tan - 700 Tangrams by Sam Loyd with an introduction and solutions by Peter Van Note. New York: Dover Publications. էջ 25.
↑ Unsolved Patterns by Sam Loyd, by Cocchini, Franco, From Tanzzle.com
↑ Fu Traing Wang; Chuan-Chih Hsiung (1942 թ․ նոյեմբեր). «A Theorem on the Tangram». The American Mathematical Monthly. 49 (9): 596–599. doi:10.2307/2303340. Վերցված է 2009 թ․ փետրվարի 6-ին.
↑ Read, Ronald C. (1965). Tangrams : 330 Puzzles. New York: Dover Publications. էջեր 53. ISBN 0-486-21483-4.
↑ А. Панов, Загадка фигуры № 51 // Квант. — 1982. — № 12. — С. 34-37.
↑ Read, Ronald C. (1965). Tangrams : 330 Puzzles. New York: Dover Publications. էջեր 55. ISBN 0-486-21483-4.
↑ Cocchini, F. Ten Millions of Tangram Patterns. TangMath.

Գրականություն[խմբագրել | խմբագրել կոդը]

Anno, Mitsumasa. Anno's Math Games (three volumes). New York: Philomel Books, 1987. 0-399-21151-9 (v. 1), 0-698-11672-0 (v. 2), 0-399-22274-X (v. 3).
Botermans, Jack, et al. The World of Games: Their Origins and History, How to Play Them, and How to Make Them (translation of Wereld vol spelletjes). New York: Facts on File, 1989. 0-8160-2184-8.
Dudeney, H. E. Amusements in Mathematics. New York: Dover Publications, 1958.
Gardner, Martin. "Mathematical Games—on the Fanciful History and the Creative Challenges of the Puzzle Game of Tangrams", Scientific American Aug. 1974, p. 98–103.
Gardner, Martin. "More on Tangrams", Scientific American Sep. 1974, p. 187–191.
Gardner, Martin. The 2nd Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon & Schuster, 1961. 0-671-24559-7.
Loyd, Sam. Sam Loyd's Book of Tangram Puzzles (The 8th Book of Tan Part I). Mineola, New York: Dover Publications, 1968.
Slocum, Jerry, et al. Puzzles of Old and New: How to Make and Solve Them. De Meern, Netherlands: Plenary Publications International (Europe); Amsterdam, Netherlands: ADM International; Seattle: Distributed by University of Washington Press, 1986. 0-295-96350-6.
Танграм // Занимательные головоломки. — Де Агостини, 2012. — № 5. — С. 13—16.

Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]

Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Թանգրամ» հոդվածին։

[isbn0-8247-1946-8-1] Chen, Zhongying (1999). Advances in computational mathematics: proceedings of the Guangzhou international symposium. New York, N.Y: Marcel Dekker. էջեր 466. ISBN 0-8247-1946-8.

[isbn1-4027-0413-5-2] Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica Ma, Xiaohe Ma (2003). The Tangram Book. Sterling Publishing Company. ISBN 1-4027-0413-5.{{cite book}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link)

[isbn0-486-29225-8-3] Costello, Matthew J. (1996). The Greatest Puzzles of All Time. New York: Dover Publications. ISBN 0-486-29225-8.

[4] «Tangram» by Enrique Zeleny, Wolfram Demonstrations Project

[mathematica-5] 5,0 ^5,1 Tangram Paradox, by Barile, Margherita, From MathWorld — A Wolfram Web Resource, created by Eric W. Weisstein.

[dudeney-6] Dudeney, H. (1958). Amusements in Mathematics. New York: Dover Publications.

[loyd-7] Loyd, Sam (1968). The eighth book of Tan - 700 Tangrams by Sam Loyd with an introduction and solutions by Peter Van Note. New York: Dover Publications. էջ 25.

[unsolved_patterns-8] Unsolved Patterns by Sam Loyd, by Cocchini, Franco, From Tanzzle.com

[9] Fu Traing Wang; Chuan-Chih Hsiung (1942 թ․ նոյեմբեր). «A Theorem on the Tangram». The American Mathematical Monthly. 49 (9): 596–599. doi:10.2307/2303340. Վերցված է 2009 թ․ փետրվարի 6-ին.

[isbn0-486-21483-4-10] Read, Ronald C. (1965). Tangrams : 330 Puzzles. New York: Dover Publications. էջեր 53. ISBN 0-486-21483-4.

[11] А. Панов, Загадка фигуры № 51 // Квант. — 1982. — № 12. — С. 34-37.

[isbn0-486-21483-4_b-12] Read, Ronald C. (1965). Tangrams : 330 Puzzles. New York: Dover Publications. էջեր 55. ISBN 0-486-21483-4.

[tangmath-13] Cocchini, F. Ten Millions of Tangram Patterns. TangMath.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]