Բնության օրինաչափություններ


Բնության օրինաչափություններ, բնական պայմաններում ձևավորվող կրկնվող այս կամ այն ձևերն են և նրանց համադրությունները։ Դրանք դրսևորվում են բնության տարբեր օբյեկտներում և երևույթներում, երբեմն էլ կարող են նկարագրվել մաթեմատիկական մոդելներով։
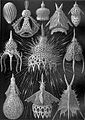
Բնության մեջ կրկնվող ձևերը լինում են տարբեր ձևերի՝ դրսևորվելով սիմետրիաներում, ծառերում, գալարներում, գետերի կորաձև թեքումներում, ալիքներում, փրփուրներում, երկրաչափական նախշերում և այլն[1][2]։ Դեռևս հին հույն առաջին փիլիսոփաները՝ Պլատոնը, Պյութագորասը, Էմպեդոկլեսը, ուսումնասիրել են տվյալ օրինաչափությունները՝ փորձելով բացատրել բնական կարգը։ Սակայն դարեր են պահանջվել, որ կրկնման այդ օրինաչափությունների ժամանակակից ընկալումը սահմանվի։ Այսպես՝ գերմանացի կենսաբան և նկարիչ Էռնստ Հեկկելը նկարեց ծովային հարյուրավոր օրգանիզմներ, որպեսզի ապացուցի դրանց մեջ եղած համաչափությունը։ Շոտլանդացի կենսաբան Դարսի Թոմփսոնը առաջինը ուսումնասիրեց բույսերի և կենդանիների աճի օրինաչափությունները։
Մաթեմատիկան, ֆիզիկան և քիմիան բացատրում են բնության օրինաչափությունները տարբեր մակարդակներում։ Կենդանի բնության օրինաչափությունները բացատրվում են բնական և սեռական ընտրության կենսաբանական գործընթացներով։ Օրինաչափությունները ուսումնասիրելիս հաճախ օգտագործվում է համակարգչային մոդելավորման եղանակը։
Պատմություն[խմբագրել | խմբագրել կոդը]

Հին հույն փիլիսոփաները փորձել են նկարագրել և բացատրել բնության օրինաչափությունները՝ նախանշելով ժամանակակից գաղափարները։ Իր աշխատություններում (427-347) Պլատոնը նշել է գոյություն ունեցող ընդհանրությունների մասին։ Նա ենթադրել է, որ դրանք անթերի են, իսկ ֆիզիկական օբյեկտները՝ դրանց ոչ կատարյալ կրկնօրինակները։ Այդպիսով՝ ծաղիկը կարող է կլորավուն լինել, բայց դա երբեք չի լինի կատարյալ շրջանաձև։ Պյութագորասը բնության օրինաչափությունները դիտարկում էր այնպես, ինչպես հարմոնիան երաժշտության մեջ, որ սկսվում է թվից, ինչպես ի սկզանե ամեն ինչ[3]։
1202 թվականին Լեոնարդո Ֆիբոնաչին (1170-1250) իր «Հաշվեգրքում» բացահայտեց թվերի հետաքրքիր հերթագայությունը[4]։ Ֆիբոնաչին բերում է ճագարների գլխաքանակի աճի կենսաբանական օրինակը[5]։ 1917 թվականին Դարսի Թոմփսոնը հրատարակում է «Աճի և ձևի մասին» իր գիրքը։ Ֆիլոտաքսիսի (տերևների դասավորվածությունը ցողունի վրա) և Ֆիբոնաչիի թվերի միջև առկա կապի նկարագրությունը դարձել է դասական օրինակ։ Նա ցույց տվեց, որ հասարակ հավասարումներով կարող են նկարագրվել կենդանիների պոզերի աճի կամ փափկամարմինների խեցիների զարգացման առերևույթ ավելի բարդ օրինաչափությունները[6]։
Գերմանացի հոգեբան Ադոլֆ Ցեյզինգը պնդում էր, որ ոսկե հատումը դիտարկվում է բույսերի մասերի, կենդանիների կմախքների, երակների և նյարդաթելերի դասավորվածության մեջ, ինչպես նաև բյուրեղի կառուցվածքում[7][8][9]։

Էռնստ Հեկկելը (1834-1919) հրատարակել է ծովային տարբեր կենդանիների, հատկապես ճառագայթավորների պատկերներով գիրք՝ ընդգծելով դրանց համաչափությունը։
Ամերիկացի լուսանկարիչ Ուիլսոն Բենթլին 1885 թվականին կատարել է ձյան փաթիլի առաջին միկրոնկարը։
1952 թվականին Ալան Թյուրինգը, որ մեծ հռչակ էր ձեռք բերել հաշվողական տեխնիկայի բնագավառում իր աշխատանքներով, գրեց «Մորֆոգենեզի քիմիական հիմքը» հոդվածը, որում վերլուծում էր այն մեխանիզմները, որոնք անհրաժեշտ են կենդանի օրգանիզմներում օրինաչափոթյունների առաջացման համար. դա, այսպես կոչված, մորֆոգենեզն է։ Նա կանխագուշակել է քիմիական ռեակցիաների տատանումները՝ մասնավորապես Բելոուսով-Ժաբոտինսկու ռեակցիան։
Պատճառներ[խմբագրել | խմբագրել կոդը]

Կենդանի օրգանիզմները, ինչպես օրինակ կոլիբրին, սիրամարգի պոչը, ունեն ունեն նախշերի և գույների գեղեցիկ աբստրակտ ձևեր[10]։ Գեղեցկությունը, որ մարդիկ տեսնում են բնության մեջ, հիմնավորված է տարբեր մակարդակներում, մասնավորապես մաթեմատիկայում, որը նկարագրում է օրինաչափությունների ֆիզիկական կողմը նաև կենդանի օրգանիզմների միջավայրում, ուր ամեն ինչ որոշում է բնական ընտրությունը։
Մաթեմատիկայի մեջ ձգտում են բացահայտել և բացատրել բոլոր տեսակների կառուցվածքի աբստրակտ օրինաչափությունները[11]։ Բնության ակնհայտ օրինաչափությունները բացատրվում են քաոսի տեսությամբ, ֆրակտալներով, լոգարիթմական պարույրներով[12]։
Ֆիզիկայի օրենքներում աբստրակտ մափեմատիկան կիրառվում է իրական աշխարհում։ Օրինակ՝ բյուրեղը իդեալական է համարվում, երբ այն չունի կառուցվածքային թերություններ և համաչափ է։ Մաթեմատիկական կատարելությունը կարող է միայն երբեմն մոտ լինել իրական օբյեկտներին. բնության օրինաչափությունները ենթարկվում են ֆիզիկական օրենքներին։
Կենսաբանության մեջ բնական ընտրությունը կարող է նպաստել կենդանի օրգանիզմներում բնական օրինաչափությունների զարգացմանը գունավորման, միմիկրիայի, սիմբիոզի պատճառներով[13]։ Բույսերի ձևը, գույնը, ծաղկի տեսակը կարող են փոփոխվել՝ օրինակ, փոշոտման նպատակով միջատներին գրավելու նկատառումով։ Միջատներ կան, որոնց գրավում են ճառագայթաձև նախշավորում ունեցող բույսերը, ծաղիկների քաղցր փոշին, նեկտարը[14]։
Օրինաչափությունների տեսակներ[խմբագրել | խմբագրել կոդը]

Համաչափություն[խմբագրել | խմբագրել կոդը]
Համաչափությունը տարածված է կենդանի բնության մեջ։ Կենդանիների շրջանում, ինչպես բույսերի տերևների, որոշ ծաղիկների (օրինակ՝ խոլորձ) մոտ, տարածված է երկկողմանի կամ հայելային համաչափությունը։ Բույսերը ավելի հաճախ ունենում են ճառագայթային կամ շրջանաձև համաչափություն։ Այդ համաչափությամբ օժտված են նաև կենդանիների որոշ տեսակներ։ Հնգահամաչափությունը հանդիպում է փշամորթների շրջանում (ծովային աստղեր, ծովոզնիներ)[15]։
Անկենդան բնության մեջ վեցակի համաչափությամբ են օժտված ձյան փաթիլները. նրանցից յուրաքանչյուրն ինքնատիպ է, իսկ դրանց ձևը բյուրեղացման պայմանների փոփոխությամբ է պայմանավորված[16]։ Բյուրեղներն ունեն համաչափության տարբեր ձևեր և արտաքին տեք. նրանք կարող են լինել խորանարդաձև, ութանիստ, բայց իսկական բյուրեղները չեն կարող լինել հնգահամաչափ՝ ի տարբերություն կվազիբյուրեղների։
Շրջանաձև համաչափությունը հանդիպում է անկենդան բնության մեջ ամենատարբեր չափերով՝ սկսած ներքև ընկնող կաթիլի հետքից մինչև Սատուրնի՝ հսկայական չափեր ունեցող օղակները[17]։
Համաչափությունը կարող է ունենալ տարբեր պատճառներ ու հիմքեր։ Կենսաբանության մեջ ճառագայթաձև համաչափության մասին խոսվում է, երբ եռաչափ էակի միջով անցնում է համաչափության մեկ կամ ավելի առանցք։ Այդ դեպքում կենդանիների համաչափությունը կարող է հարթ չլինել։ Օրինակ՝ Velella velella հիդրոիդը ունի համաչափության երկրորդ կարգի առանցք, բայց չունի հարթ համաչափություն[18]։ Ճառագայթային համաչափությունը բնորոշ է փշամորթներին։ Դրանց մեջ հանդիպում է հնգահամաչափությունը։ Վաղ շրջանում փշամորթներն ունեցել են հայելային համաչափություն։ Սամրելը և Ռեյը պնդում են, որ համաչափության հին ձևի կորուստը կատարվել է բնական և էվոլյուցիոն պատճառներով[19]։
Բացի ճառագայթային համաչափության տարածված տեսակից՝ գոյություն ունի երկակի ճառագայթային համաչափություն (գործում է համաչափության երկու հարթություն, օրինակ՝ սանրակիրներ)։
Ծաղկավոր բույսերը հաճախ ունենում են ճառագայթաձև համաչափությամբ ծաղիկներ՝ համաչափության 3,4,5,6 հարթություններով։ Կենդանական աշխարհում երկկողմանի համաչափության առաջացումը կապված է տեսակների զարգացման հետ, որի արդյունքում ձևավորվել են ողնաշարավորների մարմնի աջ և ձախ մասերը, չնայած ներքին օրգանները կարող են լինել անհամաչափ։ Ընդհանուր առմամբ, կենդանական աշխարհում երկկողմ համաչափությունը առավելապես դրսևորվել է ակտիվորեն շարժվող տեսակների մոտ։ Բույսերի կառուցվածքում երկկողմ համաչափությունը դրսևորվում է միայն որոշ մասերում, օրինակ՝ տերևներում կամ ծաղիկներում։
-
Կենդանիներն ամենից շատ ունեն հայելային համաչափություն, ինչպես այս վագրը
-
Փշամորթները, օրինակ՝ ծովաստղերը, հնգահամաչափ են
-
Հնգահամաչափությունը հանդիպում է շատ ծաղիկների, մրգերի մոտ, օրինակ՝ զկեռնի գերմանական
-
Փաթիլն ունի երկհամաչափություն
-
Ամեն փաթիլ յուրօրինակ է, բայց ունի համաչափություն
-
Կալցիումի ֆտորիդի բյուրեղը խորանարդաձև է
-
Ջրի ցայտքերը ճառագայթային համաչափություն ունեն
-
Նռնաքարերի բյուրեղներն ունեն դոդեկաեդրի համաչափություն
-
Վոլվոքսն ունի գնդաձև համաչափություն
-
Ակտինիաներն ունեն առանցքային համաչափություն
Բույսեր և ֆրակտալներ[խմբագրել | խմբագրել կոդը]

Ֆրակտալները մաթեմատիկական կառուցվածքի համանման անվերջ կրկնվող փուլեր են[20] [21] [22]: Ֆրակտալները անվերջ նման են իրար։ Սակայն բնության մեջ հնարավոր չէ անվերջ կրկնություն։ Այդ պատճառով բնության մեջ օրինաչափ կրկնությունները մոտ են ֆրակտալներին։ Օրինակ՝ հովանոցավորների տերևները նմանատիպ են երկրորդ, երրորդ, չորրորդ մակարդակներում։ Նման կառուցվածք ունեն շատ այլ բույսեր ևս՝ բրոկկոլին, կաղամբը, արքայախնձորը, ծառապսակները, տերևները, ինչպես նաև կենդանիներ՝ կորալներ, ջրային պարզագույն կենդանիներ, ծովաստղեր, ծովոզնիներ։ Ֆրակտալների ձևը դրսևորվում է մարդու արյունատար համակարգում (արյունատար անոթներ) և մարդկանց ու կենդանիների թոքերում[23]։
Ֆրակտալների՝ Լանդերմայերի համակարգը կարող են մոդելավորել ծառերի աճը՝ փոփոխելով ոչ մեծ թվով պարամետրեր, այդ թվում՝ թեքության աստիճանը, ցողունի երկարությունը[24]։
Նման ֆրակտալները լայն տարածում ունեն բնության մեջ։ Դրանց դրսևորման օրինակ են ամպերը, էլեկտրական լիցքերը, գետային ցանցերը, լեռնաշղթաները, ափագծերը, կենդանիների գունավորումը, ձյան փաթիլները, սառնամանիքից ապակու վրա առաջացող նախշերը, բյուրեղները, արյունատար անոթները, ծովային ալիքները և այլն[25][26]։
-
Հովանոցավոր բույսի տերևներ
-
Ֆրակտալ տերևներ, բրոկկոլի
-
Բոխնի. ծաղիկը կազմված է համանման գնդաձև մասերից
-
Ծառեր. դենդրիտային բյուրեղները մանրադիտակով դիտելիս
Պարույր[խմբագրել | խմբագրել կոդը]

Պարույրի ձևը տարածված է բուսական աշխարհում և մի քանի կենդանատեսակների, օրինակ փափկամարմինների շրջանում։ Նավախեցիների մոտ յուրաքանչյուր խեցի նախորդի կրկնությունն է, որ դասավորված է պարույրի լոգարիթմով։
Փորոտանիների մեծամասնության խեցին պարույրաձև է, ընդ որում պարույրի պտույտները ավելի շատ տարբեր հարթություններում են։ Նման պարույրը կոչվում է հելիկոիդ։ Այսպիսի պարույր ունեցող տեսակների մեծամասնության մոտ գալարները ժամացույցի ուղղությամբ են ձգվում, հազվագյուտ տեսակներում՝ ժամացույցի սլաքի հակառակ ուղղությամբ[27][28]։
Բույսերի շրջանում պարույրները դրսևորվում են ցողուններին տերևների, ծաղկի սերմերի դասավորվածության մեջ, օրինակ՝ արևածաղկի սերմեր, արքայախնձորի պտուղ, եղևնու կոն, որտեղ պարույրները դասավորված են ինչպես ժամացույցի սլաքի ուղղությամբ, այնպես էլ՝ հակատակ[29]։ Այս մեխանիզմները բացատրվում են և՛ մաթեմատիկական, և՛ ֆիզիկական, և՛ քիմիական , և՛ կենսաբանական մակարդակներում, որոնցից յուրաքանչյուրը ճիշտ է, բայց կարևոր է բոլորի ուսումնասիրությունը[30]։

Մաթեմատիկական տեսանկյունից պարույրի ձևը կարող է մոդելավորվել Ֆիբոնաչիի թվերի սկզբունքով, երբ ամեն թիվը հավասար է նախորդ երկուսի գումարին՝ 1, 1, 2, 3, 5, 8, 13 և այլն։ Օրինակ, երբ տերևները աճում են ցողունին, պարույրի մեկ շրջանը ընդգրկում է երկու տերև, այսինքն՝ հարաբերությունն է 1/2: Տիզենու տերևների հարաբերությունը 1/3 է, ծիրանենունը՝ 2/5, տանձենունը՝ 3/8, նշենունը՝ 5/13[31]: Երիցուկի սկավառակում, ինչպես և արևածաղկի թերթիկները դասավորված են Ֆերմայի պարույրով՝ Ֆիբոնաչիի թվերի սկզբունքով[32]։
Ֆիզիկայի տեսանկյունից պարույրը ցածր էներգետիկա ունի, որը պայմանավորված է դինամիկ համակարգի ինքնակառավարվող գործընթացներով[33]։
Քիմիական տեսանկյունից պարույր կարող է ձևավորվել դիֆուզային ռեակցիայով՝ ինչպես ուժեղացող, այնպես էլ թուլացող։ Այն կառավարվում է պրոտեիններով, որոնք կարգավորում են բուսական աուքսին հորմոնի խտությունը, որն ակտիվացնում է բույսի միջին ցողունի աճը։
Կենսաբանական տեսանկյունից տերևները դասավորված են այնպիսի հեռավորության վրա, ինչպիսին թույլ է տալիս բնական ընտրությունը, քանի որ ֆոտոսինթեզի համար տերևները ձգտում են բնական ռեսուրսներին, մասնավորապես արևի ջերմությանը[29]։
-
Ֆիբոնաչիի պարույրը
-
Խոյ Ovis canadensis
-
Հալվեի պարույրը
-
Նավախեցիների խեցի
-
Ֆերմայի պարույրը արևածաղկի Helianthus annuus ծաղիկում
-
Ֆիբոնաչիի պարույրների բազմություն կաղամբի կտրվածքում
-
Trochoidea liebetruti փորոտանու խեցու վրա երևում են նրա աճի հետքերը
Քաոս, հոսանք, ոլորապտույտ[խմբագրել | խմբագրել կոդը]
Ինչպես ֆրակտալները, քաոսի տեսությունը ևս բնության օրինաչափությունների վրա ազդող միջոցներից է։ Կա փոխադարձ կապ քաոսի և ֆրակտալների միջև. քաոսային համակարգի ձգումներն ունեն ֆրակտալի չափեր[34]։
Հորձանուտի ճանապարհը հորձանքի զիգզագաձև պտույտն է, որ առաջանում է հեղուկի հոսանքի ոչ ստանդարտ բաժանումից. դա կարող է լինել քամու կամ ջրի հետևանքով[35]։ Հարթ հոսանքը սկսում է քայքայվել, երբ հոսանքի չափը կամ արագությունը մեծանում է։
Ոլորապտույտը երկրաչափական դրվագի՝ կոտրված գծի տեսք ունի։ Բնության մեջ ոլորապտույտը ամենից շատ հանդիպում է գետերի հոսքի հետագծում։ Հենց գետի հունը թեթևակի պտտվում է, մեծանում է նրա չափն ու թեքությունը, քանի որ ժապավենաձև պտույտը իր հետ տանում է ավազ ու հող գետի թեքման ներքին ուղղությամբ։ Դրա հետևանքով էրոզիան արագանում է, որը հակադարձ կապով հանգեցնում է ոլորապտույտի մեծացման[36]։ Ոլորապտույտի ներքին ափն ավելի մեղմ է, քան արտաքին ափը։ Սրանով հանդերձ՝ գետը կարող է երկար ժամանակ տեղափոխել ալիքները՝ պահպանելով հունի սինուսոիդ ձևը։
-
Խեցու քաոսային գունավորում
-
Հսկայական հորձանուտային ճանապարհ ամպերում, լուսանկար արբանյակից
-
Ոլորապտույտ Ռիո Նեգրո գետի հովտում, լուսանկար արբանյակից
-
Ոլորապտույտ, սողացող օձ
-
Ուղեղի համաչափ գալարներ Diploria strigosa
Ալիքներ, դյուներ[խմբագրել | խմբագրել կոդը]
Ալիքները շարժման ընթացքում տեղափոխում են էներգիա։ Մեխանիկական ալիքները տարածվում են օդով կամ ջրով՝ ստիպելով նրանց տատանվել[37]։ Քամու ալիքները ծովի մակերևույթի ալիքներն են, որոնք ստեղծում են բնորոշ քաոսային պատկեր, չնայած նրանց[38] ստատիկ վարքը կարող է նախատեսվել մոդելներով։ Երբ ալիքները ջրում կամ օդում բախվում են ավազի, նրանք ստեղծում են թմբեր։ Երբ քամին փչում է ավազուտ մակերևույթին, առաջանում են դյուներ, որոնք կարող են ձևավորել բավական մեծ տարածքներ, ինչպես Տակլա Մական անապատում։ Դյուները կարող են ձևավորել օրինաչափությունների շղթա՝ ներառյալ կիսալուսինը, շատ երկար գծերը, աստղերը, պարաբոլները, երկայնական ձևերը[39]։ Դյուների առանձնահատկությունը նրա շարժն է քամու՝ ավազը քշելու հաշվին։ Մշտական ուժեղ քամիների արդյունքում էլ կատարվում է շարժումը։ Դյուների շարժման արագությունը կարող է կազմել տարեկան 20մ։
Քամու ռեժիմից կախված՝ ավազաթմբերը տարբեր տեսք են ունենում։ Օրինակ՝ լինում են ավազաթմբեր, որոնք ձգվում են երկայնակի՝ քամու ուղղությանը զուգահեռ, լինում են և ավազաբուրգեր. ավազը հավաքվում է հակառակ կողմից՝ հորիզոնի գծի հետ կազմելով 15° անկյուն։ Այդ դեպքում ավազը կուտակվում է քամու կողմից և կարող է կազմել մինչև 35°: Երբ ավազակույտի անկյունը գերազանցում է լանջի անկյունը, ավազը սկսում է թափվել. ոչ մեծ քանակությամբ ավազի կուտակումը անհետևանք կարող է անցնել, մինչդեռ ավազի անընդհատ ավելացումը կարող է հանգեցնել ավազաթմբի քանդման[40]։ Ավազաթմբերը իրենց դրսևորում են այնպես, ինչպես սովորական ալիքները[41]։
-
Ալիքը «կոտրվում» է
-
Ավազի դյուներ Տակլա Մական անապատում
-
Ավազակույտի սխեմա
Պղպջակ, փրփուր[խմբագրել | խմբագրել կոդը]
Օճառի պղպջակը գունդ է, որի մակերևույթը ունի փոքր մակերես։ Երկու պղպջակ միավորվելով կազմում են ավելի բարդ ձև. երկու պղպջակների արտաքին մակերևույթները ունենում են գնդի ձև, որոնք միավորվում են գնդաձև երրորդ մակերևույթով, որը ձձավորվում է փոքր գնդի՝ մեծին հենվելու արդյունքում։
Փրփուրը պղպջակների բազմությունն է։ Բնության մեջ գոյություն ունեն տարբեր նյութերի փրփրադեզեր։ Օճառի պղպջակները ենթարկվում են Պլատոյի օրենքին, որի համաձայն՝ պղպջակները միանում են 120° անկյան տակ։ Չորս պղպջակները միանում են տետրաեդրի տեսքով 109.5° անկյամբ։ Պլատոյի օրենքը ենթադրում է, որ պղպջակները լինեն հարթ մակերևույթներով և ունենան մշտական միջին թեքություն ամեն կետում։
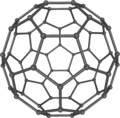
Փրփուրի օրինաչափությունները հաճախ են հանդիպում կենդանի բջիջների աշխարհում. ճառագայթավորները, սպունգները, ծովոզնիների էկզոկմախքը ասվածի վկայությունն են։ Ճառագայթավորներից Aulonia hexagona-ի կմախքը, որ նկարագրել է Հեկկելը, այնպիսի տեք ունի , կարծես գունդը ամբողջությամբ կազմված է վեցանկյուններից, բայց դա մաթեմատիկորեն անհնար է։ Էյլերի բնութագիրը վկայում է, որ յուրաքանչյուր ուռուցիկ բազմանիստի կողմերի և գագաթների գումարի քանակը հավասար է եզրերի թվին գումարած երկու։ Այս բանաձևի արդյունքն այն է, որ վեցանկյուններից կազմված յուրաքանչյուր փակ բազմանիստ պետք է պարունակի ճիշտ 12 հնգանկյուն, ինչպես ֆուտբոլի գնդակը կամ ֆուլերենի մոլեկուլը։ Սա կարելի է պատկերացնել վեցանկյուններից կազմված հարթ ցանցի տեսքով, որը ավելացող ամեն հնգանկյան հետ թեքվում է։
-
Օճառի պղպջակների փրփուր. չորս պղպջակներ միանում են 109.5° անկյան տակ, ինչպես մեթանի մոլեկուլում C-H կապը
-
Ճառագայթավորներ, նկար Հեկկելի գրքից (1904)
-
Ճառագայթավոր Spumellaria. այս տեսակի կմախքը ունի փրփուրի ձև
-
Ֆուլերինի սինթեզված մոլեկուլ
-
Կրկեսային վրանները ունեն մինիմալ մակերևույթ
-
Պեկինի՝ ջրային մարզաձևերի կենտրոնի արտաքին պատը Վաերա-Ֆելենի կառուցվածքով
-
Գազի պղպջակների մակերևույթի հավասար գնդեր
Խճանկար[խմբագրել | խմբագրել կոդը]

Խճանկարը օրինաչափություն է, որը ձևավորվում է հարթ մակերևույթին բաղադրիչ տարրերի անընդհատ կրկնումից։ Կա խճանկարի 17 տեսակ[42]։ Չնայած խճանկարը տարածված է արվեստում և դիզայնի մեջ, սակայն այն գրեթե չի հանդիպում կենդանի օգանիզմներում։ Խճանկարի օրինակ են կրետների բները, մեղրամոմը։ Կենդանի օրգանիզմներում խճանկարի դրսևորման օրինակ են ձկների թեփուկները, պանգոլինների մաշկի երկրորդական ոսկրացումը։ Դրանք այս կամ այն ճշգրտությամբ կրկնվող միավորներից են բաղկացած, չնայած իրականում նրանց չափերը տատանվում են։ Բույսերի շրջանում խճանկարի դրսևորման օրինակ են սալակ միրգը, շախմատաձև արքայապսակը, որի թերթիկներին շախմատի տախտակի խճանկարային պատկեր է։
Միներալների կառուցվածքը համաչափ կկնվող եռաչափ խճանկարի լավ օրինակ է։ Հարյուր հազարավոր միներալների մեջ կան ատոմների դասավորության բավական քիչ տեսակներ` բյուրեղի կառուցվածք ունեցող։
Բնության մեջ խճանկարի դրսևորման օրինակ է բնության հուշարձան Հսկաների ճանապարհը, որը կազմված է իրար կապված մոտ 40.000 բազալտե սյուներից, որոնք ձևավորվել են հրաբուխի ժայթքման արդյունքում[43]։ Սյուների մեծամասնությունը վեցանկյուն է, չնայած կան 4, 5, 7, 8 անկյուն ունեցող սյուներ ևս։ Մոտ 50-60 միլիոն տարի առաջ` պալեոգենի շրջանում, ժայթքել է հրաբուխը; Երբ հոսել է հալված բազալտը, ձևավորվել է լավայի հարթակ։ Արագ սառեցման արդյունքում ծավալի կրճատում է եղել. հորիզոնական սեղմումը հանգեցրել է վեցանկյուն սյուների առաջացմանը[44]։
-
Բյուրեղներ, հալիտի խորանարդաձև բյուրեղ
-
Մեղրամոմ. բնական խճանկարի օրինակ
-
Շախմատաձև արքայապսակի ծաղիկը
-
Խճանկարը ձկան թեփուկներում
-
Սալակ Salacca zalacca մրգի կեղևը
-
Խճանկարով մայթ, Թասմանի թերակղզի
Ճաքեր[խմբագրել | խմբագրել կոդը]
Ճաքերը գծային բացվածքներ են, որոնք առաջանում են տարբեր նյութերում լարման նվազման արդյունքում։ Երբ էլաստիկ նյութը հավասարապես ձգվում է, հասնում է իր սահմաններին և հանկարծակի կոտրվում տարբեր ուղղություններով՝ առաջացնելով ճաքեր։ Եվ հակառակը, երբ ոչ էլաստիկ նյութը ջարդվում է, առաջանում են ճաքեր՝ թուլացնելով լարումը։ Ուղիղ անկյամբ ճնշումը կարող է նոր ճաքերի առաջացման առիթ հանդիսանալ։ Այսպիսով՝ ճաքերի պատկերը ցույց է տալիս՝ նյութը էլաստի՞կ է, թե՞ ոչ[45]։ Ամուր հյուսվածքով նյութերում (օրինակ՝ կաղնու փայտ) առաջանում են ճաքեր, որ լարումը թուլանա, բայց դրանք չեն մեծանում ժամանակի ընթացքում։ Ինչպես փայտի ամեն տեսակ ունի բջջային և մոլեկուլային յուրահատուկ կառուցվածք, այնպես էլ յուրաքանչյուր ծառ ունի ճաքերի իր պատկերը[46]։
-
Հին կերամիկայի մակերևույթ. ճաքերը ձևավորվել են 90° անկյան տակ
-
Չորացած ցեխ
-
Չորացած էլաստիկ ցեխ Սիցիլիայում՝ ձևավորված 120° անկյան տակ
-
Հսկաների ճանապարհի վեցանկյուն սյուները. բնության հուշարձան
-
Արմավենու բունը հորիզոնական ճեղքերով
Պուտեր ու բծեր[խմբագրել | խմբագրել կոդը]

Շատ կենդանիներ ունեն մարմնի պուտավոր (ընձառյուծ, զատկաբզեզ) և գծավոր գունավորում (վագր, զեբր)։ Այդպիսի գունավորումը միացնող կամ քայքայող տպավորություն կարող է թողնել։ Վերջինս խանգարում է մարմնի ուրվագծերը ընկալելու տեսողական տպավորությունը. այդ պատճառով կենդանիները մնում են աննկատ իրենց շրջապատող միջավայրի ֆոնին[47]։ Քողարկման արդյունավետությունն ավելի է մեծանում, երբ գունավորման որոշ հատվածներ իրենց գույնով ու ձևով ամբողջովին համընկնում են շրջակա ֆոնին։ Կան կենդանիներ, որոնց գունավորումը, ընդհակառակը, առանձնանում է շրջապատի ֆոնից։ Պուտավոր ու բծավոր գունվորումը որոշ կենդանիների թույլ է տալիս պաշտպանվել թշնամուց (կորալյան պոլիպների մջ ապրող ձկներ), մյուսներին էլ թույլ է տալիս աննկատ մոտենալ զոհին (ընձառյուծ, վագր)։ Այսպիսի գունավորումը հաճախ գիշատիչների և նրանց զոհերի հարմարվողականության արդյունք է՝ ձևավորված էվոլյուցիայի ընթացքում։
Պուտավոր և բծավոր գունավորումը կարող է զգուշացնող նշանակություն ունենալ[48]։ Այն բնորոշ է թունավոր տեսակներին, որոնք առանձնանում են նաև վառ գունավորումով։ Օրինակ՝ զատկաբզեզը ավելի քիչ է ենթարկվում թռչունների հարձակմանը, եթե ունենում է վառ գունավորում[49]։ Անփորձ թռչունը, տեսնելով զատիկի զգուշացնող գունավորումը, կարող է փորձել ուտել միջատին, բայց դա անում է մեկ անգամ. տհաճ համով զատիկից ազատվելու համար թռչունը կարող է անգամ թքել։ Արդյունքում թռչունը խուսափում է հաջորդ անգամ այս միջատին ուտելուց։ Փորձի կուտակումը ամեն սերունդ ինքնուրույն է կատարում՝ հաշվի առնելով իր «համտեսումներն ու սխալները»[50]։
Կենդանիները, լինի զոհ թե գիշատիչ, որոնք ժառանգել են պուտերի գեները, կենսունակ են։ Էվոլյուցիոն և գործառական առումներով կարելի է բացատրել, թե ինչու են առաջանում պուտեր, բայց դժվար է բացատրել, թե ինչ օրինաչափությամբ են ձևավորվում դրանք։
-
Conus litteratus-ի խեցիներ
-
Colobura dirce թիթեռ
-
Արքայական հրեշտակ Pygoplites diacanthus
Օրինաչափությունների ձևավորում[խմբագրել | խմբագրել կոդը]
Ալան Թյուրինգը և մաթեմատիկական կենսաբան Ջեյմս Մարին նկարագրել են այն մեխանիզմը, որի արդյունքում տարերայնորեն առաջանում են պուտավոր կամ բծավոր նախշեր[51]։ Երիտասարդ օրգանիզմի բջիջներն ունեն գեներ, որոնք կարող են աշխատել քիմիական ռեակցիայի մակարդակով։ Դա մորֆոգենն է, որ հանգեցնում է որոշակի հատկությունների ձևավորմանը (օրինակ՝ մուգ պուտերի առաջացում)։ Եթե մորֆոգենը առկա է ամենուր, ապա արդյունքում առաջանում է այնպիսի գունավորում, ինչպիսին սև ընձառյուծինն է։ Բայց եթե այն բաշխված է անհամաչափ, արդյունքում ձևավորվում են պուտեր կամ բծեր։ Թյուրինգը ենթադրում էր, որ միգուցե հնարավոր է մորֆոգենի ստեղծման հակադարձ կապը, ինչը կարող է հանգեցնել մորֆոգենի ծավալի մշտական տատանումների։
Հետագա ուսումնասիրությունները թույլ տվեցին ստեղծել տարբեր օրինաչափությունների համոզիչ մոդելներ, ինչպիսիք են ընձուղտի պուտերը, զեբրի բծերը[52]։ Ռիչարդ Պրամի մոդելները, որոնք ստեղծվել են Թյուրինգի հետազոտությունների հիման վրա, վեց փոփոխականների միջոցով բացատրում են գունավորման ինը հիմնական օրինաչափությունների սկզբունքը՝ պարզից բարդ[53]։ Ավելի բարդ մոդելները ընդօրինակում են թռչունների թևերի բարդ նախշերը, երբ առանձին փետուրներ ունեն գունային անցումներ։ Նրանք հաշվի են առնում տատանումը, որը պայմանավորված է տարածությամբ ու ժամանակով[54]։
Օրինաչափություններ կարող են ձևավորվել նաև լանդշ աֆտներում[55][56]։ Օրինակ՝ վագրային լանդշաֆտը ձևավորվում է չոր լանջերին, որտեղ բույսերի աճը սահմանափակված է անձրևային տեղումների ցածր մակարդակով։ Հորիզոնական ամեն մի շերտ արդյունավետ հավաքում է անձրևաջուրը հարևանությամբ գտնվող դատարկ հատվածից[55]։
Փշատերև անտառներում ալիքները ձևավորվում են թեք լանջերին քամու ավերիչ ուժի հետևանքով։ Ընկնող ծառերի հարևանությամբ գտնվող ծառերը ավելի շատ են ենթակա վնասի, հետևաբար բաց տարածքները առաջանում են քամու ուղղությամբ։
Բնական նախշեր կարող են առաջանալ կենդանիների կենսագործունեության արդյունքում, ինչպես ԱՄՆ-ի հյուսիսարևմտյան նահանգներում առաջացել են կրծողների երկարամյա գործունեության արդյունքում[57]։
Հավերժական սառույցով ծածկված մասերում ամենամյա սառեցման և հալեցման արդյունքում առաջանում են գծեր, շրջաններ, ցանցեր, սանդղանման մակերևույթներ։ Բարձր ջերմության արդյունքում կարող են առաջանալ ճաքեր, որոնք հալոցքի ժամանակ լցվում են ջրով, իսկ սառեցման ժամանակ խորանում են[58]։
-
Մբու ձուկ Tetraodon mbu
-
Ֆուգու ձկան կաշվի տեսքը խոշոր պլանով
-
Բելոուսով-Ժաբոտինսկու ռեակցիայի համակարգչային մոդելը
-
Խայտահավի (Numida meleagris) պուտավոր փետուրներ
-
Նիգերի վագրային հորձանքի աերոլուսանկար
-
Նախշեր գետնի վրա, Տակտոյակտուկ, Կանադա
Ծանոթագրություններ[խմբագրել | խմբագրել կոդը]
- ↑ Щекалева М. А. - Бионическая практика Учебно-методическое пособие.
- ↑ Stevens, Peter, 1974, էջ 3
- ↑ Aristotle, 350 до н. э.: «The so-called Pythagoreans, who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things»
- ↑ Singh, Parmanand. Acharya Hemachandra and the (so called) Fibonacci Numbers. Math. Ed. Siwan, 20(1):28-30, 1986. ISSN 0047-6269
- ↑ Knott, Ron. «Fibonacci's Rabbits». University of Surrey Faculty of Engineering and Physical Sciences.
- ↑ About D’Arcy. D' Arcy 150. University of Dundee and the University of St Andrews. Retrieved 16 October 2012.
- ↑ Padovan, 2002, էջեր 305-306
- ↑ Padovan, 2002, էջեր 113-122
- ↑ Zeising, 1854
- ↑ Forbes, Peter. All that useless beauty. The Guardian. Review: Non-fiction. 11 February 2012.
- ↑ Steen, L.A.. The Science of Patterns. Science, 240: 611-616, 1998. Summary at ascd.org Արխիվացված 2010-10-28 Wayback Machine
- ↑ Tatarkiewicz, 1980, էջ 139
- ↑ Poulin, R.; Grutter, A.S. (1996) «Cleaning symbiosis: proximate and adaptive explanations». Bioscience 46(7): 512-517
- ↑ Koning, Ross (1994). «Plant Physiology Information Website». Pollination Adaptations. Ross Koning. Վերցված է 2012 թ․ մայիսի 2-ին.
- ↑ Stewart, 2001, էջեր 64-65
- ↑ Stewart, 2001, էջ 52
- ↑ Stewart, 2001, էջ 71
- ↑ Беклемишев В. Н. Основны сравнительной анатомии беспозвоночных. (в 2-х томах). Т.1. М., «Наука», 1964.
- ↑ Sumrall, Colin D.; Wray, Gregory A. (2007 թ․ հունվար). «Ontogeny in the fossil record: diversification of body plans and the evolution of "aberrant" symmetry in Paleozoic echinoderms». Paleobiology. 33 (1): 149–163. doi:10.1666/06053.1.
- ↑ Mandelbrot, 1982
- ↑ Falconer, 2003
- ↑ Briggs, 1992, էջ 148
- ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. (2005). «Fractal aspects of three-dimensional vascular constructive optimization». In Losa, Gabriele A.; Nonnenmacher, Theo F. (ed.). Fractals in biology and medicine. Springer. էջեր 55–66.
{{cite book}}: CS1 սպաս․ բազմաթիվ անուններ: authors list (link)> - ↑ Rozenberg, Salomaa, 1980
- ↑ Meyer, 1992, էջ 25
- ↑ Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). «Fractal aspects of three-dimensional vascular constructive optimization». In Losa, Gabriele A.; Nonnenmacher, Theo F. (eds.). Fractals in biology and medicine. Springer. էջեր 55–66.
- ↑ Жизнь животных: в 6-ти томах. - М.: Просвещение. Под ред. проф. Н. А. Гладкова, А. В. Михеева. 1970
- ↑ Наталья Московская. Раковины мира. История, коллекционирование, искусство. Издательства: Аквариум-Принт, Харвест, 2007 г. Твёрдый переплет, 256 стр.
- ↑ 29,0 29,1 Kappraff, Jay (2004). «Growth in Plants: A Study in Number» (PDF). Forma. 19: 335–354. Արխիվացված է օրիգինալից (PDF) 2016 թ․ մարտի 4-ին. Վերցված է 2016 թ․ մարտի 23-ին.
- ↑ Ball, 2009, էջ 13
- ↑ Coxeter, 1961, էջ 169
- ↑ Prusinkiewicz, 1990, էջեր 101-107
- ↑ Levitov LS (1991 թ․ մարտի 15). «Energetic Approach to Phyllotaxis» (PDF). Europhys. Lett. 14 (6): 533–9. Bibcode:1991EL.....14..533L. doi:10.1209/0295-5075/14/6/006.
- ↑ Wolfram, 2002
- ↑ von Kármán, Theodore. Aerodynamics. McGraw-Hill (1963): ISBN 978-0070676022. Dover (1994): ISBN 978-0486434858.
- ↑ Lewalle, Jacques (2006). «Flow Separation and Secondary Flow: Section 9.1». Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools (PDF). Syracuse, NY: Syracuse University. Արխիվացված է օրիգինալից (PDF) 2011 թ․ սեպտեմբերի 29-ին. Վերցված է 2016 թ․ մարտի 23-ին..
- ↑ French, A.P. Vibrations and Waves. Nelson Thornes, 1971.
- ↑ Tolman, H.L. (2008), «Practical wind wave modeling», in Mahmood, M.F. (ed.), CBMS Conference Proceedings on Water Waves: Theory and Experiment (PDF), Howard University, USA, 13–18 May 2008: World Scientific Publ.
{{citation}}: CS1 սպաս․ location (link) - ↑ «Types of Dunes». USGS. 1997 թ․ հոկտեմբերի 29. Վերցված է 2012 թ․ մայիսի 2-ին.
- ↑ Strahler, A. & Archibold, O.W. Physical Geography: Science and Systems of the Human Environment. John Wiley, 4th edition 2008. Page 442.
- ↑ Schwämmle, V.; Herrman, H.J. (2003). «Solitary wave behaviour of sand dunes». Nature. 426 (Dec. 11): 619–620 Abstract. Bibcode:2003Natur.426..619S. doi:10.1038/426619a. PMID 14668849.
- ↑ Armstrong, 1988
- ↑ «Giant's Causeway and Causeway Coast». UNESCO World Heritage Centre.
- ↑ «University of Toronto (2008, December 25). Mystery of Hexagonal Column Formations».
- ↑ Stevens, Peter, 1974, էջ 207
- ↑ Stevens, Peter, 1974, էջ 208
- ↑ Darwin, 1859
- ↑ Wickler, 1968
- ↑ «Биологический энциклопедический словарь.» Гл. ред. М. С. Гиляров; Редкол.: А. А. Бабаев, Г. Г. Винберг, Г. А. Заварзин и др. - 2-е изд., исправл. - М.: Сов. Энциклопедия, 1986
- ↑ Smith, S. M. (1975). «Innate Recognition of Coral Snake Pattern by a Possible Avian Predator». Science 187 (4178): 759-760. Bibcode:1975Sci…187..759S. doi:10.1126/science.187.4178.759. PMID 17795249.
- ↑ Ball, 2009, էջեր 159-167
- ↑ Ball, 2009, էջեր 168-180
- ↑ Rothenburg, 2011, էջեր 93-95
- ↑ Prum, 2002, էջեր 781-792
- ↑ 55,0 55,1 Tongway, 2004
- ↑ D'Avanzo, C. (2004 թ․ փետրվարի 22). «Fir Waves: Regeneration in New England Conifer Forests». TIEE. Վերցված է 2012 թ․ մայիսի 26-ին.
- ↑ Morelle, Rebecca. «'Digital gophers' solve Mima mound mystery». BBC News. Վերցված է 2013 թ․ դեկտեմբերի 9-ին.
- ↑ «Permafrost: Patterned Ground». US Army Corps of Engineers. Արխիվացված է օրիգինալից 2015 թ․ մարտի 7-ին. Վերցված է 2015 թ․ փետրվարի 17-ին.
Գրականություն[խմբագրել | խմբագրել կոդը]
- Stevens, Peter Patterns in Nature. — Little Brown and Company, 1974. — 240 с.
- Balaguer Mark Stanford Encyclopedia of Philosophy. — Stanford University, 2009.
- Ian Stewart What Shape is a Snowflake? Magical Numbers in Nature.. — Weidenfeld & Nicolson, 2001. — 224 с.
- Aristotle Metaphysics 1-5. — 350 до н. э..
- Padovan Richard Proportion. — Taylor & Francis, 2002. — ISBN 978-0-419-22780-9.
- Zeising Adolf Neue Lehre van den Proportionen des meschlischen Körpers. — Weigel, 1854. — 457 с.
- Ball Philip 1 Shapes // Nature’s Patterns: a tapestry in three parts. — Oxford, 2009. — 320 с.
- Rozenberg Grzegorz, Salomaa Arto The mathematical theory of L systems. — New York: Academic Press, 1980. — ISBN 0-12-597140-0
- Mandelbrot Benoît B. The fractal geometry of nature. — W. H. Freeman and Company, 1982. — 468 с. — ISBN 978-0716711865
- Devlin, Keith Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe. — Scientific American Library, 1997. — 216 с. — ISBN 978-0716760221
- Darwin Charles On the Origin of Species. — Wordsworth Editions, 1859. — 416 с. — ISBN 978-1853267802
- Wickler W Mimicry in plants and animals. — McGraw-Hill, 1968. — ISBN 978-0070701007
- Falconer Kenneth Fractal Geometry: Mathematical Foundations and Applications. — Wiley, 2003. — 366 с. — ISBN 978-0470848616
- Briggs John Fractals:The Patterns of Chaos. — Simon & Schuster, 1992. — 192 с. — ISBN 978-0671742171
- Batty Michael Fractals – Geometry Between Dimensions. — Holborn Publishing Group, 1985.
- Meyer, Yves Progress in wavelet analysis and applications: proceedings of the International Conference Wavelets and Applications. — Atlantica Séguier Frontières, 1992.
- Carbone Alessandra Pattern formation in biology, vision and dynamics. — World Scientific, 2002. — 444 с. — ISBN 9789810237929
- Addison Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — 256 с. — ISBN 0750304006
- Maor Eli The Story of a Number. — Princeton University Press, 2009.
- Coxeter H. S. M. Introduction to geometry. — Wiley, 1961.
- Prusinkiewicz Przemyslaw The Algorithmic Beauty of Plants. — Springer-Verlag, 1990. — ISBN 9780387972978
- Ruelle David. Chance and Chaos. — Princeton University Press, 1991.
- Stephen Wolfram, A New Kind of Science, «Wolfram Media», 2002։
- French A.P. Vibrations and Waves. — Nelson Thornes, 1971. — 198 с.
- Strahler A., Archibold O.W. Physical Geography: Science and Systems of the Human Environment. — 4. — John Wiley, 2008. — ISBN 978-1-118-08565-3
- Armstrong M.A. Groups and Symmetry. — New York: Springer-Verlag, 1988. — 187 с. — ISBN 978-0387966755
- Hook J.R., Hall H.E. Solid State Physics. — John Wiley & Sons, 2010. — ISBN 978-0-471-92804-1
- Rothenburg David Survival of the Beautiful: Art, Science and Evolution. — Bloomsbury Press, 2011. — 320 с.
- Prum Richard O. Reaction–diffusion models of within-feather pigmentation patterning. — Proceedings Royal Society London, 2002.
- Tongway D.J. Banded vegetation patterning in arid and semiarid environments. — New York: Springer-Verlag, 2001. — 258 с. — ISBN 978-1-412-6559-7
«Պիոներ» հեղինակներ[խմբագրել | խմբագրել կոդը]
- Fibonacci. Liber Abaci, 1202. (լատիներեն)
- Sigler, Laurence E. Fibonacci’s Liber Abaci. Springer, 2002. (անգլերեն)
- Ernst Haeckel Kunstformen der Natur (Art Forms in Nature), 1899-1904.
- D’Arcy Wentworth Thompson. On Growth and Form. Cambridge, 1917.
Հիմնական գրքեր[խմբագրել | խմբագրել կոդը]
- Adam, John A. Mathematics in Nature: Modeling Patterns in the Natural World. Princeton University Press, 2006.
- Philip Ball. Nature’s Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches. Oxford, 2009.
- Pat Murphy and Neill William. By Nature’s Design. Chronicle Books, 1993.
- Rothenburg David. Survival of the Beautiful: Art, Science and Evolution. Bloomsbury Press, 2011.
- Stevens, Peter S. Patterns in Nature. Little, Brown & Co, 1974.
- Ian Stewart. What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson, 2001.
Բնության օրինաչափություններ (որպես արվեստ)[խմբագրել | խմբագրել կոդը]
- Edmaier, Bernard. Patterns of the Earth. Phaidon Press, 2007.
- Macnab, Maggie. Design by Nature: Using Universal Forms and Principles in Design. New Riders, 2012.
- Nakamura, Shigeki. Pattern Sourcebook: 250 Patterns Inspired by Nature.. Books 1 and 2. Rockport, 2009.
- O’Neill, Polly. Surfaces and Textures: A Visual Sourcebook. Black, 2008.
- Porter Eliot и James Gleick. Nature’s Chaos. Viking Penguin, 1990.
Արտաքին հղումներ[խմբագրել | խմբագրել կոդը]
- Ֆիբոնաչիի թվերը և ոսկե հատումը
- Բույսի ձևափոխությունների ուսումնասիրությունների մասին մաթեմատիկան հետազոտությունների ինտերակտիվ կայք Արխիվացված 2012-05-07 Wayback Machine
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի օրվա հոդված: |